Svar på opgave 1: 9. A sælger kaffe
- Eleverne skal betale Idas far: 100 kr. - 3·6 kr. - 2·10 kr. = 100 kr. - 38 kr. = 62 kr.
-
Literprisen for kaffe i små bægre er 6 kr./1,5 dL = 6 kr./[1,5·(1/10) L] = (6/1,5)·10 kr./L = 40 kr./L.
Literprisen for et stort bæger kaffe er 10 kr./2,5 dL = (10/2,5)·10 kr./L = 40 kr./L.
Dermed er literprisen den samme for de to størrelser af bægre. -
Antallet af store bægre kaldes x. Rumfanget af kaffe i store bægre er x·2,5 dL.
Rumfanget af kaffe i små bægre er 80·1,5 dL = 120 dL
Rumfanget af kaffe i små og store bægre skal være lig hinanden: x·2,5 dL = 120 dL ⇒ x = 120/2,5 = 48 -
Antallet af store bægre kaldes x, hvilket giver, at antallet af små bægre er 2·x.
Den samlede indtjening er: 2·x·6 kr. + x·10 kr. = x·12 kr. + x·10 kr. = x·22 kr.
Dette skal give 4400 kr., og man får derfor følgende ligning for x: x·22 kr. = 4400 kr. ⇒ x = 4400/22 = 200.
Dette giver, at antal små bægre = 2·200 = 400 og antal store bægre = 200
Svar på opgave 2: 9. A bygger en skaterrampe
- Sidestykkerne er trapezer. Ende- og topstykket er rektangler.
-
Tegning af udskæringer:
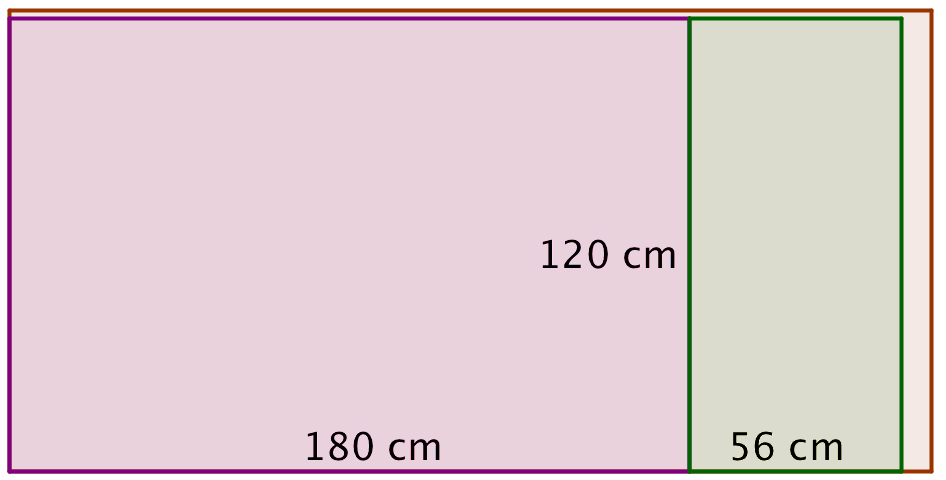
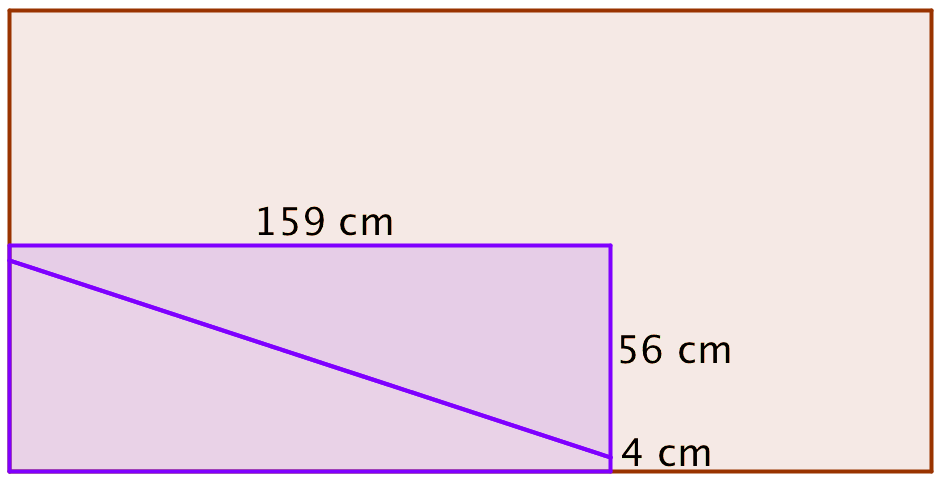
- Rampens længde er katete i en retvinklet trekant, hvor den anden katete er 56 cm og hypotenusen er 180 cm. Skaterrampens længde kaldes x og beregnes ved hjælp af Pythagoras' læresætning: 562 + x2 = 1802 ⇒ x = √[1802 - 562] = 171,1 Det vil sige, at rampens længde er 171 cm
-
Man laver nedenstående tegning i Geogebra og måler vinklen: Det vil sige, at Ali har ret, da vinjlen er mindre end 20°

Svar på opgave 3: 9. A planlægger en turnering
- Der bliver 7 kampe med Frederikkes forslag: 4 i første runde + 2 i anden runde + 1 i tredje runde.
- Der bliver 28 kampe med Najas forslag: Hold ét skal møde 7 andre hold og er derefter færdige. Hold to har mødt hold ét (den kamp er talt) og mangler 6 kampe. Tilsvarende mangler hold tre 5 kampe, hold fire 4 kampe,...og hold syv 1 kamp. I alt: 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28.
- Der er 7 hold tilbage i posen, hvoraf 3 er syvende-klasser. Dette giver sandsynligheden : 3/7 = 43 % for at trække en syvende-klasse.
Svar på opgave 4: 9. A sælger kalendere
- Overskud: 600·15 kr. = 9000 kr.
- Overskud: 375·20 kr. + (600 - 375)·20 kr. = 3000 kr.
- Antal kalendere kaldes x. Af tabellen ses, at hver gang man sælger yderligere 50 kalendere, så stiger indtjeningen med 2000kr., det vil sige med 40 kr. pr. kalender. Sammenhængen er derfor y = 40·x + b, hvor b er indtjeningen for 0 solgte kalendere. Denne findes som: -10.000 kr. - 2000 kr. = -12.000 kr. Dermed er formlen: y = 40·x - 12.000 kr.
- For mulighed 1 er indtjeningen y = x·15 kr., hvor x er antallet af solgte kalendere. Man skal finde det x, hvor de to indtjeninger er ens: 40·x - 12.000 kr. = x·15 kr. ⇔ x = 12.000/(40 - 15) stk. ⇔ x = 480 stk. De skal dermed sælge mere end 480 kalendere for at mulighed 2 skal give større fortjeneste end mulighed 1.
- Man sætter antal indkøbte kalendere lig med y og antal solgte lig med x. Fortjenesten ved mulighed 2 er: (x·20 - (y - x)·20) kr. = 20·(2·x - y) kr. Det vil sige, at de har overskud, hvis x > 0,5·y, hvilket svarer til at sælge mere end halvdelen af kalenderne, og Clara har derfor ret.
Svar på opgave 5: Regneopskrifter
-
Man ender med:
((3 + 10)·3 - 3)/2 - 15 =
(13·3 - 3)/2 - 15 =
36/2 - 15 =
3 -
Tallet man vælger kaldes x. Forskriften er
(((x + 10)·3) - x)/2 - 15 =
(2·x + 30)/2 - 15 =
x + 15 - 15 =
x.
Det vil sige, at resultatet af beregningen er det samme, som tallet man starter med. - Antons og Runes regneudtryk kan reduceres til n, det kan de andre ikke. Det vil sige, at Miriam og Haiders er forkerte.
- Regnestykkes omskrives til: (m·6)/3 - m + 10 = m·2 - m + 10 = m + 10. Dette viser at tal, som man ender med er 10 større end m.
-
Opskrift:
1. Vælg et tal
2. Gang med 6
3. Divider med 3
4. Træk det tal, du valgte i linje 1, fra
5. Læg 10 til
Svar på opgave 6: Romber
- Omkredsen er 4·5 = 20
-
Tegnet i Geogebra:
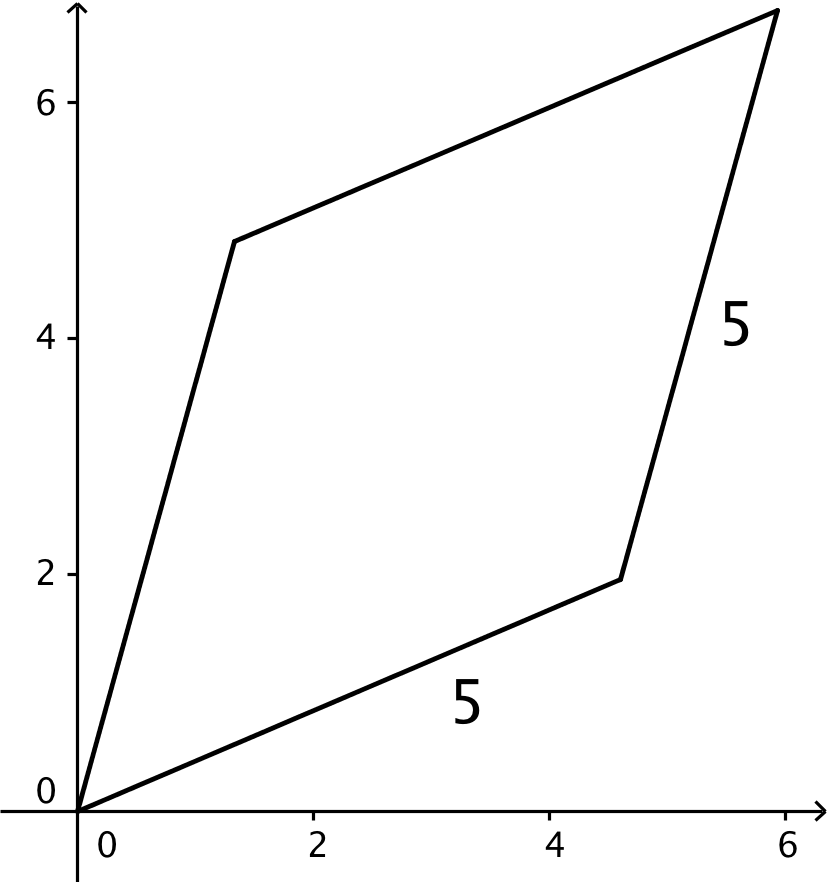
- Det største areal er 25. Dette optræder, når romben er et kvadrat med siden 5. Se Geogebra
- De er ligebenede, fordi de deler sider med romben, hvor alle sider er lige lange og de er kongruente, fordi de også deler diagonalen.
-
Den anden påstand er forkert og modbevises ved et eksempel: