Svar på opgave 1: På tryk - tryk på

1. Frikvarter udkom første gang i 2011 - 17 = 1994
2. Man skal finde antallet af læsere pr. eksemplar. Dette er: (antal læsere)/(antal eksemplarer) = (108.000 læsere)/(70.000 eksemplarer) = 1,54 læsere pr. eksemplar af bladet.
3. Andelen af sider i bladet, som er reklamer, er 24 ud af 54, der er lig med 24/54 = 0,444 = 44 %
4. Forskellen på deres tider er 22,09 s - 19,78 s = 2,31 s. Det vil sige, at Anilla var 2,31 sekunder hurtigere end Wiswus.
5. En normalside er 2400 ord. Anilla taster 160 ord på 19,78 sekunder. Dette svarer til (19,78 s)/(160 ord) = 0,1236 s/ord. For 2400 ord giver det tiden:
   (2400 ord)·(0,1236 sekunder/ord) =
   296,64 sekunder =
   (296,64/60) minutter =
   4,944 minutter =
   4 minutter + (0,944·60) sekunder =
   4 minutter og 57 sekunder
   Det vil sige, at Anilla bruger 4 minutter og 57 sekunder på at taste en normalside.

Svar på opgave 2: På DVD

1. Prisen pr. dvd er (57,98 kr.)/(50 stk.) = 1,160 kr./dvd
2. Prisen i Euro er (7,48 €/(50 dvd'er))·(758,43 kr./100 €) = 56,7306 kr./(50 dvd'er) Prisforskellen er: (57,98 - 56,73) kr. = 1,25 kr.
3. Pris uden moms kaldes x. For den danske pris uden moms får man:
   x + x·25 % = 57,98 kr. ⇔
   x·(1 + 25 %) = 57,98 kr. ⇔
   x·1,25 = 57,98 kr. ⇔
   x = 57,98 kr./1,25 ⇔
   x = 46,38 kr.
   For prisen i Tyskland uden moms får man
   x = 56,7306 kr./1,19 = 47,67 kr.
   Uden moms er prisen højere i Tyskland. Prisforskellen er: (47,67 - 46,38) kr. = 1,29 kr.
4. Man omregner først alt til samme enhed. 4,7 GB = 4700 MB. Dernæst dividerer man størrelsen af et nummer i MB op i den samlede plads i hukommelsen på en dvd. Dette giver: (4700 MB/dvd)/(35 MB/nummer) = 134,29 numre/dvd. Det vil sige, at der kan højst være ca. 134 musiknumre pr. dvd.
5. Man vælger en pakke der har to cylindre på hver led: længde, bredde og højde. Denne pakke har dimensionerne: Højde: 2·9,5 cm = 19,0 cm, længde: 2·12,4 cm = 24,8 cm og bredde: 2·12,4 cm = 24,8 cm
6. Man går ud fra, at pakkerne består af to lag med fire cylindere i hver.
   I længden kan der være: (60 cm)/(24,8 cm/pakke) = 2,42 pakker ≈ 2 pakker
   I bredden kan der være: (80 cm)/(24,8 cm/pakke) = 3,23 pakker ≈ 3 pakker
   I højden kan der være: (160 cm)/(19,0 cm/pakke) = 8,42 pakker ≈ 8 pakker
   Det vil sige, at når den maksimale højde er 1,6 m, så er det maksimale antal af pakker på pallen: 2·3·8 stk. = 48 stk.
   Vægt af palle plus pakker = 350 kg. Pallen vejer 9,1 kg, og dermed må pakkerne højst veje: 350 kg - 9,1 kg = 340,9 kg. Den samlede vægt pr. pakke er 8·1 kg + 0,25 kg = 8,25 kg.
   Antallet af pakker man kan have uden, at de vejer mere end 340,9 kg er: (340,9 kg)/(8,25 kg/pakke) = 41,32 pakker. Det vil sige, at der kan højst være 41 pakker på pallen, hvis vægtgrænsen og højdegrænsen skal overholdes.
   Antallet af dvd'er er: (41 pakker)·(8 cylindre/pakke)·(50 dvd'er/pakke) = 16.400 dvd'er.
   Det vil sige, at pallen kan højst rumme 16.400 dvd'er

Svar på opgave 3: På TV

1. Længden af diagonalen er (32 tommer)·(2,54 cm/tomme) = 81,3 cm
2. Der gælder at (længste side)/(korteste side) = 16/9. Dermed er den længste side: (27 cm)·(16/9) = 48 cm
3. Forholdet mellem længste og korteste side er 16/9. Man får: Sidelængde = (52,3 cm)·(16/9) = 92,98 cm
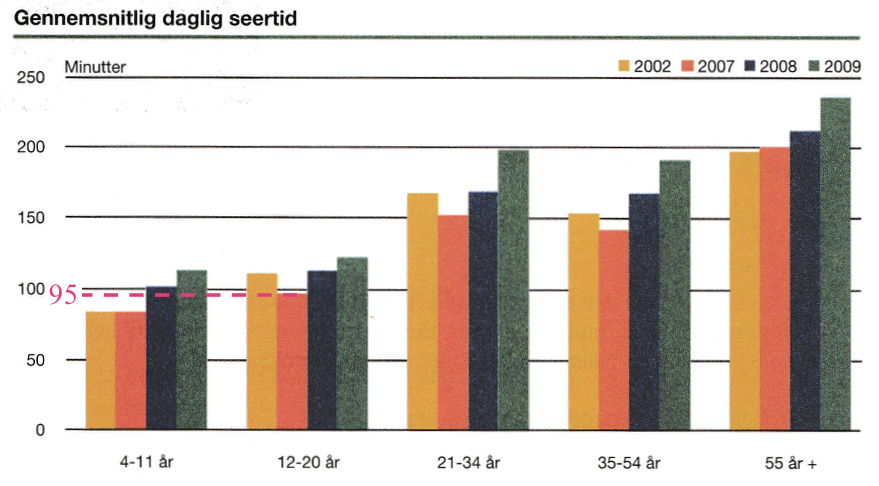
4. Man aflæser som vist nedenunder, at den gennemsnitlige daglige seertid for 15 årige var 95 minutter i 2007.
   
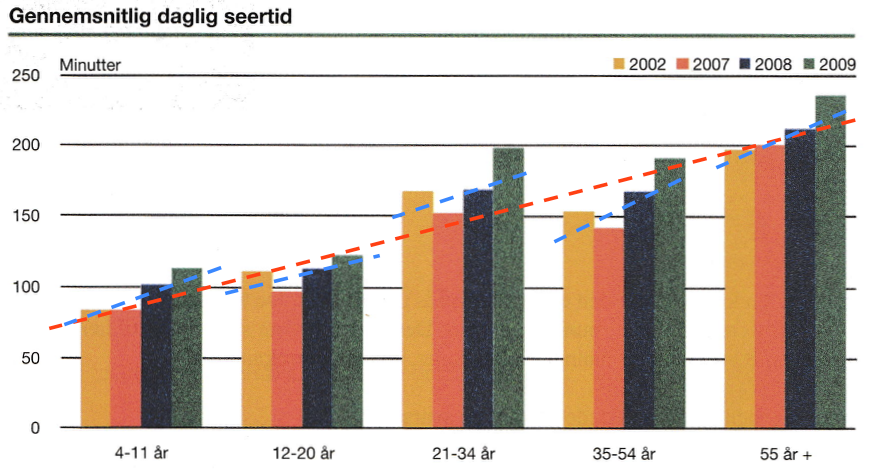
5. På grafen nedenunder er vist to sammenhænge. Den røde linje viser, at der sker en stigning i gennemsnitlig daglig seertid med alderen. Jo ældre man er, jo længere ser man TV om dagen.
   De blå linjer viser, at der sker en stigning fra 2002 til 2009 i seertiden for alle aldersgrupper. Dog sker der en nedgang fra 2002 til 2007 for nogle aldersgrupper.
   
6. Deskriptorerne variationsbredde og kvartilsæt kan samles i boksplot som vist nedenunder.
   
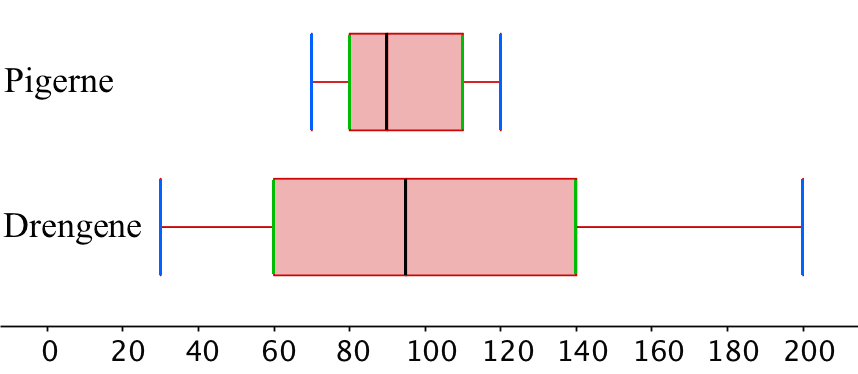
   Variationsbredde. Man ser, at variationsbredden (afstanden mellem de blå linjer i hvert plot) er større hos drengene end hos pigerne. Hos drengene er variationsbredden (200 - 30) minutter/dag = 170 minutter/dag og hos pigerne er den (120 - 70) minutter/dag = 50 minutter/dag.
   Median. Medianen er den sorte streg i hvert boksplot. Den viser hvilken daglig seertid som 50 % af pigerne eller drengene ligger under. For pigerne er medianen 90 og for drengene er den 95.
   Kvartilsæt. Kvartilsættene for piger henholdsvis drenge er de grønne streger og medianen i hvert boksplot. Den første grønne linje til venstre er nedre eller første kvartil, så kommer medianen eller anden kvartil og til sidst kommer den anden grønne linje, som er øvre eller tredje kvartil.
   Nedre kvartil er det antal minutter om dagen som 25 % af pigerne eller drengene ligger under. Øvre kvartil er det antal minutter om dagen, som 75 % af pigerne eller drengene ligger under.
   For pigerne er kvartilsættet: {øvre kvartil, median, øvre kvartil} = {80,90,110} og for drengene er det {øvre kvartil, median, øvre kvartil} = {60,95,140}
   Middeltal. Middeltallet er gennemsnittet af tallene. For pigerne er den (120 + 90 + 90 + 110 + 100 + 80 + 80 + 120 + 70 + 90)/10 minutter/dag = 95 minutter/dag. For drengene er den: (110 + 60 + 180 + 70 + 120 + 90 + 140 + 30 + 60 + 200 + 100 + 40 + 50 + 150)/14 minutter/dag = 100 minutter/dag.
   Typetal. Typetallet er det tal, som der er flest af. For pigerne er det 90 og for drengene er det 60.

Svar på opgave 4: På film

1. Midtpunktet af et rektangel er krydsningspunktet for dets diagonaler. Dette er vist nedenunder.
   
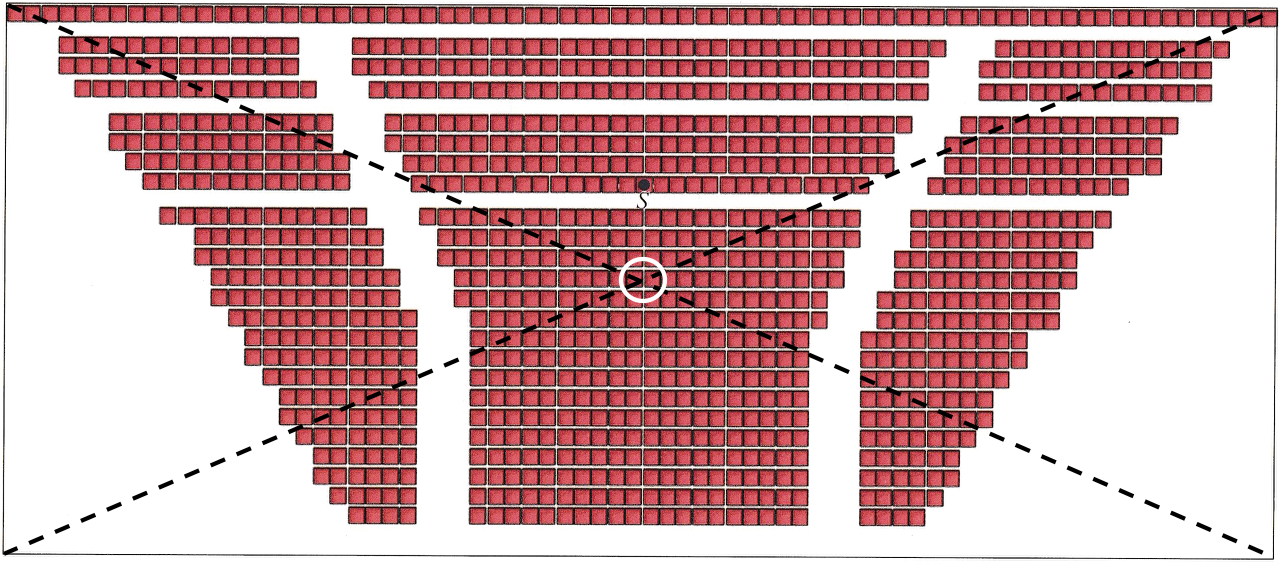
2. Konstruktionen af den retvinklede trekant er vist nedenunder. Når trekanten er ligebenet og retvinklet ved man, at de to sidste vinkler begge er 45°. Dette er brugt til at konstruere trekanten ud fra linjestykket AB.
   
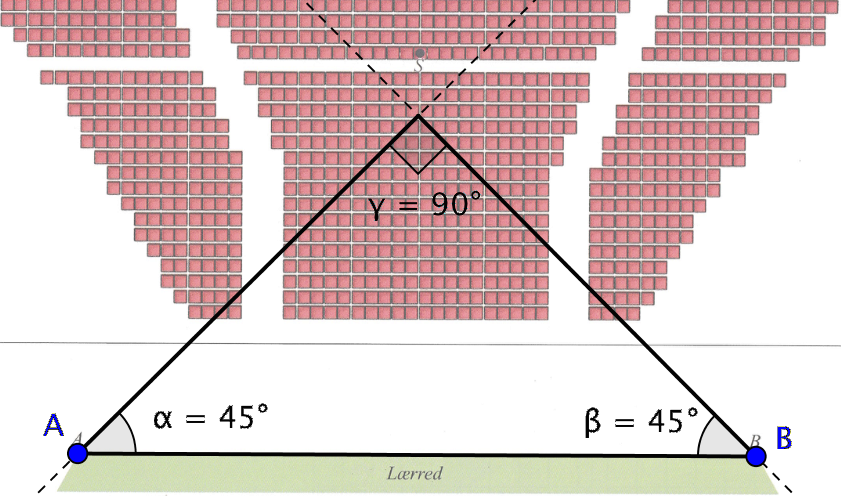
3. På nedenstående figur kaldes højden fra S ned på linjestykket AB for D. Man skal finde |DS| som på tegningen også kaldes h. Man ved, at |BD| = 0,5·|AB| = 0,5·15,6 = 7,8. Man ved også, at vinkel B = 50°, fordi vinkel S = 80, og da trekant ABS er ligebenet gælder, at vinkel A = vinkel B = (180° - 80°)/2 = 50°.
   
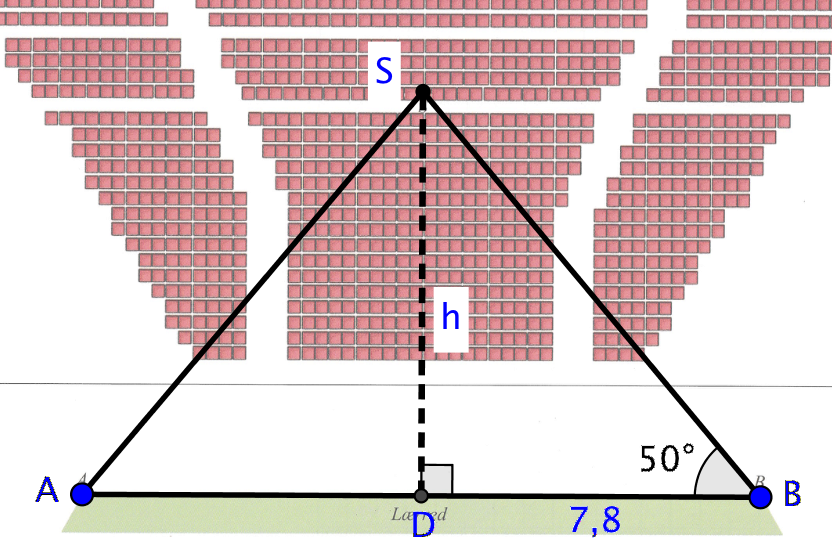
   H kan beregnes ud fra formlen: tan(50°) = h/7,8 ⇒ h = 7,8·tan(50°) = 9,3
4. Lånet koster 600.000 kr. + (600.000 kr.)·2 % + 600 kr. = 600.000 kr. + 12.000 kr. + 600 kr. = 612.600 kr.
5. Nedenfor er vist terminsbergninger i Excel. Man forsætter termin for termin indtil man når til en negativ saldo. Den første termin, der giver en negativ saldo, er lånets løbetid eller antal terminer for lånet.
   
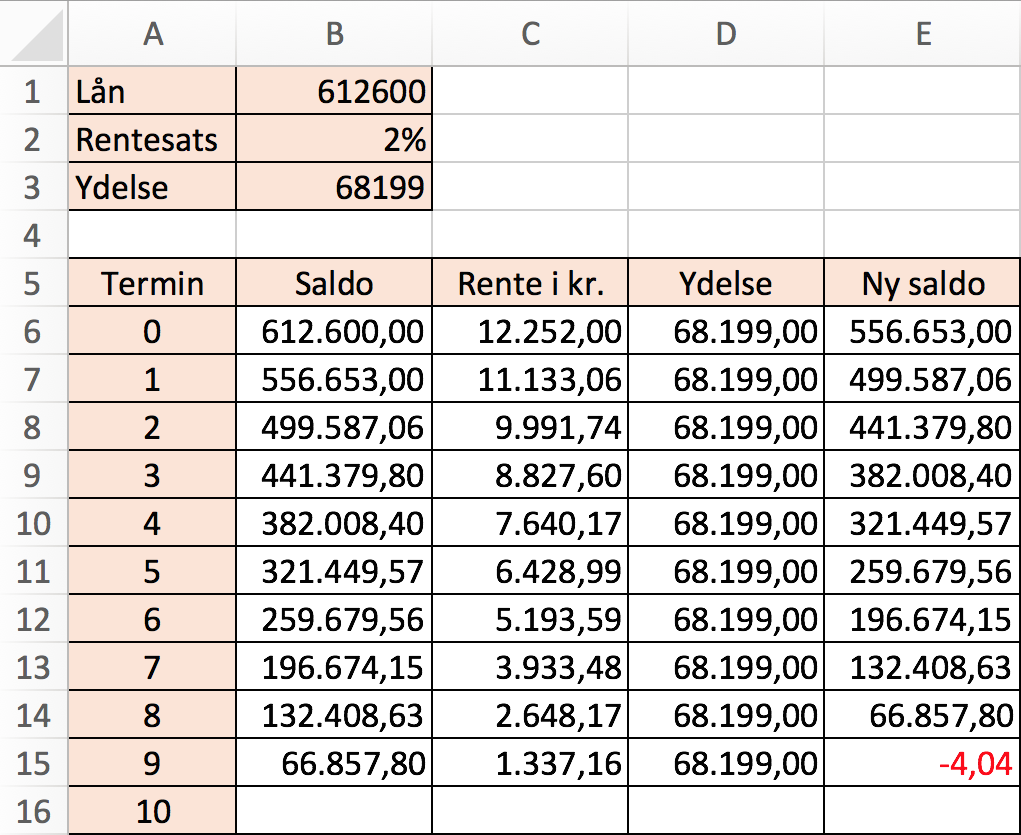
   Antallet af terminer ses at være 9
6. Tallet Φ er med to decimaler: (√5 + 1)/2 = 1,62
7. Nedenfor er billedet inddelt efter det gyldne snit i Geogebra. Billet er sat in så den korte side passer med længden 1 på x-aksen af koordinatsystemet. Et punkt er afsat i x = 0,62 på x-aksen. Dernæst er tegnet to ens cirkler med centrum i hvert sit nedre hjørne af billedet. Radius = 1 - 0,62 = 0,38.
   Dermed er nederste side inddelt efter det gyldne snit, og man opretter nu den vinkelrette i hvert punkt. Dernæst tegnes diagonalerne til rektanglet. Der hvor de skærer de vinkelrette linjer er brændpunkterne for det gylne snit.
   Til sidste tegnes vandrette linjer gennem brændpunkterne, så også de længste sider er índdelt efter det gyldne snit.
   

Svar på opgave 5: I koordinatsystem

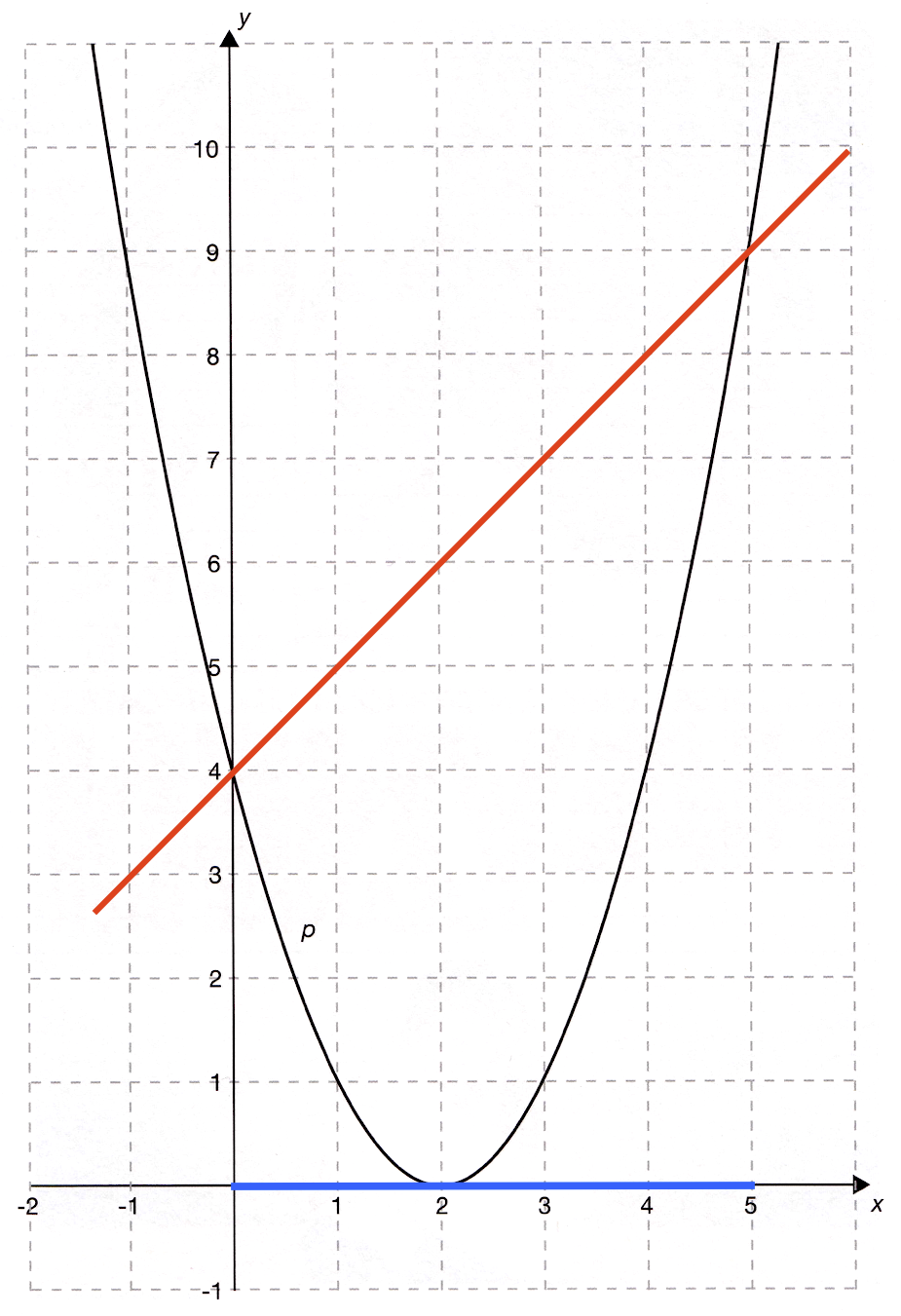
1. Linjen m er vist med rødt på grafen nedenfor.
   
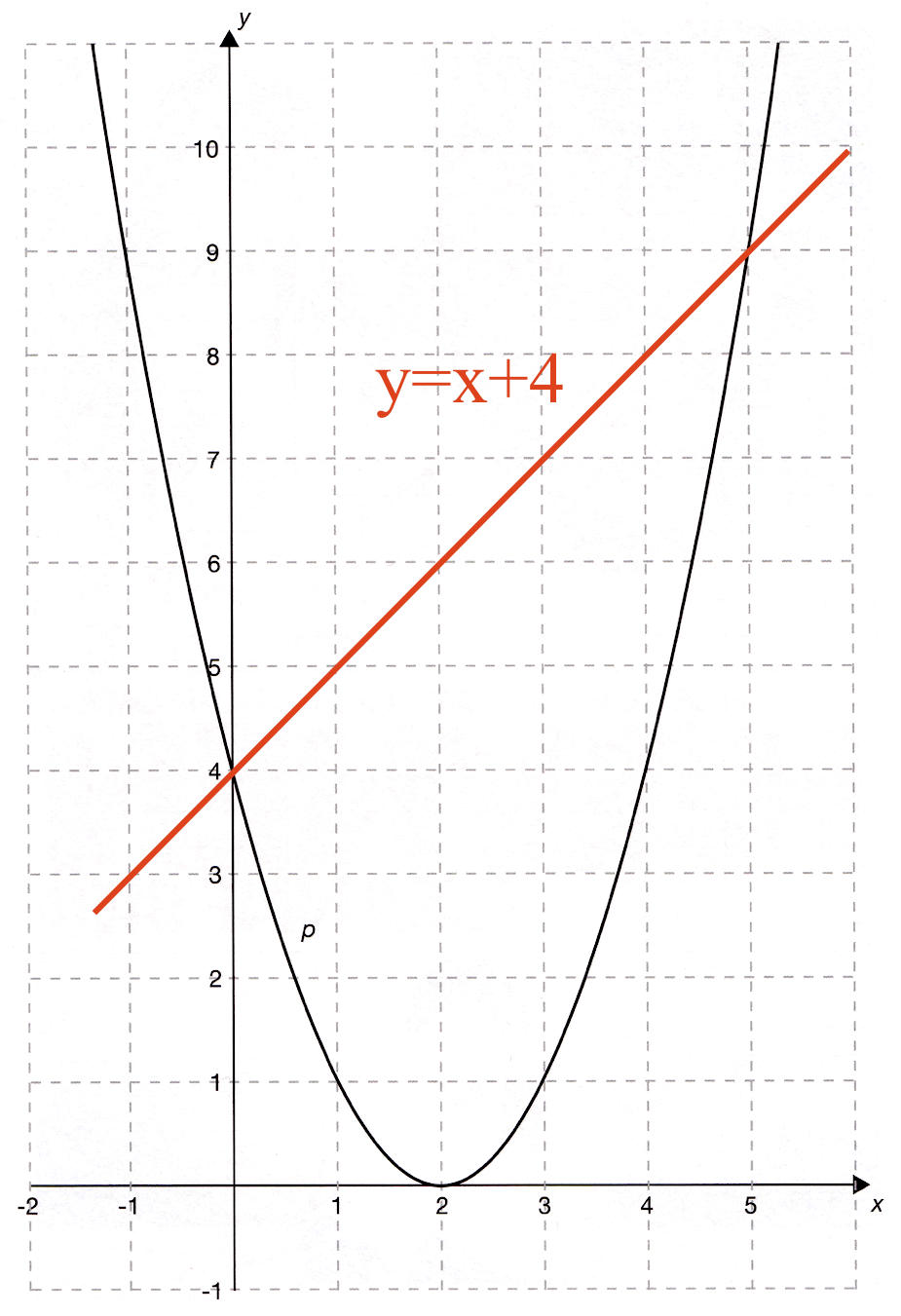
2. Der er en lineær sammenhæng mellem y og x for linjen m. Y er lig med x plus 4.
3. Et punkt i et koordinatsystem kan generelt skrives (x,y). Her er (x,y) = (10,64), dvs. x = 10 og y = 64 for punkt C.
   Hvis punktet ligger på linjen skal der gælde, at y = x + 4, dvs. at 64 = 10 + 4 ⇔ 64 = 14 hvilket er forkert.
   Dermed ligger punktet C ikke på linjen m
   Hvis C ligger på parablen skal der gælde, at y = x² - 4x + 4 ⇒ 64 = 10² - 4·10 + 4 ⇔ 64 = 100 - 40 + 4 ⇔ 64 = 64.
   Da dette er opfyldt, gælder at C ligger på parablen p
4. Man kan beregne x-xærdierne til skæringspunkterne ved hjælp af den andengradsligning, der fremkommer, når man sætter udtrykket p lig med udtrykket for m. Dette giver:
   x² - 4x + 4 = x + 4 ⇔
   1·x² + (-5)·x + 0 = 0 ⇔
   x = -(-5)/2·1±(1/2·1)√[(-5)²-4·1·0] ⇔
   x = 5/2±(1/2)√[25] ⇔
   x = 5/2±5/2 ⇔
   x = 0 ∨ x = 5
   For at finde de tilhørende y-værdier for skæringspunkterne sætter man x-værdierne ind i m's ligning.
   For x = 0 får man y = 0 + 4 = 4 og for x = 5 får man y = 9.
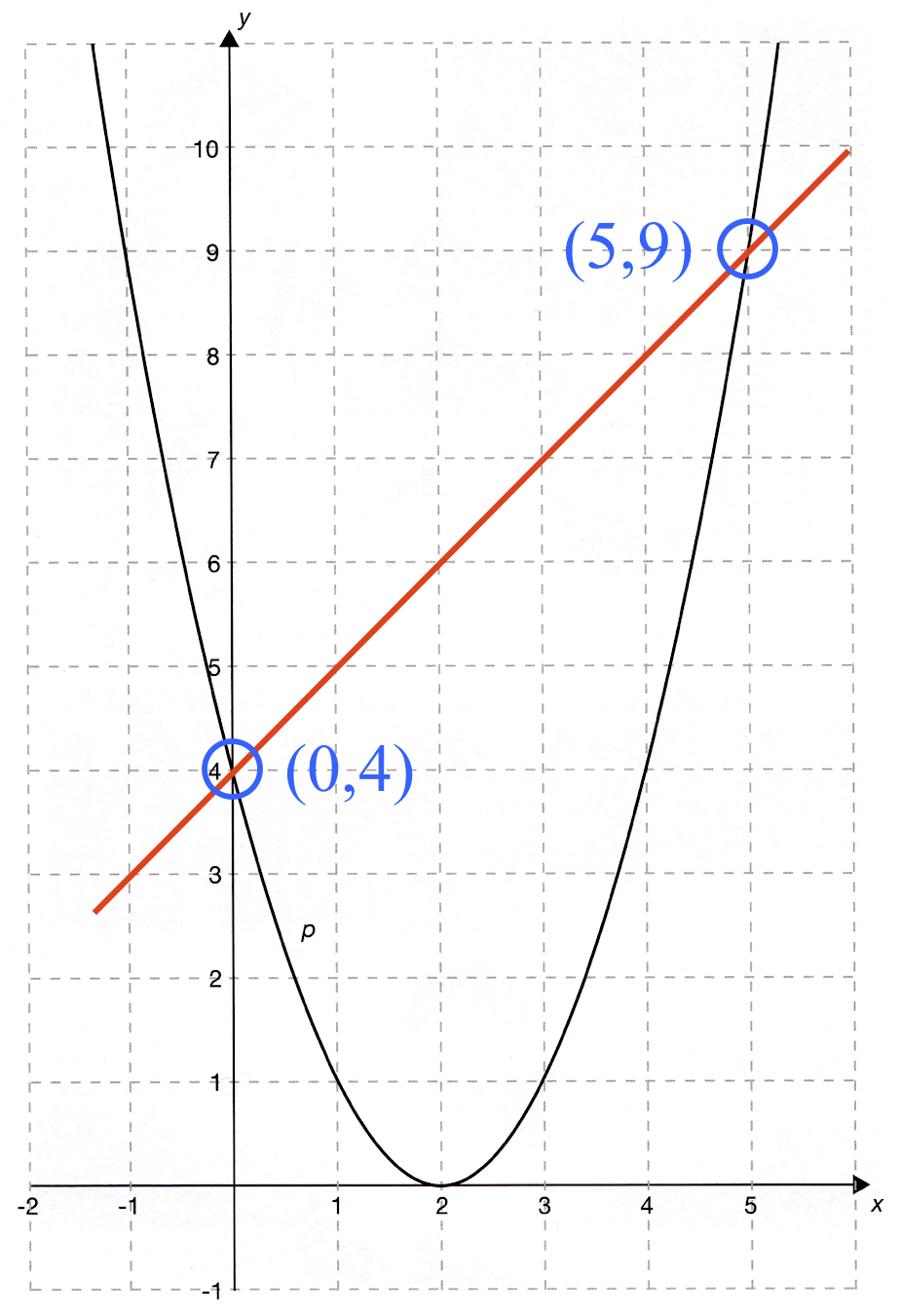
   Det vil sige, at skæringspunkterne er (x,y) = (0,4) eller (x,y) = (5,9)
   På figuren nedenunder er skæringspunkterne markeret med blå ringe.
   
5. Intervallet, hvor parablen p ligger under den rette linje m er intervallet fra x = 0 til x = 5, som vist med blåt på nendenstående figur. Det kan også skrives 0<x<5.