Svar på opgave 1: For lidt eller for meget søvn?

1. Hun sover 30 minutter fra 23.30 til 24.00. Dernæst sover hun 7 timer og 15 minutter fra 24.00 til 07.15.
   I alt sover hun 30 minutter + 7 timer + 15 minutter = 7 timer og 45 minutter
2. I gennemsnit har hun sovet: (5·8 timer + 2·10 timer)/(7 døgn) = (60 timer)/(7 døgn) = 8,57 timer pr. døgn
3. Anbefalingen for 15-årige er 8-9 timers søvn pr. døgn. I 9. klasse er der 8 + 9 + 5 + 3 + 2 + 3 = 30, der overholder anbefalingerne. Der er i alt 25 + 20 = 45 elever i 9. klasse. Procentdelen af elever, der overholder anbefalingerne er derfor: (30/45)·100% = 67 %
4. Nedenfor er vist et boksplot for hver af de to klasser, som er tegnet i Geogebra.
   
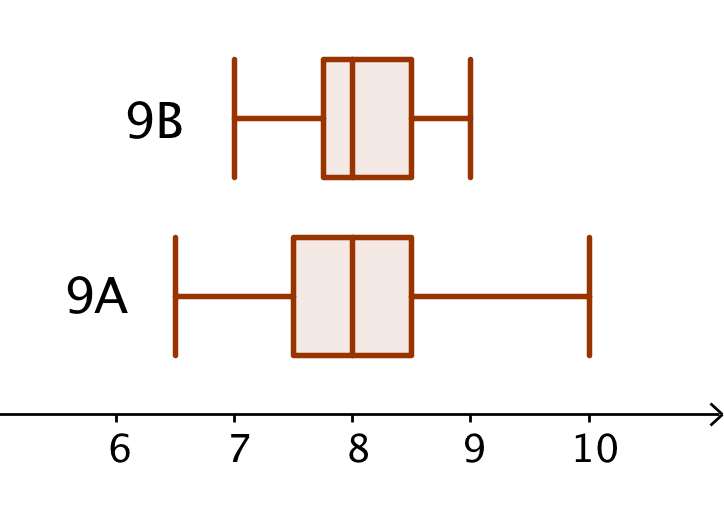
5. Ligheder mellem de to klasser: samme typetal (den værdi der optræder flest gang, nemlig 8 timer), samme median (8 timer) og samme middeltal (det er ikke vist på boksplottet)
   Middeltallet kan beregnes ved at lægge alle timer sammen for alle elever og dividere med antal elever i den enkelte klasse. Man får for 9A: (1·6,5+4·7,0+3·7,5+8·8,0+5·8,5+2·9,0+1·9,5+1·10,0)/25 = 8,04. For 9B får man 8,05.
   Forskelle: Variatonsbredde (forskel mellem største og mindste værdi for søvn i en klasse) og en større del af 9B følger reglerne.

Svar på opgave 2: Til sundhedsplejerske

1. Den letteste elev vejer 42,2 kg og den tungeste vejer 85 kg. Forskellen er (85 - 42,2) kg = 42,8 kg
2. Man finder antal kg fedt for elev nummer 1 ved at gange vedkommendes vægt og fedtprocent med hinanden. Man får: (55,7 kg)·6,1 % = 55,7·0,061 kg = 3,4 kg
3. Elev nummer 14 vejer 51 kg og er 1,71 meter høj. BMI = 51/(1,71·1,71) = 17,44
4. BMI = m/h²
5. Man tæller alle elever, der har et BMI mellem 18,5 og 25 (begge tal inklusive), og får at der er 12
6. Elev nummer 15 vejer 76,4 kg og har højden 1,71 m. Det antal kg, som elev nr. 15 skal tabe, kaldes x. Dette tal findes af følgende ligning:
   BMI = (76,4 - x)/(1,71²) = 24 ⇒
   76,4 - x = 24·1,71² ⇒
   x = -24·1,71² + 76,4 ⇒
   x = 6,2
   Dette viser, at elev nr. 15 skal tabe 6,2 kg for at få et BMI på 24.

Svar på opgave 3: Erobre flaget

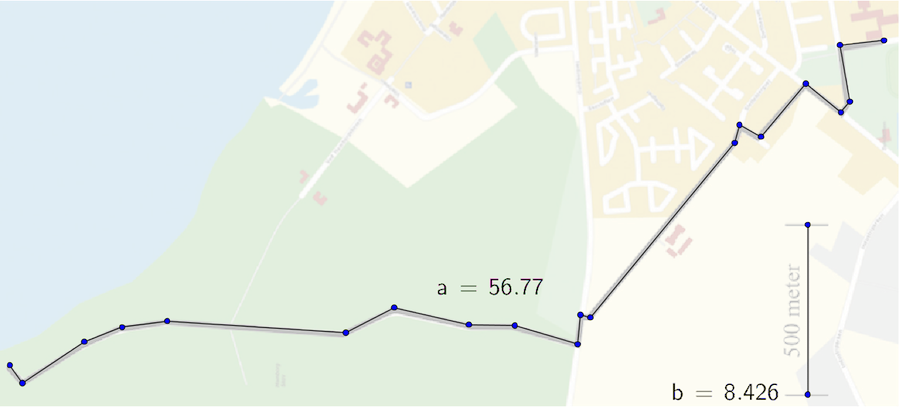
1. Afstanden er målt i Geogebra på nedenstående figur. Turen og målestokken er målt til henholdsvis 56,8 enheder og 8,4 enheder. Det vil sige, at 500 meter går 56,8/8,4 = 6,76 gange op i turens længde. Turen er derfor: 6,76·500 meter = 3381 meter = 3,4 km
   
2. Et muligt eksempel på en løsning er vist herunder lavet i Geogebra.
   
3. Ved hjælp af trigonometri får man: tan(21°) = a/(334 m) ⇒ a = (334 m)·tan(21°) = (334 m)·0,38386 = 128,2 m
4. Arealet af den retvinklede trekant er lig med en halv gange katete 1 gange katete 2 = 0,5·(334 m)·(128 m) = 21.409 m²
5. AC er hypotenusen i en retvinklet trekant, hvor kateterne har længderne 128 m og 334 m. Hypotenusens længde bliver i følge Pythagoras læresætning: √(128² + 334²) m = 358 m
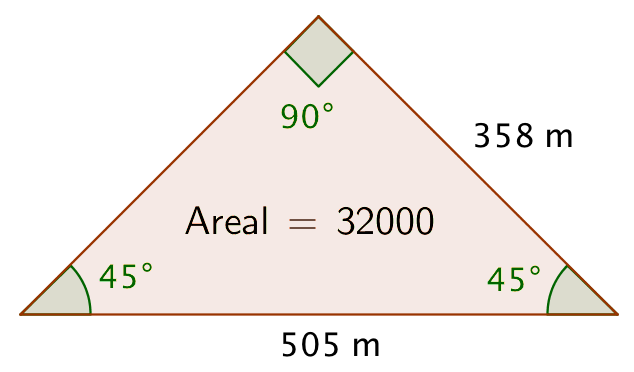
6. Der er mange løsninger, f.eks.: en ligebenet retvinklet trekant med topvinklen 90° og grundvinklerne 45°; sidelængde = 358 m og grundlinje 505 m.
   

Svar på opgave 4: På efterskole

1. Den årlige pris er antal uger gange pris pr. uge, dette giver den samlede pris: 41·1830 kr. = 75.030 kr.
2. Lines egenbetaling for et år er (75.030 - 31.488) kr. = 43.542 kr.
3. Lines egenbetaling er 43.542 kr. og familiens indkomstgrundlag er 560.000 kr. Forholdet mellem egenbetaling og indkomstgrundlag for Line er (100 %)·(43.542 kr.)/(560.000 kr.) = 7,8 %
   Annes egenbetaling er = (75.030 - 20.910) kr. = 54.120 kr. Hendes families indkomstgrundlag er 1.000.000 kr. Forholdet mellem egenbetaling og indkomstgrundlag for Anne er: (100 %)·(54.120 kr.)/(1.000.000 kr.) = 5,4 %
4. Det udfyldte ark med udgifter er vist nedenunder.
   
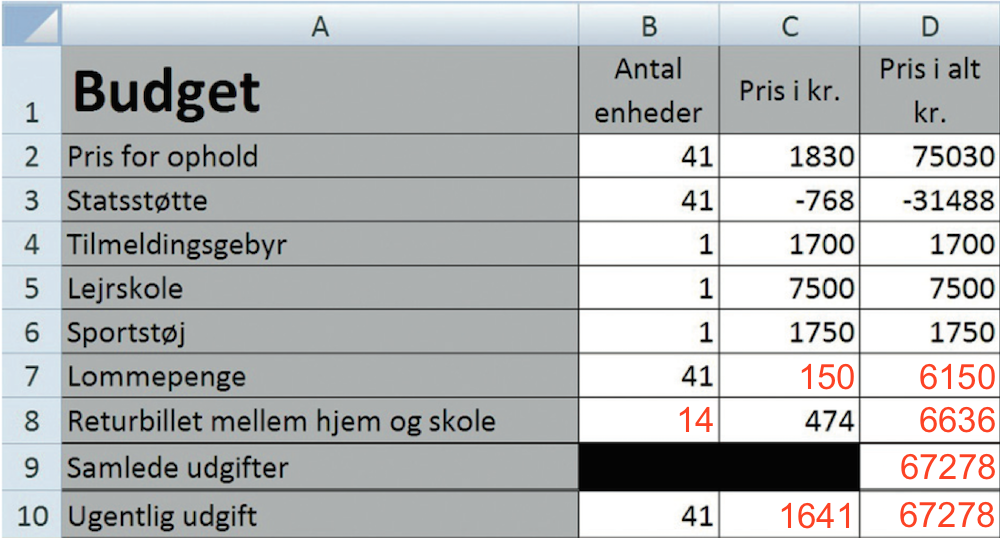
5. Line skal spare (1641 - 1500) kr. = 141 kr. om ugen eller i alt 5781 kr. Dette er ca. 50% af hendes udgifter til rejser og lommepenge, så hun kan evt. sætte antallet af rejser ned til 7 og lommepenge ned til ca. 75 kr. pr. uge.

Svar på opgave 5: Sammenhænge i kvadrater

1. Omkredsen af et kvadrat med sidelængden 2,5 cm aflæses til 10 cm som vist på nedenstående billede.
   
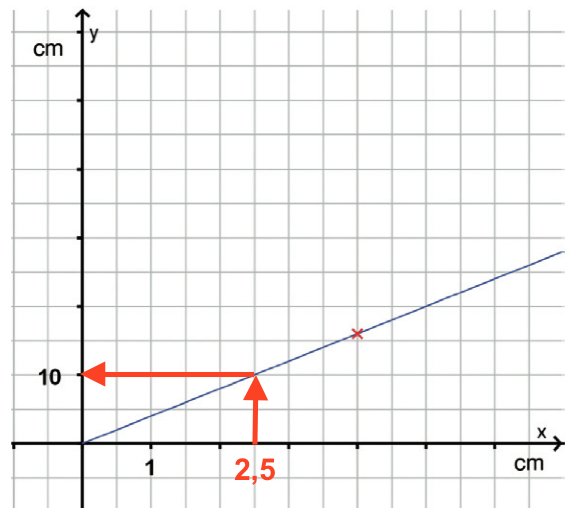
2. Punktet (4,16) på grafen viser, at et kvadrat med sidelængden 4 cm har en omkreds på 16 cm.
3. I et kvadrat er omkredsen fire gange sidelængden. Dette kan skrive y = 4x (x > 0), hvor y er omkredsen målt i cm og er sidelængden målt i cm.
4. Skema med sammenhængende værdier af længde x og bredde y for et rektangel med areal 16 cm².
   
5. Der gælder at x·y = 16, det vil sige, at y = 16/x, hvor x er større end 0.