Svar på opgave 1: Bermudatrekanten

1. Nedenunder er trekanten tegnet ind på kortet.
   
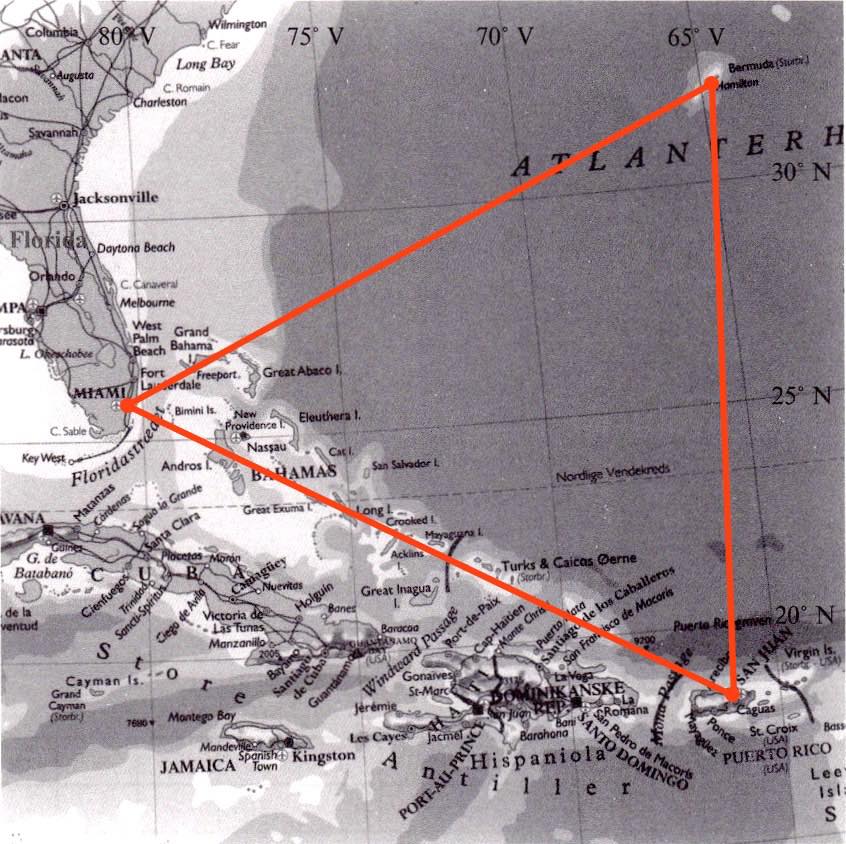
2. Nedenunder er lavet en opmåling i Geogebra. Der er tegnet et linjestykke mellem Hamilton og San Juan, som er målt til 4,086 enheder. Målestokken er målt til 1,575 af de samme enheder.
   
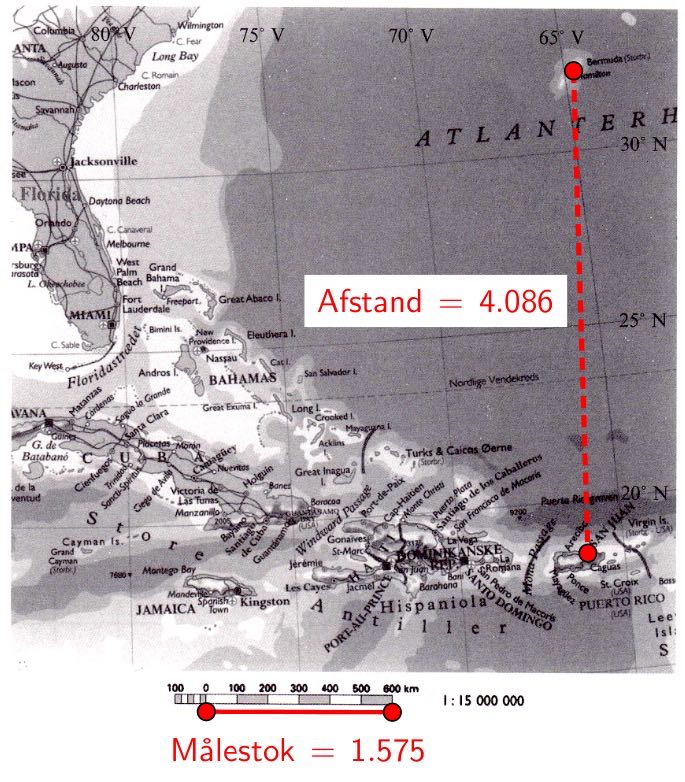
   Målestokken svarer til 600 km i virkeligheden. Dermed er en enhed i Geogebras koordinatsystem lig med (600 km)/(1,575 enheder) = 380,95 km/enhed. Afstanden mellem Hamilton og San Juan er derfor: (4,086 enheder)·(380,95 km/enhed) = 1557 km = 1560 km
3. Siden på et kvadrat, der har arealet 44.000 km² er kvadratroden af 44.000 km².
   Det vil sige, at kvadratets sidelængde er √[44.000 km²] = √[44.000] km = 209,8 km
4. På tegningen i Geogebra har man, at 1 enhed = 380,95 km, og dermed at 1 km = (1 enhed)/380,95 = 0,002625 enheder. 209,8 km svarer dermed til 209,8·(0,002625 enheder) = 0,5507 enhder. Kvadratet er indtegnet med grøn farve på kortet nedenunder i Geogebra.
   

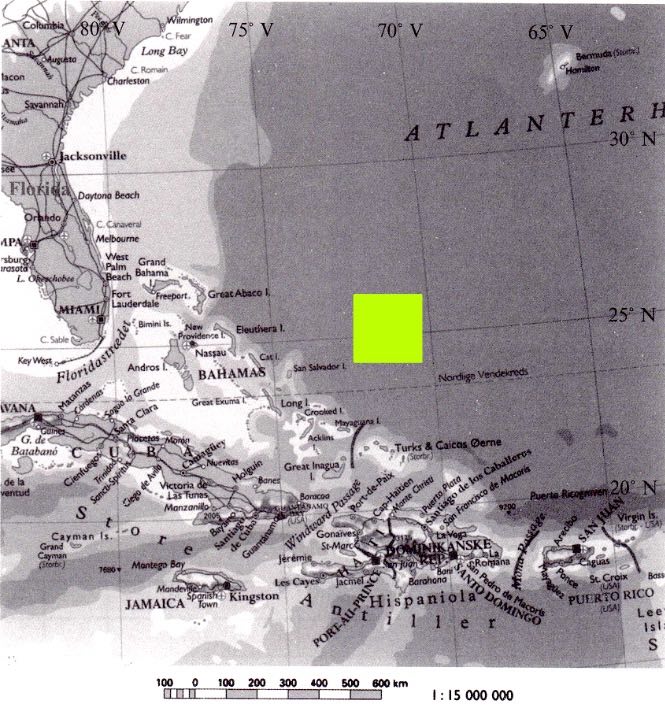
Svar på opgave 2: Cestius pyramide

1. Pyramidens alder er (2008 + 18) år = 2026 år
2. 125 fod = 125·(1 fod) = 125·(29,4 cm) = 125·29,4 (cm) = 125·29,4·(0,01 m) = 125·29,4·0,01 m = 36,75 m
3. Thomas er 1,80 m. Forholdet mellem hans og pyramidens højde er (36,75 m)/(1,80 m) = 36,75/1,80 = 20,4
4. Pyramidens rumfang er (1/3)·højde·grundflade = (1/3)·(125 fod)·(100 fod)² =
   (1/3)·125·100² fod³ = (1/3)·125·10000 fod³ =
   (1/3)·125·10000·(0,294 m)³ =
   (1/3)·125·10000·0,294³ m³ = 10.588,4 m³

Svar på opgave 3: Opdeling i trekanter

1. Jordstykkets areal = areal af trekant 1 + areal af trekant 2 = (0,5·42,1·16 m²) + 80,2 m² = 417 m²
2. Man undersøger om trekant 2 er retvinklet ved at bruge Pythagoras læresætning. Hvis trekant 2 er retvinlet, så skal der gælde, at den længste side i anden er lig med summen af hver af de korte sider i anden. Man får:
   Summen af kvadraterne på de korte sider: 6,12² + 45,0² = 2062,45
   Kvadratet på den længste side: 50,2² = 2520,04
   Da de to tal er forskellige, så er trekant 2 ikke retvinklet
3. Han skal betale følgende i leje for jordstykket om året: areal af jordstykke i kvadratmeter gange årlig leje i kr. pr. kvadratmeter = 417 m²·(0,25 kr./m²) = 104,25 kr./år
4. Arealet af den del af jordstykket, hvor han dyrker kartofler, er: (417 m²)·35 % = 417·0,35 m² = 145,95 m²
5. Antallet af kilogram kartofler er udbyttet pr. hektar gange antallet af hektar. En hektar er 10.000 m².
   Udbyttet i kilogram er (145,95 m²)·(38 ton/hektar) =
   (145,95 m²)·(38 ton/(10.000 m²)) =
   (145,95·38/10.000) tons =
   [145,95·38/10.000]·(1000 kg) =
   554,6 kg
6. En familie på 5 personer spiser 5 gange 60 kg kartofler = 5·60 kg = 300 kg. Dvs. udbyttet af kartofler på ca. 555 kg er stort nok til at dække familiens årlige behov.

Svar på opgave 4: Trekantstal

1. Nedenfor er kegle 8 og 9 tegnet ind som røde prikker på linjen i Geogebra.
   
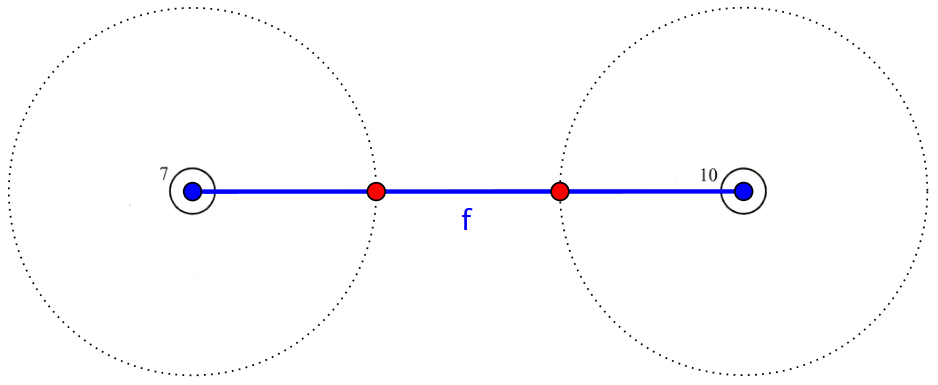
   Man starter med at lave et linjestykke ud fra de to givne punkter. Linjestykket er her blåt og kaldes f.
   Man skal dele linjestykket i tre lige store dele og klikker derfor på hvert af yderpunkterne og vælger cirkel-med-radius værktøjet. Her skriver man "f/3" som radius, hvilket betyder, at Geogebra opretter en cirkel med en radius, der er en tredjedel af linjestykkets længde.
   Keglernes placering er cirklernes skæringer med linjestykket.
2. Nedenfor trekanten konstrueret i Geogebra.
   
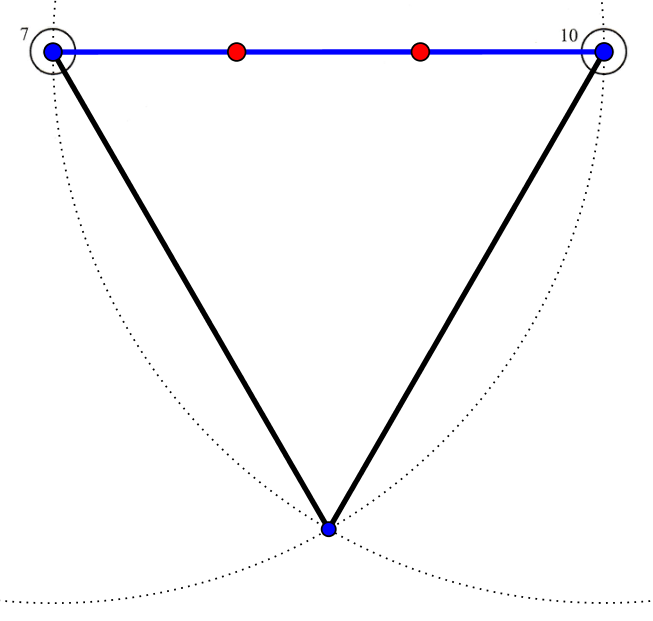
   Man tegner en cirkel i kegle 7 og 10 med linjestykket mellem dem som radius. Cirklernes ene skæringspunkt er kegle 1 (her det nederste hjørne i trekanten).
3. Nedenfor de sidste kegler indsat i trekanten i Geogebra.
   
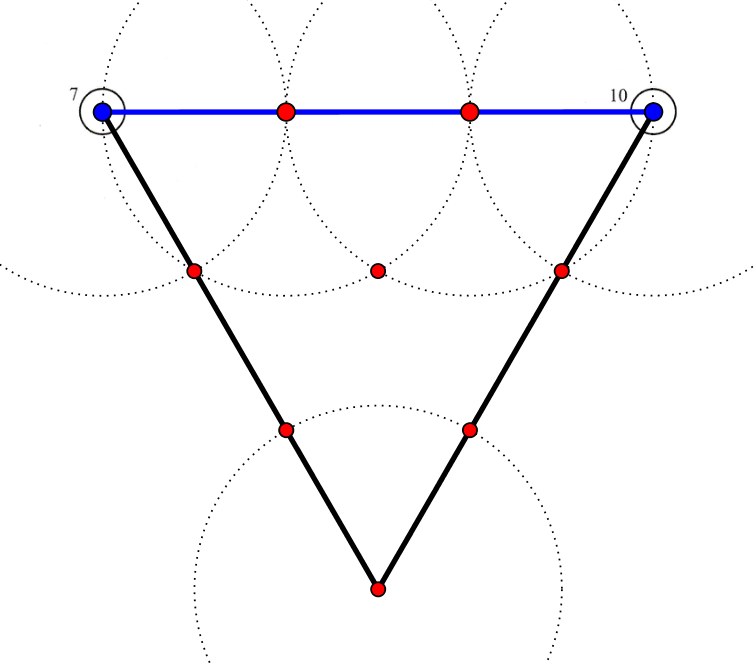
   Man tegner små cirkler som før og benytter deres skæringspunkter indbyrdes og deres skæringspunkter med siderne som vist.
4. Nedenfor er en tegning af det femte trekantstal lavet i Geogebra.
   
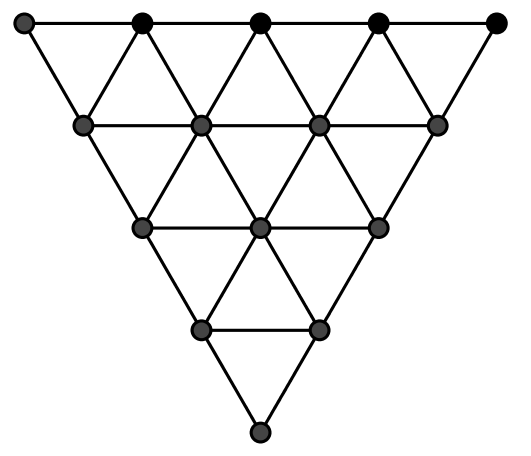
5. Nedenfor er skemaet udfyldtr. Det gøres ved at lægge tallet til venstre for et tomt felt sammen med tallet ovenfor som vist.
   
6. Formel 1 giver tallene: 1, 3, 7, 13...
   Formel 2 giver tallene: 1, 3, 6, 10...
   Det vil sige, at formel 2 er den rigtige.
7. Trekanttallet for n = 100 er (100² + 100)/2 = 10.100/2 = 5.050

Svar på opgave 5: Trekantbilleder

1. Trekanterne er vist nedenunder. Det ses på øjemål, at:
   
   Trekant 1 er retvinklet
   Trekant 2 er stumpvinklet
   Trekant 3 er stumpvinklet og ligebenet
   Trekant 4 er spidsvinklet og ligebenet
2. Hvis man måler efter ses det, at trekant 1 og 2 deler den øverste kant af rektanglet i to lige store dele. Desuden mødes toppunkterne af trekant 3 og trekant 4 i et punkt, der er skæringspunktet mellem midtnormalerne for rektanglets bredde og længde.
   
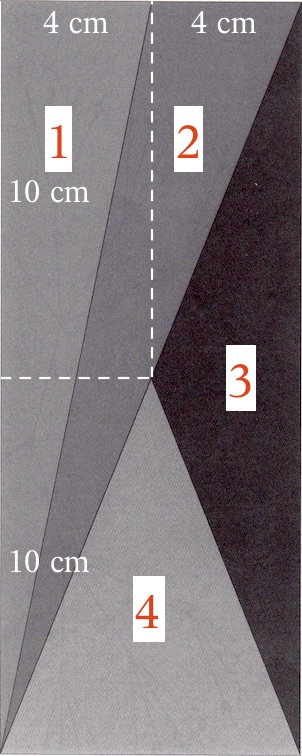
   Det vil sige, at den længste katete i trekant 1 er 20 cm og den korteste katete er 4 cm.
   Dermed er arealet af trekant 1 lig med 0,5·4·20 cm² = 40 cm²
3. Arealerne af trekant 1 og 2 er tilsammen halvdelen af rektanglets areal, da de udfylder den del af rektanglet, der ligger over den ene diagonal. De har samme areal, fordi de har samme grundlinje (4 cm) og samme højde (20 cm). Dermed er de hver en fjerdedel af rektanglets areal.
   Trekant 3 og 4 udfylder den anden halvdel af rektanglet og summen af deres arealer er dermed også halvdelen af rektanglets areal. De har samme areal fordi, de kan inddeles i fire ens trekanter (kaldet a) som vist på nedenstående figur.
   
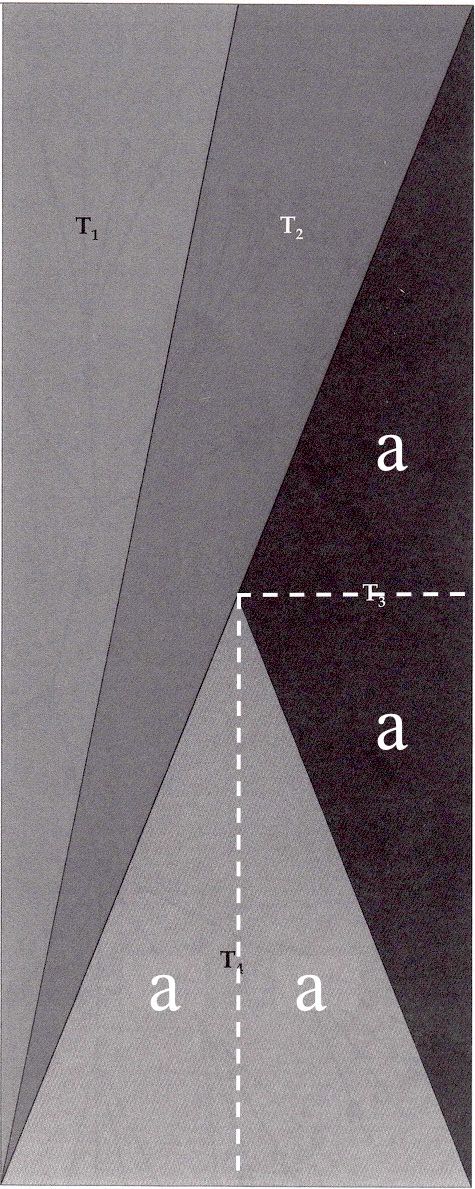
   Dermed har trekant 3 og 4 samme areal og deres areal er dermed også en fjerdedel af rektanglets areal. Dermed har alle trekanter samme areal.
4. Nedenfor er figuren spejlvendt omkring venstre side af rektanglet i Geogebra.
   

Svar på opgave 6: Kast med tetraeder

1. Sandsynligheden for at slå 4 er 1/4, da alle fire udfald er lige sandsynlige, og da summen af deres sandsynligheder skal give 1.
2. Den mindste sum er 1 + 1 + 1 = 3 og den største sum er 4 + 4 + 4 = 12
3. Antal muligheder med rød er 4. For hver af disse 4 muligheder er der 4 muligheder for sort, det vil sige, at der er i alt 4·4 = 16 muligheder for rød og sort.
   For hver af disse 16 muligheder er der endelig 4 muligheder for blå, dvs. i alt for de tre terninger er der 4·4·4 = 64 muligheder
4. Nedenfor er vist tælletræet fra svararket. For hver punkt yderst på træet er skrevet summen af tallene fra midten og ud.
   
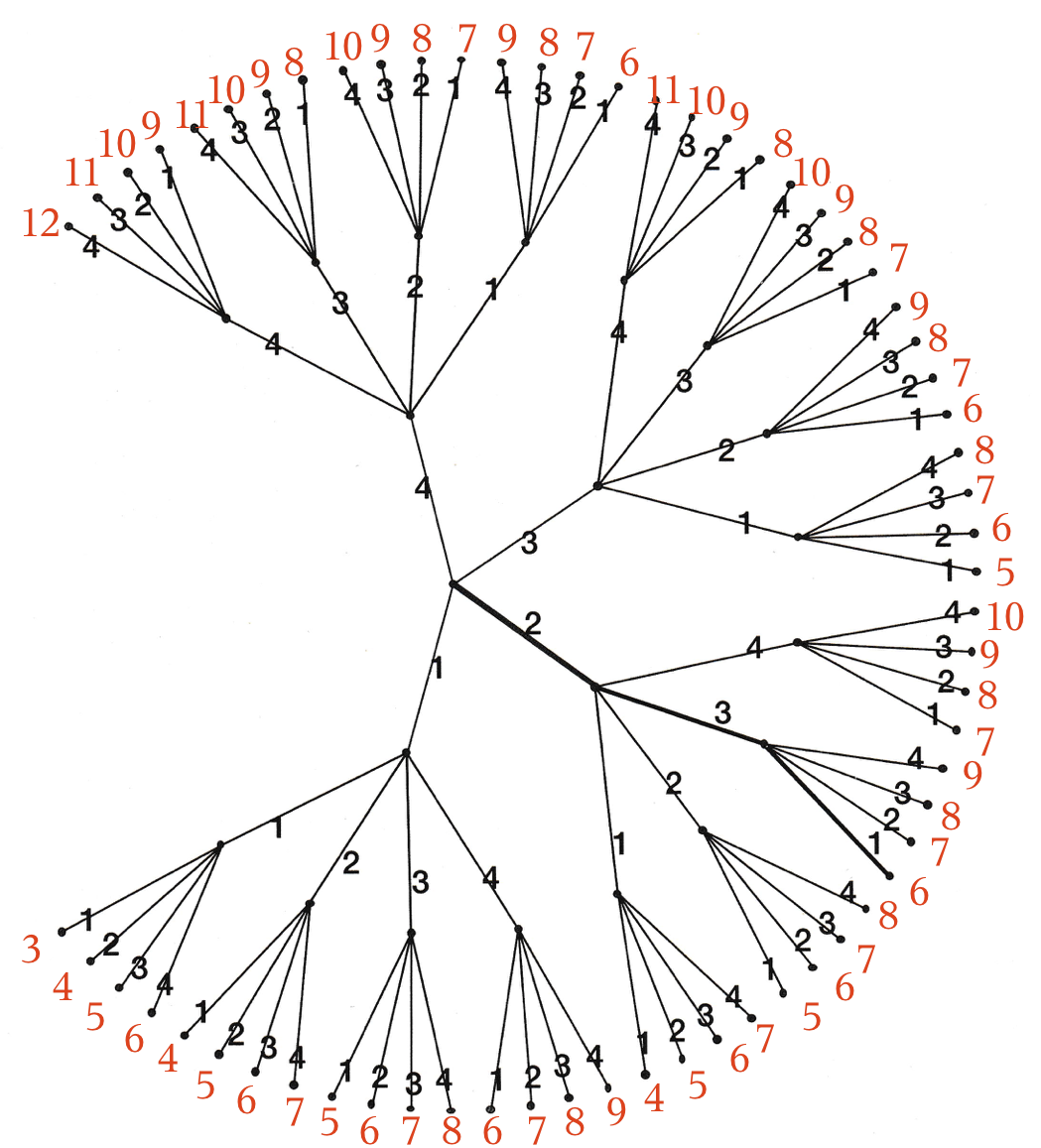
   Det ses, at 7 og 8 er de mest almindelige summer. De optræder 12 gange hver.
5. Summen 7 forekommer 12 gange ud af 64 mulige udfald. Dermed er sandsynligheden for summen 7 lig med 12/64 = 0,1875 = 18,8 %