Klik på en opgave for at se, hvordan den løses.
Givet følgende kemiske reaktion (ikke afstemt):
Sb + O2 + H+ → SbO+ + H2O
-
Gør rede for at der er tale om en redox-reaktion.
Svar på opgave 1:
-
Der er tale om en redox-reaktion eftersom Sb oxideres fra oxidationstrin 0 til oxidationstrin +3 (i SbO+). Samtidig reduceres O fra oxidationstrin 0 (i O2) til oxidationstrin -2 (i SbO+).
Nedenunder er vist stregformlen for en kemisk forbindelse.
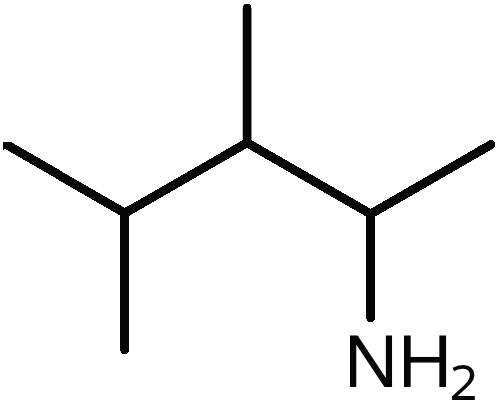
-
Tegn alle C'er og H'er (inklusive bindinger) på molekylet.
-
Gøre rede for at stoffet har to asymmetriske kulstofatomer.
-
Hvad er det systematiske navn for forbindelsen? (Der ses bort fra atomers orientering i rummet).
-
Hvad er det systematiske navn for forbindelsen, når -CH3 som vist nedenunder laves om til -COOH?
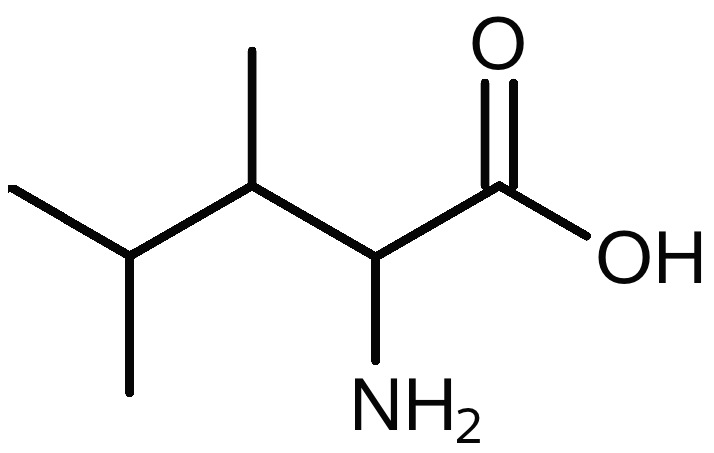
Svar på opgave 2:
-
Nedenfor er alle C'er og H'er tegnet ind med rødt. Hvert C skal have fire bindinger, hvert N tre, hvert O to og hvert H een binding.
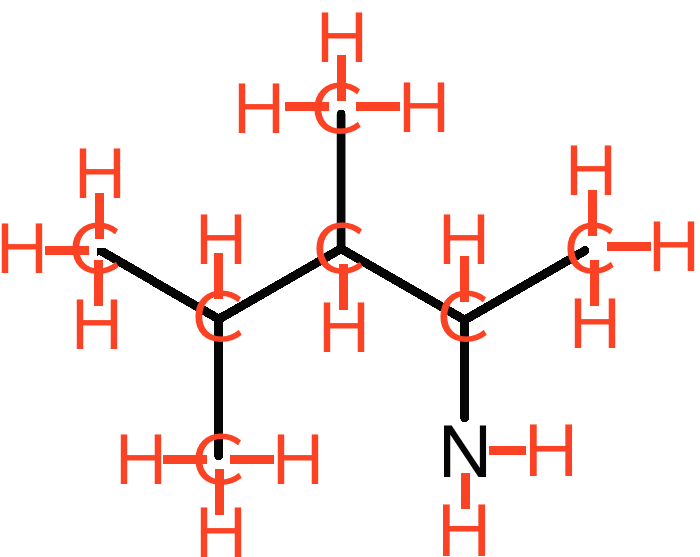
-
De to C-atom, som er vist med en rød stjerne nedenunder, er asymmetriske. Som det ses, så er de hver bundet til fire forskellige grupper.
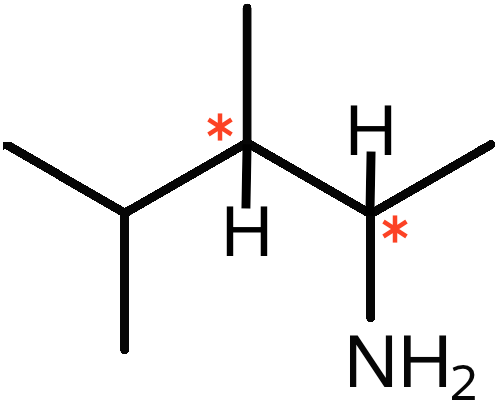
-
Man finder den længste kulstofkæde, der indeholder den vigtigste funktionelle gruppe (hovedgruppen). Længste kulstofkæde og hovedgruppen kaldes tilsammen stamforbindelsen. Her er vigstigste funktionelle gruppe NH2 (som hovedgruppe: -amin) og den længste kulstofkæde, der indeholder den, er pentan. Denne pentan nummereres, så NH2 får det lavest mulige placering (her 2). Dette er vist på tegningen nedenunder:
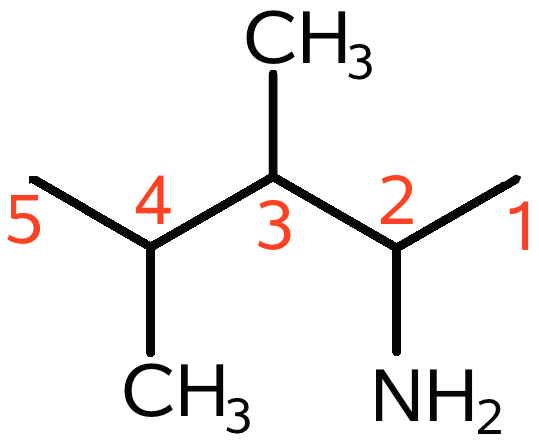
Man opskriver delene i stamforbindelsen, navnet på kulstofkæden bliver afterfulgt af den vigtigste funktionelle gruppes placering og navn. Tal og bogstav adskilles af bindestreg: pentan-2-amin.
På tegningen ovenfor er de to methyl-grupper på plads 3 og 4 fremhævet. Disse udgør sidegrupperne eller substituenterne i forbindelsen.
Sidegruppernes placeriger skrives efterfulgt af deres navn og til sidst navnet på stamforbindelsen. Der sættes "di" foran methyl for angive, at der er to af dem. Man sætter komma mellem tal, bindestreg mellem tal og bogstav og samler bogstaver.
Dette giver det systematiske navn: 3,4-dimethylpentan-2-amin
-
Den vigtigste funktionelle gruppe er COOH (som hovedgruppe: -syre). Den længste kulstofkæde, der indeholder den, er stadig pentan.
Stamforbindelsen nummereres så carboxylsyregruppen får lavest mulige nummer. Dette er vist nedenunder:
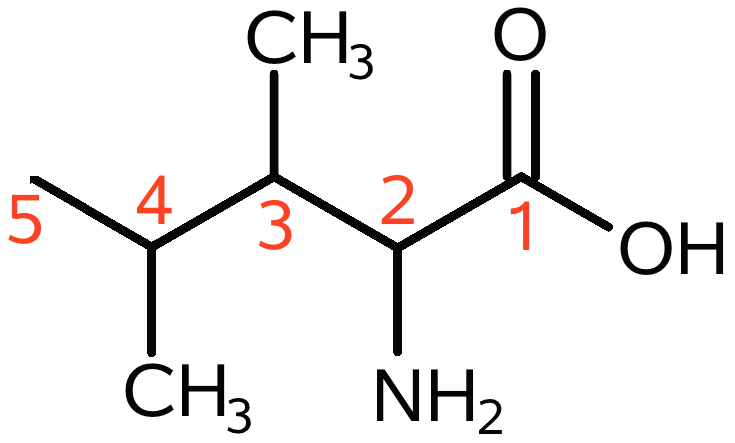
Stamforbindelsens navn er pentansyre. (En syre-gruppe sidder altid på plads nr. 1).
De to methyl-grupper på plads 3 og 4 er sidegrupper som før. Derudover er der en amino-sidegruppe på plads nummer 2.
Man opstiller sidegrupperne i alfabetisk orden med deres placering og antal foran ders navn. Til sidst opskrives stamforbindelsen.
Dette giver det systematiske navn: 2-amino-3,4-dimethylpentansyre
Nedenunder er vist nogle organisk kemiske forbindelser.
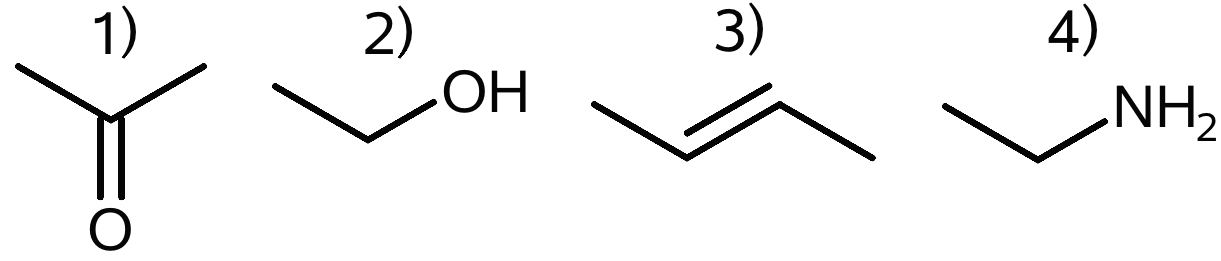
-
Navngiv de funktionelle grupper i 1-4)
-
Hvilken funktionel gruppe kan deltage i en syre/base reaktion?
-
Hvilken funktionel gruppe kan affarve brom-vand?
-
Hvilken funktionel gruppe kan oxideres til en carboxylsyre?
-
Hvilken funktionel gruppe kan reagere med 2,4-dinitrophenylhydrazin?
Svar på opgave 3:
-
1) Carbonyl-gruppe (aldehyd eller keton kan også godkendes).
2) Hydroxyl-gruppe (alkohol eller primær alkohol kan også godkendes).
3) Alken.
4) Amino-gruppe (eller amin evt. primær amin).
-
Aminogruppen (4) kan optage H+ og virke som base.
-
Alkenen (3) kan affarve brom-vand ved en additionsreaktion.
-
Hydroxyl-gruppen (2) kan, når den som her er endestillet, oxideres til en carboxylsyre.
-
Carbonyl-gruppen (1) kan reagere med 2,4-dinitrophenylhydrazin og danne gult bundfald.
Nedenunder er vist en organisk kemisk reaktion.

-
Hvilken type reaktion er der tale om?
-
Hvilken betydning han det have at tilsætte koncentreret H2SO4 til reaktionsblandingen?
-
Hvilken type er den modsatte reaktion?
Svar på opgave 4:
-
Det er en esterdannelse, (evt. estersyntese) eller en kondensation (en reaktion, hvor der dannes vand).
-
H2SO4 virker som katalysator og binder det vand som dannes, hvorved ligevægten forskydes mod højre.
-
Den modsatte reaktion hedder hydrolyse af ester (sønderdeling af ester ved hjælp af vand).
Eddikesyre er en svag syre, hvor pKs = 4,76. Beregn pH i følgende opløsninger:
-
0,15 M eddikesyre.
-
35 ml 0,2 M eddikesyre, der er blandet med 45 ml 0,1 M NaOH.
Svar på opgave 5:
-
Man bruger formlen for pH i opløsning af svag syre. Cs står for den formelle koncentration af eddikesyre:
pH = 0,5·(pKS - log(CS)) ⇒
pH = 0,5·(4,76 - log(0,15) ⇒
pH = 0,5·(4,76 - log(0,15)) ⇒
pH = 2,8
-
Man bruger formlen for pH i en buffer (Henderson-Hasselbalch-ligningen). I det følgende er...
nS stofmængden af eddikesyre efter blanding,
nB stofmængden af eddikesyres korresponderende base efter blanding,
nS,0 stofmængden af eddikesyre før blanding,
nNaOH stofmængden af NaOH før blanding,
CS den formelle koncentration af eddikesyre før blanding,
VS rumfanget af eddikesyre før blanding og
CNaOH den formelle koncentration af NaOH før blanding.
pH = pKS + log(nB/nS) ⇒
pH = pKS + log(nNaOH/(nS,0 - nNaOH)) ⇒
pH = pKS + log(CNaOH·VNaOH/(CS·VS - CNaOH·VNaOH)) ⇒
pH = 4,76 + log(0,1·0,045/(0,2·0,035 - 0,1·0,045)) ⇒
pH = 4,76 + log(1,8) ⇒
pH = 5,0
Figuren nedenunder viser titrerkurven for en svag syre, der er titreret med NaOH. Omslagspunktet er ved 10,0 ml tilsat NaOH.
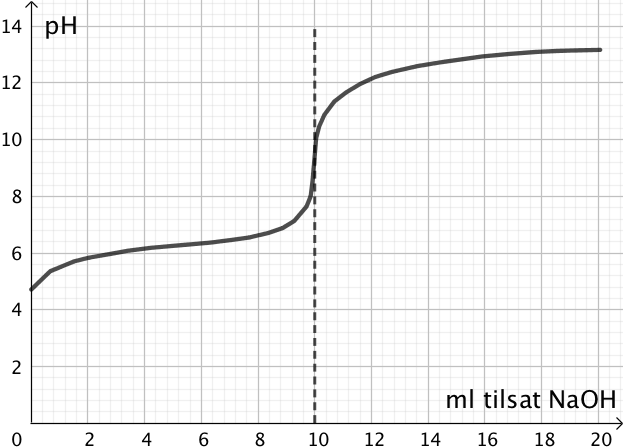
-
Hvad er pH i opløsningen ved omslag?
-
Find pKs for syren.
Svar på opgave 6:
-
pH i omslagspunktet aflæses af kurven, som det pH der gælder ved 10,0 ml tilsat NaOH.
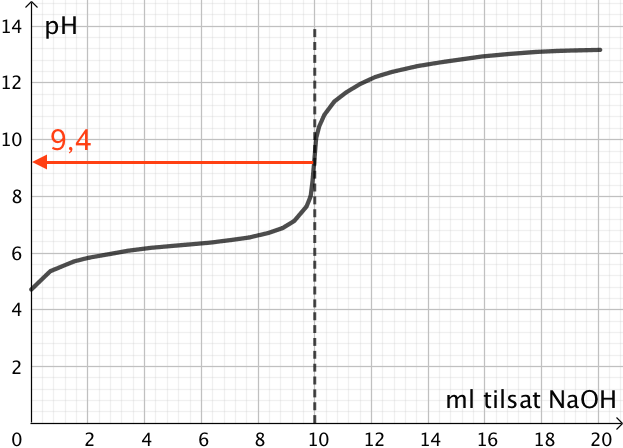
pH aflæses til 9,4
-
pKS for syren aflæses som pH ud fra kurven som pH midt mellem start og omslag dvs. som pH for 5,0 ml tilsat NaOH
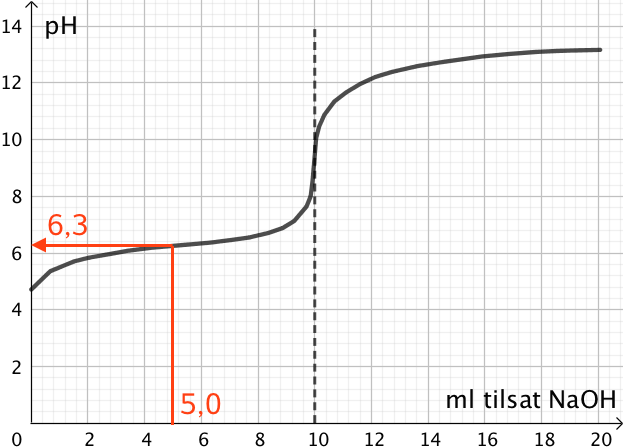
Dvs pKS for syren er 6,3
Figuren nedenunder viser Bjerrumdiagrammet for en diprot syre H2A.
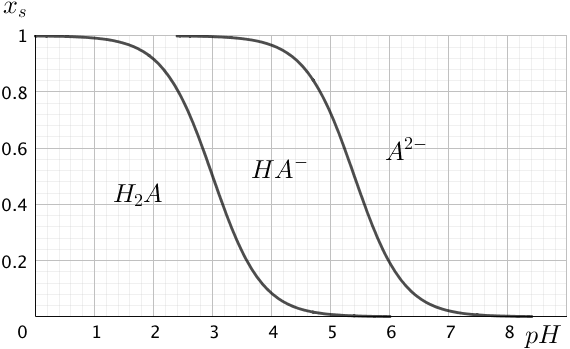
-
Bestem pKs for H2A.
-
Hvad er molbrøken for A2- ved pH = 6,0?
Svar på opgave 7:
-
Den kurve, som er længst til venstre i Bjerrumdiagrammet, gælder for ligevægten H2A ⇌ HA- + H+.
Dermed kan pKS til H2A kan aflæses af kurven som den pH værdi, hvor xs for H2A er 0,5, eller hvor [H2A] = [HA-].
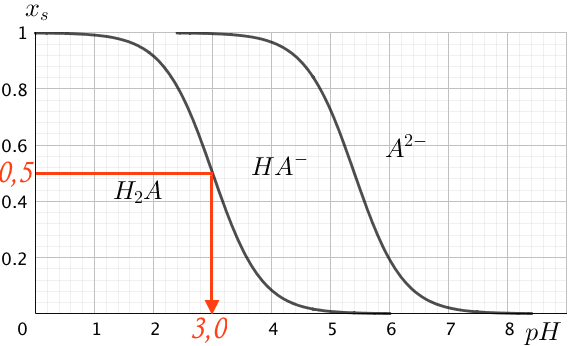
Det ses, at pKS for H2A er 3,0
-
Ved pH = 6,0 er kurven for H2A/HA- ligevægten i bunden af diagrammet, og man kan se bort fra [H2A].
Dermed kan man finde molbrøken af A2- som basebrøken (x) af A2- ved pH = 6,0. Dette er vist med rødt på diagrammet nedenfor:
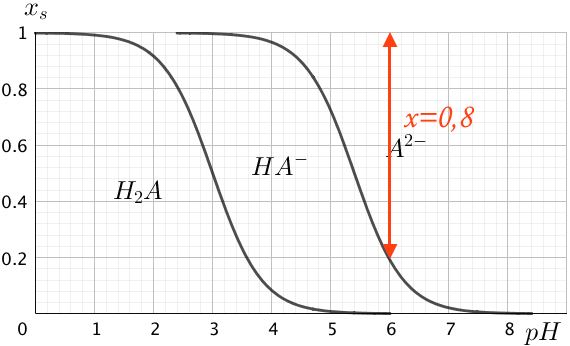
Det ses at molbrøken af A2- kan aflæses til 0,8 ved pH = 6,0.
En monoprot syre med molmassen 123,1 g/mol opløses i vand så opløsningens rumfang er 250,0 ml.
Af denne opløsning overføres de 10,0 ml med pipette til en kolbe, som fyldes op med vand til rumfanget 50,0 ml.
Hele den færdige opløsning titreres til omslag med 11,3 mL 0,105 M NaOH.
-
Hvad er massen af syren fra start?
Svar på opgave 8:
-
Man sætter massen af stof = m, molmassen = M og stofmængden = n. Der gælder at m = n·M.
Efter fortyndingen overføres (1/25)·n til kolben, hvor titreringen foregår.
Da syren er monoprot, så gælder at (1/25)·n = nNaOH = CNaOH·VNaOH, hvor
nNaOH er stofmængden af tilsat NaOH,
CNaOH er koncentrationen af NaOH i den tilsatte basiske opløsning (titrator) og
VNaOH er volumenet af tilsat NaOH.
Dvs. (1/25)·n = (0,105 M)·(0,0113 L) ⇒ n = 25·(0,105 M)·(0,0113 L) = 0,0297 mol
Den oprindelige masse af syre er derfor: (0,0297 mol)·(123,1 g/mol) = 3,66 g
Et organisk molekyle har molmassen M = 74,0 g/mol. Det har følgende grundstof-sammensætning i masseprocent:
C: 48,6 %
H: 8,1 %
O: 43,2 %
-
Hvad er stofets bruttoformel?
Svar på opgave 9:
-
Molekyleformlen kan skrives: CxHyOz. Her er x antal C i molekylet, y antal H i molekylet og z antal O i molekylet.
Et molekyle har massen M. Massen af C i et molekyle er x·MC. Masseprocenten af C i et molekyle er x·MC/M. Tilsvarende for de andre grundstoffer. Det giver:
x·MC/M = 48,6 % ⇒ x·(12,01 g/mol)/(123,1 g/mol) = 0,486 ⇒ x = 3
y·MH/M = 8,1 % ⇒ x·(1,008 g/mol)/(123,1 g/mol) = 0,081 ⇒ y = 6
z·MO/M = 43,2 % ⇒ x·(16,00 g/mol)/(123,1 g/mol) = 0,432 ⇒ z = 2.
Dvs. molekyleformlen er C3H6O2
Et organisk stof består af en kulbrintekæde med 5 C-atomer. På det ene sidder en amino-gruppe.
-
Argumenter for at stoffets vandopløselighed vokser med faldende pH.
Svar på opgave 10:
-
Stoffet indeholder en amino-gruppe, der ved lave pH-værdier kan optage et H+ og dermed blive en ion. Ioner har høj vandopløselighed og dermed stiger stoffets vandopløselighed ved faldende pH.
Stoffet A omdannes ved en reaktion. Nedenunder er vist en tabel over målepunkter for koncentrationen af A som funktion af tiden i denne omdannelse.
| [A]/mM | 8,37 | 3,34 | 1,33 | 0,53 | 0,21 |
| Tid/timer | 0,50 | 1,00 | 1,50 | 2,00 | 2,50 |
-
Vis at reaktionen er af første orden.
-
Hvad er halveringskonstanten for reakionen?
Svar på opgave 11:
-
Man afbilder ln([A]) som funktion af tiden. Hvis man får en ret linje, så er reaktionen af første orden.
Nedenunder er afbildningen vist:
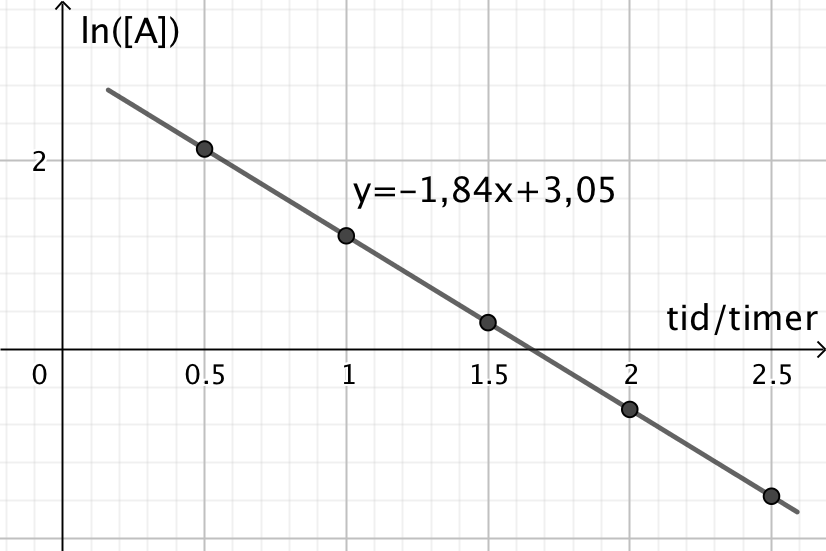
Da punkterne ligger på en ret linje, så er reaktionen af første orden.
(Man kan for en sikkerheds skyld afbilde [A] som funktion af tiden for at teste om reaktionen er af nulte orden eller afbilde [A] som funktion af 1/tiden for at teste om, den er af anden orden. Ingen af disse to afbildninger må give en ret linje.)
-
Halveringskonstanten er ln(0,5)/k, hvor k er hældningen til kurven ovenfor.
Det ses, at k =-1,84 timer-1, hvorved halveringskonstanten bliver: (-0,69/(-1,84)) timer = 0,38 timer
Stoffet B er vandopløseligt og absorberer lys ved en bestemt bølgelængde. Nedenfor er vist en kurve for absorbansen af stoffet i koncentrations-intervallet 1,0 μM - 9,0 μM. Ligningen for kurven er vist.
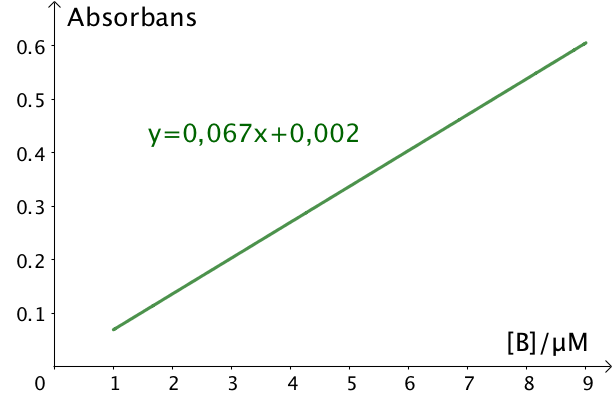
Fra en opløsning af B udtages en prøve som fortyndes 50 gange. Prøven har absorbansen 0,30.
-
Hvad er koncentrationen af stoffet B i den ufortyndede opløsning?
Svar på opgave 12:
-
Man har fået oplyst ligningen: y = 0,067·x + 0,002, hvor y er absorbansen og x er den tilhørende koncentration af stoffet.
Her er y = 0,30, og man finder det tilhørende x: 0,30 = 0,067·x + 0,002 ⇒ x = [(0,30 - 0,002)/0,067] μM = 4,45 μM. Dette skal koncentreres 50 gange og man får, at koncentrationen i den oprindelige prøve er 50·4,45 μM = 223 μM
Nedenfor er vist et H-NMR spektrum for esteren methylpropanoat CH3CH2COOCH3. Under spektrummet er vist det kemiske skift. Integralet under toppene er ikke angivet.
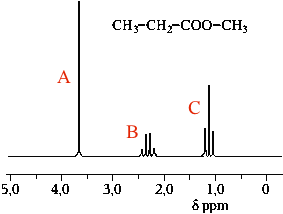
-
Giv en forklaring til toppene A-C.
-
Angiv mulige integraler for de tre toppe.
Svar på opgave 13:
-
Nedenfor er vist hvilken gruppe af H'er, der hører til hvilken top.
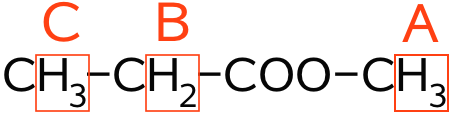
Toppen A kommer af de 3 H'er, der sidder på methyl i alkohol-delen til højre i esteren. Den har et højt kemisk skift på 3,7, fordi de tre H'er sidder på et C, der er bundet direkte til et O. Af samme grund er toppen en singlet, idet der ikke er nogen H'er på O'et, der kan koble med de tre H'er.
Toppen B kommer fra de to H'er, der sidder på det midterste C i stoffet. Toppen er en kvartet, da H'erne på C-atomet kobler med de tre H'er der sidder på C'et yderst til venstre i den viste stofformel. Koblingsmønsteret følger n + 1 reglen, hvor n er antallet af H'er på nabo C-atomet. Det middelhøje kemiske skift på 2,3 skyldes, at de to H'er deshieldes af O'et på det andet nabo C-atom.
Toppen C kommer fra de tre H'er, der sidder på det C, der er længst til venstre i stofformlen. Toppen er en triplet, da H'erne på C-atomet kobler med de to H'er der sidder på C'et i midten. Koblingen følger n + 1 reglen. Det lave kemiske skift på 1,2 skyldes, at de tre H'er ikke deshieldes af O på et nabo C-atom, men kun af O'er der sidder længere væk.
-
Integralet af en top i et H-NMR spektrum er et multiplum af antallet af H'er, der skaber toppen. Dermed er integralerne for A, B og C: 3, 2 og 3, eller disse tal gange med samme naturlige tal.
En bestemt kemisk reaktion foregår ved 25 °C og 1,00 bar.
Der gælder, at ΔHΘ25°C = -172 kJ/mol og ΔSΘ25°C = -330 J/(mol·K).
-
Vis at reaktionen forløber spontant fra venstre mod højre ved denne temperatur og dette tryk.
-
Hvad er ligevægtskonstanten, Keq, for reaktionen (Keq antages at være dimensionsløs).
-
Hvad er ligevægtskonstanten for reaktionen ved 100 °C og 1,00 bar.
Antag at ΔHΘ og ΔSΘ er uafhængige af temperaturen.
Svar på opgave 14:
-
Reaktionen forløber spontant ved 25 °C og 1,00 bar, da den frie Gibbs energi er negativ (ΔGΘ25°C < 0).
Man får nemlig, idet T er den absolutte temperatur for reaktionen:
ΔGΘ25°C = ΔHΘ25°C - T·ΔSΘ25°C ⇒
ΔGΘ25°C = -172·103 J/mol - (273 + 25 K)·(-330 J/(mol·K)) ⇒
ΔGΘ25°C = −73.660 J/mol
-
Ligevægstkonstanten findes ved hjælp af formlen (hvor R er gaskonstanten):
Keq = exp(-ΔGΘ25°C/(R·T)), der giver:
Keq = exp(-(−73660 J/mol)/((8,413 J/(mol·K))·(298 K))) = 5,75·1012
-
Man finder ΔGΘ100°C dvs. den frie Gibbs energi ved 100 °C for reaktionen. Under forudsætningen om, at ΔHΘ og ΔSΘ er uafhængige af temperaturen, så får man:
ΔGΘ100°C = ΔHΘ25°C - [(100 + 273) K]·ΔSΘ25°C
ΔGΘ100°C = -172000 J/mol - (373 K)·(-330 J/(mol·K)) = -48.910 J/mol
Keq,100°C = exp(-ΔGΘ100°C/(R·T)) ⇒
Keq,100°C = exp(-(-48.910 J/mol)/((8,314 J/(mol·K))·(273+100 K))) ⇒
Keq,100°C = 7,07·106
(Brug af van't Hoff's ligning er i princippet det samme.)
Man har følgende reaktion, hvor alle stoffer er på gas-form:
A ⇌ B + C
Reaktionen foregår ved 300 °C i en beholder med et konstant rumfang på 2,50 L. Blandingen antages at opføre sig som en ideal gas.
-
Hvad er dimensionen af ligevægtskonstanten til reaktionen?
-
Hvad sker med totaltrykket, når reaktionen forløber mod højre ved fastholdt volumen?
-
Hvad er partialtrykket af B ved ligevægt?
-
Hvad er stofmængden af A ved ligevægt?
Fra starten er partialtrykket af A lig med 0,24 bar. Ligevægtskonstanten for reaktionen er K = 0,15 bar.
Svar på opgave 15:
-
Ligevægtskonstanten er pB·pC/pA, hvor p står for partialtryk. Da pA, pB og pC alle har enheden bar, så har ligevægtskonstanten dimensionen bar·bar/bar = bar
-
Totaltrykket stiger, idet antallet af molekyler i gassen stiger. Når stofmængden af gas stiger, så vil det samlede tryk også stige.
-
Da V, R og T er konstante, så er partialtrykket proportional med og stofmængden for hver enkelt gas.
Man kan opstille følgende partialtryk for A, B og C:
A ⇌ B + C
Start: pA,0 0 0
Ligevægt: pA = pA,0 - pB pB pC = pB
Her er pA,0 start-partialtrykket af A, mens pA, pB, pC er ligevægts-partialtrykket af henholdsvis A, B og C.
pA = pA,0 - pB følger af, at pA = nA·R·T/V, hvor nA er stofmængden af A. Desuden gælder: nA = nA,0 - nB, der giver pA = nA·R·T/V = (nA,0 - nB)·R·T/V = nA,0·R·T/V - nB·R·T/V = pA,0 - pB.
Ligningen nA = nA,0 - nB følger af, at A og B har samme koefficient i reaktionsskemaet. Tilsvarende gælder pB = pC også, fordi B og C har samme koefficient.
Dermed gælder: Keq = (pB)2/(pA,0 - pB). Man indsætter Keq = 0,15 bar og pA,0 = 0,24 bar:
0,15 bar = (pB)2/(0,24 bar - pB) ⇒ pB = 0,129 bar
Dvs. partialtrykket for B ved ligevægt er 0,13 bar
-
Idealgasligningen giver:
pA·V = nA·R·T ⇒ nA = pA·V/(R·T) ⇒ nA = (pA,0 - pB)·V/(R·T), hvor
nA og pA er henholdsvis er stofmængde og partialtryk af A ved ligevægt.
I udtrykket nA = (pA,0 - pB)·V/(R·T) indsættes:
pA,0 = 0,24 bar,
pB = 0,13 bar,
V = 2,5 L,
R = 0,08314 bar·L/(mol·K) og
T = (273 + 300) K = 573 K.
Man får: nA = (0,24 bar - 0,13 bar)·(2,5 L)/((0,08314 bar·L/(mol·K))·(573 K)) = 0.0058 mol.
Dvs. stofmængden af A ved ligevægt er 5,8·10-3 mol