Svar på opgave 1: Timianolie

1. På billedet nedenunder er de manglede C'er og H'er indtegnet.

   

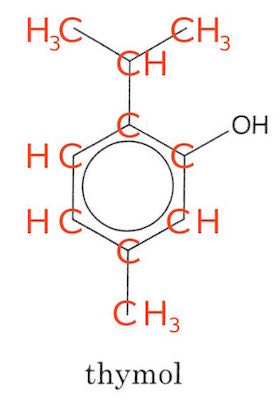
2. På billedet nedenunder er de funktionelle grupper vist og navngivet.

   

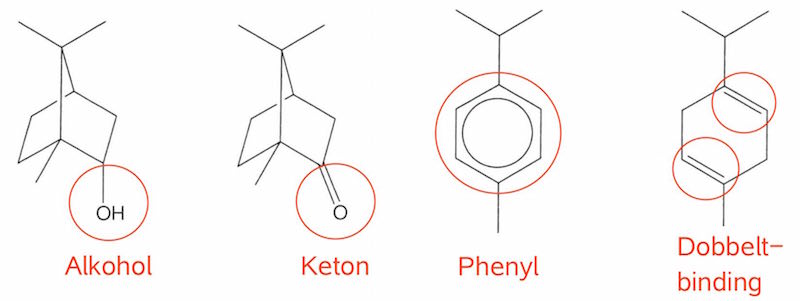
3. Stoffer som indeholder dobbeltbindinger affarver bromvand ved addering af Br. Dvs. γ-terpen affarver bromvand og er dermed stof 2.

   2,4-dinitrophenylhydrazin danner gult bundfald med C=O grupper, dvs. med aldehyder og ketoner. Dermed er stof 4 campher.

   Hydroxygrupper giver et bredt absorptionsbånd ved ca. 3400 cm^-1 på IR spectret. En benzenring giver bånd ved 1600 cm^-1 og 1470 cm^-1. Dette kan bruges til at identificere borneol og p-cymen.

   Thymol vil vise begge typer af bånd.

Svar på opgave 2: Medicin til behandling af epilepsi

1. På nedenstående billede er et asymmetrisk kulstofatom markeret med *. Et H-atom indtegnet for at vise, at det påhældende C-atom er bundet til fire forskellige grupper. Det asymmetriske kulstofatom gør, at stoffet udviser spejlbilledisomeri.

   

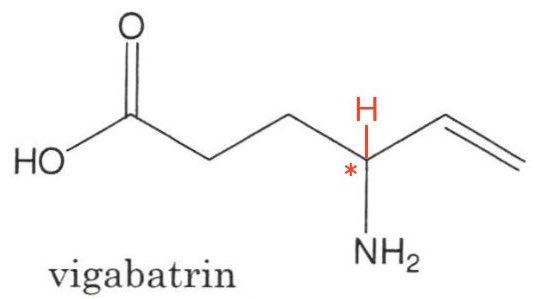
2. Man finder den højst prioriterede funktionelle gruppe, som er carboxylsyren. Dernæst finder man den længste kulstofkæde, som indeholder syregruppen. Kulstofkæden nummereres, så C-atomet i syregruppen får nummer 1. Dette er samlet vist nedenunder:

   

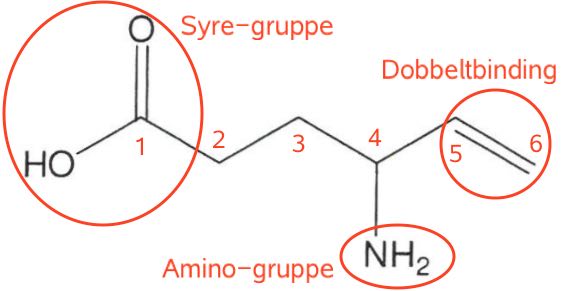
   Den længste kulstofkæde er hexen. Dobbeltbindingen sidder, som det ses ovenfor, mellem C-5 og C-6. Sidegruppen -NH₂ (en amino-gruppe) sidder på C-4.

   Man har:

   - Vigtigste funktionelle gruppe: syre

   - Længste kulstofkæde, der indeholder syren: hex-5-en

   - Sidegruppe på denne kæde: 4-amino.

   Dette sættes sammen til: 4-aminohex-5-ensyre

3. Der gælder følgende formel for molmassen af H₂A (M_H2A):

   M_H2A = m_H2A/n_H2A, hvor

      m_H2A = 0,317 g er massen af H₂A i prøven og

      n_H2A er antal mol H₂A.

   Molmassen af H₂A beregnes ud fra titrerkurven. Man aflæser, at der er tilsat 35 mL NaOH-opløsning ved det store omslag. Her er alle H⁺ neutraliseret, og der gælder:

   2·n_H2A = n_NaOH ⇒ n_H2A = 0,5·n_NaOH, her er

      n_H2A antal mol H₂A i prøven og

      n_NaOH er det antal mol NaOH, som er tilsat ved titrering.

   Der gælder desuden, at C_NaOH = n_NaOH/V_NaOH ⇒ n_NaOH = C_NaOH·V_NaOH, hvor

      C_NaOH = 0,124 M er koncentrationen af NaOH (titrator)

      V_NaOH = 35 mL er det tilsatte volumen af NaOH-opløsning, som aflæses af kurven som vist:

   

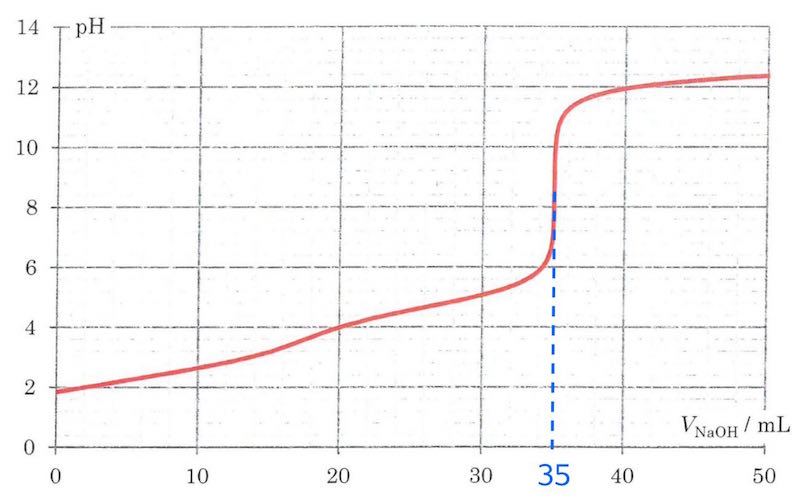
   Man har nu samlet for molmassen af H₂A:

   M_H2A = m_H2A/(C_NaOH·V_NaOH) =

   (0,317 g)/[(0,124 M)·(35 mL)] = (0,317 g)/[(0,124 mol/L)·(35·10^-3 L)] =

   0,317/(0,124·35·10^-3) g/mol = 146 g/mol

4. Man bestemmer molekyle formlen for stoffet, som har den foreløbige formel: C_xH_yO_z. Der gælder:

   x = (41,11 %)·(146/12) = 5,00 ≈ 5

   y = (4,14 %)·(146/1) = 6,04 ≈ 6

   z = (54,75 %)·(146/16) = 5,00 ≈ 5

   Dvs. molekyleformlen for H₂A er C₅H₆O₅.

   Man ved, at syren er organisk og dihydron, og derfor, at der indgår 2 carboxylsyre­grupper i den. Man har den delvise strukturformel: C₃H₄O(COOH)₂. Man betragter dernæst ¹H-NMR-spektret for at se, hvilke andre grupper, som må indgå:

   

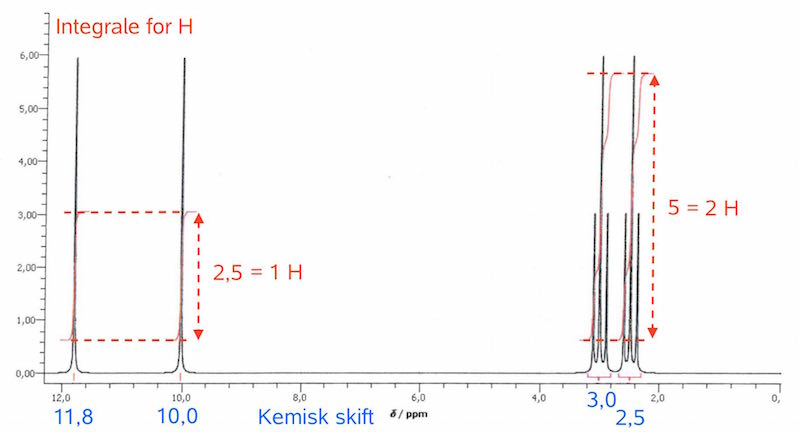
   De to toppe til venstre stammer fra de to -COOH grupper. Det følger af, at toppene er singletter, har integralet 1 hver og har et kemisk skift i intervallet 10-12. At de er singletter følger af, at H'et i COOH sidder på et O og ikke et C. At H'et i -COOH har kemisk skift i intervallet 10-12 skyldes, at det deshieldes af to O'er der sidder på samme C-atom, som det selv er forbundet til. At integralet over toppene svarer til 1 H følger af, at der er 6 H, og at det målte integrale over hver top svarer til en sjettedel af integralet over alle H'erne.

   Dermed er der to toppe tilbage. De ligger i intervallet 2,5-3 med hensyn til kemisk skift, har hver 2 H og er tripletter. Dermed må de stamme fra 2 CH₂- grupper, der er forbundet. At de har et lavt kemisk skift passer med, at C kun i ringe grad deshielder H. At de er tripletter viser, at de 2 CH₂- grupper sidder ved siden af hinanden i kulstofkæden. Splittet på 3 i hver top viser nemlig, at der er 2 H på det tilstødende C.

   Dette giver den delvise strukturformel (-CH₂-CH₂-)(>C=O)(-COOH)₂, der har følgende mulighed:

   

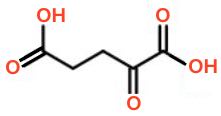
   Derfor må H₂A være α-Ketoglutarsyre, som er det viste stof.

   På billedet nedenunder er toppene i ¹H-NMR-spektret forklaret.

   

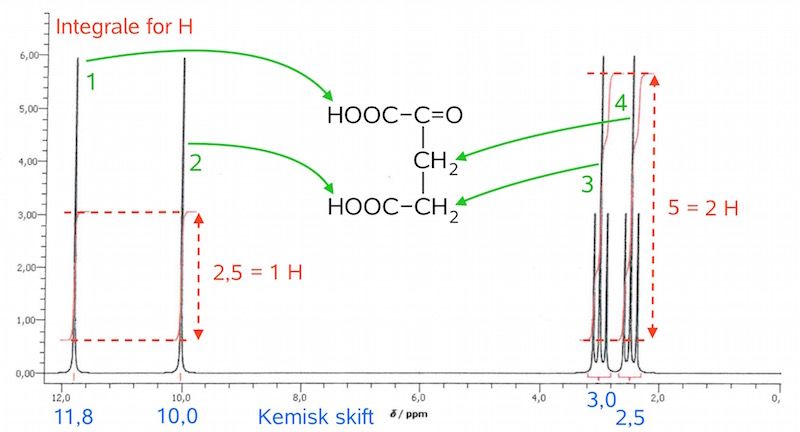
   1) Integrale = 1 H, skift = 11,8, split = singlet. Det høje kemiske skift skyldes, at det både deshieldes af O fra COO og C=O. Det er en singlet, fordi H er bundet til O og ikke C.

   2) Integrale = 1 H, skift = 10,0, split = singlet. H'et har et skift, der er mindre end det forrige, fordi H'et kun deshieldes O'erne fra dens egen carboxylgruppe og ikke af et O på det tilstødende C-atom. Det er en singlet af samme grund som før.

   3) Integrale = 2 H, skift = 3, split = triplet. H'erne har et lavt kemisk skift, fordi de kun deshieldes af det C, som det sidder på og derudover to O fra den stilstødende COOH gruppe. Det er en triplet, da der er 2 H-atomer på det tilstødende C-atom.

   4) Integrale = 2 H, skift = 2,5, split = triplet. H'erne har et endnu lavere skift end den foregående, fordi de kun deshieldes af et O på det tilstødende C-atom og ikke to som ovenfor. Det er en triplet af samme grund som den forrige top.

Svar på opgave 3: Forgrenede aminosyrer i muskler

1. Den formelle koncentration af leucin (C) beregnes med formlen

   C = m/M·V, hvor

      m = 1250 mg er massen af leucin,

      M = 131,17 g/mol er molmassen af leucin og

      V = 330 mL er opløsningens rumfang.

   Man får C = (1250·10^-3 g)/[(131,17 g/mol)·(330·10^-3 L)] = 1250/(131,17·330) mol/L = 28,9 mM

2. Aminosyrerne kan sættes sammen ved hjælp af peptidbindinger som vist nedenunder med røde pile:

   

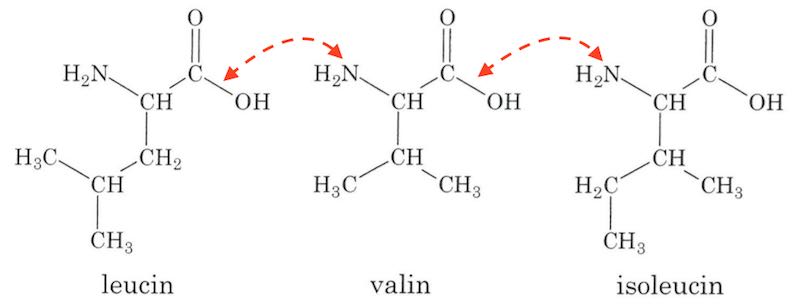
   I hver peptidbinding fraspaltes et H₂O-molekyle, dvs. der er tale om en kondensations-reaktion. Nedenfor er vist, hvordan aminosyrerne kan sættes sammen i en tripeptid.

   

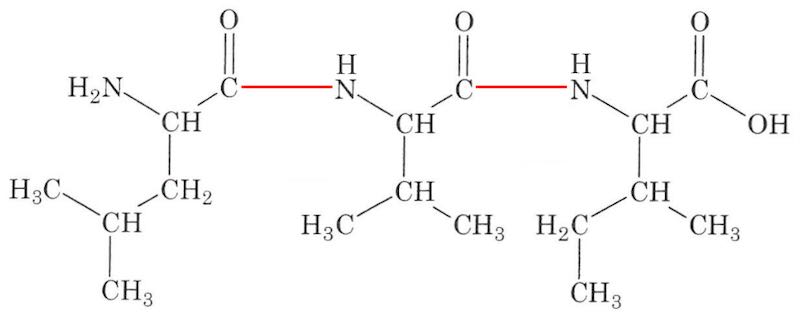
3. Nedenfor er vist grafen for v(c). Det ses, at når startkoncentrationnen af leucin øges, så går initialhastigheden mod 0,56 M/min. Dette er vist med en grøn vandret linje.

   

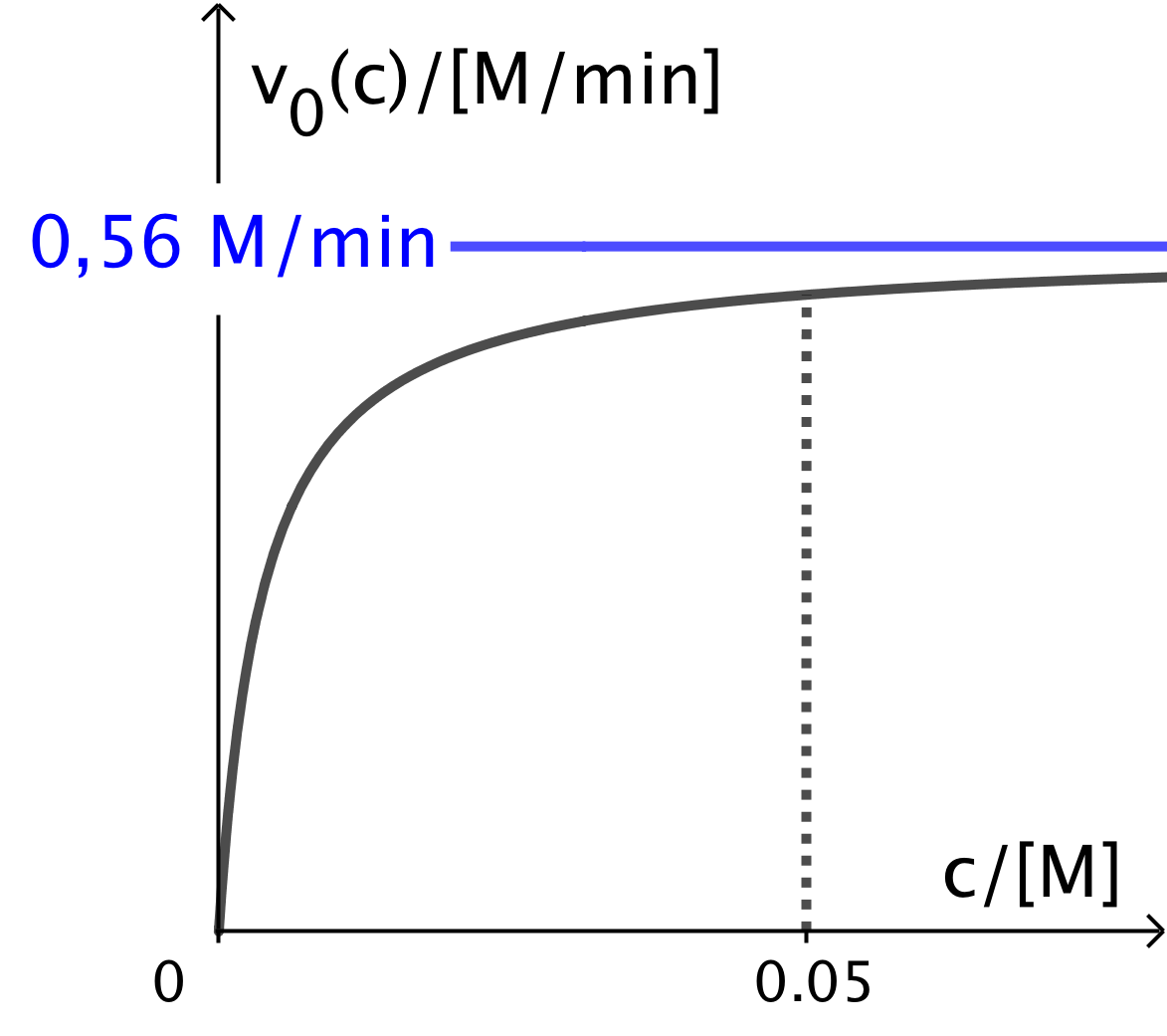
   Fra en bestemt initialkoncentration og derover vil hastigheden være så tæt på 0,56 M/min, at man ikke kan måle nogen ændring. Over den koncentration kan man regne reaktionen for at være af nulte orden, idet v(c) er konstant og ca. lig med 0,56 M/min.

   På grafen er valgt koncentrationen c(leucin) = 0,05 M, som den koncentration, jvor intervallet for nulte ordens reaktion starter. Dvs. intervallet, hvor reaktionen kan anses for at være nulte orden er c(leucin) ∈ ]0,05 M;∞[

   På grafen nedenunder er yderlige vist, at for koncentrationen gående mod 0, så vil grafen nærme sig en ret linje. Denne linje er v(c) = (a/b)·c = 147·c for leucin. Grafen nærmer sig denne linje for c ≈ 0,002 M.

   

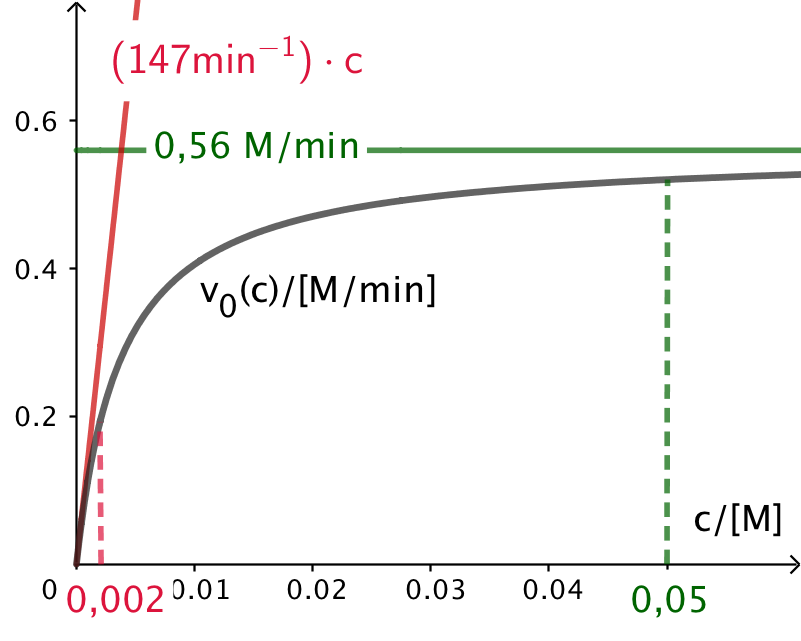
   I opgaven ses på udtrykket v(0) = a·c(0)/(b+c(0)), dvs. start-reaktionshastigheden som funktion af startkoncentrationen af leucin. Man kan imidlertid bruge samme udtryk til at vurdere v(t), dvs. reaktionshastigheden som funktion af tiden, idet man blot indsætter c(t), der er koncentrationen af leucin som funktion af tiden. Man får:

   v(t) = a·c(t)/(b+c(t))

   Hvis b<<c(t) får man v(t) ≈ a, der som nævnt giver en nulte ordens reaktion.

   Hvis b>>c(t) får man v(t) ≈ (a/b)·c(t), der giver en første ordens reaktion, idet a/b er en konstant.

   Hvis man lader reaktionen starte ved en høj koncentration som f.eks. 0,1 M, så vil man først se grafen for c(t) være en ret linje med negativ hældning et stykke tid indtil koncentrationen er faldet til under 0,05 M. Derefter vil der være en overgang, der ikke følger nogen bestemt orden. Til sidst - for c < 0,002 M - vil grafen være en aftagende eksponentialfunktion, der svarer til en reaktion af første orden. Dette er skitseret nedenunder:

   

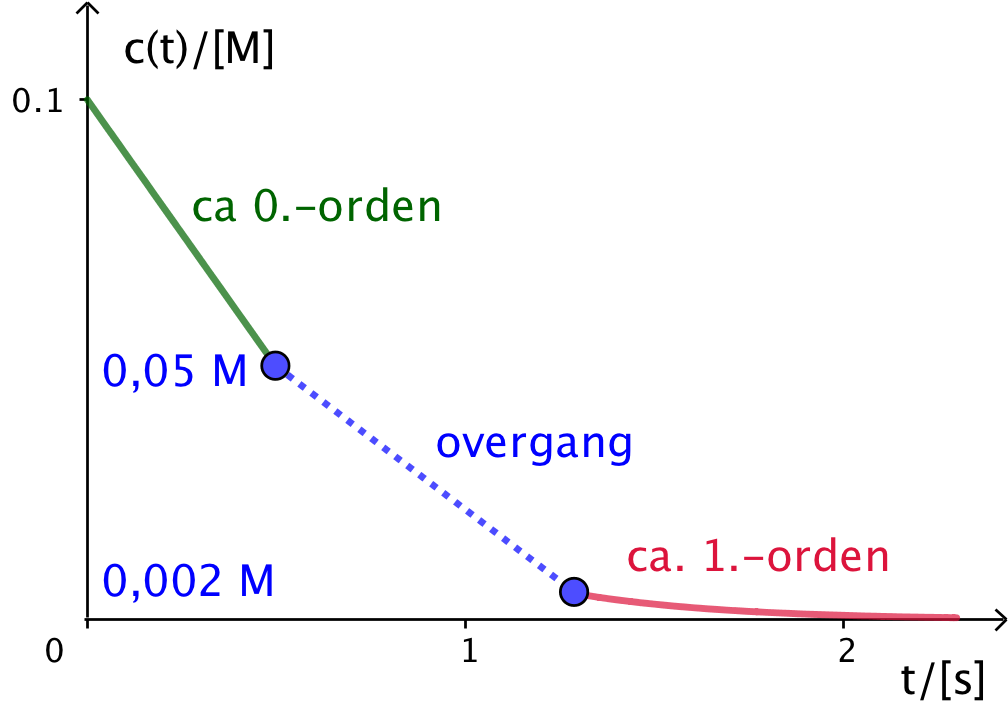
4. Volumenet findes ved at kombinere formlerne for stofmængde med pufferligningen.

   Man har pufferligningen: pH = pK_s + log(n_B/n_S). Hvor

      pK_s = 7,21 er minus logaritmen til syrestyrkekonstanten for H₂PO₄^-,

      n_B er antal mol HPO₄^2- og

      n_S er antal mol H₂PO₄^-

   Der gælder videre at: n_B = n_NaOH og n_S = n_S,start - n_NaOH. Her er

      n_S,0 antal mol H₂PO₄^- fra start.

   Dette findes ved formlen: n_S,0 = m_S,0/M_S, hvor

      m_S,0 = 340 mg er massen af KH₂PO₄ fra start og

      M_S = 136,086 g·mol^-1 er molmassen af KH₂PO₄.

   Man har nu, idet man ved at pH = 8,0 i opløsningen:

   8,0 = 7,21 + log(n_NaOH/((0,340g/136,086 g·mol^-1) - n_NaOH)).

   Man har tilsidst: n_NaOH = C_NaOH·V_NaOH = (1 M)·V_NaOH, hvor V_NaOH er rumfanget af tilsat NaOH-opløsning. Dette giver for V_NaOH:

   V_NaOH = [(0,34 g)/(136,086 g·mol^-1)]·[(10^8,0-7,21)/(1+10^8,0-7,21)]/(1 M) = 0,00215 L.

   Dvs. man skal tilsætte 2,2 mL NaOH-opløsning for at få en pH-værdi i pufferen på 8,0.

Svar på opgave 4: Et vigtigt råstof til gummifremstilling

1. Der er tale om en eliminations-reaktion, da der der fraspaltes et mindre molekyle fra 2-chlor-2-methylpropan og dannes en dobbeltbinding.

   

2. Man slår S^o op for de tre stoffer i reaktionen:

      (CH₃)₃CCl: 322,3 J·mol^-1·K^-1

      (CH₃)₂CCH₂: 293,6 J·mol^-1·K^-1

      HCl: 186,9 J·mol^-1·K^-1

   Man finder ΔS^o (ændringen i standard molær entropi) for reaktionen mod høre, ved at summere entropierne for stofferne på højre side af reaktionspilen og fratrække entropien af stoffet på venstre:

   ΔS^o = (293,6 + 186,9 - 322,3) J·mol^-1·K^-1 = 158,2 J·mol^-1·K^-1

   Kommentar: for gasfase-reaktioner gælder, at hvis der dannes flere molekyler ved reaktionen end, der var i forvejen, så stiger entropien. Dette passer med, at ΔS^o er positiv i dette tilfælde.

3. Man kender ikke totaltrykket, men det antages, at reaktionsblandingen er en ideal gas, hvorved K er uafhængig af totaltrykket.

   Man skal bruge van't Hoff ligning for at finde K ved 250 °C:

   ln(K) = (-ΔH^o/R)·(1/T) + ΔS^o/R. Her gælder, at

   ΔH^o er ændringen i standard molær enthalpi for reaktionen mod højre. ΔS^o er den samme som før.

   Man slår H^o op for de tre stoffer i reaktionen:

      (CH₃)₃CCl: -182,2 kJ·mol^-1

      (CH₃)₂CCH₂: -17,9 kJ·mol^-1

      HCl: -92,3 kJ·mol^-1

   Dette giver: ΔH^o = (-17,9 + (-92,3) - (-182,2)) kJ·mol^-1 = 72000 J·mol^-1. Desuden har man at:

      T = 273,15 + 250 K = 523,15 K og

      R = 8,314 J·mol^-1·K^-1.

   Værdierne for ΔH^o, ΔS^o, R og T indsættes og man får:

   ln(K) = (-72000 J·mol^-1)/[(8,314 J·mol^-1·K^-1)·(523,15 K)] + (158,2 J·mol^-1·K^-1)/(8,314 J·mol^-1·K^-1) ⇒ ln(K) = 2,4744.

   Dette giver, at ligevægtskonstanten er lig med 10^2,4744 bar = 11,8 bar

   Enheden findes fra massevirkningsloven: K = p_(CH3)2CCH2·p_HCl/p_(CH3)3CCl, hvor K har enheden bar²/bar = bar.

4. Reaktionen forløber spontant mod højre, når ΔG^o < 0. Der gælder formlen: ΔG^o = ΔH^o - T·ΔS^o for sammenhængen mellem ΔG^o og den absolutte temperatur.

   Dvs. man skal løse uligheden ΔH^o - T·ΔS^o < 0 med hensyn til T.

   Her i indsætte de værdier, der blev fundet ovenfor for temperaturen 25 °C:

   72000 J·mol^-1 - T·(158,2 J·mol^-1·K^-1) < 0 ⇒ T > (72000 J·mol^-1)/(158,2 J·mol^-1·K^-1) ⇒

   T > 455,1 K.

   Dvs. temperaturen skal være over (455,1 - 273,15) °C = 182,0 °C for, at reaktionen mod højre kan forløbe spontant i standardtilstanden, dvs. ved totaltrykket 1,00 bar.

5. Man har følgende partialtryk ved ligevægt:

      (CH₃)₃CCl ⇌ (CH₃)₂CCH₂ + HCl

          (p₀ - p)                 p               p

   Her er p₀ start-partialtrykket for (CH₃)₃CCl og p er ligevægts-partialtrykket for både (CH₃)₂CCH₂ og HCl. Ved konstant rumfang og temperatur gælder, at partialtryk er proportionalt med stofmængde.

   Dermed er (p₀ - p) ligevægtstrykket af (CH₃)₃CCl, da ændringen i stofmængden af (CH₃)₃CCl er lig med den dannede stofmængde af hvert produkt. Da rumfanget er konstant er trykket af hvert stof (stoffernes partialtryk) proportional med deres stofmængde.

   Man skal finde [(p₀ - p)/p₀]·100 %. Der gælder i følge massevirkningsloven:

   p²/(p₀ - p) = K. Man kender K som er 11,8 bar ved 250 °C.

   Man beregner p₀ ved hjælp af idealgasligningen: p₀·V = n₀·R·T = (m₀/M)·R·T ⇒

   p₀ = m₀·R·T/(M·V). Her er

      m₀ = 2,05 g lig med startmassen af (CH₃)₃CCl,

      R = 0,08314 bar·L·mol^-1·K^-1 er gaskonstanten,

      M = 92,57 g·mol^-1 er molmassen af (CH₃)₃CCl,

      T = (250 + 273,15) K = 523,15 K er Kelvin-temperaturen for reaktionen og

      V = 2,5 L er reaktionsbeholderens rumfang.

   Dette giver: p₀ = (2,05 g)·(0,08314 bar·L·mol^-1·K^-1)·(523,15 K)/[(92,57 g·mol^-1)·(2,5 L)] = 0,3853 bar.

   Dette indsættes i massevirkningsudtrykket for at finde p ved ligevægt:

   p²/(p₀ - p) = K ⇒ p²/(0,3853 bar - p) = 11,8 bar ⇒ p = 0,3735 bar.

   Den procentdel af (CH₃)₃CCl, der er tilbage ved ligevægt er dermed [(0,3853 bar - 0,3735 bar)/(0,3735 bar)]·100 % = 3,1 %