Svar på opgave 1: Triclosan

1. Kurven i et Bjerrumdiagram (for en monoprot syre) viser opløsningens sammensætning af det korresponderende syre-basepar. På skalaen til venstre kan man aflæse andelen af syre (syrebrøken) ved en bestemt pH-værdi. Andelen af korresponderende base (basebrøken) er 1 minus andelen af syre. (Det bemærkes at for en monoprot syre er der ikke forskel på molbrøk og syrebrøk hhv. basebrøk).

   

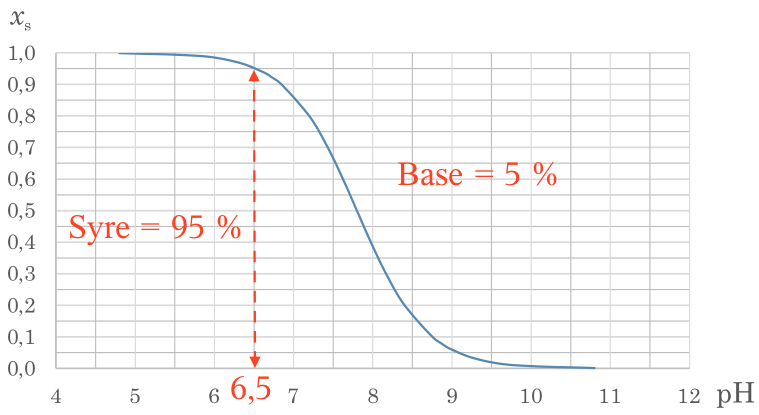
   Som vist på billedet ovenfor aflæses procentdelen af triclosan på syreform til 95 % og dermed er procentdelen af triclosan på baseform: 100 % - 95 % = 5 %

2. Man skal beregne den fortynding, der sker af stamopløsningen. Når 2 mL forøges til 100 mL, sker der en 100:2 = 50 gange fortynding. Dvs. den nye blanding er 50 gange tyndere end stamopløsningen.

   Da stamopløsningen har en koncentration på 200 mg/L er den nye blandings koncentration: (200 mg/L):50 = 4 mg/L

3. I spektrofotometri gælder, at ved lave koncentrationer af det farvede stof vil der være en linær sammenhæng mellem stoffets koncetration og dets absorbans.

   

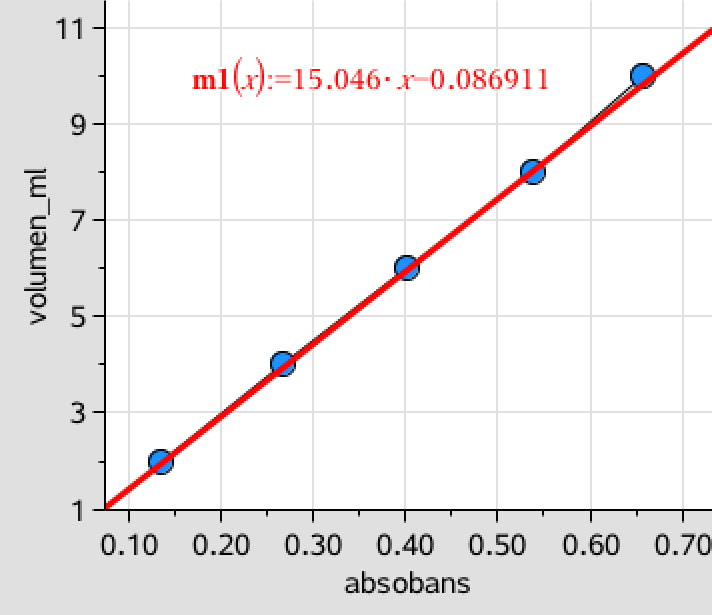
   Figuren ovenfor er lavet i Ti-Nspire. Det ses, at der med god tilnærmelse gælder en lineær sammenhæng for de målte værdier af absorbans og volumen i opgaven. Ud fra de fire laveste værdier er der lavet en retlinet tendenslinje vist med rødt.

   Denne giver sammenhængen: volumen i mL = 15,046·absorbans - 0,08691.

   For en absorbans på 0,281 for man et volumen på: (15,046·0,281 - 0,08691) mL = 4,141 mL.

   4,141 mL svarer til en fortynding af stamopløsningen på 100:4,141 gange = 24,15 gange.

   Dvs. koncentrationen af triclosan i den målte opløsning er (200 mg/L):24,15 = 8,28 mg/L

   Dette skal sammenlignes med et maksimalt tilladt vægtindhold af triclosan på 0,3 % i 0,254 g deodorant. Dette svarer til 0,003·0,254 g = 0,000762 g = 0,762 mg. Hvis denne mængde var opløst i 100 mL som prøven, ville koncentration af triclosan være 0,762 mg/(100 mL) = 7,72 mg/L.

   Man får, at den maksimalt tilladte koncentration af triclosan i prøven er 7,62 mg/L, mens den rigtige koncentration er 8,28 mg/L. Dermed er den maksimalt tilladte koncentration af triclosan overskredet.

Svar på opgave 2: Pentobarbital - et etisk dilemma

1. Stofmængdekoncetrationen af pentobarbital (p) er C_p = n_p/V = [m_p/M_p]/V =

   [(50 mg)/(248,26 g/mol)]/(1,00 mL) =

   [(50·10^-3 g)/(248,26 g/mol)]/(1,00·10^-3 L) =

   (50/248,26) mol/L = 0,201 M

2. Man bruger formlen for pH af svag base:

   pH = 14 - pOH = 14 - 0,5·(pK_b - log(C_b)) =

   14 - 0,5·(-log(K_b) - log(0,201)) =

   14 - 0,5·(-log(1,29·10^-6) - log(0,201)) = 14 - 3,29 = 10,7

   Dvs. pH i den vandige opløsning af pentobarbitals korresponderende base er 10,7

3. I begge reaktioner reagerer stofferne i forholdet 1:1. Det betyder at antal mol dannet pentabarbital er lig med antal mol af det stof, der er i underskud i første reaktion samt at stoffet i underskud er det stof af A og B, som har den mindste stofmængde.

   Man får, at stofmængden af A er (15 g)/(188,22 g/mol) = 0,07969 mol.

   Stofmængden af B er (12 mL)·(1,23 g/mL)/(151,04 g/mol) = 0,0977 mol.

   Da stof A findes i den mindste stofmængde kan produktet petobarbital højst have stofmængden 0,07969 mol. Ganges dette med molmassen for pentobarbital får man at den maksimale masse af pentobarbital som kan dannes er (0,07969 mol)·(226,29 g/mol) = 18,03 g

4. Man får at vide, at det undersøgte stof er en alkylbromid, dvs. stoffet har formlen C_nH_2n+1Br.

   

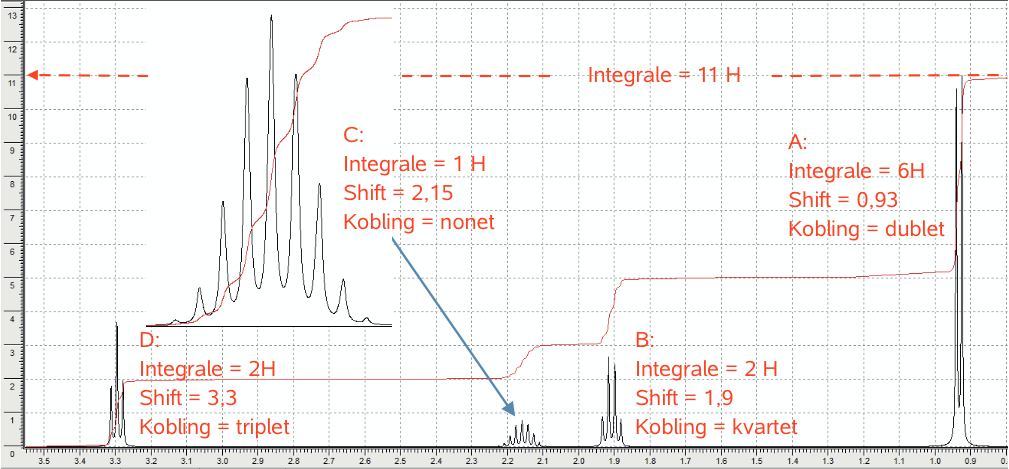
   Den røde integralkurve når op til 11, dvs. der er 11 H og dermed finder man n i ovenstående ligning: 2n + 1 = 11 ⇒ n = 5, dvs. der er 5 C-atomer.

   Man ser nu på det top, der har det højeste shift på ovenstående figur. Det er D. Toppen D har integralet 2 og den stammer derfor fra 2 H, der sidder på samme C-atom. Et shift på 3,3 kan kun forklares ved, at der også sidder et Br-atom på det pågældende C. Eletrofile grupper trækker shiftet op. Det C-atom, som de to H-atomer og Br-atomert sidder på må være endestillet, da der kun er en binding ledig på C-atomet.

   Man ser nu på den største top (A), der har et shift på 0,93. Denne top stammer fra 6 H, som det fremgår af integralkurven. Shiftet viser, at de stammer fra -CH₃ grupper, dvs. at de sidder på endestillede C-atomer. Det at der er 6 H, betyder at der må være to -CH₃ grupper, der er lige langt fra Br-atomet, så de får præcis samme shift. Dubletten viser, at der er 1 H på det C-atom, som de to -CH₃ grupper er bundet til.

   Nonetten med integralet 1 er et H der er sider på et C-atom der er bundet til tre C.-atomer med tilsammen 8 H-atomer (disse kan ikke sidde på mindre end 3 C-atomer.) Det C som er bundet til dette H-atom, er dermed det. C som sidder i forgreningen mellem de to -CH₃ grupper.

   

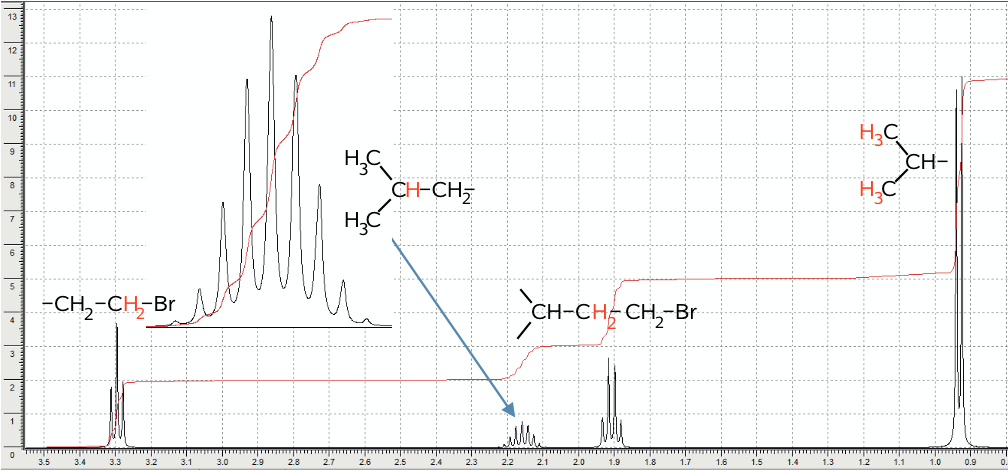
   De fire toppe er dermed forklaret og placeringen af H, C og Br vist på ovenstående billede.

   Det færdige stof bliver (CH₃)₂-CH-CH₂-CH₂Br, 1-brom-3,3-dimetylbutan.

Svar på opgave 3: Citalopram - et antidepressivt middel

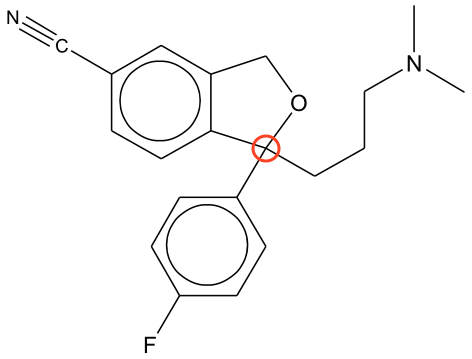
1. Stoffet har netop eet asymmetrisk kulstofatom og findes dermed i to spejlbilledisomere former. Det asymmetrsike kulstofatom er markeret med en rød ring på billedet nedenunder.

   

2. Stofferne B og C affarver bromvand ved addition til en dobbeltbinding.

3. Stof A indeholder som det eneste en C=O binding, der giver et absorbtionsbånd ved 1700 til 1800 cm^-1.

   Stof B indeholder som det eneste en O-H bindíng, der giver et absorbtionsbånd ved 3200-3525 cm^-1.

   C=C (alifatisk eller aromatisk) og C≡N er fælles

   Har man et stof og ved man, at det er enten A, B eller C, burde man kunne afgøre, hvilket det er, ud fra C=0 eller O-H.

4. Det ses, at jo mindre D, jo større vandopløselighed.

   Citalopram er overvejende hydrofob. Det indeholder ganske vist fire hydrofile grupper: -O- (ether), -F (flour), -N-- (tertiær amin) og C≡N (nitril), men disse opvejes af 5 kustofatomer pr. hydrofil gruppe. Derfor er citalopram overvejende i den organiske fase ved høje pH-værdier, hvor den tertiære amin findes på sin (ikke-ioniske) basiske form. D vokser derfor med stigende pH.

   Ved lave pH-værdier har den tertiære amin optaget et H⁺ og optræder som ammonium-ion. Denne ion er kun lidt opløselig i organisk opløsningsmiddel og D bliver derfor mindre ved lave pH-værdier,

Svar på opgave 4: Sulfurylchlorid - en kilde til dichlor

1. Trykket stiger fordi antallet af molekyler stiger.

2. ΔS^o = ΔS^o(SO₂) + ΔS^o(CL₂) - ΔS^o(SO₂CL₂) = 248,23 J/(mol·K) + 223,08 J/(mol·K) - 311,94 J/(mol·K) = 159,37 J/(mol·K)

   Entropien stiger, hvilket passer med, at der bliver flere molekyler.

3. Man bruger van't Hoff ligningen for at finde ligevægtskonstanten ved 100 ^oC.

   Man kender ikke totaltrykket, men antager at reaktionsblandingen er en idealgas, hvorved ligevægts­konstanten er tryk­uafhængig.

   ln(K_p) = -ΔH^o/(R·T) + ΔS^o/R.

   ΔH^o = ΔH^o(SO₂) + ΔH^o(Cl₂) - ΔH^o(SO₂Cl₂) = [-296,81 + 0 - (-364)] kJ/mol = 67,19 kJ/mol = 67190 J/mol.

   Dette giver:

   ln(K_p) = -(67190 J/mol)/(8,314 J/(mol·K))·(1/(273,15+100,0)K) + (159,37 J/(mol·K))/(8,314 J/(mol·K)) = -2,489 ⇒

   K_p = e^-2,489 = 0,0830 bar

4. For at finde trykket bruger man idealgasligningen på SO₂Cl₂ i beholderen.

   p = (n·R·T)/V = (0,0321 mol·[0,08314 bar·L/(mol·K)]·373 K)/(2 L) = 0,498 bar

   Ved ligevægt gælder: P(SO₂)·P(Cl₂)/P(SO₂Cl₂) = 0,083 bar.

   P(SO₂Cl₂,ligevægt) = 0,498 bar - P(Cl₂,ligevægt)

   P(SO₂,ligevægt) = P(Cl₂,ligevægt)

   Dette giver ligningen for P(Cl₂,ligevægt), som her forkortes x:

   x²/(0,498 bar - x) = 0,0823 bar ⇒ x = 0,0165 bar.

   Det vil sige, at partialtrykket af Cl₂ ved ligevægt er 0,0165 bar

5. Man skal løse ligningen P(SO₂Cl₂) + P(SO₂) + P(Cl₂) = 0,538 bar med hensyn til P(SO₂Cl₂).

   Der gælder, at P(SO₂Cl₂) = 0,498 bar - P(Cl₂) og P(SO₂) = P(Cl₂).

   Sættes P(Cl₂) = x fås: (0,498 bar - x) + 2x = 0,538 bar ⇒ x = 0,04 bar.

   Dvs. P(SO₂Cl₂) = 0,498 bar - 0,04 bar = 0,458 bar.

   Aktiveringsenergien findes ved hjælp af Arrhenius ligning:

   ln(k₂/k₁) = -(E_a/R)·(1/T₂ - 1/T₁) ⇒

   ln(0,014/0,001396) = -[E_a/(8,314 J/(mol·K))]·[1/((273 + 112) K) - 1/((273 + 100) K)] ⇒

   E_a = (2,3055·8,314/0,000084) J/mol = 229,4 J/mol