Svar på opgave 1: Coltan

1. Nb og Fe reduceres, idet deres oxidationstrin mindskes. Al oxideres, da dets oxidationstrin stiger.

   (At der her er mere end et grundstof, der reduceres skyldes, at det er to redoxprocesser, der er lagt sammen. Derfor kan reaktionsskemaet også afstemmes på flere måder.)

2. Nb₂O₅ (niobit) reagerer med Al i forholdet 1 : 4, dvs. der forbruges 4 mol Al hver gang, der omdannes 1 mol niobit.

   For at beregne antal mol niobit, skal man kende stoffets molmasse. Den er 2·92,9 g/mol + 5·16,0 g/mol = 265,8 g/mol.

   Antal mol omdannet niobit (n_niobit) = massen af niobit (m_niobit) divideret molmassen (M_niobit):

   n_niobit = m_niobit/M_niobit = (33.000.000 g)/(265,8 g/mol) = 124.153 mol.

   Dette giver for stofmængden af omdannet aluminium: n_Al = 4·124.153 mol = 496.612 mol.

   Dette skal ganges med aluminiums molmasse, som er 27 g/mol, dvs: Masse af aluminium = (496.612 mol)·(27 g/mol) = 13,4 mio. g = 13,4 tons

3. Massen af HF i 1 L må ikke være større end (42 %)·(1,11 g/mL)·(1 L) = 0,42·1,11 g/(10^-3 L)·(1 L) = 0,42·1,11·10³ g = 466,2 g.

   Massen af HF i 1 L flussyreopløsning er den molære koncentration af HF gange molmassen af HF (M_HF). Det forudsættes i øvrigt, at opløsningen ikke indeholder andre syrer end HF.

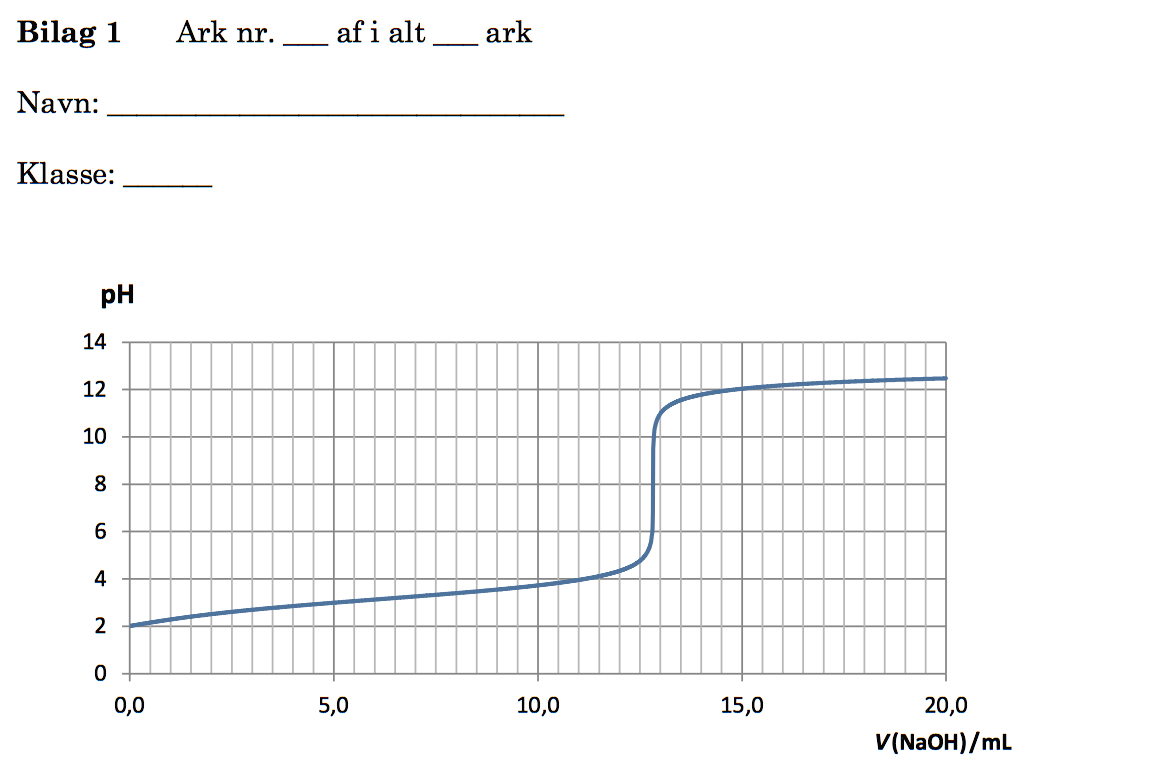
   For at bestemme den molære koncentration titrerer man en fortyndet opløsning. Fortyndingsgraden er: (50 mL)/(0,4 mL) = 125 gange.

   Den del af fortydingen, der titreres, kaldes titrator. Dens rumfang er 10,00 mL (V_titrator), og man skal finde det antal mol HF, der er i væsken før titrering. Dette er lig med antal mol NaOH tilsat ved omslag, idet HF og NaOH reagerer 1:1.

   Antal mol tilsat NaOH ved omslag er lig med rumfang af NaOH-opløsning tilsat ved omslag (V_omslag) gange koncentrationen af NaOH (c_NaOH) i titrervæsken.

   

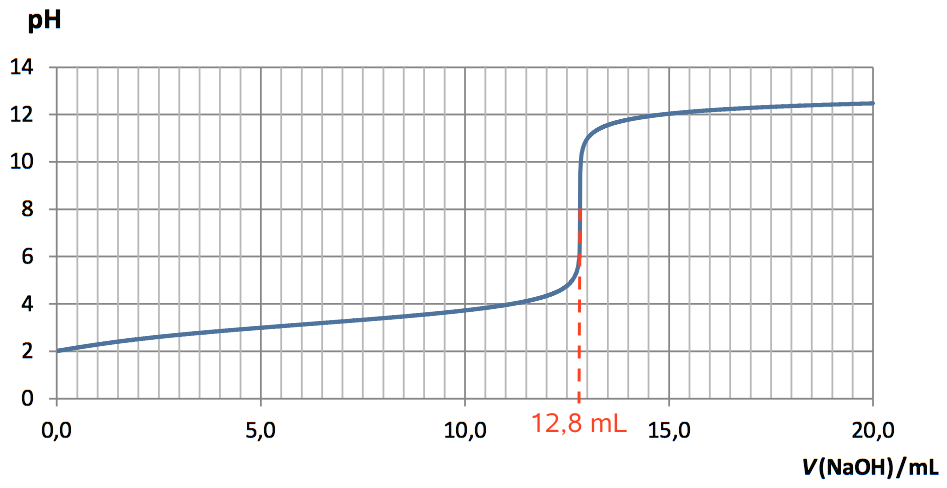
   V_omslag aflæses af titrerkurven til 12,8 mL som vist ovenfor.

   Tilsammen får man, at massen af HF pr. liter af den oprindelige opløsning er:

   [(50 mL)/(0,40 mL)]·[c_NaOH·V_omslag/V_titrator]·M_HF

   [(50 mL)/(0,40 mL)]·[(0,117 mol/L)·(12,8 mL)/(10,00 mL)]·(20,0 g/mol) =

   [50/0,40]·[0,117·12,8/10,00]·20,0 (mL/mL)·(mol/L)·(mL)·(1/mL)·(g/mol) =

   125·[0,117·12,8/10,00]·20,0 g/L = 374,4 g/L

   Dvs. en liter af flussyreopløsningen indeholder 374,4 g HF. Da det er mindre end de 466,2 g, der var de maksimalt tilladte, kan man godt bruge flussyreopløsningen.

Svar på opgave 2: Levulinsyre - et grønt råstof

1. Det systematiske navn for levulinsyre er 4-oxopentansyre

   Forklaring: den funktionelle gruppe i stoffet, som har højest prioritet, er carboxylsyre. Derudover er der en carbonylgruppe. Der er ikke andre funktionelle grupper eller sidekæder.

   Den længste kulstofkæde, som indeholder carboxylsyregruppen er pentan. Dermed ender stoffets navn på "pentansyre".

   En carbonyl-gruppe, der har lav prioritet, kaldes oxo-. (Hvis C=O har højest prioritet, kaldes stoffet en aldehyl eller en keton). Carbonyl-gruppens placering i kulstofhæden regnes fra C'et i -COOH. Det ses, at C=O sidder på kulstofatom nummer 4, og dermed bliver stoffets navn det nævnte.

2. pK_s = 4,78, så man bruger formlen for svag monoprot syre: pH = 0,5·(pK_s - log(C_s)) = 0,5·(4,78 - log(0,102)) = 2,9

3. På nedenstående billede er reaktionerne markeret med tallene 1 og 2:

   

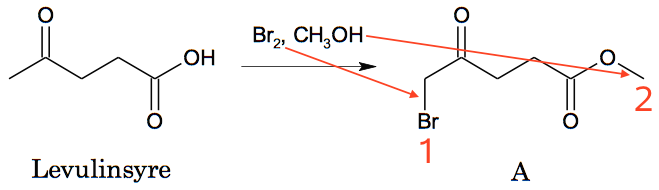
   Reaktion nr. 1 er en ketohalogenering (evt. en substitution, da H erstattes af Br). HBr bliver til overs.

   Reaktion nr. 2 er en esterdannelse, eller estersyntese (evt. en kondensation, da der fraspaltes vand). H₂O bliver til overs.

4. Et dobbeltbånd i IR-spektret omkring 3400 cm^-1 tyder på NH₂, dvs en primær amin.

   Inden man analyserer NMR-spektret, skal man bestemme molekyleformlen for stoffet ved hjælp af dets procentdele af indgående grundstoffer.

   Først skal man finde ud af, hvor mange mol C, der er i et mol af stoffet. Et mol af stoffer vejer 131,13 g og indeholder (45,8 %)·131,13 g C = 60,06 g. Et mol C vejer 12,0 g/mol, så 60,06 g C svarer til 60,06 g/(12,0 g/mol) = 5 mol.

   Samlet kan dette skrives: antal C-tomer i et B-molekyle = (45,8 %)·(131,13 g/mol)/(12,0 g/mol) = 0,458·131,13/12,0 = 5

   For de andre grundstoffer fås tilsvarende:

   Antal H-tomer i et B-molekyle = (9,62 %)·(131,13 g/mol)/(1,0 g/mol) = 0,0962·131,13/1,0 = 9

   Antal N-tomer i et B-molekyle = (10,68 %)·(131,13 g/mol)/(14,0 g/mol) = 0,1068·131,13/14,0 = 1

   Antal O-tomer i et B-molekyle = (36,6 %)·(131,13 g/mol)/(16,0 g/mol) = 0,366·131,13/16,0 = 3

   Dvs. molekyleformlen for stoffet B er C₅H₉NO₃

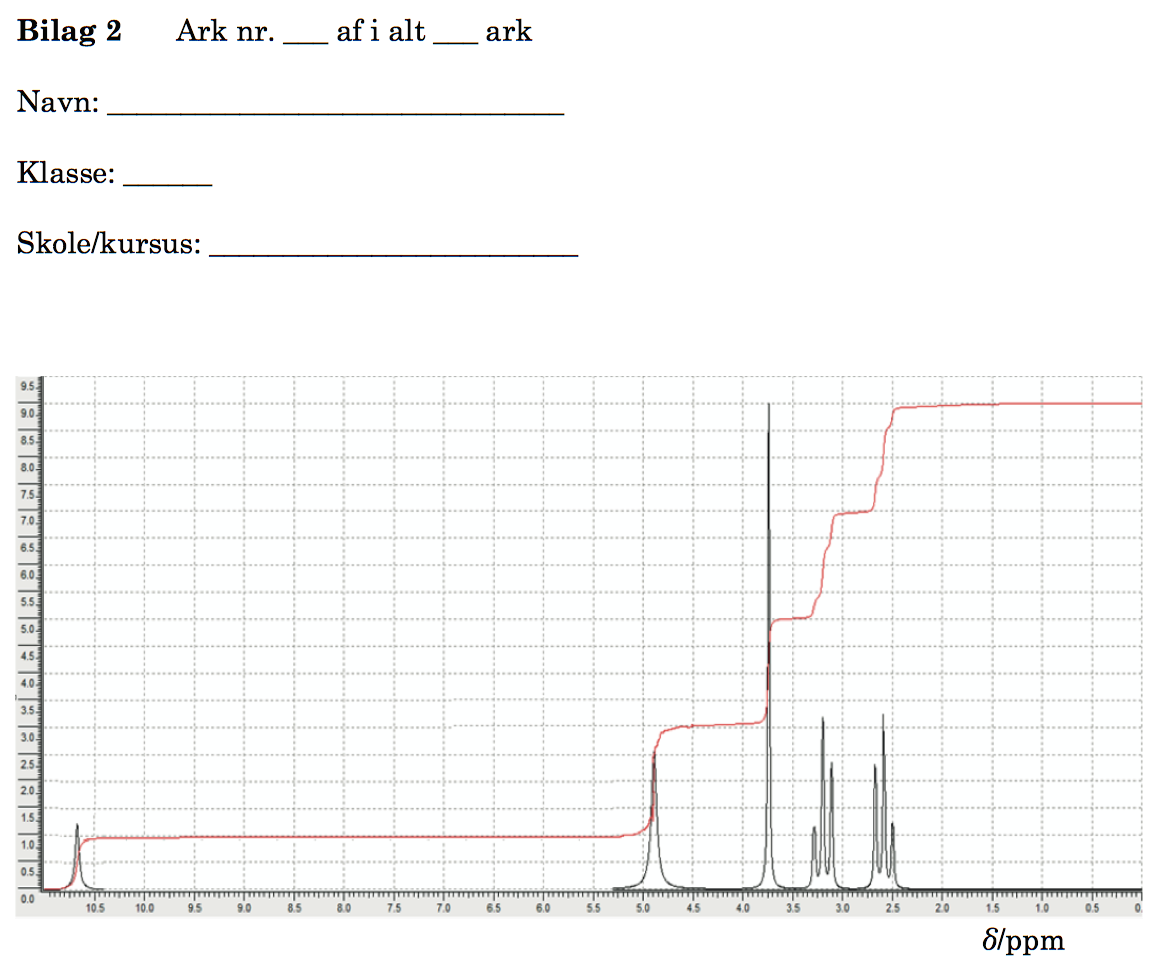
   På nedenstående billede er toppene i NMR-spektret nummererede fra 1 til 5:

   

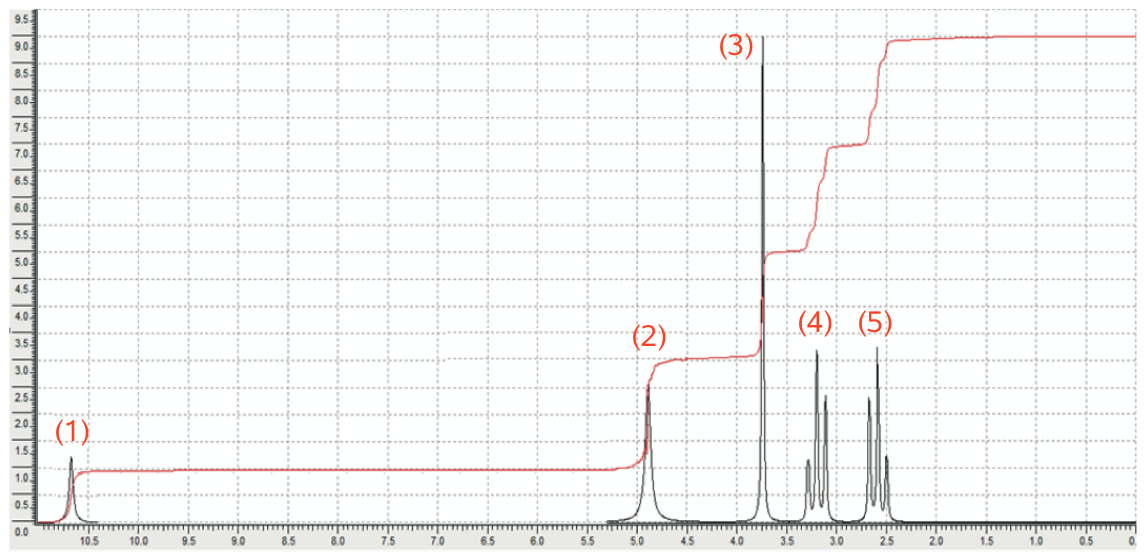
   Det ses, at det samlede integrale under toppene er 9 og dermed svarer et integrale på 1 til netop 1 H.

   Ud fra NMR-toppene forsøger man først at gøre rede for hvilke grupper, der indgår i molekylet.

   Toppen (1) er en bred singlet med et integrale på 1 og et skift på 10,7, hvilket tyder på COOH. At den har integralet 1 viser, at toppen stammer fra 1 H. At den er bred tyder på, at H er bundet til O eller N og ikke til C. At toppen er en singlet tyder på, at H enten er bundet til O eller N eller til et C, der ikke har nabo-C-atomer med H bundet til dem.

   Dermed har man fundet en COOH gruppe. Man ser nu på N-atomet:

   Toppen (2) er en bred singlet med integralet 2 og et skift på 5. Dette viser, at der er to H, som sandsynligvis sidder i en amin-gruppe: NH₂. Bevis: En bred singlet tyder som før nævnt på at H er bundet til N eller O, og O er her udelukket, fordi der ikke kan være 2 H bundet til samme O i et organisk stof.

   Dermed har man fundet en COOH gruppe og en NH₂-gruppe.

   Man ser nu på det sidste O for at finde ud hvilken funktionel gruppe, det tilhører. Her kan man udelukke -OH, idet dets H ville have givet en bred singlet med integralet 1 og et kemisk skift på 1-5. En sådan top findes ikke.

   O'et kan heller ikke stamme fra H-C=O, dvs. aldehyd, da det H, der indgår, ville have givet en top omkring 9-10. Det findes heller ikke. Den eneste top, der er i nærheden, tilhører som vist COOH.

   Tilbage er den mulighed, at O indgår i C=O (denne gruppe giver ikke nogen top, da den ikke indeholder H).

   Man har nu følgende grupper: COOH, NH₂ og C=O. Der resterer 3 C og 6 H. Disse atomer sidder i grupper af formen CH_n, hvor n = 0, 1, 2 eller 3.

   Det bemærkes, at alle de resterende toppe har integralet 2, og at de resterende grupper i stoffet alle må være på formen CH₂.

   Den mest enkle antagelse er nu, at stoffet B er 4-oxopentan, hvor NH₂ har substitueret et H på det yderste C regnet fra carboxylsyregruppen. Det stemmer med 1 COOH, 1 NH₂, 1 C=O og 3 CH₂.

   Man får dermed, at B er stoffet: 5-amin-4-oxopentansyre eller aminolevulinsyre og har strukturen som vist:

   

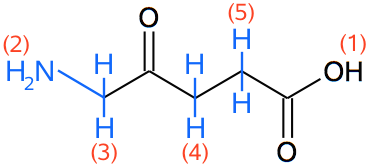
   (Det kemiske skift af toppene (3)-(5) på tegningen kan ikke bekræftes af tabellen, men deres splitmønster (n + 1) stemmer. 5-amin-3-oxopentansyre er også en mulighed, men mindre sandsynligt, da det kræver, at C=O skifter plads i kulstofkæden).

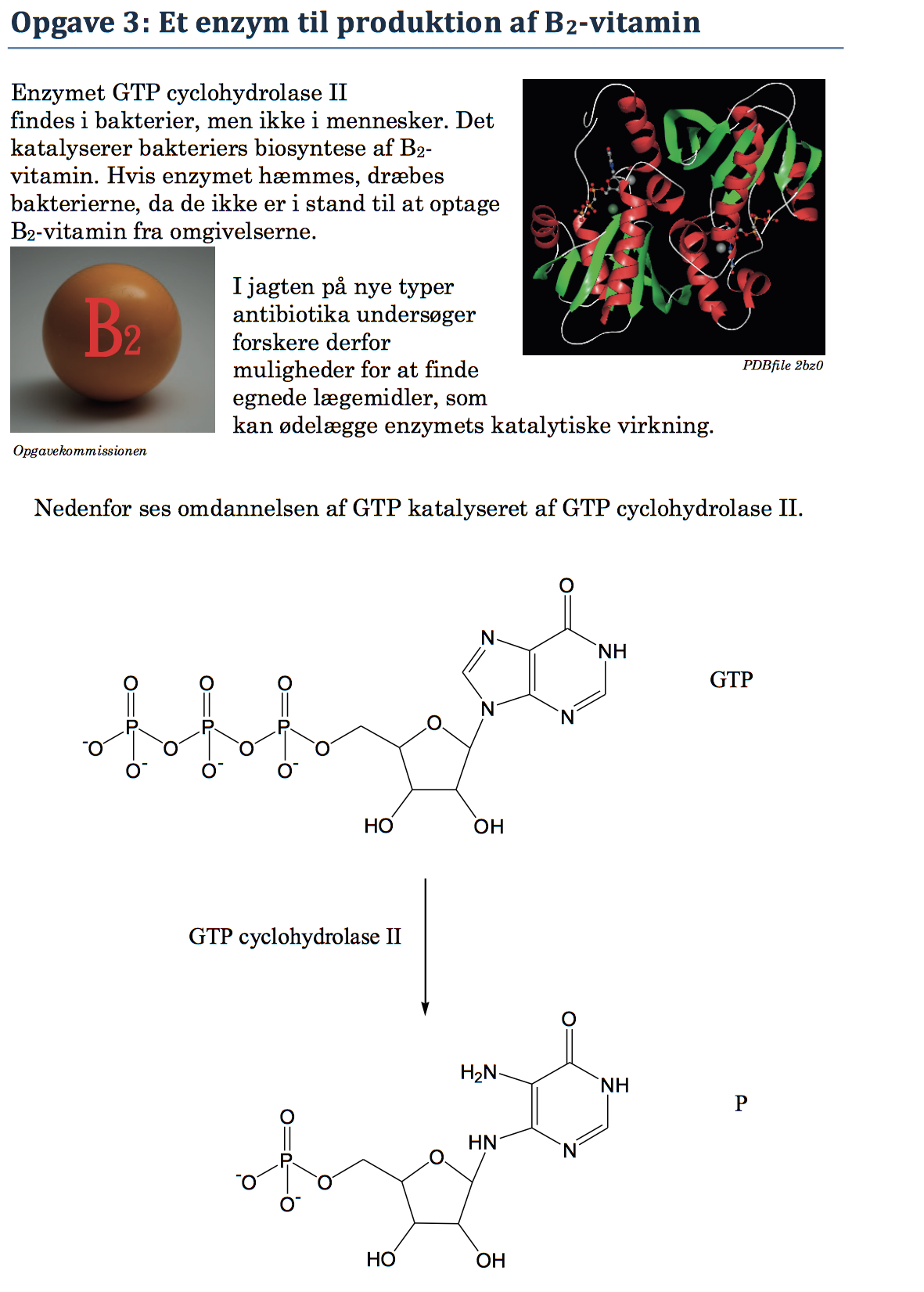
Svar på opgave 3: Et enzym til produktion af B₂-vitamin

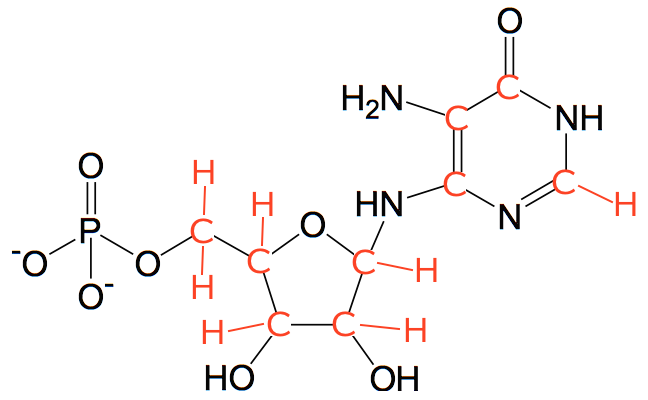
1. Der hvor streger på en stregformel mødes, skal der være et kustofatom. Hvert kulstofatom skal have fire bindinger. Normal udelades C-H bindinger på en stregtegning. H sættes derfor på C for at få fire bindinger til hvert C-atom.

   

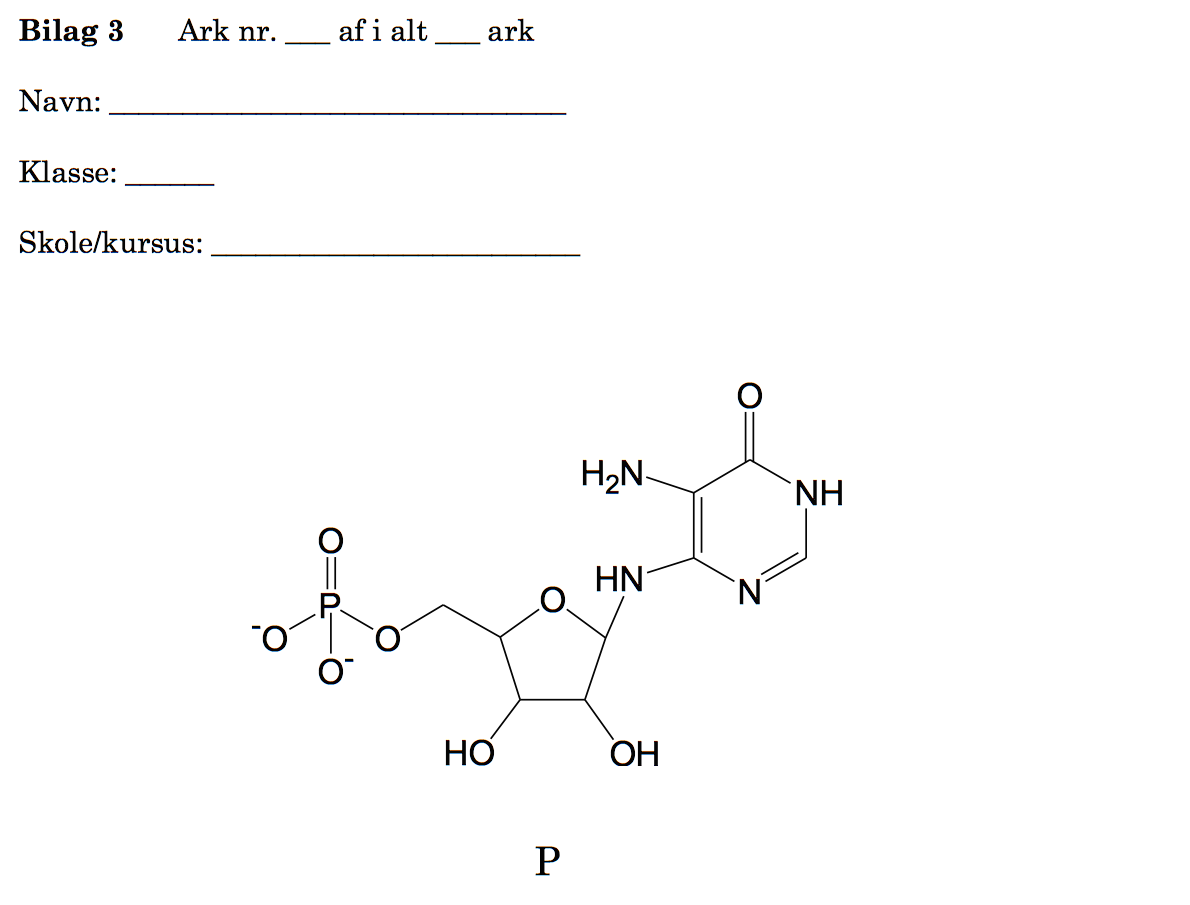
2. Konentrationen findes ved hjælp af Lambert-Beers lov:

   C = A/(ε·l), hvor C er koncentreationen af P, A er absorbansen, ε er den molære absorbtions­koefficient og l er kuvettebredden.

   Det giver koncentrationen: C = 0,285/(9,60·10³ M^-1·cm^-1·1,00 cm) = 2,97·10^-5 M

3. Det antaget i denne opgave at der gælder følgende sammenhæng mellem reaktionshastigheden v (dvs. omdannelses hastigheden af [GTP]) og koncentrationen af GTP:

   v = k·[GTP]ⁿ, hvor k er en konstant og n er et helt tal, som kaldes reaktions orden.

   Den rette linje i diagrammet har hældningen 0 og skærer andenaksen i v = 0,37 μM·s^-1.

   

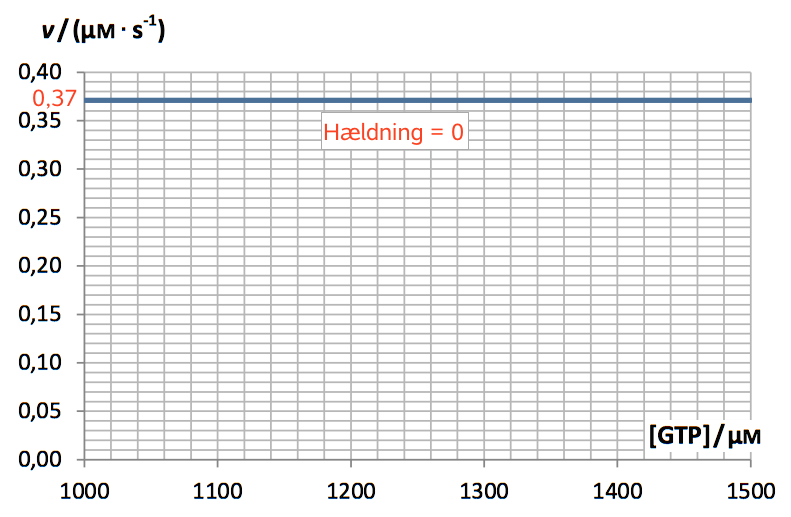
   Det viser at n = 0, fordi [GTP]⁰ = 1 og dermed forsvinder koncentrationen ud af formlen.

   Derefter bliver udtrykket: v = k, hvor k aflæses til 0,37 μM·s^-1

   Dvs. reaktionsordenen er 0 og hastighedskonstanten er 0,37 μM·s^-1 i det viste koncentrations­interval for GTP.

4. Ved koncentrationer af GTP på under 10^-7 M bliver nævneren: [GTP] + 4,30·10^-5 M ≈ 4,30·10^-5 M.

   Hele udtrykket bliver dermed tilnærmelsesvis: 3,71·10^-7 M·s^-1·[GTP]/(4,30·10^-5 M) = 8,628·10^-3 s^-1·[GTP], dvs. v = k·[GTP]¹ og dermed er reaktionen af første orden.

   Halveringskonstanten (T) for en førsteordensreaktion med hastighedskonstanten k er: T = ln(2)/k

   Det giver her: T = (ln(2)/0,008628) s = 80,3 s

Svar på opgave 4: Halogenpærer

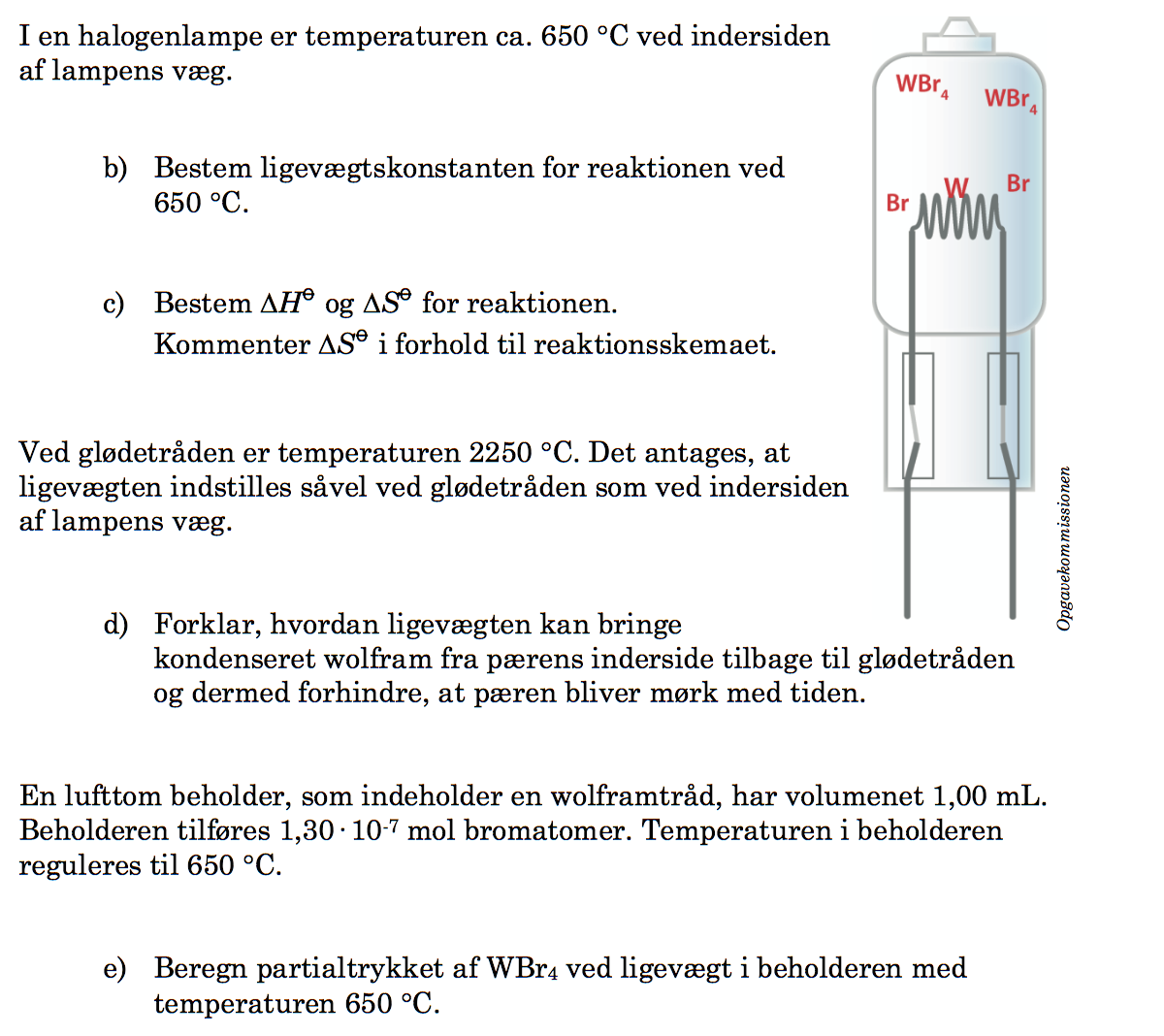
1. Ligevægtsudtrykket er p(WBr₄)/p(Br)⁴ = K

   hvor p(WBr₄) er partialtrykket af WBr₄(g) og p(Br)⁴ er partialtrykket af Br(g). W(s) indgår ikke fordi, det er et fast stof.

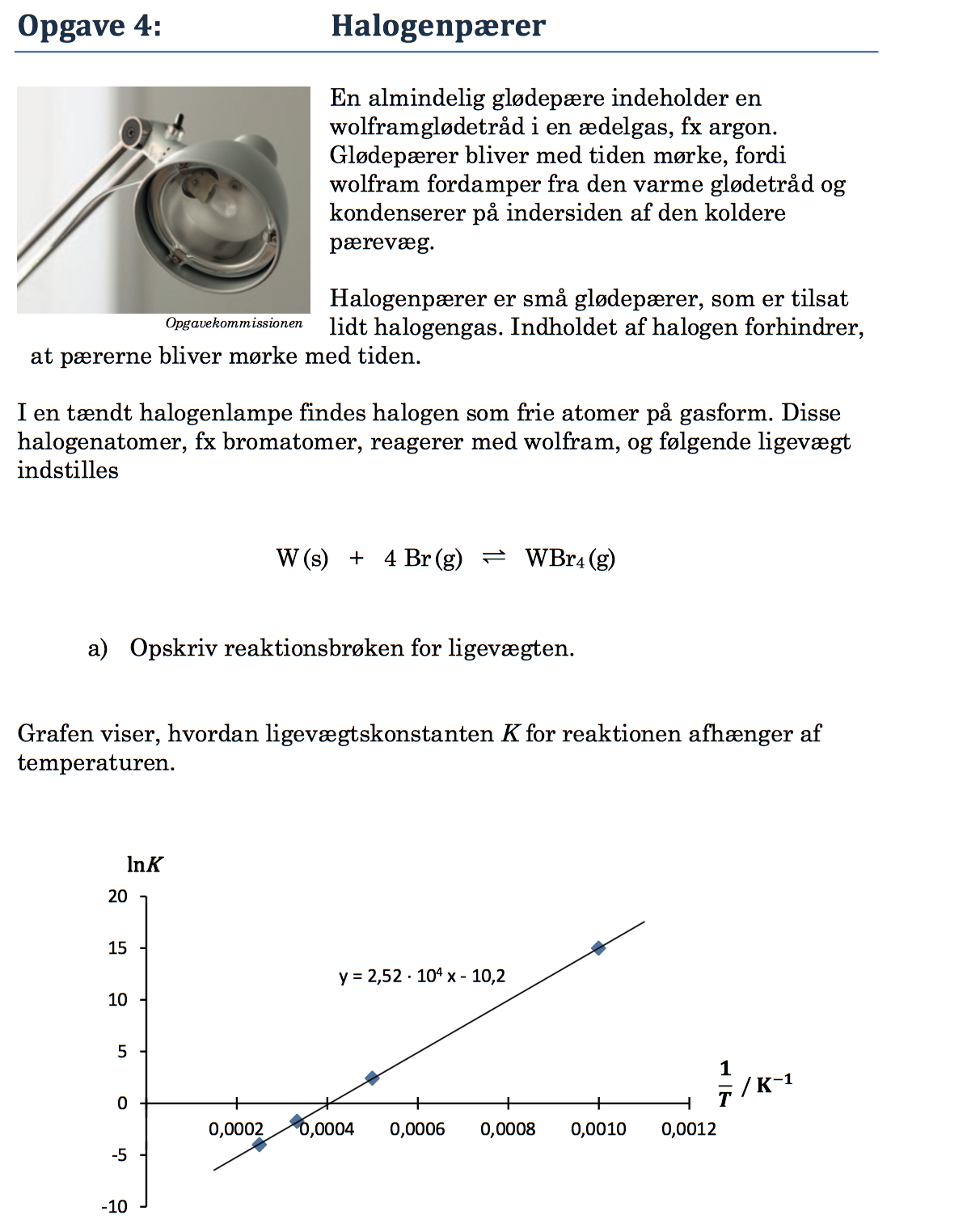
2. Af grafen ses at tendenslinjen har forskriften y = 2,52·10⁴·x - 10,2, hvilket vil sige

   ln(K) = (2,52·10⁴ K)/T - 10,2, hvor temperaturen har enheden Kelvin og K har enheden bar^-3. ln(K) skal være dimensionsløs.

   Man kender ikke totaltrykket, men hvis man antager, at reaktionsblandingen er en ideal gas, så kan man regne K for tryk­uafhængig.

   For T = 650 °C får man:

   ln(K) = (2,52·10⁴ K)/[(650 + 273) K] - 10,2 ⇒

   ln(K) = 2,52·10⁴/923 - 10,2 ⇒

   ln(K) = 17,1 ⇒

   K = e^17,1 bar^-3 = 2,67·10⁷ bar^-3

3. Grafen i figur 1 er et van't Hoff plot, dvs. et eksempel på følgende sammenhæng.

   ln(K) = (-ΔH^o/R)/T + ΔS^o/R

   Ved at sammenligne formlen for van't Hoff ligningen med tendenskurvens ligning, får man at

   -ΔH^o/R = 2,52·10⁴ J/mol ⇒

   -ΔH^o/(8,314 J/(mol·K)) = 2,52·10⁴ J/mol ⇒

   ΔH^o = -8,314 J/(mol·K)·2,52·10⁴ K ⇒

   ΔH^o = -209,5 kJ/mol

   Tilsvarende får man at ΔS^o/R = -10,2 ⇒

   ΔS^o = -8,314 J/(mol·K)·10,2 ⇒

   ΔS^o = -84,8 J/(mol·K)

   ΔS er negativ, dvs. at entropien mindskes. Det stemmer med, at der bliver færre gasmolekyler, når reaktionen forløber mod højre. (På den anden side bliver fast stof til gas, hvilket øger entropien, men åbenbart i mindre grad).

4. Man finder K_{2250 °C} og sammenligner den med K(650 °C).

   ln(K_{2250 °C}) = (2,52·10⁴ K)/[(2250 + 273) K] - 10,2 = −0,2208 ⇒

   ln(K_{2250 °C}) = −0,2208 ⇒

   K_{2250 °C} = e^−0,2208 = 0,8019

   Det ses at K_{2250 °C} er mindre end K_{650 °C}, dvs. at ligevægten er længere forskudt mod venstre ved glødetråden end ved indersiden af glasset og dermed har W større tendens til at afsættes på glødetråden end på glasset.

5. Ved ligevægt ved 650 °C gælder: p(WBr₄)/p(Br)⁴ = 2,67·10⁷ bar^-3

   For at bergne ligevægtspartilatrykkene skal man kende partialtrykket for Br ud fra starten. Dette gøres ved hjælp af idealgasligningen, idet man antager, at temperaturen er 650°C fra start: p(Br,start) = (1,30·10^-7 mol)·(8,314 J/(mol·K))·923K/(1,00 mL) = 9,976·10^-3 bar.

   Ved ligevægt gælder at: p(Br) = 9,976·10^-3 bar - 4·p(WBr₄), idet der forsvinder 4 Br-atomer for hver gang, der dannes et WBr-molekyle.

   Ved ligevægt får man således for partialtrykket af WBr₄:

   p(WBr₄)/[9,976·10^-3 bar - 4·p(WBr₄)] = 2,67·10⁷ bar^-3

   Dette løses i Ti-Nspire idet p = p(WBr₄):

   solve(p/(0.00997597-4*p)⁴)=2.67*10⁷,p) ▸ p=0.00177967 or p=0.00332941

   Af disse to resultater er kun p(WBr₄) = 0,001780 bar mulig, idet p(WBr₄) højst kan blive 0,00998/4 bar = 0,00249 bar, som er partialtrykket af WBr₄, hvis alt Br omdannes.

   Dvs. partialtrykket af WBr₄ ved 650 °C bliver 1,78·10^-3 bar