Svar på opgave 1: Benzylacetone

1. Stoffet B findes i to stereoisometriske former på grund af alken-dobbeltbindingen, hvor der sidder et H på hvert C-atom, og derudover er der to andre og indbyrdes forskellige grupper. Dette kaldes cis/trans-isomeri.

   På den ene form af stoffet sidder dobbeltbindingens to H'er på hver sin side af dobbeltbindingen. Dette er trans-formen, der er vist nedenunder.

   

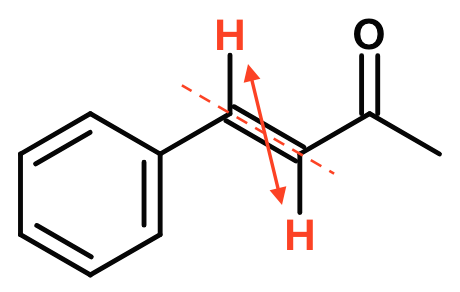
   På den anden form af stoffet sidder H'erne samme side af dobbeltbindingen. Dette er cis-formen, der er vist nedenunder.

   

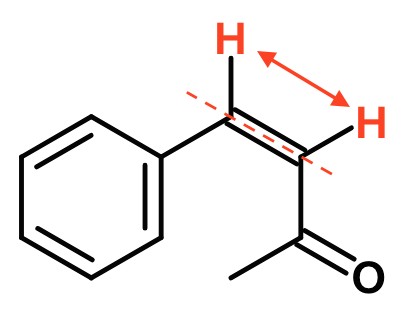
   Cis/trans-isomeri er et specialtilfælde af det mere generelle E/Z-isomeri, hvor der godt kan være 4 forskellige grupper bundet til de to C-atomer i dobbeltbindingen.

2. Den funktionelle gruppe i benzylacetone er en keton. Denne kan påvises i to trin:

   1. Først tilsættes 2,4-dinitrophenylhydrazin til noget af benzylacetonenen. Dette giver gult bundfald som tegn på at B enten indeholder en aldehyd eller en keton.

   2. For at afgøre hvilken en af dem, som det er, så tilsættes Fehlings reagens til en anden del af benzylacetonenen. Negativt testresultat, dvs udeblivelse af rødt bundfald, vil udelukke aldehyd og dermed sammen med den første prøve påvise en keton.

   Bemærkning: Man kan også bruge Tollens reagens i stedet for Fehlings reagens. Her vil positivt resultat være et sølvspejl på indersiden af reagensglasset eller et sort bundfald af fast sølv.

3. IR. Toppen ved 1700 cm^-1 svarer til strækningen i en C=O binding. Dette er vist nedenunder:

   

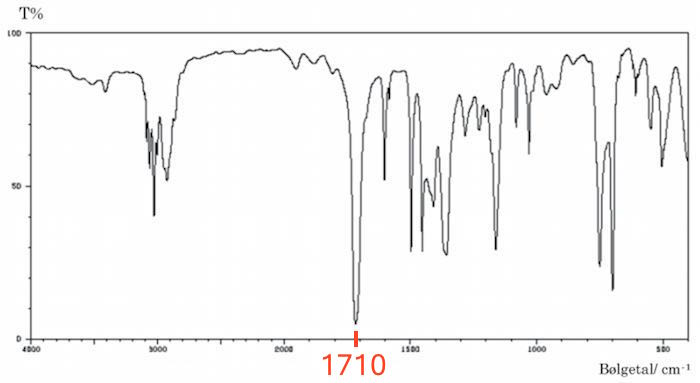
   Dette påviser ketonen, der ikke ville kunne ses på NMR-spektret, da der ikke er noget H, som er bundet til C=O gruppen.

   NMR. Det samlede intregrale er 12 (vist med rødt til højre). Dette vil sige, at integralet af en top er lig me antal H for topppen.

   Toppene er nummeret fra 1 til 4 (med blåt) og de tilsvarende H'er er nummeret på samme måde på strukturformlen for benzylacetone.

   

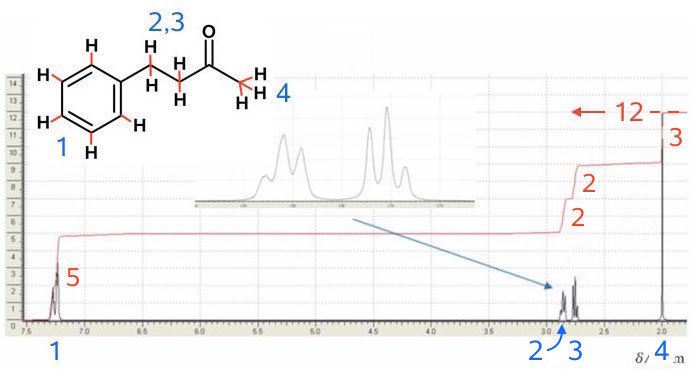
   Top 1: et kemisk skift på 7,3 og et integrale på 5. Det svarer til de 5 H'er i benzenringen. (Splittet er en blanding af en dublet og en triplet). Det kemiske skift på ca. 7 skyldes, at H'erne deshieldes af benzenringen.

   Top 2 og 3: to tripletter begge med 2 H og kemisk skift tæt på hinanden mellem 2,7 og 2,8. At splittet er en triplet passer n + 1 reglen, hvor n = 2 er antallet H'er på nabo C-atomet til hvert H-atom, giver dette en triplet som kobligsmønster.

   (På den forstørrede tegning ses, at de to toppe er asymmetriske, hvilket skyldes at de ligger tæt).

   Top 4: En singlet med 3 H og et kemisk skift 2. Dette svarer til H'erne på Ch₃ gruppen. Det er en singlet, fordi der ikke er nogen H på nabo C-atomet. Det lave kemiske skift skyædes at H'erne ikke deshieldes i særlig høj grad af O'et i C=O.

Svar på opgave 2: Glucose

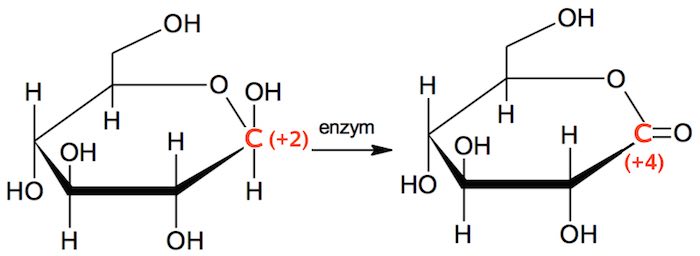
1. Der sker en oxidation

   Det fremgår af, at C'et til højre på ringstrukturen skifter oxidationstrin fra +2 til +4 som vist nedenunder.

   

2. Af grafen fra spørgsmålet fremgår det, at start-hastigheden (v₀) for rektionen med hensyn til glukose er proportional med start-koncentrationen af glukose (C_0,glukose).

   

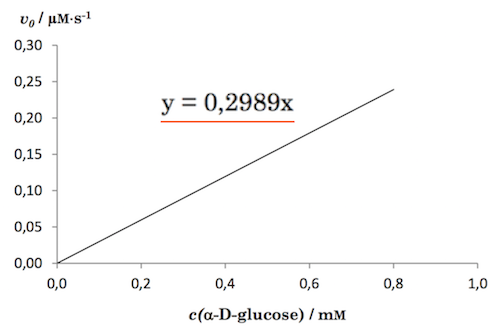
   Dvs. v₀ = k·C_0,glukose, der også kan skrives v₀ = k·(C_0,glukose)¹, hvor 1-tallet i eksponenten viser at reaktionen er af første orden med hensyn koncentrationen af glukose (i det mindste i det undersøgte interval: 0 < C_0,glukose < 1,0 mM).

3. Man beregner aktiveringsenergien (E_a) ved hjælp af Arrhenius-ligningen:

   k = A·exp(-E_a/(R·T)), hvor A er en konstant, R er gaskonstanten og T er Kelvin-temperaturen.

   Heraf kan kan E_a bestemmes som minus hældningen til grafen for ln(k) afbildet mod 1/T ganget med gaskonstanten. Dette er forudsat at grafen giver en ret linje.

   Dette gøres i dette tilfælde ved at lave lineær regression på sammenhængende værdier af 1/T og ln(k). For at gøre dette udfylder man først nedenstående tabel:

   

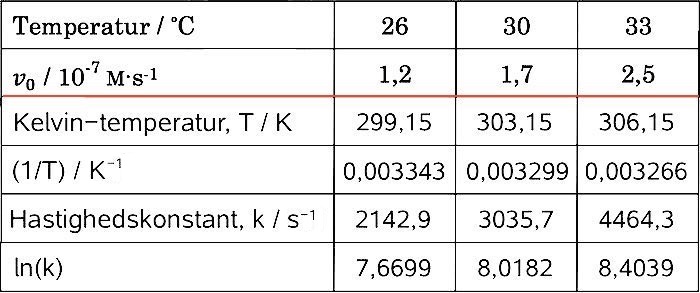
   Her er T = celciustemperatur + 273,15. Hastighedskonstanten k er beregnet ved hjælp af fomlen fra spørgsmål b):

   v₀ = k·C_0,glukose ⇒ k = v₀/C_0,glukose = v₀/(5,00·10^-5 M).

   (ln(k) er ubenævnt).

   Regressionen har en forklaringsgrad på 0,99, dvs. sammenhængen er tilnærmelsesvis lineær.

   Regressionsformlen er ln(k) = (-9502,5 K)·(1/T) + 39,414, hvor hældningen er -9502,5 K.

   Dette vil sige, at E_a = -(-9502,5 K)·R = -(-9502,5 K)·(8,314 J·mol^-1·K^-1) = 79,0 kJ·mol^-1

Svar på opgave 3: Eksploderende vandmeloner

1. Molekyleformlen er: C₁₂H₁₀ClN₃O

   (Først kommer C, så H og derefter resten af grundstofferne i alfabetisk orden).

2. Udbytteprocenten for dannelsen af forchlorfenuron er (100 %)·m_f/m_t, hvor

      m_f,fcf er massen af det faktiske udbytte af forchlorfenuron og

      m_t,fcf er massen af det teoretiske udbytte af forchlorfenuron.

   Man har for den teoretiske masse af forchlorfenuron: m_t,fcf = n_t,fcf·M_fcf, hvor

      n_t,fcf er den teoretisk størst dannede masse af forchlorfenuron og

      M_fcf er molmassen af forchlorfenuron.

   Man finder molmassen af forchlorfenuron:

   M_fcf = (12·12,011 + 10·1,008 + 35,45 + 3·14,007 + 16,000) g/mol = 247,68 g/mol.

   Anilin omdannes til forchlorfenuron i molforholdet 1:1, dvs. hvert anilin-molekyle, der bliver omdannet, bliver til et forchlorfenuron-molekyle.

   At anilin er begrænsende faktor betyder, at det er anilin, der føst bruges op (alle andre reaktanter er i overskud). Dermed kan alt anilin omdannes.

   Dette vil sige, at n_t,fcf = n_anilin = M_anilin/m_anilin, hvor

      n_anilin er stofmængden af anilin fra start,

      M_anilin er molmassen af anilin og

      m_anilin er massen af anilin fra start.

   Man har den teoretiske masse af forchlorfenuron: m_t,fcf = n_t,fcf · M_fcf = n_anilin · M_fcf =

   m_anilin · M_fcf / M_anilin = (100 g)·(247,68 g/mol)/(93,13 g/mol) = 265,95 g.

   Dvs. udbytteprocent = (100 %)·(147 g)/(265,95 g) = 55,3 %

3. For stofmængdekoncentrationen af forchlorfenuron (C_fcf) gælder formlen: C_fcf = n_fcf / V_opl = m_fcf / (M_fcf · V_opl), hvor

      V_opl er den færdige opløsnings rumfang = 10 L.

   Dette giver: C_fcf = m_fcf/(M_fcf·V_opl) =

   m_fcf/((247,68 g/mol)·(10 L)) = m_fcf · (4,0375·10^-4 mol·g^-1·L^-1)

   Man skal nu finde massen af forchlorfenuron, der tilsættes den færdige opløsning. Man ser af skemaet, at der udtages 75 mL af den oprindelige opløsning på 1,0 L, der indeholder 10 g forchlorfenuron.

   

   Dvs, disse 75 mL indeholder: (10 g forchlorfenuron)·(0,075 L)/(1,0 L) = 0,075 g forchlorfenuron.

   Dette skal tilsættes den færdige opløsning, og dermed er m_fcf = 0,075 g.

   Dvs. stofmængdekoncentrationen af forchlorfenuron i den færdige opløsning er

   (0,075 g)·(4,0375·10^-4 mol·g^-1·L^-1) = 3,028·10^-4 mol·L^-1 = 3,03·10^-4 M

Svar på opgave 4: Rhodamin B - et farvestof

1. Man skal fortynde 100 gange og ende med 0,1 L opløsning.

   Det kan gøres ved at udtage 1 ml med en 1,00 mL pipette af stamopløsningen på 8,00·10^-4 M.

   Denne 1,00 mL tilsættes en 100 mL målekolbe, som derefter fyldes til stregen med demineraliseret vand.

2. For ligevægtskonstaten (K) gælder: K = [Y]/[X].

   At Y-formen udgør 54,1 % af de to former vil sige, at [Y]/([X]+[Y]) = 0,54.

   Man dividerer med [X] i tæller og nævner og får: [Y]/([X]+[Y]) = 0,54 ⇒

   ([Y]/[X])/([X]/[X]+[Y]/[X]) = 0,54 ⇒ K/(1+K) = 0,54 ⇒ K = 1,18

   Dvs. ligevægtskonstanten for omdannelsen mellem X- og Y-formen er 1,18

3. Man skal bruge et van't Hoff plottet fra spørgsmålet:

   

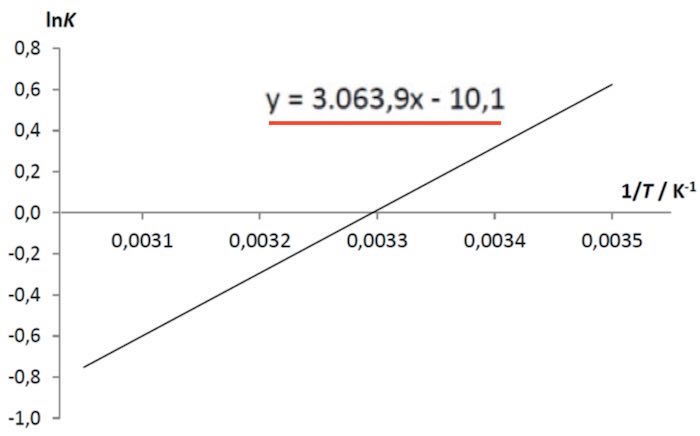
   Et van't Hoff plot følger formlen:

   ln(K) = (-ΔH^⊖/R)·(1/T) + ΔS^⊖/R.

   Plottet giver en ret linje med hældningen α og skæringen β med anden-aksen.

   Her er α = (-ΔH^⊖/R) og β = ΔS^⊖/R.

   Den rette linje har formen y = 3063,9·x - 10,1, dvs. α = 3063,9 K og β = -10,1.

   (At hældningen har enheden Kelvin følger, at x = 1/T og at hele højresiden skal være ubenævnt, da venstresiden (y) er ln(K), der er ubenævnt.)

   Dvs. ΔH^⊖ = - α·R = -(3063,9 K)·(8,314 J/(mol·K)) = -25,5 kJ/mol og

   ΔS^⊖ = β/R = -10,1·(8,314 J/(mol·K)) = -84,0

   Reaktionen (mod højre) er eksoterm, idet ΔH^⊖ er mindre end 0.

   Dvs. der udvikles varme ved reaktionen mod højre og forbruges varme ved reaktionen mod venstre.

   I følge le Chateliers princip betyder dette, at ved opvarming vil ligevægten forskydes mod venstre, da der derved forbruges varme.

4. Man bruger van't Hoff-ligningen til at finde ligevægtskonstanten ændring med temperaturen.

   Ligningen er: ln(K) = (3063,9 K)·(1/T) - 10,1. Det antages, at hverken ΔH^⊖ eller ΔS^⊖ ændres i temperatur-intervallet 25 °C til 42 °C.

   Kelvin-temperaturen ved 42°C er (42 + 273,15) K = 315,15 K. Dette giver følgende ligevægtskonstanten, K, ved temperaturen 42 °C:

   ln(K) = (3063,9 K)·(1/(315,15 K)) - 10,1 = -0,37796 ⇒ K = exp(-0,37796) = 0,6852.

   Man har nu følgende to ligninger med hensyn til koncentrationerne [X] og [Y]:

   K = [Y]/[X] = 0,6852 og samlet koncentration af X og Y = [X] + [Y] = 8,00·10^-6 M. Disse løses:

   [Y] = 0,6852·[X] ∧ [X] + [Y] = 8,00·10^-6 M ⇒

   [Y] = 0,6852·[X] ∧ (1 + 0,6852)·[X] = 8,00·10^-6 M ⇒

   [Y] = (0,6852/1,6852)·(8,00·10^-6 M) ∧ [X] = (8,00·10^-6/1,6852) M, der medfører, at

   [X] = 4,75 μM og [Y] = 3,25 μM ved 42 °C.

Svar på opgave 5: Barbitursyre og barbiturater

1. Man bruger formlen for pH for en middelstærk syre, da 0 < pK_s ≤ 4. Man har, at K_s = 10^-4 og den formelle koncentration af syre C_s = 0,0892 M. Dette giver:

   pH = - log(-K_s/2 + √[(K_s/2)² + K_s·C_s]) =

   pH = - log(-10^-4/2 + √[(10^-4/2)² + 10^-4·0,0892]) =

   pH = 2,53

   (Formlen for pH af svag syre giver 2,52 - ikke den store forskel!)

2. Barbitursyre findes næsten udelukkende som base ved pH = 7,2, da x_s (andelen af syre) er ca. lig med 0 ved denne pH. Dette ses af Bjerrumdiagrammet nedenunder:

   

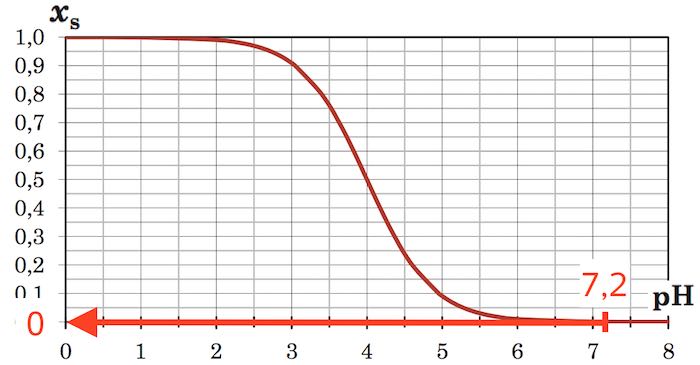
3. Man benytter absorbtionskurven, der gælder for syre-base parret ved pH 7,2. Her aflæses absorptionen til 1,15.

   

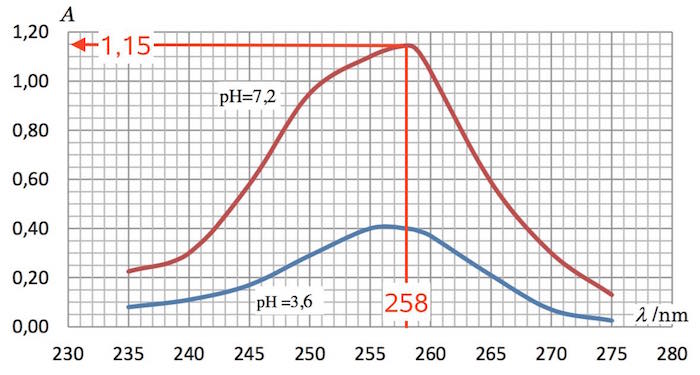
   Man ved fra spørgsmål b), at ved denne pH er [S] ≈ 0 og [B] ≈ C_s = 5,0·10^-5 M.

   Her står S for barbitursyre og B for barbiturat.

   Man har i følge Lambert-Beers lov: A = ε_S,258·[S]·(1 cm) + ε_B,258·[B]·(1 cm), hvor

      A er opløsningens absorbans (ubenævnt),

      ε_S,258 er den molare absorbtionskoefficient for barbitursyre ved bølgelængden 258 nm

      ε_B,258 er den molare absorbtionskoefficient for barbiturat ved bølgelængden 258 nm

   Man får:

   A = ε_S,258·0·(1,00 cm) + ε_B,258·(5,0·10^-5 M)·(1,00 cm) ⇒

   ε_B,258 = (5,0·10^-5 M)·(1,00 cm)/1,15 = 2,30·10⁴ M^-1·cm^-1

   Dvs. den molare absorbtionskoefficient for barbiturat ved bølgelængden 258 nm er

   2,3·10⁴ M^-1·cm^-1

4. Man skal finde x_B = 1 - x_S ved pH = 3,6. Dette kan gøre ved at aflæse x_S af Bjerrumdiagrammet og trække det fra 1.

   

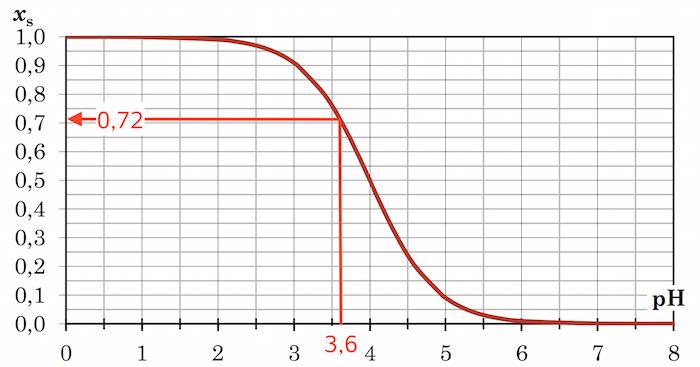
   Heraf fås at x_B = 1 - 0,72 = 0,28 = 28 %

   Da der bedes om en beregning er det nok meningen, at man skal bruge pufferligningen.

   Af pufferligningen får man

   pH = pK_S + log([B]/[S]) ⇒ [B]/[S] = 10^{pH - pK_S} ⇒ [B]/[S] = 10^{3,6 - 4,0} ⇒ [B]/[S] = 0,398107.

   Man skal finde x_B og har at x_B = [B]/([B] + [S]). Divideres i tæller og nævner med [S] får man:

   x_B = ([B]/[S])/([B]/[S] + 1) = (0,398107)/(0,398107 + 1) = 0,284747.

   Dette vil sige at andelen af barbiturat i opløsnngen er 0,2847 = 28,5 %

   For at finde den molare absorptionskoefficient for barbitursyre bruger man som før Lambert-Beers lov og får

   A = ε_S,258·[S]·(1 cm) + ε_B,258·[B]·(1 cm), hvor

      ε_S,258 er den molare absorptionskoefficient for barbitursyre.

   Man har [S] = x_S·C_S ⇒ [S] = (1 - x_B)·C_S ⇒ [S] = (1 - 0,285)·(5,0·10^-5 M) ⇒

   [S] = (0,715)·(5,0·10^-5 M) ⇒ [S] = 3,575·10^-5 M.

   Man har på samme måde [B] = x_B·C_S ⇒ [B] = 0,285·5,0·10^-5 M ⇒ [B] = 1,425·10^-5 M.

   Desuden har man fra tidligere, at ε_B,258 = 2,3·10⁴ M^-1·cm^-1.

   Man aflæser A ved pH 3,6 til 0,4:

   

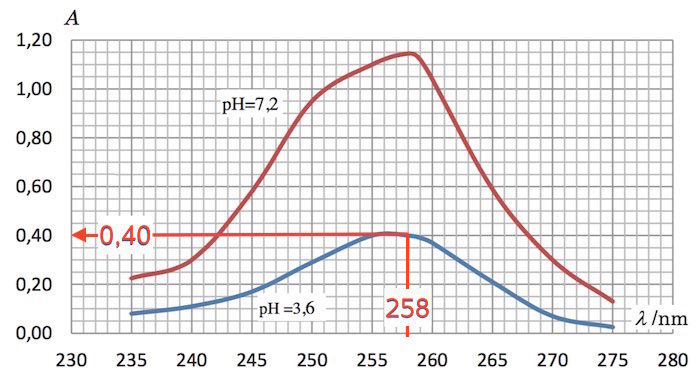
   Dette giver: 0,4 = ε_S,258·(3,575·10^-5 M)·(1 cm) + (23000 M)·(1,425·10^-5 M)·(1 cm) ⇒

   ε_S,258 = (0,4 - (2,3·10⁴ M^-1·cm^-1)·(1,425·10^-5 M)·(1 cm))/((3,575·10^-5 M)·(1 cm)) =

   2020,98 M^-1·cm^-1

   Dvs. den molare absorptionskoefficient for barbitursyre ved bølgelængden 258 nm er

   2,0·10³ M^-1·cm^-1