Svar på opgave 1: Acrylsyre

1. Ved omslag gælder, at n_S = n_B, hvor

      n_S er stofmængden af syre fra start og

      n_B er stofmængden af tilsat base.

   Desuden gælder, at stofmængdekoncentrationen C_S = n_S/V_S, hvor

      V_S er rumfanget af syreopløsning fra start.

   Tilsvarende gælder for stofmængdekoncentrationen af tilsat base: C_B = n_B/V_B ⇒ n_B = C_B·V_B.

   Formlerne sættes sammen, og man får stofmængdekoncentrationen C_S = C_B·V_B/V_S =

   (16 mL)·(0,2 M)/(5 mL) = 0,64 M

2. Ved ækvivalenspunktet indeholder opløsningen vand og propensyres korrespondrende base propenoat. Dette gør at opløsningen er basisk som det ses af pH-værdien 8,72, der er større end 7.

Svar på opgave 2: Et syntetisk duftstof

1. Der er tale om en redoxproces, idet det C-atom, der er bundet til O skifter oxidationstrin fra +2 til +1. Dette er vist på tegningen:

   

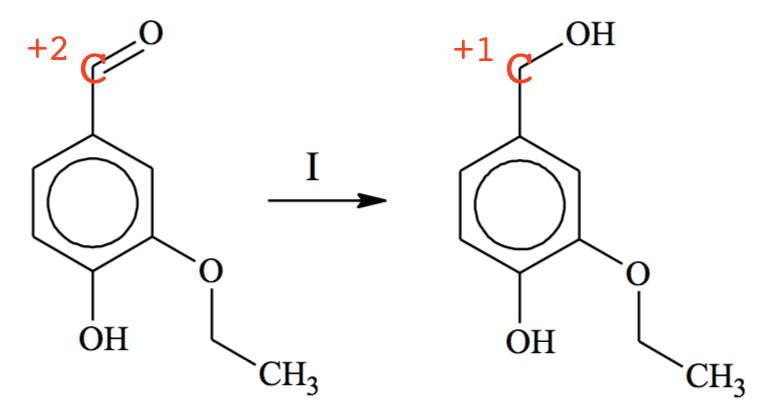
2. Udbyttet er (100 %)·(m_B,m)/(m_B,t), hvor

      m_B,m er den målte masse af B

      m_B,t er den teoretiske masse af B eller massen af B ved fuld omdannelse af A.

   Ved fuld reaktion gælder n_A = n_B, hvor

      n_A er antal mol A fra start

      n_B er antal mol B ved fuld omdannelse af A.

   Dette gælder fordi A og B optræder i forholdet 1:1 i reaktionsligningen.

   Der gælder desuden at m_B,t = n_B,t·M_B = n_A·M_B. Dette giver sammen med det øvrige:

   Udbytte = (100 %)·(m_B,m)/(n_A·M_B) = (100 %)·(1,246 g)/[(9,754·10^-3 mol)·(168,19 g/mol)] = 76 %

3. Når der sker en kondensation ved reaktion med en syre, så er det en esterdannelse, hvor alkoholgruppen reagerer med syren. (Bemærk at -OH, der sidder direkte på benzenringen, ikke kan danne en ester. Denne gruppe er en phenol og ikke en alkohol).

   Man aflæser integralet på NMR diagrammet til 14. Dvs. at antallet af H i molekylet er n·14, hvor n = 1,2...

   Det nemmeste er at antage, at n = 1, hvilket giver det molekyle, der er indtegnet i diagrammet nedenunder. Nedenunder er vist at dette stof passer på NMR-spektret.

   

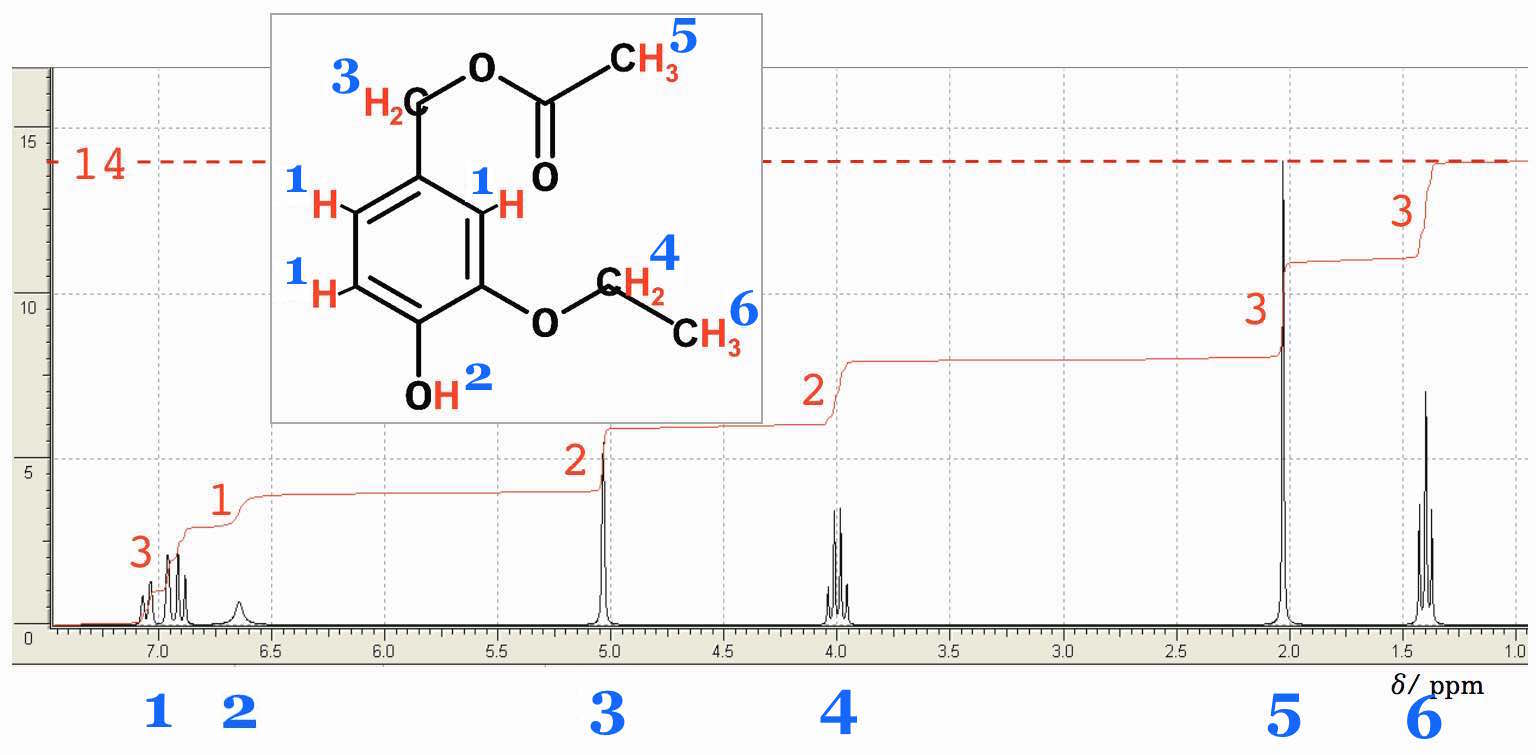
   1) en femdelt top med et kemisk skift på 7 og et integrale på 3 (= 3H). Det passer med de 3 aromatiske H'er, der ikke har helt ens omgivelser, og den femdelte top er derfor ikke en pentet, men to dupletter (de to H'er på venstre side af benzenringen) og en singlet (H'et på højre side). Det høje kemiske skift skyldes deshielding fra benzenringen. I følge tabel ligger det kemiske skift for C₆H₆ på 7,3.

   2) en singlet med et kemisk skift på 6,5 og et integrale på 1 (= 1H). Det passer med H'et på -OH. Dette H giver en singlet, da det ikke sidder på et C-atom og derfor ikke kobler med andre H-atomer. Det høje kemiske skift skyldes deshielding fra O. I følge tabel ligger det kemiske skift for Ar-OH på 4,5-10 afhængigt af temperatur, pH og opløsningsmiddel.

   3) En singlet med 2 H'er og et kemisk skift på 5. Dette passer med de 2 H'er, der sidder på C-atomet der forbinder benzenringen med O'et i esterbindingen. Disse H'er kobler ikke med andre H'er, da det C-atom, som de sidder på ikke er bundet til andre C-atomer, der er bundet til H. Det høje skift skyldes dels benzenringen, dels igen O. Ingen af disse er dog bundet direkte til H og derfor deshieldes H'erne lige så meget som i tilfælde 1 og 2). I følge tabel ligger det kemiske skift for -C-CH-O-CO-R på 4,8.

   4) En kvartet med integralet 2 og et kemisk skift på 4,0. Dette passer med de to H, der sidder på det næstyderste C-atom på sidegrenen, der starter med O. Disse H'er deshieldes af O'et som C'et er bundet til. Dette giver en middelstor deshielding som i tilfældet med 3). I følge tabel ligger det kemiske skift for -C-CH₂-O-Ar på 4,3.

   5) En singlet med integralet 3 og et kemisk skift på 2,0. Dette passer med de tre H, der sidder yderst på esterdelen. Disse H'er deshieldes af O'et, som nabo C-atomet er bundet til. Dette en giver en lille deshielding, da O'et hverken er bundet direkte til H eller til det C, som H'erne sidder på. I følge tabel ligger det kemiske skift for CH₃-CO-O-R på 2,0.

   6) En triplet med integralet 3 og et kemisk skift på 1,4. Dette passer med de tre H, der sidder yderst på æterdelen. Disse H'er deshieldes ligesom i tilfælde 5) af et O, som nabo C-atomet er bundet til. Dette en giver en lille deshielding som før. I følge tabel ligger det kemiske skift for CH₃-C-O på 1,3.

Svar på opgave 3: Ny medicin til behandling af ADHD

1. Molekyleformlen for atomoxetin er C₁₇H₂₁NO. (Først C, H og dernæst andre grundstoffer i alfabetisk orden).

2. Syrebrøken x = n_S/(n_S + n_B) = 1/(1 + (n_B/n_S)) ⇒ n_B/n_S = 1/x - 1.

   Her er n_S antal mol syre og n_B antal mol af dens korresponderende base.

   Pufferligningen giver: pH = pK_S + log(n_B/n_S) ⇒

   pH = pK_S + log(1/x - 1) ⇒

   pH = (14 - pK_B) + log(1/x - 1) ⇒

   7,4 = (14 - 4,77) + log(1/x - 1) ⇒

   x = 0,985

   Dvs. syrebrøken er 98,5 %

3. Man bruger udelukkelsesprincippet for at finde ud af hvilke bindingstyper, som adskiller de forskellige stoffer. Stofferne er vist nedenunder.

   

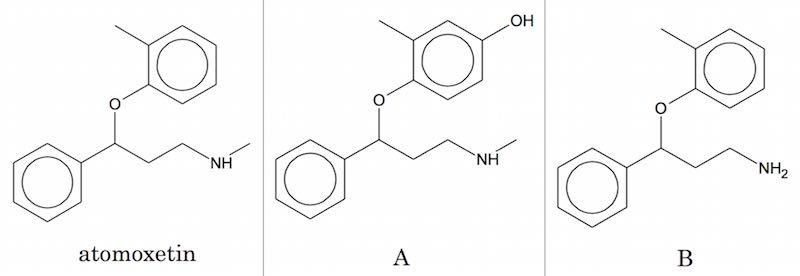
   Atomoxetin har hverken O-H eller sekundær amin.

   A har O-H og sekundær amin.

   B har ikke -O-H, men primær amin.

   Alle stoffer har C-H, C-N, N-H og C-O.

   I følge tabel giver O-H og N-H bindinger begge en top omkring 3000-3500 cm^-1. Det må formodes, at A's top er større end de andres på grund af O-H. B har en primær amin, der giver en middelstor bred top omkring 1500-1600 cm^-1.

4. Kurven nedenunder viser i princippet koncentrationen af stoffet som funktion af tiden. De første 2 timer opløses stoffet og blandes med blodet, samtidig nedbrydes noget af det.

   

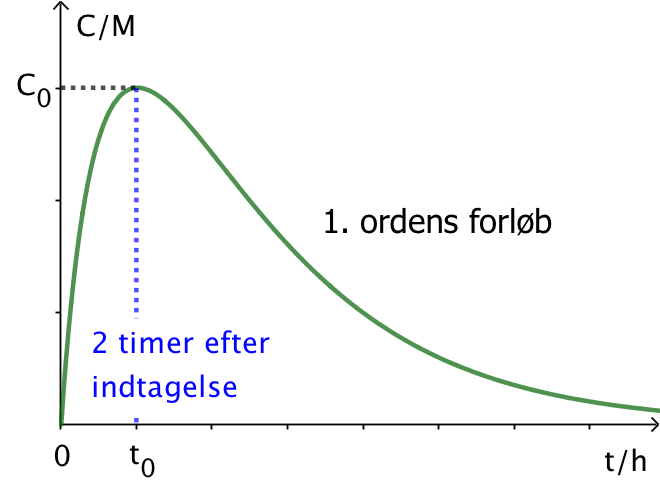
   Efter 2 timer er alt stoffet opløst og 85 % af det er tilbage. Tidspunktet kaldes t₀ (starten for førsteordens reaktionen)

   Der gælder: C(t) = C₀·exp(-t·ln(2)/T_1/2), hvor

      C(t) er koncetrationen af stof som funktions af tiden (t) efter, at førsteordens reaktionen
      begynder,

      C₀ er koncentrationen af stof til tiden t₀ og

      T_1/2 er halveringstiden.

   Der gælder i øvrigt: C₀ = (85 %)·(m/M)/V, hvor

      m er massen af atomoxetin ved indtagelse,

      M er molmassen af atomoxetin og

      V er blodvolumenet.

   Dette giver: C₀ = (85 %)·(60mg/255 g/mol)/(4,5 L) = 4,44·10^-5 M

   Man får: C(1 døgn) = (4,44·10^-5 M)·exp(-(1 døgn)·ln(2)/(5,2 døgn)) = 5,1·10^-5 M.

   Dvs. stofmængdekoncentrationen af atomoxetin i blodet efter et døgn er 5,1·10^-5 M

5. Ved lave pH-værdier er atomoxetin på ionform, da det er en base (den indeholder en sekundær amin) som optager H⁺.

   Ved høje pH-værdier er atomoxetin ikke på ionform og da det indeholder mange hydrofobe grupper, vil man forvente en lav vandopløselighed ved disse pH-værdier.

   Man skal derfor forvente at andelen af atomoxetin er høj i vandfasen og omvendt lille i octanol-fasen ved lave pH-værdier. Det omvendte vil gælde ved høje pH-værdier.

   Da K_F er forholdet mellem de to andele, vil der gælde, at jo lavere pH, jo lavere K_F og omvendt jo højere pH, jo større K_F. Dette passer med tabellens tal.

Svar på opgave 4: Chlorofyl i spinat

1. Der er tre slags funktionelle grupper, der indeholder O som vist på billedet nedenunder:

   

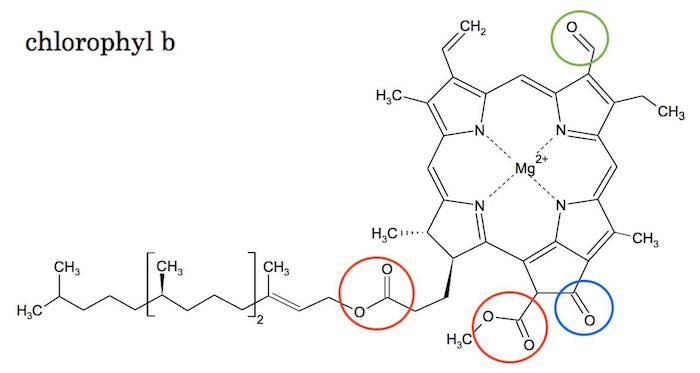
   1 aldehyd (grøn ring)

   1 keton (blå ring)

   2 estere (røde ringe)

   (Aldehyder og ketoner kaldes samlet carbonylgrupper.)

2. Man laver lineær regression på tabellens tal som vist (husk at enheden for koncentration er mikromolær).

   

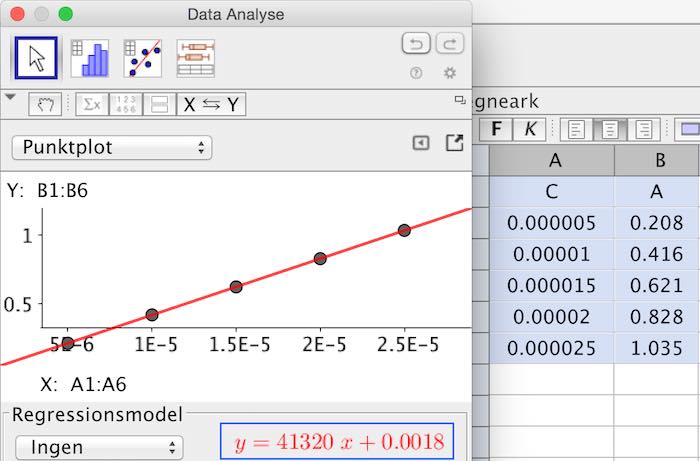
   Regressionsformlen er som vist med den blå ramme: y = 41320·x + 0,0018.

   Den molare absorptionskoefficient er hældningen til kurven, hvilket følger af Lambert-Beers lov: A = ε·C·L, hvor

      A er absorbansen (dimensionsløs)

      ε er den molare absorbtionskoefficient

      C er koncentrationen og

      L er den distance, som lyset tilbagelægger gennem væsken (= 1 cm).

   I regressionsformlen svarer y til A og C svarer til x, hvilket vil sige, at ε svarer til hældningen 41320.

   Det konstante led i regressionsformlen burde være 0, men afvigelsen kan forklares med måleusikkerhed.

   Dette viser, at den molare absorptionskoefficient er 4,13·10⁴ M^-1cm^-1.

3. Man har to ligninger med to ubekendte med hensyn til koncentrationen af chlorophyl_a og chlorophyl_b.

   Man bruger Lambert-Beers lov for begge sæt af koncentrationer, absobans og molar absorbtionskoefficienter. Dette giver:

   A₆₄₅ = C_a·ε_a,645 + C_b·ε_b,645

   A₆₆₃ = C_a·ε_a,663 + C_b·ε_b,663

   Her er

      A₆₄₅ den samlede absorbans af chlorophyl_a og chlorophyl_b ved 645 nm,

      A₆₆₃ den samlede absorbans af chlorophyl_a og chlorophyl_b ved 663 nm,

      C_a koncentrationen af chlorophyl_a,

      C_b koncentrationen af chlorophyl_b,

      ε_a,645 den molare absorptionskoefficient af chlorophyl_a ved bølgelængden 645 nm,

      ε_a,663 den molare absorptionskoefficient af chlorophyl_a ved bølgelængden 663 nm,

      ε_b,645 den molare absorptionskoefficient af chlorophyl_b ved bølgelængden 645 nm og

      ε_b,663 den molare absorptionskoefficient af chlorophyl_b ved bølgelængden 663 nm.

   De sammenhørende ligninger løses i Ti-Nspire:

   solve(0.469=ca*1.5*10⁴+cb*4.13*10⁴ and 0.998=ca*7.33*10⁴+cb*8.41*10³,ca,cb) ▸ ca=0.000012848 and cb=0.00000669

   Dvs. C_a = 0,000012848 M = 1,29.10^-5 M og C_b = 0,00000669 M = 6,69·10^-6 M.

   Dette skal regnes om til mg chlorophyl pr. 100 g spinat.

   Man går baglæns for at finde massen af chlorophyl_a og chlorophyl_b i de 100 mL spinatekstrakt. Denne er lig med stofmængden af chlorophyl_a og chlorophyl_b i 5 g spinat.

   Det giver:

   c_a = (m_a/m_spinat) = (n_a·M_a/m_spinat) = (C_a·V_ekstrakt·M_a/m_spinat), hvor

      c_a er koncentrationen af chlorophyl_a målt i g chlorophyl_a pr. g spinat,

      m_a er massen af chlorophyl_a i prøven med spinat,

      M_a er molmassen af chlorophyl_a = 893,49 g/mol,

      V_ekstrakt = 100 mL = 0,1 L og

      m_spinat er massen af prøven af spinat = 2 g

   Tallene indsættes:

   c_a = (1,29.10^-5 mol chlorophyl_a/L ekstrakt)·(0,1 L ekstrakt)·(893,49 g chlorophyl_a/mol chlorophyl_a)/(2 g spinat) =

   0,0005763 (g chlorophyl_a)/(g spinat) =

   0,5763 (10³·10^-3 g chlorophyl_a)/(10²·10^-2 g spinat) =

   0,0005763·10³·10² (10^-3 g chlorophyl_a)/(10² g spinat) =

   0,0005763·10⁵ (mg chlorophyl_a)/(100 g spinat) = 57,6 (mg chlorophyl_a)/(100 g spinat)

   Tilsvarende får man for chlorophyl_b (idet molmassen af chlorophyl_b er 907,47 g/mol):

   c_b = (6,69·10^-6 M)·(0,1 L)·(907,47 g/mol)/(2 g) =

   0,000304 (g chlorophyl_b)/(g spinat) = 30,4 (mg chlorophyl_b)/(100 g spinat)

Svar på opgave 5: Opsamling af carbondioxid

1. 2·n mol LiOH reagerer med 1·n mol CO₂ i følge reaktionsligningen. Her er n et reelt tal.

   Molmassen af LiOH er 23, 95 g/mol. Der gælder:

   m_CO2 = M_CO2·(1/2)·n_LiOH = M_CO2·(1/2)·(m_LiOH/M_LiOH) ⇒

   m_CO2 = (44,01 g/mol)·(1/2)·(3900 g/23,95 g/mol) = 3,58 kg

   Dvs. skrubberen kan maksimalt absorbere 3,58 kg CO₂

2. ΔH^⊖ = (Δ_fH^⊖_LiCO3 + Δ_fH^⊖_H2O) - (2·Δ_fH^⊖_LiOH + Δ_fH^⊖_CO2) =

   [(-1215,6 - 285,83) - (-487,5 - 393,51)] kJ/mol = -132,92 kJ/mol

   Her er Δ_fH^⊖_stof den molære standard dannelsesentalpi af stoffet i parentes.

   Da reaktionen er eksoterm mod højre, så betyder det, at der dannes varme ved den reaktion der foregår i denne retning.

3. Massen af CO₂, der udskilles af en astronaut på 1 døgn, beregnes ved hjælp af idealgasloven:

   m_CO2 = V_CO2·P_CO2·M_CO2/(R·T), hvor

      m_CO2 er massen af CO₂ i g,

      V_CO2 er rumfanget af CO₂ der udskilles pr. døgn = 500 L,

      P_CO2 er partialtrykket af CO₂ = 1,00 bar,

      M_CO2 er molmassen af CO₂ = 44,01 g·mol^-1,

      R er idealgaskonstanten = 0,08314 bar·L·mol^-1·K^-1 og

      T er temperaturen af gassen = 273,15 + 20 K = 293,15 K.

   Man får: m_CO2 = (500 L)·(1,00 bar)·(44,01 g·mol^-1)/((0,08314 bar·L·mol^-1·K^-1)·(293,15 K)) = 902,86 g pr. person pr. døgn.

   For 3 personer på 10 døgn bliver den samlede masse af udskilt CO₂ = 3·10·902,86 g = 27.086 g.

   Hver enkelt skrubber absorberer (75 %)·(3900 g) = 2.925 g.

   Antallet af skrubbere bliver (27,086 g)/(2,925 g) = 9,4, som rundes op til 10 skrubbere for at få et antal, som er tilstrækkeligt.

4. Ligevægstkonstanten K = exp(ΔG^⊖(20 °C)/(R·T)), hvor

   ΔG^⊖(20 °C) er reaktionens Gibbs frie energi ved 20 °C,

   R er gaskonstanten = 8,314 J·mol^-1·K^-1

   T er gassens absolutte temperatur = 293,15 K.

   ΔG^⊖(20 °C) = ΔH^⊖ - T·ΔS^⊖, hvor

   ΔS^⊖ er ændringen i entropi ved reaktionen (mod højre).

   ΔS^⊖ findes som før af dannelses entropierne for de indgående stoffer :

   ΔS^⊖ = (Δ_fS^⊖_LiCO3 + Δ_fS^⊖_H2O) - (2·Δ_fS^⊖_LiOH + Δ_fS^⊖_CO2) =

   [90,37 + 69,95 - (2·42,8 + 213,785 )] J·mol^-1·K^-1 = -139,07 J·mol^-1·K^-1

   Man får nu: ΔG^⊖(20 °C) = -132,92·10³ J·mol^-1 - (293,15 K)·(-139,07 J·mol^-1·K^-1) = 92174 J·mol^-1

   Det giver K = exp(92174 J·mol^-1/((8,314 J·mol^-1·K^-1)·(293,15 K))) = 2,62·10¹⁶ bar^-1.

   Dvs. ligevægtkonstanten for reaktionen ved 20 °C er 2,62·10¹⁶ bar^-1

   Der gælder at K = 1/p_CO2, hvor p_CO2 er partialtrykket af CO₂ ved ligevægt.

   Det ses, at p_CO2 = (1/2,62·10¹⁶) bar = 3,8·10^-17 bar, der er langt under det tryk, som CO₂ ellers ville have haft, og skrubberne er derfor i stand til at fjerne meget CO₂ fra luften.

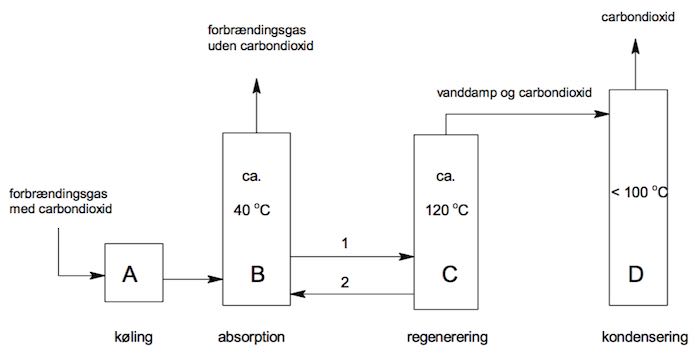
5. I tårn-B absorberes CO₂ af 2-aminoethanol og vand. Forbrændingsgasser ud over CO₂ ledes ud for oven.

   Gennem rør-1 føres blandingen af vand, 2-aminoethanol og opløst CO₂ til tårn-C. Her gør temperaturen på 120 °C (der er over vands og CO₂ kogepunkt, men under 2-aminoethanols) at vand og CO₂ ledes væk som gasser for oven, mens 2-aminoethanol ledes tilbage til tårn-B gennem rør-2.

   I tårn-D fortættes vanddamp til vand (temperaturen er under 100 °C, der er vands kogepunkt), mens CO₂ ledes bort som gas på ren form foroven.