Svar på opgave 1: Jasminolie
-
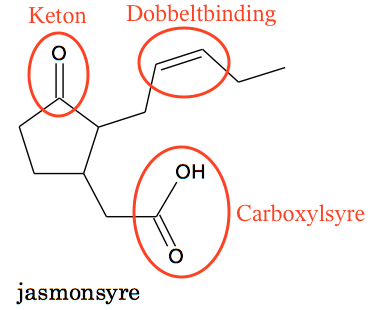
Nedenfor er de funktionelle grupper tegnet ind.
-
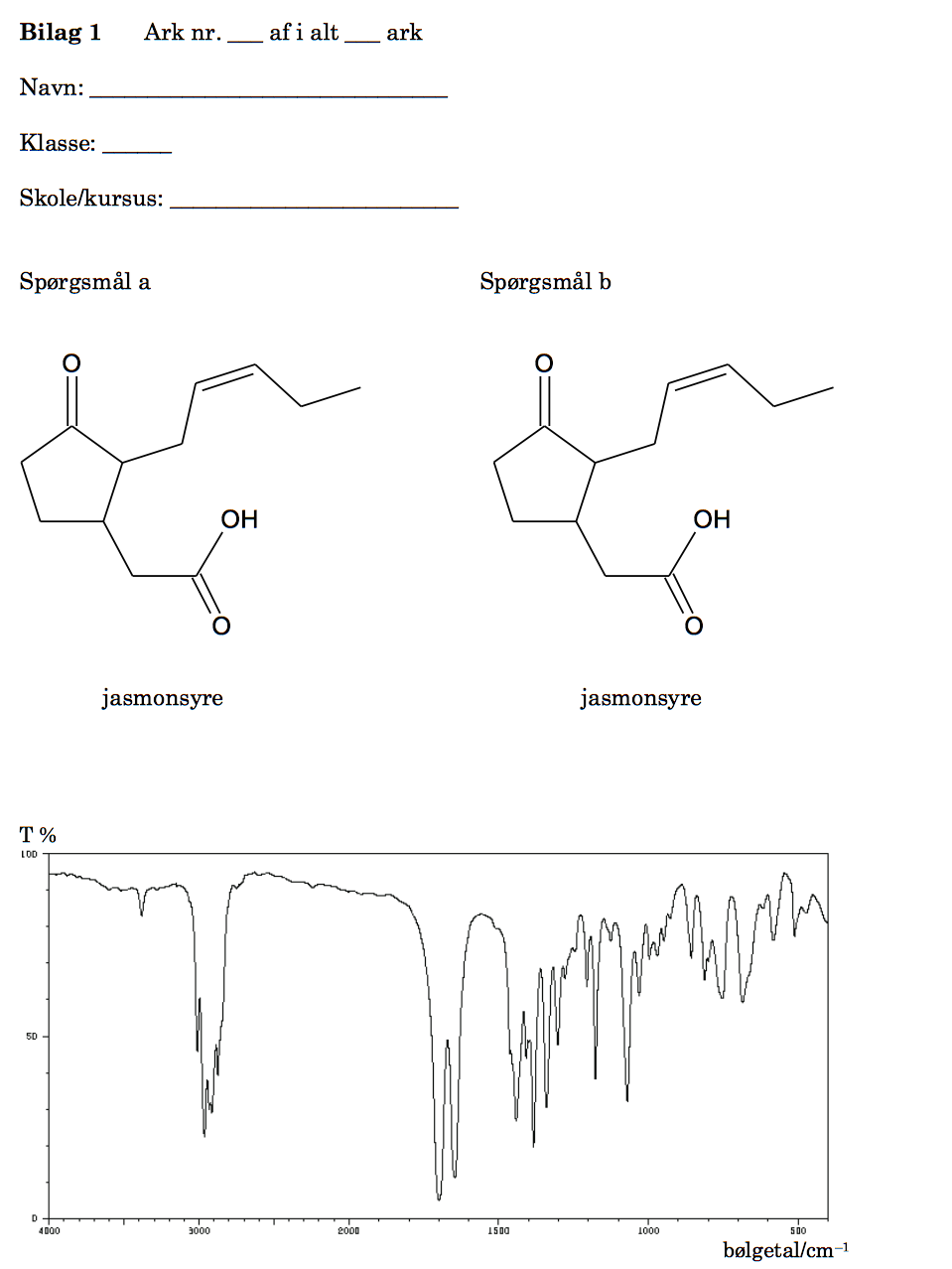
De to typer af stereoisomeri er geometrisk isomeri eller cis-/trans-isomeri og enantiomeri også kaldet optisk isomeri eller spejlbilledisomeri. Geometrisk isomeri forekommer i forbindelse med C=C dobbeltbindinger.
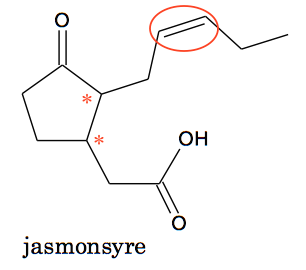
Spejlbilledisomeri kan forekomme i forbindelse med asymmetriske C-atomer. Nedenunder er C=C dobbeltbindingen indrammet med en ring, og de asymmetriske C-atomer er markeret med en stjerne (*).
-
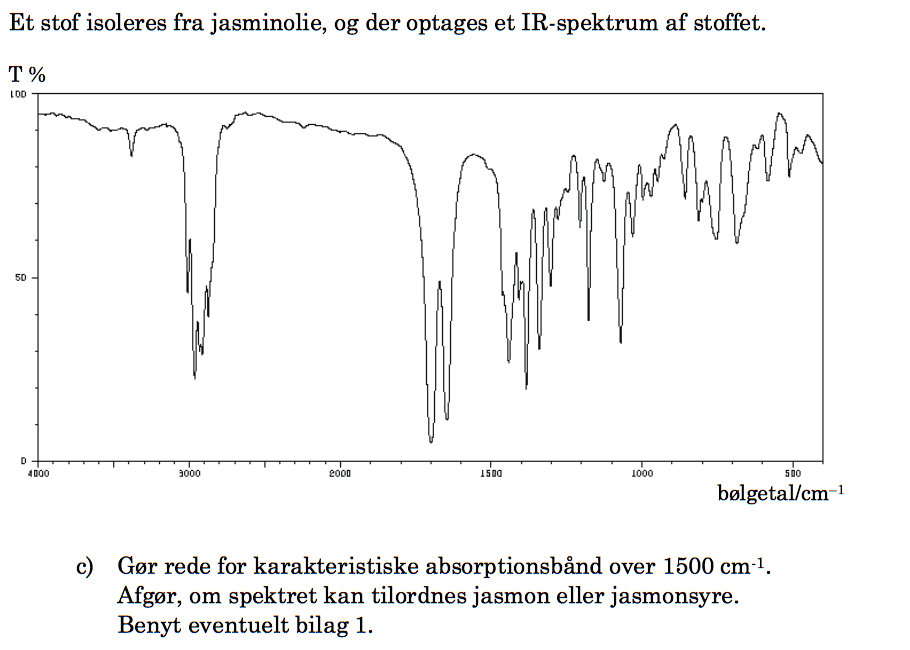
Der er toppe fra strækning i forbindelse med C-H fra alkan, C-H fra alken, C=O fra carbonyl og C=C fra alken. Dette er vist på billedet nedenunder.
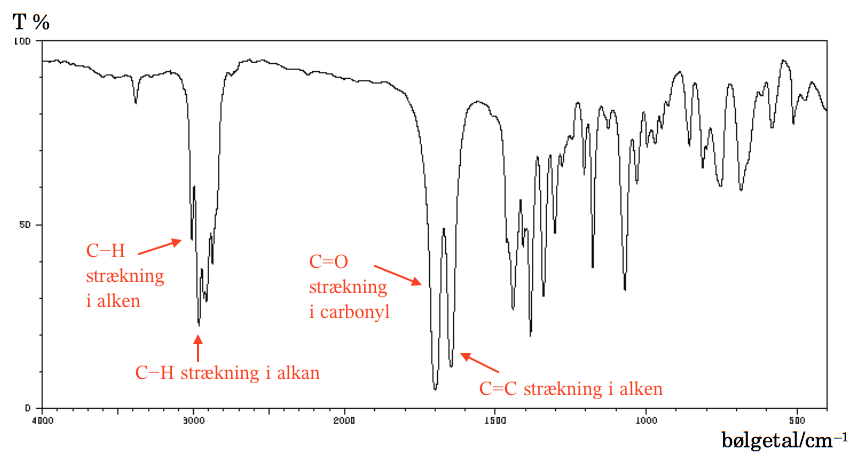
På IR-spektret mangler en bred top omkring 3000 cm-1 fra O-H strækning i carboxylsyre. Man konkluderer derfor, at stoffet er Jasmon
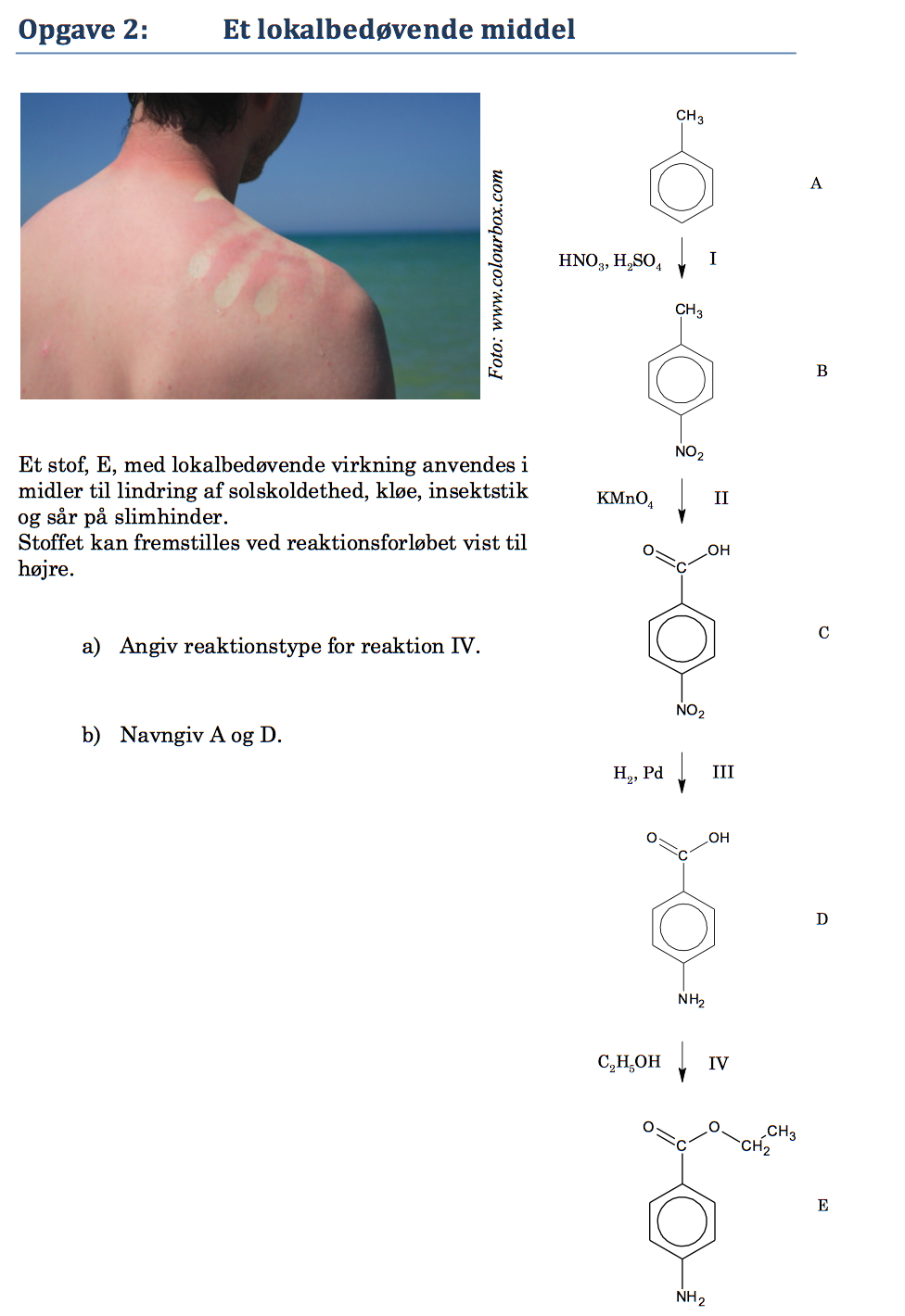
Svar på opgave 2: Et lokalbedøvende middel
-
Reaktion IV er en esterdannelse eller estersyntese.
Den er samtidig et eksempel på en kondensation, dvs. fraspaltning af H2O, selvom det ikke er vist.
-
A er toluen og D er 4-aminobenzosyre (også kaldet para-aminobenzosyre eller PABA).
-
En førsteordens reaktion med hensyn til stoffet E følger formlen:
[E]t = [E]0·e-k·t
Her er [E]t koncentrationen af E som funktion af tiden, [E]0 er startkoncentrationen af E, k er hastighedskonstanten og t er tiden (her målt i sekunder).
Når 90 % af E er omdannet er der 10 % tilbage. Der gælder ved det tidspunkt:
[E]t = 0,1·[E]0 ⇒ [E]0·e-k·t = 0,1·[E]0 ⇒ e-k·t = 0,1.
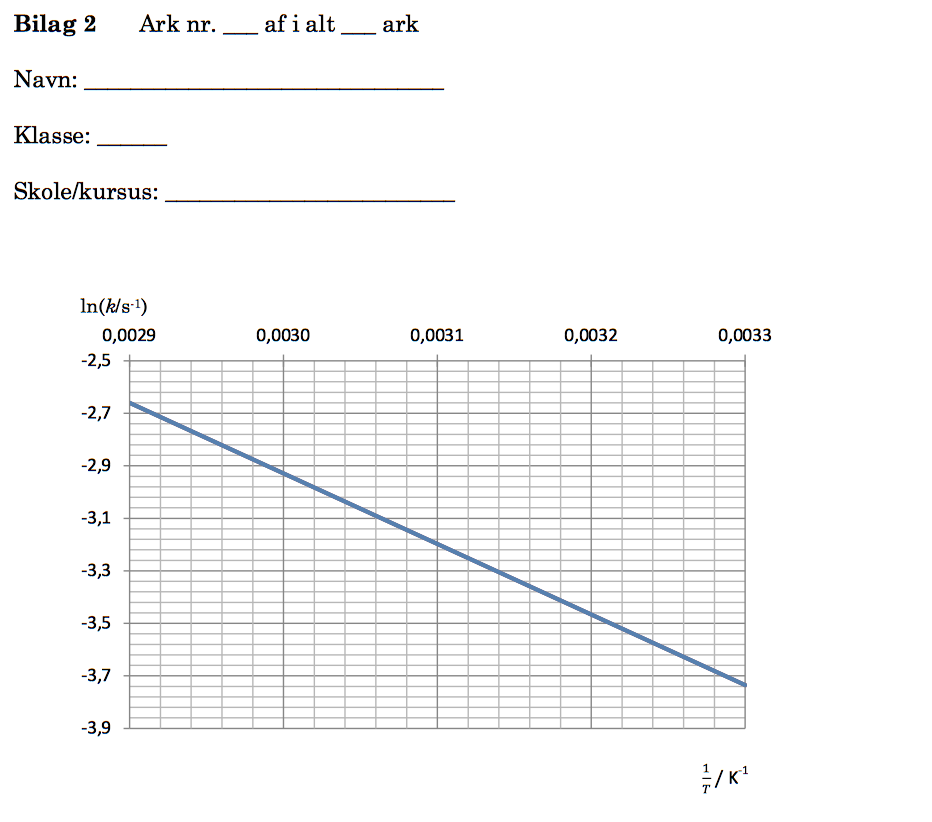
Hastighedskonstanten k kan findes ud fra grafen af ln(k) som funktion af 1/T. Man finder først Kelvintemperaturen: T = 20 + 273 K = 293 K. Det giver: 1/T = 0,0031 K-1. Man aflæser derefter ln(k) på grafen:
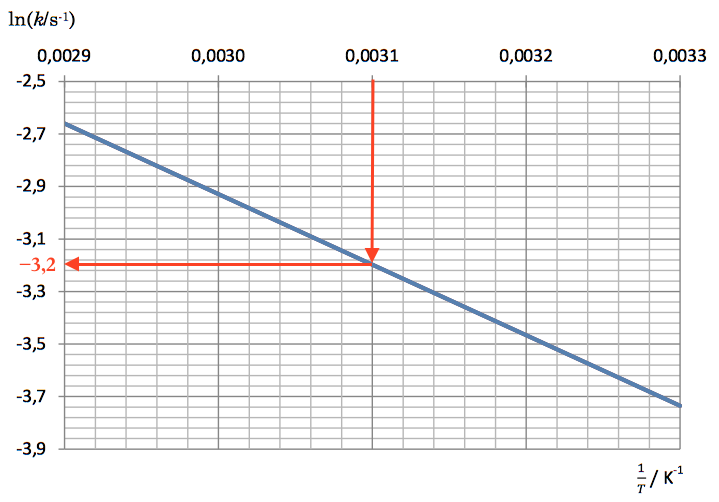
ln(k) = -3,2. Dette giver: k = e-3,2 = 0,0408. Dette indsættes i ovenstående formel:
e-0,0408·t = 0,1 ⇒ t = 56, dvs. der går 56 sekunder før 90 % af stoffet er omdannet.

Svar på opgave 3: Clenbuterol
-
Man skal bestemme den molære koncentration eller koncentrationen i mol pr. liter. Man har:
C = n/V = (m/M)/V = (m/V)/M, hvor
C er den molære koncentration af clenbuterol,
n er stofmængden af clenbuterol,
V er rumfanget af opløsningen,
m er massen af clenbuterol og
M er molmassen af clenbuterol.
Man ved, at m/V = 5·10-8 g/L. Dette indsættes i formlen:
Den molære koncentration af clenbuterol = C = (m/V)/M = (5·10-8 g/L)/(277,19 g/mol) = 1,8·10-10 M
-
Afbildningen af ln(C) som funktion af tiden er en ret linje. Dermed gælder at
C = C0·e-k·t
hvilket viser at reaktionen er første orden med hensyn til koncentrationen af clenbuterol. Her er C = koncentrationen af clenbuterol, C0 er startkoncentrationen, k er hastighedskonstanten og t er tiden i timer.
Halveringstiden T er lig med ln(2)/k. Af grafen har man regressionsformlen:
y = -0,034·x + 1,496, der også kan skrives: ln(C) = -0,034·C + 1,496. Her kan k aflæses som -1 gange koefficienten til C, som giver k = 0,034.
Heraf følger: T = ln(2)/0,034 = 20,4. Dvs. halveringstiden for koncentrationen af clenbuterol er 20,4 timer
-
R er en alkylgruppe. Dvs. at den har bruttoformlen: -CnH2n+1. Man starter med at beregne n, der er antal C-atomer i R.
Masseprocenten af C-atomer i et mol af hele molekylet er 52 %. Massen af C-atomer i et mol af molekylet er x·MC, hvor x er antal C-atomer i et molekyle og MC er molmassen af C-atomer, som er lig med 12,0 g/mol. Dette giver:
x·(12,0 g/mol)/(277,19 g/mol) = 52 % ⇒
x = (52 %)/[(12,0 g/mol)/(277,19 g/mol)] = 0,52·(277,19 g/mol)/(12,0 g/mol) = 12.
Dvs. clenbuterol indeholder 12 C-atomer. På strukturformlen kan man tælle 8 C-atomer som vist nedenunder:
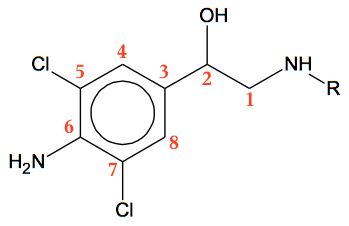
Dvs. R har bruttoformlen: -C4H9.
Det kemiske skift på 1,25 passer med, at R er en alkylgruppe, sådan som man har fået oplyst. Det at alkylgruppens H-atomer danner en singlet, viser at alle H-atomerne sidder på et C-atom som er bundet til et C-atom, der ikke indeholder H. Dvs. at stukturen for R er:
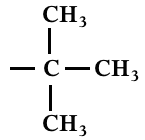
-
Arealtallet for clenbuterol er indrammet på figuren nedenunder.
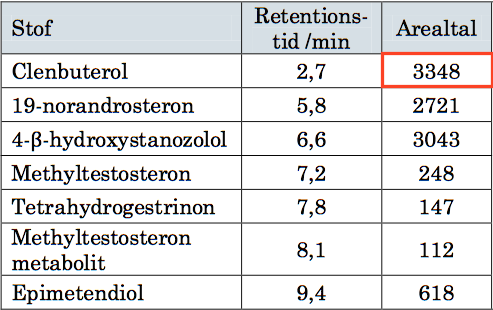
Man tegner en kurve af arealtal som funktion af koncentration for at kunne aflæse koncentationen af clenbuterol. Det er lavet i Ti-Nspire og er vist nedenunder:
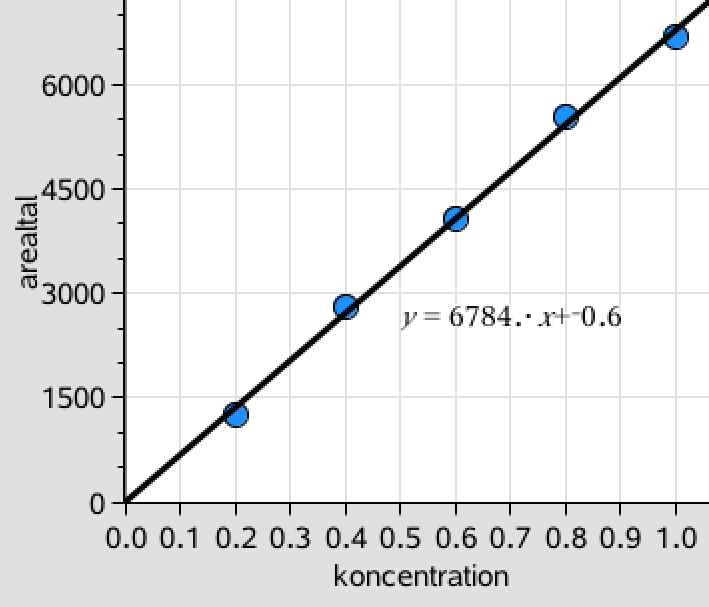
Det ses at punkterne ligger på en ret linje med regressionsligningen arealtal = 6784·C - 0,6. Man indsætter arealtal = 3348 i ligningen og løser den med hensyn til koncentrationen (C):
3348 = 6784·C - 0,6 ⇒ C = 0,494. Dvs. Koncentrationen af clenbuterol = 0,494 μg/L
-
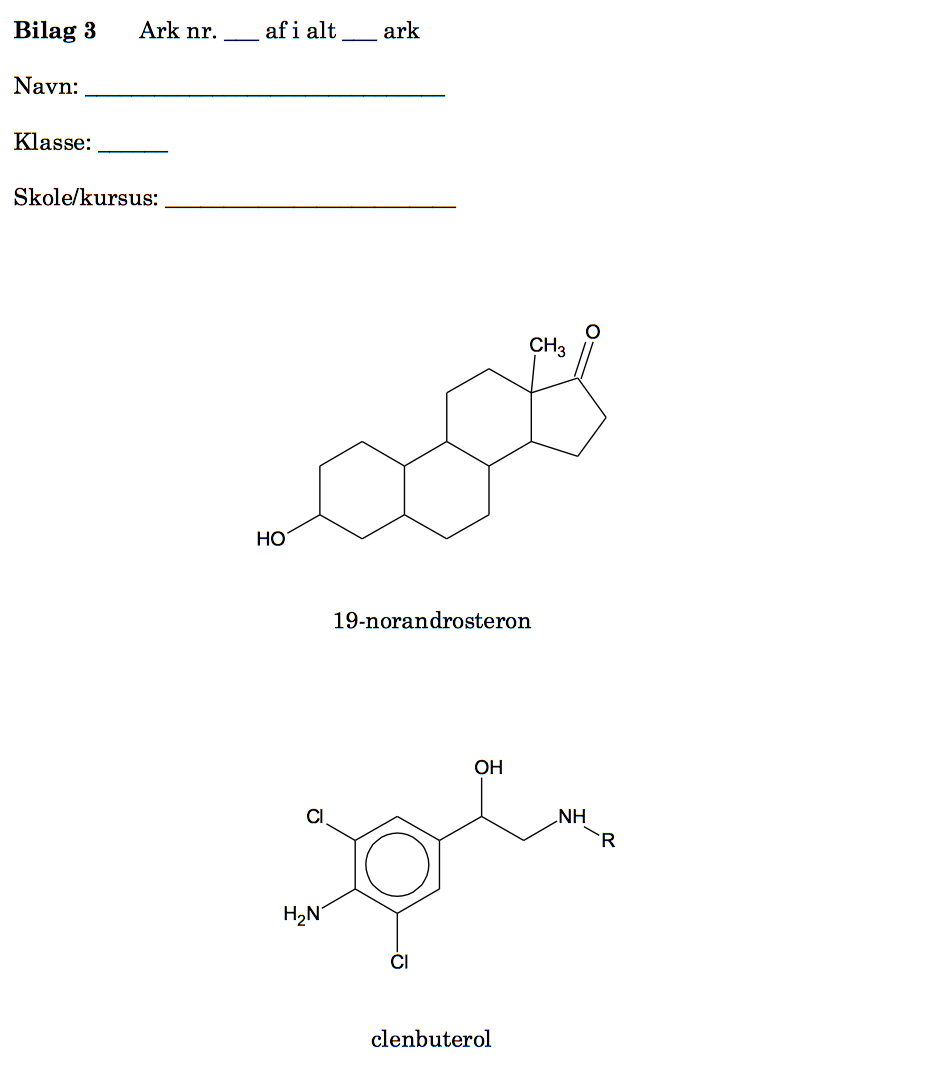
Retentionstiden afhænger af hvor polært stoffet er. Da den stationære fase er upolær, vil der gælde, at jo mere upolært et stof er, jo længere retentionstid.
Ved at betragte de to stoffers strukturformler, hvor de polære grupper er makreret, ser man at 19-norandrosteron har færre polære grupper i forhold til antallet af kulstofatomer i molekylet og dermed er mindst upolært.
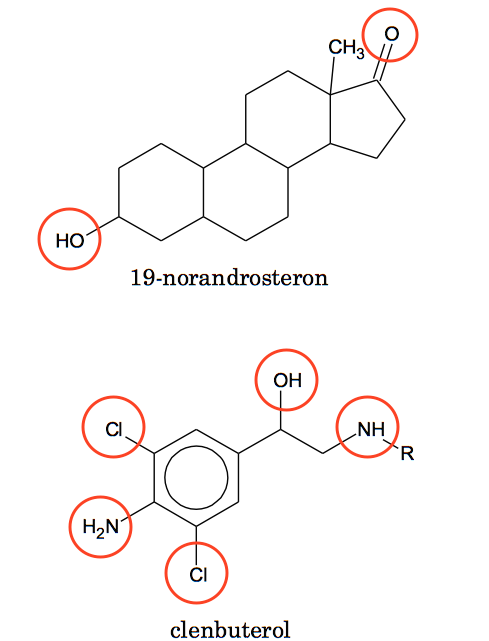
Derfor har clenbuterol kortere retentionstid end 19-norandrosteron. Ved lav pH (høj koncentration af H+) vil clenbuterol optage H+ og blive ionisk, som vist nedenunder.
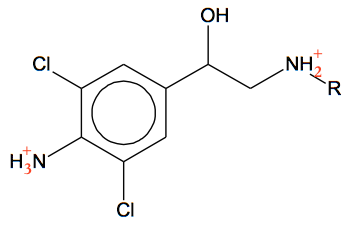
Ved at blive ionisk øges vsndopløseligheden for clenbuterol og dens vil retentionstiden nedsættes yderligere. 19-norandrosteron er hverken syre eller base, og dens retentionstid påvirkes ikke af pH.
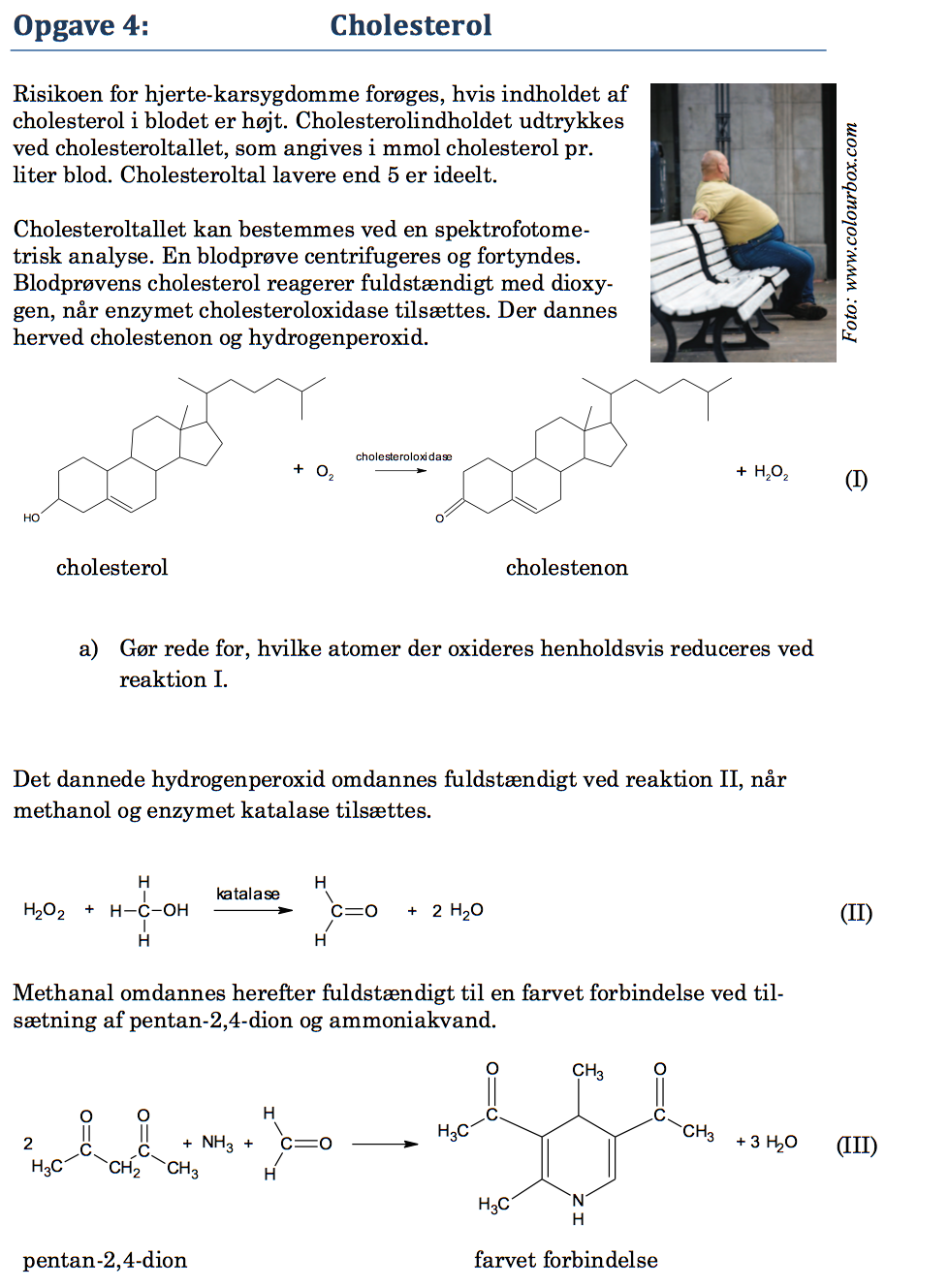
Svar på opgave 4: Cholesterol
-
C-tomet, der er bundet til O oxideres, det går fra oxidationstal +1 til +2. Det frie ilt eller O2, reduceres, idet det går fra oxidationstrin 0 i O2 til oxidationsrtrin -1 i H2O2. Dette er vist nedenunder:
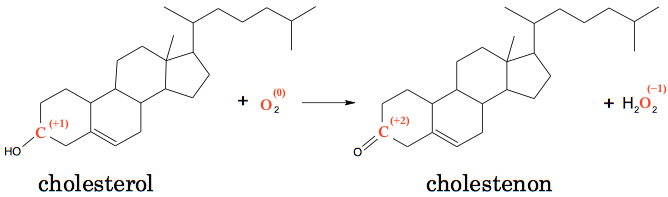
-
Meningen med blindprøven er, at den skal indeholde de samme stoffer som den rigtige prøve på nær det farvede stof. På den måde kan absorbansen af det farvede stof findes ved at trække absorbansen af blindprøven fra absorbansen af prøven med farvet stof.
Koncentrationen af farvet stof kan beregnes ud fra absorbansen, når man kender ekstintionskoefficienten af det farvede stof eller man har en kurve over sammenhængen mellem det farvede stofs koncentration og dets absorbans.


Svar på opgave 5: Binding til et enzym
-
pKb = -log(Kb) = -log(1,15·10-6) = 5,94
pKs = 14 -log(Kb) = 14 - 5,94 = 8,06
-
pH = 14 - pOH =
14 - 0,5·(pKb - log(Cb)) =
14 - 0,5·(5,94 - log(0,1)) =
14 - 0,5·(5,94 + 1) = 10,5
-
Startkoncentrationen af tris er [(0,5 L)/(1 L)]·(0,1 M) = 0,05 M.
Startkoncentrationen af H+ er [(0,021 L)/(1 L)]·(1 M) = 0,021 M.
Ved slutningen af reaktionen har alt H+ reageret. Dvs. slutkoncentrationen af tris er (0,05 - 0,021) M = 0,029 M. Slutkoncentrationen af trisH+ = 0,021 M, da mængden af dannet trisH+ er lig med mængden af H+ fra starten.
Dette er vist på nedenstående figur:
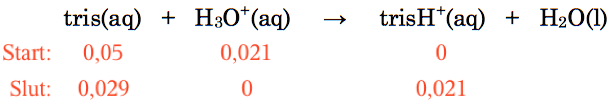
Man finder pH ved hjælp af pufferligningen: pH = pKs + log([B]/[S]) ⇒
pH = 8,06 + log(0,029/0,021) = 8,2
-
Ved ligevægt gælder at ΔGo = -R·T·ln(K)
Man undersøger om ΔGo og -R·T·ln(K) giver det samme:
ΔGo = ΔHo - T·ΔSo = 4070 J/mol - [(20 + 273) K]·73,94 J/mol = -25730 J/mol
-R·T·ln(K) = - 8,314·[(20 + 273) K]·ln(8,3·10-7/[(1,67·10-7)·(1,917·10-5)]) = -24760 J/mol.
Det ses, at lighedstegnet ikke gælder i ovenstående formel og dermed er ligevægt ikke indtrådt
-
Startkoncentrationerne er:
[lysozym]st = [(0,75 mL)/(3 mL)]·10-5 M = 2,5·10-6 M
[eosinY]st = [(0,18 mL)/(3 mL)]·1,65·10-4 M = 9,9·10-6 M
[lysozym-eosinY]st = 0.
Ligevægtskoncentrationerne er:
[lysozym]lv = 2,5·10-6 M - x
[eosinY]lv = 9,9·10-6 M - x
[lysozym-eosinY]lv = x.
x står for stofmængden af omdannet lysozym pr. liter. Dette er samlet nedenfor.

For at bestemme x, har man ligningen:
x/[(2,5·10-6 - x)(9,9·10-6 - x)] = e25734/(8,314·293)
Denne løses i Ti-Nspire og man får x = 6,588·10-7 M eller x = 3,8·10-5 M. Kun den første værdi er gyldig, da x skal være mindre end den mindste startkoncentration af de to reaktanter, der er 2,5·10-6 M.
Andelen af omdannet lysozym er: [lysozym-eosinY]lv/([lysozym-eosinY]lv + [lysozym]lv) = [lysozym-eosinY]lv/[lysozym]st = [(6,59·10-7 M)/(2,5·10-6)]·100 % = 26,3 %.
Dvs. 26,3 % af lysozymmolekylerne er bundet til eosinY ved ligevægt