Svar på opgave 1: Røde bade

1. Der gælder for den koncentrerede KMnO₄-opløsning 1 og den fortyndende opløsning 2, at

   C₁ = n₁/V₁ og C₂ = n₂/V₂, hvor

      C er stofmængdekoncentrationen af KMnO₄ i den givne opløsning,

      n er stofmængden af KMnO₄ og

      V er opløsningens rumfang.

   Man skal finde V₁ rumfanget af den koncentrerede opløsning som tilsættes. Det benyttes, at n₁ = n₂, dvs. at stofmængden af KMnO₄ ikke ændres ved fortynding.

   Dette giver: C₁ = n₁/V₁ og C₂ = n₁/V₂ ⇒ n₁ = C₁·V₁ og n₁ = C₂·V₂ ⇒ C₁·V₁ = C₂·V₂ ⇒

   V₁ = V₂·C₂/C₁ = (2,00·10² L)·(2,0·10^-4 M)/(1,94·10^-1 M) = 0,103 L

   Dvs, der skal bruges 0,103 L af 0,194 M KMnO₄-opløsning.

2. Det er en redoxreaktion, fordi Mn falder i oxidationstrin fra +4 til +2, mens hver af de to C-atomer stiger fra +3 til +4.

3. Der gælder for ligevægtskonstanten (K): K = exp(-ΔG^⊖/(R·T)), hvor

      ΔG^⊖ er den molære standard Gibbs frie energi for reaktionen,

      R er gaskonstanten og

      T er Kelvintemperaturen eller den absolutte temperatur = (25 + 273,15) K = 298,15 K.

   ΔG^⊖ beregnes ud fra dannelses Gibbs frie energierne ved 25 °C for de indgående stoffer i reaktionen. Hver Gibbs energi skal ganges med den koefficient det tilhørende stof har i reaktionsligningen, hvorpå summen for reaktanterne trækkes fra summen for produkterne.

   Disse energier er:

      ΔG^⊖_MnO2(s) = -465,1 kJ/mol

      ΔG^⊖_(COOH)2(aq) = -674,04 kJ/mol

      ΔG^⊖_H⁺(aq) = 0

      ΔG^⊖_CO2(g) = -394,4 kJ/mol

      ΔG^⊖_Mn²⁺(aq) = -228,1 kJ/mol

      ΔG^⊖_H2O(l) = -237,13 kJ/mol

   Dette giver: ΔG^⊖ = (2·(−394,4) + (−228,1) + 2·(−237,13) - (−465,1 + (−674,04) + 0))·10³ J/mol = −352.020 J/mol.

   Heraf følger: K = exp(-(-352.020 J/mol)/((8,314 J·mol^-1·K^-1)·(298,15 K))) = exp(142,08) = 5,08·10⁶¹

   Dvs. ligevægtskonstanten for reaktionen er = 5,08·10⁶¹

   Dimensionen af K. Der er tale om en vanding opløsning i en åben beholder, så man medtager kun koncentrationen af opløste stoffer. I så fald bliver ligevægstudtrykket er: K = [Mn²⁺]/([(COOH)₂][H⁺]²), der har dimensionen M^-2.

   Hvis der er tale om en lukket beholder skal man medregne koncentrationen af opløst CO₂, eftersom den ikke kan betragtes som en konstant. I såfald bliver K dimensionsløs.

Svar på opgave 2: Duften af champion

1. Der er to former for stereoisomeri: spejlbilledisomeri (og diastereomeri) samt E/Z-isomeri (herunder cis/trans-isomeri).

   Her kunne der være tale om cis/trans-isomeri, fordi der er en dobbeltbinding, men det ene C-atom i bindingen har to ens substituenter, så det er ikke tilfældet.

   En anden mulighed er spejlbilledisomeri som følge af et asymmetrisk kulstofatom. Dette ses at være tilstede ved forgreningen og dermed findes molekylet i to spejlbilledisomere former.

   De to spejlbilledisomere former af molekylet er vist på billedet nedenunder, hvor det asymmetriske kulstofatom er markeret med rød stjerne. De to H'er på samme C-atom, der udelukker cis/trans-isomeri er også markeret. Som vist med pile forbliver molekylet ens selvom H'erne bytter plads.

   

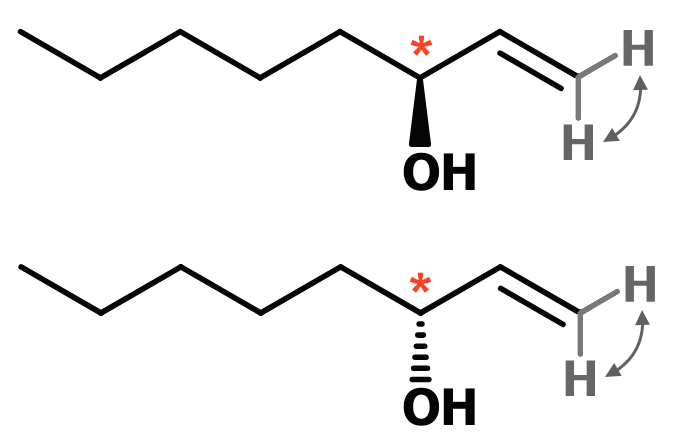
2. Stoffet har molekyleformlen C_xH_yO_z, hvor x, y og z er naturlige tal, der skal findes.

   Molmassen af stoffet er M = (x·12,0107 + y·1,00794 + z·15,9994) g/mol. Der gælder:

      x·12,0107/M = 65,2 % ⇒ x = 0,652·M/12,0107,

      y·1,00794/M = 8,75 % ⇒ y = 0,0875·M/1,00794 og

      z·15,9994/M = 26,5 % ⇒ z = 0,265·M/15,9994.

   Når et stof spaltes vil, der gerne tilføres O eller H fra vand til de C'er, hvor bindinger brydes. Dog vil antallet af C-atomer før og efter spaltningen ikke ændres.

   Det ses af nedenstående figur, at stoffet A må have 10 C-atomer for, at C-regnskabet skal stemme.

   

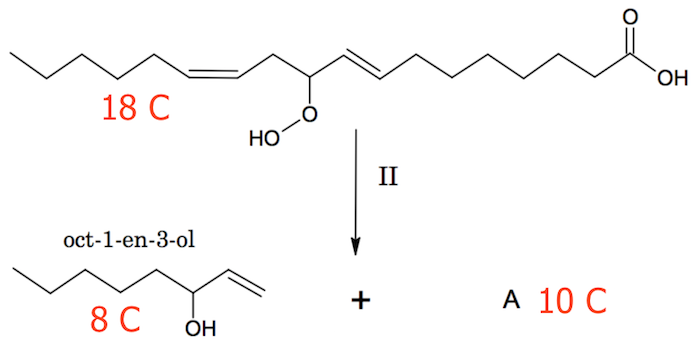
   Dette betyder, at x = 10. Heraf findes M: 10 = 0,652·M/(12,0107 g/mol) ⇒ M = 184,213 g/mol.

   Heraf fås: y = 0,0875·(184,213)/1,00794 = 16 og z = 0,265·184,213/15,9994 = 3.

   Dette giver den færdige molekyleformel: C₁₀H₁₆O₃

3. Det at A giver rødt bundfald med Fehlings væske eller sølvspejl med Tollens reagens betyder, at A indeholder en aldehyd-gruppe. Derudover indeholder A som oplyst en carboxylsyre-gruppe.

   For at antallet af H skal stemme, må A indeholde en dobbeltbinding. Det antages, at A ikke er forgrenet. Et forslag til A er vist nedenunder:

   

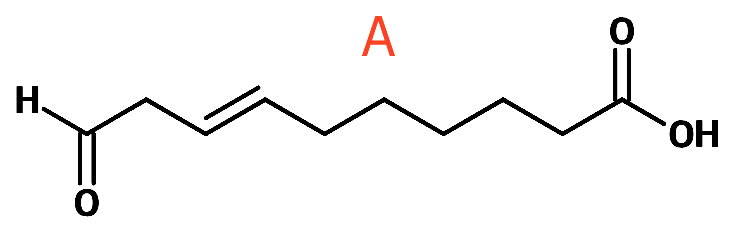
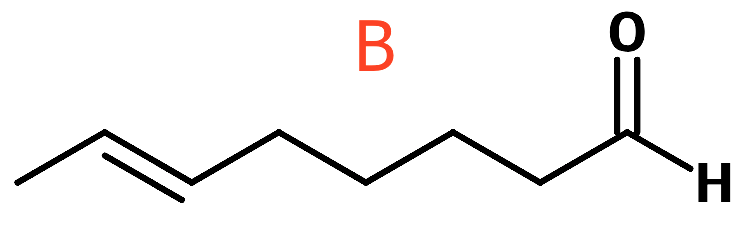
4. IR-spektret har to toppe over 1500 cm^-1. Den ene ved 1700 cm^-1 og den anden ved 3000 cm^-1. Dette er vist på figuren nendenfor.

   

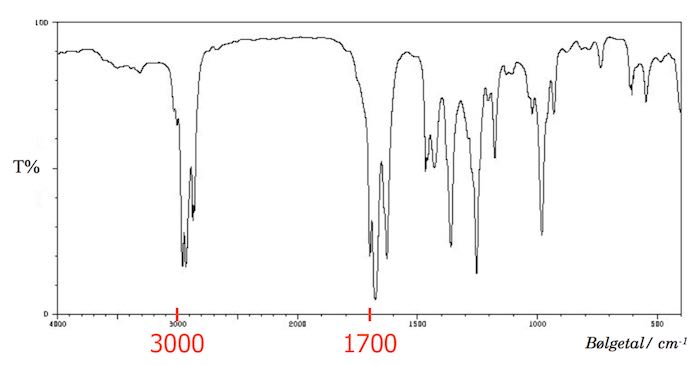
   Toppen ved 3000 cm^-1 stammer fra en C=O dobbeltbinding. Dette viser, at B er en aldehyd eller keton. Toppen omkring 3000 cm^-1 stammer fra en C=C dobbeltbinding.

   Nedenunder er vist et forslag (IUPAC-navn: (E)-oct-6-enal).

   

Svar på opgave 3: Pravastatin

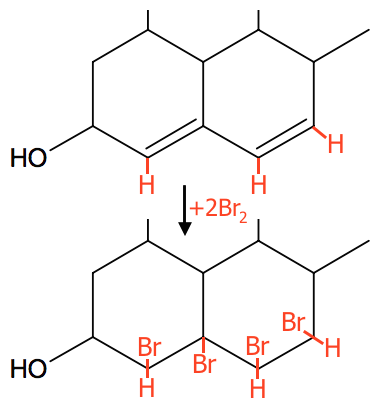
1. Der er tale om en addering. Br₂ adderes til alifatiske dobbeltbindinger (ikke dobbeltbindinger i benzenringe). Dermed bindes de enkelte Br-atomer til de C-atomer, der indgår i dobbeltbindingen.

   Der er to dobbeltbindinger i stofet. Den del af molekylet, der indeholder de to bindinger og resultatet af adderingen er vist nedenunder.

   

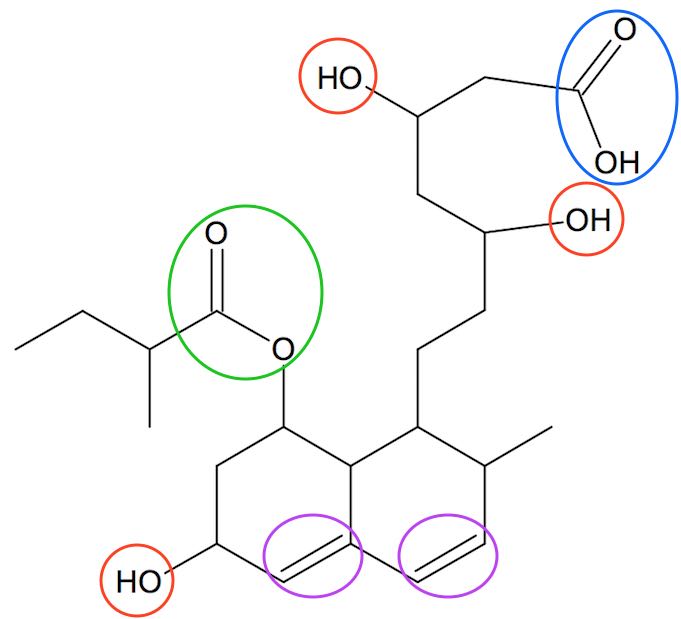
2. Der er fire funktionelle grupper i pravastatin. Disse er markeret med ringe på billedet nedenunder og de er: en carboxylsyre-gruppe (blå ring), en ester-grupper (grøn ring), tre alkohol-grupper (røde ringe) og to alken-dobbeltbindinger (lilla ringe).

   

3. Der sker en hydrolyse af esteren (spaltning ved hjælp af vand). Derved dannes en alkohol og en syre. Alkoholen sidder på det store molekyle, mens syren er det mindre molekyle, som fraspaltes. Dette er vist nedenunder.

   

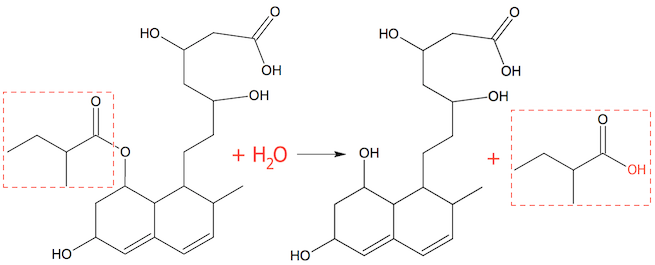
   Den fraspaltede syre hedder 2-methylbutansyre

   Forklaring: Den vigtigste funktionelle gruppe er carboxylsyre. Den længste kulstofkæde, der indeholder denne gruppe på fire kulstofatomer, dvs. syren er butansyre. Denne forbindelse er stamkæden, som nummeres fra det C-atom, der indgår i syregruppen. På plads nummer to er der en methyl gruppe (-CH₃).

   

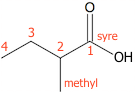
   Dette sammensættes, så stamkæden står sidst og substituenten først med angivelse af pladsering i stamkæden. Der er bindestreg mellem pladsnummer og sidekædens navn, men ikke mellem sidekædens navn og stamkædens.

4. For en nulte-ordens reaktion gælder: c(pravastatin) som funktion af tiden er lineær,

   for en første-ordens reaktion gælder: ln(c(pravastatin)) som funktion af tiden er lineær og

   for en anden-ordens reaktion gælder: (1/c(pravastatin)) som funktion af tiden er lineær.

   Man opretter lister i Ti-Nspire med tiden, c (konc), ln(c) (lnkonc) og 1/c (recikonc).

   tid:={0,7.5,13.,18.5,23.,28.,33.,39.5} ▸ {0,7.5,13.,18.5,23.,28.,33.,39.5}

   konc:={1.,0.795,0.654,0.534,0.444,0.374,0.31,0.244} ▸ {1.,0.795,0.654,0.534,0.444,0.374,0.31,0.244}

   lnkonc:=ln(konc) ▸ {0.,−0.22941,−0.42465,−0.62736,−0.81193,−0.9835,−1.1712,−1.4106}

   recikonc:=1/konc ▸ {1.,1.2579,1.5291,1.8727,2.2523,2.6738,3.2258,4.0984}

   Man laver et plot af de tre sidste lister afbildet med listen med tider som første-akseværdier. Dette giver en ret linje for ln(c) som funktion af tiden. Dvs. reaktionen er af første orden.

   ln(c) passer bedst med en ret linje, dvs. reaktionen er første-ordens. Kurven er vist nedenunder.

   

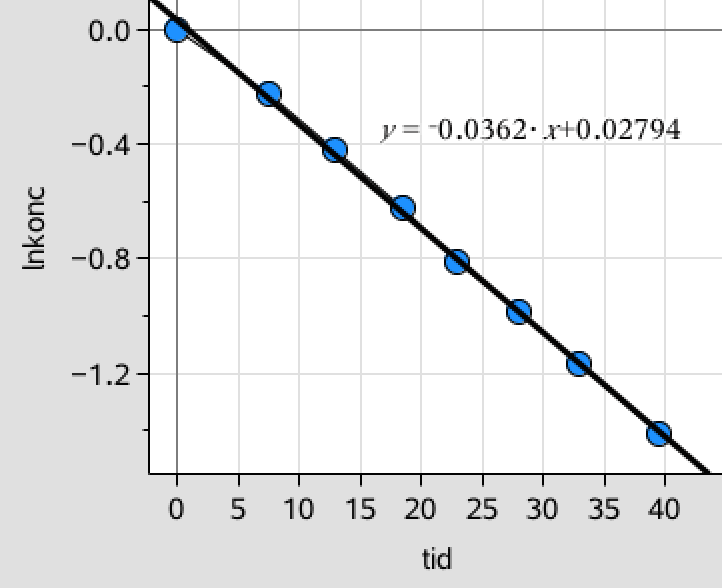
5. Formlen for halverigstiden for en førsteordensreaktion er : T_1/2 = ln(2)/ln(k).

   Man skal kende k (reaktionshastighedskonstanten) ved 400 K.

   Af grafen nedenunder ses, at y = -1363·x + 0,69, dvs. ln(k/min) = (-1363 K)·(1/T) + 0,69.

   

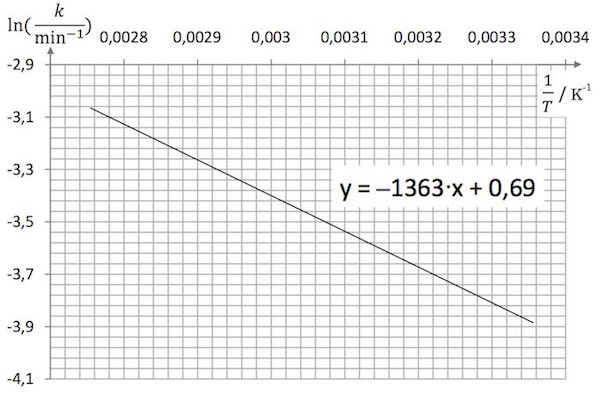
   Man får: ln(k/min) = -1363·(1/(400K)) + 0,69 ⇒ k/min = exp(−1363·(1/400)+0,69) ⇒ k = 0,066 min.

   Dvs. halveringstiden ved 400 K er T_1/2 = ln(2)/0,066 = 10,5 min.

6. Pravastatin findes på ionform som base, dvs. andelen af stof på ionform er pH-afhængig. Ionformen er mere vandopløselig og mindre opløselig i upolært opløsningsmiddel end ikke-ionformen (syreformen).

   Der gælder at jo større andel af vandopløselig form i en blanding jo mindre er K_F. Dvs. jo større pH, jo mindre K_F.

   Simvastatin mindre om pravastatin, men findes ikke på ionform og dens vandopløselighed er ikke pH-afhængig.

   Dette forklarer at K_F for pravastatin er lavere end K_F for simvastatin ved pH 7, hvor en del af pravastatin findes på baseform.

Svar på opgave 4: Saccharin

1. For at finde molmassen af saccharin sætter man de manglende C'er og H'er på stregformlen. Dette er vist nedenunder.

   

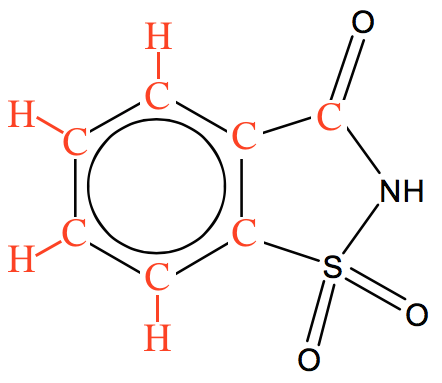
   Dette giver molekyleformlen: C₇H₅NO₃S. Heraf fås molmassen ved at gange indeksene for hvert grundstof med grundstoffets molmasse og lægge sammen. Dvs. molmassen af saccharin er:

   7·12,0107 + 5·1,0079 + 14,0067 + 3·15,9994 + 32,065 g/mol = 189,18 g/mol

2. Stofmængdekoncentrationen (C) følger formlen: C = n/V = m/(M·V), hvor

      m er massen af saccharin i opløsningen,

      M er saccharins molmasse og

      V er opløsningens rumfang.

   Man får: C = (10 g)/((183,18 g/mol)·(0,29 L)) = 0,0188 mol/L = 0,0188 M

   Dvs. stofmængdekoncentrationen af saccharin i opløsningen er 0,0188 M

3. Da pK_s ligger mellem 0 og 4, så bruger man formlen for middelstærk syre. Dvs.:

   pH = -log(-(K_s/2) + √[(K_s/2)² + K_s·c_s]), hvor

   K_s er syrestyrkekonstanten for saccharin (på syreform) = 10^2,0 og

   c_s er den formelle molære koncentration af saccharin (på syreform) = 0,0188 (enheden er M, men den udelades i formlen).

   Dette giver: pH = -log(-(10^2,0/2) + √[(10^2,0/2)² + 10^2,0·0,0188]) = 2,02

   Dvs. pH i opløsningen ved 25 °C er 2,02

4. Man skal finde x_B, dvs. basebrøken eller andelen af base i opløsningen.

   Der gælder at x_B = [B]/([S] + [B]), hvor [S] er den aktuelle koncentration af saccharin på syreform og [B] er den aktuelle koncentration af baseformen.

   Ved at dividere med [S] i tæller og nævner får man formlen: x_B = ([B]/[S])/([S]/[S] + [B]/[S]) = ([B]/[S])/(1 + [B]/[S]).

   Man kan nu finde forholdet [B]/[S] ved hjælp af pufferligningen:

   pH = pK_s + log([B]/[S]) ⇒ 1,5 = 2,0 + log([B]/[S]) ⇒ 10^-0,5 = [B]/[S] ⇒ [B]/[S] = 0,31623.

   Heraf fås: x_B = 0,31623/(1 + 0,31623) = 0,24025

   Dvs. andelen af base i opløsningen er 0,24025 = 24 %

5. Man har: m_{saccharin,tablet} = (1/20)·m_{saccharin,pulver}, hvor

      m_{saccharin,tablet} er massen af saccharin i en tablet og

      m_{saccharin,pulver} er massen af saccharin i pulver.

   Desuden har man at: m_{saccharin,pulver} = n_{saccharin,pulver}·M_saccharin, hvor

      n_{saccharin,pulver} er stofmængden af saccharin i pulveret og

      M_saccharin er molmassen af saccharin.

   Ved fældningen gælder, at: n_{saccharin,pulver} = n_AgNO3,tilsat - n_{AgNO3,overskud}, hvor

      n_AgNO3,tilsat er antal mol tilsat AgNO₃,

      n_{saccharin,pulver} er antal mol saccharin i pulveret og

      n_{AgNO3,overskud} er antal mol af AgNO₃ i opløsningen efter fældningen.

   Der gælder endvidere: n_{AgNO3,overskud} = n_KSCN,tilsat, hvor

      n_KSCN,tilsat er antal mol tilsat KSCN ved titrering.

   Man har videre: n_KSCN,tilsat = C_KSCN·V_KSCN,tilsat, hvor

      C_KSCN er stofmængdekoncetrationen af KSCN i titrator og

      V_KSCN,tilsat er det tilsatte rumfang af titrator ved omslag.

   Ligeledes gælder, at n_AgNO3,tilsat = C_AgNO3·V_AgNO3,tilsat, hvor

      C_AgNO3 er stofmængdekoncentrationen af AgNO₃ i den tilsatte opløsning og

      V_AgNO3,tilsat er rumfanget af tilsat AgNO₃ ved fældningen.

   Dette giver: m_{saccharin,tablet} =

      (1/20)·m_{saccharin,pulver} =

      (1/20)·n_{saccharin,pulver}·M_saccharin =

      (1/20)·(n_AgNO3,tilsat - n_{AgNO3,overskud})·M_saccharin =

      (1/20)·(n_AgNO3,tilsat - n_KSCN,tilsat)·M_saccharin =

      (1/20)·(C_AgNO3·V_AgNO3,tilsat - C_KSCN·V_KSCN,tilsat)·M_saccharin =

      (1/20)·((0,0818 M)·(0,02 L) - (0,0412 M)·(0,00281 L))·(183,18 g/mol) =

      0,0139 g.

   Dvs. massen af saccharin i en tablet er 0,0139 g = 13,9 mg