Svar på opgave 1:

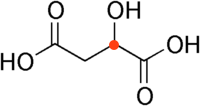
1. Æblesyre har et asymmetrisk kulstofatom (vist med rødt). Det OH, der sidder på dette c-atom kan enten ligge over eller under tegningens plan.

   

   (Wikipedia)

2. Stoffet har to funktionelle grupper: to syre gruppe og en OH-gruppe (hydroxyl-gruppe). Syregrupperne har den højeste prioritet. Den længste kulstofkæde der indeholder syregrupperne er butansyre og giver dermed sídste del af navnet "-butandisyre".

   Hydroxylgruppen skal nummereres ud fra den nærmeste syregruppe, så dens nummer bliver så lavt som muligt. Det giver tallet 2 og navnet på stoffet bliver: 2-hydroxydibutansyre.

3. Kan ikke besvares da bilag mangler.

4. pKs for den ene carboxylsyre i æblesyre er 3,4. Dette indsættes i formlen for pH af en svag syre: pH = 0,5·(pKs-log[cs]) = 0,5·(3,4- log(0,016)) = 2,6

5. Kan ikke besvares da bilag mangler, men antag at der er tale om en gaschromatografisk bestemmelse. Her bestemmer man stoffet ud fra en liste over retentionstider, dvs. man tager en række kendte stoffer og måler hvor længe de er om at komme gennem gaschromatografen. Denne liste sammenlignes et ukendte stof, som man ønsker at bestemme.

   Koncentrationen af stoffet kan måles som arealet under den top, som stoffet danner med den graftegner, der hører til gaschromatografen.

   I dette tilfælde ved man tilsyneladende at stoffet er æblesyre og skal måle arealet.

6. Kan ikke besvares da bilag mangler, men ordet retentionstid hentyder som før nævnt nok til gaschromatografi. Det der har betydning er vandopløseligheden. Vinsyre er mere vandopløseligt end ravsyre og tilbageholdes derfor mindre i gaschromatografkolonnen og har derfor kortere retentionstid.

   

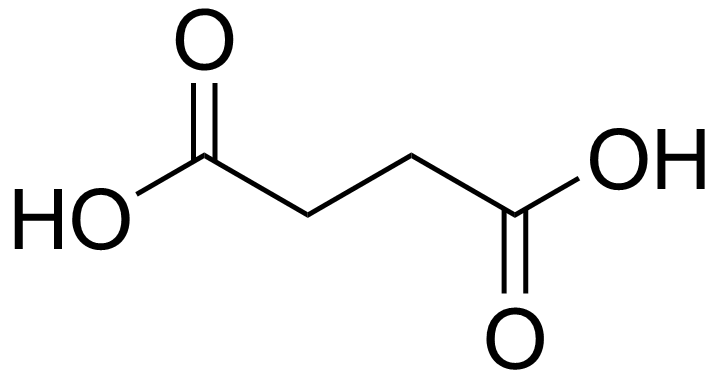
   Ravsyre (Wikipedia).

   

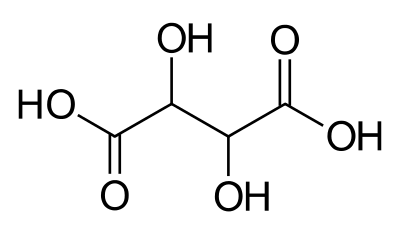
   Vinsyre (Wikipedia).

Svar på opgave 2:

1. Der er to funktionelle grupper: en ester og en phenol som vist nedenunder.

   

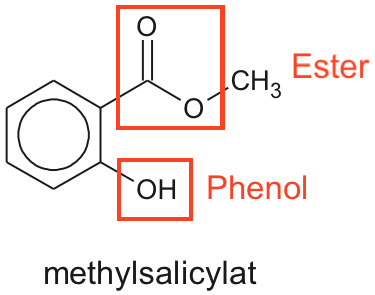
   (Man kan også sige hydroxylgruppe i stedet for phenolgruppe. Alkohol giver næppe fuld point, da det kræver, at OH er bundet til en alifatisk kulstofkæde og ikke en aromatisk som her).

2. Der er tale om en kondensations-reaktion, idet H₂O fraspaltes.

   Koncentreret svovlsyre binder sig til H₂O og forhindrer det i at reagere med methylsalicylat, så ligevægten forskydes mod højre.

3. Man starter med at undersøge hvilken reaktant, som er i underskud. Denne reaktant bestemmer mængden af dannet stof. Man bestemmer antal mol for hver reaktant:

   Antal mol salisylsyre: masse/molmasse = 9,01 g/(138,121 g/mol) = 0,06523 mol

   Antal mol methanol: masse/molmasse = (antal mL)·(densitet)/molmasse = (25 mL)·(0,7914 g/mL)/(32,04 g/mol) = 0,61751 mol

   Dvs. salisylsyre er i underskud og bestemmer, hvor mange mol methylsalicylat, der kan dannes. Da salisylsyre og methylsalicylat optræder i forholdet 1:1 i reaktionsligningen gælder, at antal mol reageret salisylsyre = antal mol dannet methylsalicylat = 0,06523 mol. Da molmassen af methylsalicylat er 152,15 g/mol får man, at det teoretiske udbytte er:

   (0,06523 mol)·(152,15 g/mol) = 9,93 g

Svar på opgave 3:

1. Ligevægstsbrøken er K_p = (p_NO2)²/p_N2O4, hvor p er partialtryk.

2. Man finder summen af dannelsesentalpier for reaktanter og trækker den fra summen af dannelsesentalpierne for produkter.

   Reaktanter: ΔH^o for N₂O₄ er 11,1 kJ/mol

   Produkter: ΔH^o for NO₂ er 33,2 kJ/mol

   ΔH^o for reaktionen er 2·33,2 kJ/mol - 11,1 kJ/mol = 55,3 kJ/mol

   Det at ΔH^o for reaktionen mod højre er positiv betyder, at der bruges varme, når ligevægten forskydes mod højre, mens der skabes varme, når den forskydes mod venstre.

   Hvis der tilføres varme vil den derfor forskydes mod højre for at forbruge noget af den tilførte varme (i følge le Chateliers princip).

3. For at beregne K_p ved en anden temperatur end 25 ^oC bruger man van't Hoff ligningen:

   ln(K_p) = -ΔH^o/(R·T) + ΔS^o/R, hvor ΔH^o er fundet ovenfor.

   ΔS^o for N₂O₄ er 304,4 J/(mol·K) og ΔS^o for NO₂ er 240,1 J/(mol·K).

   ΔS^o for reaktionen er 2·240,1 J/(mol·K) - 304,4 J/(mol·K) = 175,8 J/(mol·K)

   Man får følgende (husk at entalpien er opgivet i kJ, og at temperaturen i Kelvin er 273 + 50 = 323):

   ln(K_p) = -[55,3 kJ/mol]/[8,314 (J/(mol·K))·323 K] + [175,8 J/(mol·K)]/[8,314 J/(mol·K)] ⇒

   ln(K_p) = -[55300]/[8,314·323] + [175,8]/[8,314] ⇒

   ln(K_p) = −20,593 + 21,145 = 0,552 ⇒ K_p = e^0,552 = 1,74

4. Lige efter indsprøjtningen indeholder beholderen kun N₂O₄. Dette giver følgende, hvor n, m og M er henholdesvis stofmængde, masse og molmasse af N₂O₄:

   p = n·R·T/V = [m/M]·R·T/V = [(0,52 g)/(92,01 g/mol)]·[0,08314 bar·L/(mol·K)]·(323 K)/(2 L) =

   (0,52/92,01)·(0,08314 bar)·323/2 = 0,0759 bar

5. Hver gang der dannes x mol NO₂, forsvinder der (1/2)·x mol N₂O₄. Da partialtrykket af de enkelte stoffer er proportionalt med deres stofmængde (p = n·R·T/V hvor R·T/V er konstant), får man at P(N₂O₄) = 0,0759 bar - (1/2)·P(NO₂).

   Ved ligevægt får man derfor ligningen: [P(NO₂)]²/[0,0759 bar - (1/2)·P(NO₂)] = 1,74 bar

   Denne ligning løses med hensyn til P(NO₂), og man får at P(NO₂) = 0,132 bar ved ligevægt.

   Ti-Nspire: solve(p²/(0.0759-0.5*p)=1.74 and p>0,p) ▸ p=0.1318

   Heraf finder man, at P(N₂O₄) = 0,0759 bar - (1/2)·(0,132 bar) = 0,099 bar ved ligevægt

   Dvs. ligevægtspartialtrykkene er P(N₂O₄,ligevægt) = 0,099 bar og P(NO₂,ligevægt) = 0,132 bar

Svar på opgave 4:

1. CH₃CH₂CH₂CH₂CH=CH₂ + I₂ → CH₃CH₂CH₂CH₂CHICH₂I

   Med stregformel:

   

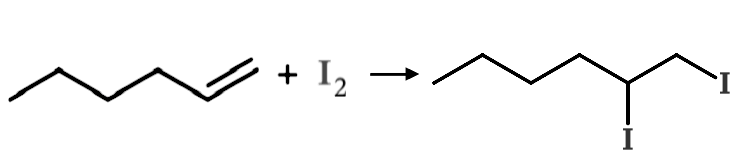
2. Hvis reaktionen er af første orden med hensyn til koncentrationen af diiod, skal der gælde at koncentrationen kan skrives på formen: [I₂] = C₀·e^k·t, hvor C₀ er startkoncentrationen af diiod.

   Hvis reaktionen derimod er af anden orden skal der gælde, at koncentrationen som funktion af tiden kan skrives: [I₂] = 1/(k·t + 1/C₀)

   I det første tilfælde vil en afbildning af logaritmen til koncentrationen af diiod mod tiden give en ret linje. I det andet tilfælde vil en afbildning af den omvendte eller reciprokke til koncentrationen af diiod mod tiden give en ret linje.

   Man opretter en liste over tider i Ti-Nspire:

   tid:={0,2000,4000,6000,8000} ▸ {0,2000,4000,6000,8000}

   Man opretter derefter en liste over koncentrationer:

   konc:={0.02,0.0128,0.0094,0.0075,0.0062} ▸ {0.02,0.0128,0.0094,0.0075,0.0062}

   Endelig oprettes en liste over logaritmen til koncentrationerne og en liste over en divideret med værdier af koncentrationerne:

   log_konc:=log(konc,10) ▸ {−1.69897,−1.89279,−2.02687,−2.12494,−2.20761}

   rec_konc:=1/konc ▸ {50.,78.125,106.383,133.333,161.29} (reciprokke koncentrationer)

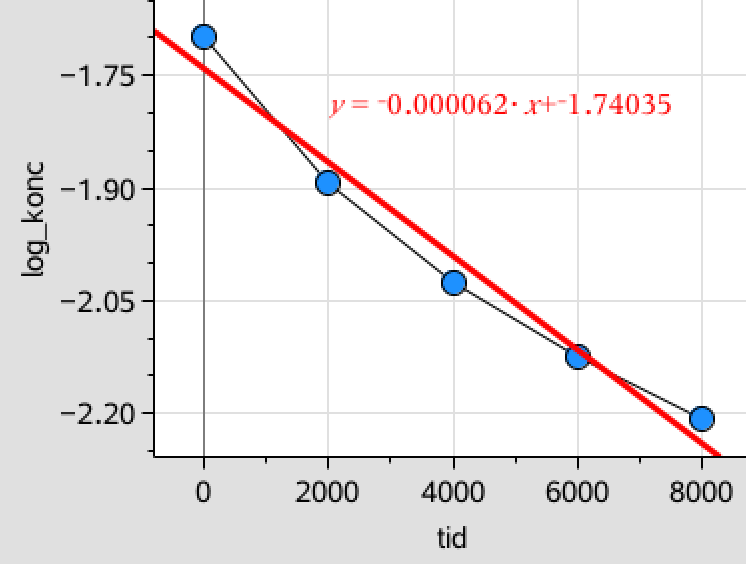
   Man afbilder logaritmen til koncentratioernerne af diiod som funktion af tiden. (Man kan også sige laver et plot af logaritmen til koncentrationen mod tiden). Til afbildningen tilføjer man en lineær regressionslinje, der er vist med rødt. Det er vist nedenunder på Figur 1:

   

   Tilsvarende afbilder man den reciprokke værdi af koncentrationerne af diiod som funktion af tiden. Her indlægges ligeledes en rød lineær regressionslinje. Dette er vist nedenunder på Figur 2:

   

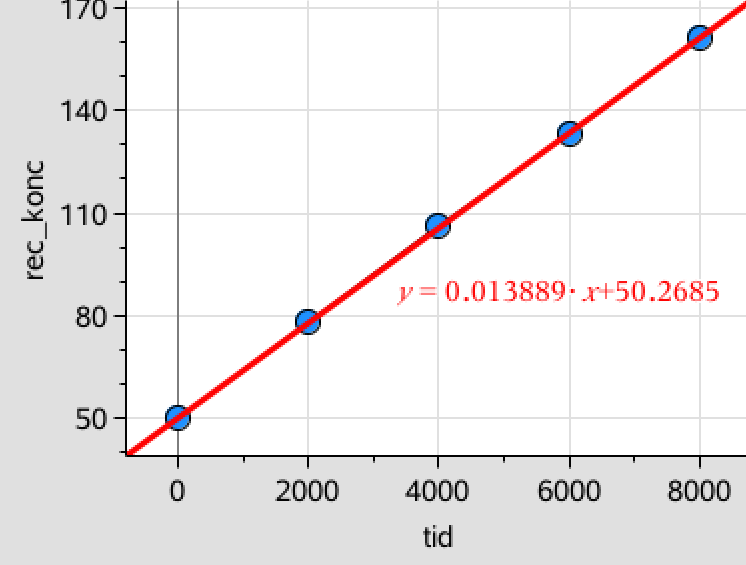
   Som det ses er det regressionslinjen for een divideret med koncentrationen af diiod som funktion af tiden (Figur 2), der passer bedst til en ret linje og reaktionen er dermed af anden orden

3. Af regressionslinje på figur 2 fremgår det at 1/[I₂] = 0,0139·t + 50,27. Ved at indsætte t = 3500 s får man:

   1/[I₂] = (0,0139·3500 + 50,27) M^-1 ⇒ [I₂] = 1/(0,0139·3500 + 50,27) M = 0,0101 M

   (Dette passer også med tabellen i opgaven, hvor man kan se, at koncentrationen skal ligge mellem 0,0094 M, der er værdien for t = 4000 s og 0,0128 M, der er værdien for t = 2000 s).

4. Man kan følge koncentrationen af diiod ved hjælp af spektrofotometri. Jo mindre lys der absorberes af den rødbrune blanding, jo lavere er koncentrationen af dioiod, og jo længere er reaktionen forløbet mod højre.

   (Man skal bruge blåt lys til at måle med, idet blå er kontrastfarven til orange eller rødbrun. Man skal muligvis bruge et særligt instrument, der kan måle løbende uden at man behøver at udtage prøver, der dels mindsker reaktionsblandingen, dels når at reagere videre inden koncentrationen er målt).