Klik på en opgave for at se, hvordan den løses.
Et elektrisk varmelegeme tilføres en strømstyrke på 0,10 A og pålægges en spænding på 110 V.
-
Hvilken effekt afgiver varmelegemet?
-
Hvor meget varmeenergi afgives fra varmelegemet på 3 minutter?
-
Hvor meget energi afgives af varmelegemet undervejs?
Varmelegemet opvarmer 175 g vand fra 20,0 °C til kogepunktet og får derefter halvdelen af vandet til at fordampe.
Svar på opgave 1:
-
Effekten (P) er I·U, hvor I er strømstyrken og U er spændingen.
Med tallene indsat får man, at P = (0,10 A)·(110 V) = 11 W
-
Den afsatte energi, Q = P·Δt, hvor Δt er tiden i sekunder.
Man får: Δt = (3 min)·(60 s/min) = 180 s.
Dvs den afgivne energi er: (11 W)·(180 s) = 1980 J = 1,98 kJ
-
Der skal dels bruges varme til opvarming af vandet (Qv), dels til fordampning (Qf).
Vands kogepunkt ved 1 atm er 100 °C.
Vands specifikke varmekapacitet er cv = 4,18 kJ/(K·kg).
Vands fordampningsvarme Lf = 2257 kJ/kg ved 100 °C
Der gælder: Qv = ΔT·mv·cv, hvor ΔT er ændringen i vandets temperatur under opvarmning og mv er massen af opvarmet vand.
Heri indsættes tallene: Qv = [(100 - 20,0) K]·(0,175 kg)·(4,184 kJ/(K·kg)) = 80,0·0,175·4,184 kJ = 58,6 kJ
For fordampningen får man: Qf = Lf·mf, hvor mf er massen af fordampet vand.
Heri indsættes tallene: Qf = (2257 kJ/kg)·(0,175/2 kg) = 2257·0,175/2 kJ = 197 kJ
Den samlede energi for opvarmning og fordampning bliver dermed: 58,6 kJ + 197 kJ = 256 kJ
15,0 g af et fast stof med temperaturen 25,0 °C nedsænkes i 125 g vand med temperaturen 50,0 °C. Efter et stykke tid indstiller der sig en blandingstemperatur for vandet og stoffet, der i mellemtiden er smeltet helt.
For stoffet gælder:
-
Smeltepunkt: 35,0 °C.
-
Specifik smeltevarme: 76,0 kJ/kg.
-
Specifik varmekapacitet på fast form: 350 J/(K·kg).
-
Specifik varmekapacitet på flydende form: 410 J/(K·kg).
-
Hvad er blandingstemperaturen for stof og vand?
Svar på opgave 2:
-
Den varme, som stoffet modtager (Qs), er lig med den varme, som vandet afgiver (Qv).
Qs kan deles i tre dele: Qs,1, der er den varme, som stoffet modtager fra 25,0 °C til smeltepunktet, Qs,2, der er stoffets smeltevarme og Qs,3, der er den varme, som det flydende stof modtager efter smeltning.
Qs,1 = (35,0 °C - 25,0 °C)·cs,1·ms = (10,0 °C)·[350 J/(°C·kg)]·(0,015 kg) = 10·350·0,015 J = 52,5 J, hvor cs,1 er den specifikke varmekapacitet for stoffet på fast form og ms er massen af stof.
Qs,2 = ms·Ls = (0,0150 kg)·(76,0 kJ/kg) = 1140 J, hvor Ls er stoffets specifikke smeltevarme = 76,0 kJ/kg.
Qs,3 = (T - 35,0 °C)·cs,3·ms = (T - 35 °C)·[410 J/(°C·kg)]·(0,125 kg) = (51,25 J/°C)·T - 1793,75 J, hvor T er blandingstemperaturen i °C og cs,3 er den specifikke varmekapacitet for flydende stof = 410 J/(K·kg).
I alt fås: Qs = 52,5 J + 1140 J + (51,25 J/°C)·T - 1793,75 J = (51,25 J/°C)·T - 601,25 J
Qv = (50,0 °C - T)·cv·mv = (50,0 °C - T)·[4,18 kJ/(°C·kg)]·(0,125 kg) = 26125 J - (522,5 J/°C)·T, hvor cv er den specifikke varmekapacitet for vand, der har tabelværdien 4,18 kJ/(°C·kg), og mv er massen af vand = 0,125 kg.
Qs = Qv ⇒ (51,25 J/°C)·T - 601,25 J = 26125 J - (522,5 J/°C)·T ⇒ T = 46,6 °C
Dvs. blandingstemperaturen er 46,6 °C
Lys med bølgelængden 490 nm udsendes fra en galakse. Ved jorden observeres strålingen som en spektrallinje for lys med bølgelængden 550 nm.
-
Hvad er frekvensen for det observerede lys?
-
Hvad er rødforskydningen af lyset fra galaksen?
-
Hvad er Jordens afstand til galaksen?
Svar på opgave 3:
-
Der gælder følgende formel for frekvensen, f, af lysets: f = c/λ, hvor c er lysets hastighed og λ er lysets bølgelængde. Her er:
c = 3,00·108 m/s og λ = 550 nm = 550·10-9 m = 5,50·10-7 m.
Dvs. frekvensen af det observerede lys er: (3,00·108 m/s)/(5,50·10-7 m) = 5,45·1014 s-1 (s-1 = Hz)
-
Rødforskydningen, z, er defineret som:
z = (λobs - λud)/λud, hvor
λobs er bølgelængden for den observerede stråling og
λud er bølgelængden af den udsendte stråling.
Man får at rødforskydningen er: (550 nm - 490 nm)/(490 nm) = 0,122
-
Afstanden, D, til galaksen findes ved hjælp af Hubbles lov, når man kender rødforskydningen og denne ikke er for stor. Her antages, at Hubbles lov er gyldig.
D ≈ z·c/H, hvor
H er Hubbles konstant = 70,0 km/(s·Mpc) = 70,0·103 m/(106·3,085·1016 m·s)) = 2,27·10-18 s-1.
Dette giver følgende afstand til galaksen: 0,122·(3,00·108 m/s)·/(2,27·10-18 s-1) = 1,62·1025 m (eller 1,71·109 lysår)
-
Ved hvilken bølgelængde har stjernens lys sin maksimale intensitet?
-
Hvad er stjernens effektive overfladetemperatur?
-
Hvad er effekten af stjernens lys pr. kvadratmeter ved jordoverfladen?
En stjerne har den effektive overfladetemperatur 13,2·103 K.
En anden stjerne med radius 3,05·109 m har en udstrålet effekt på 7,96·1027 W og befinder sig 12,4 lysår fra Jorden.
Svar på opgave 4:
-
Man bruger Wiens forskydningslov:
Ved hjælp af Wiens forskydningslov får man:.
λmax = (2,898·10-3 m·K)/T, hvor
λmax er den bølgelængde, der giver en maksimale intensitet og
T er stjernens effektive overfladetemperatur = 1,32·104 K
Dvs. den bølgelængde, der giver den største intensitet, er (2,898·10-3 m·K)/(1,32·104 K) =
2,195·10−7 m = 220 nm
-
Man bruger Stefan-Boltzmanns lov for at finde den effektive overfladetemperatur (T) af stjernen:
L = 4·π·R2·σ·T4 ⇒ T = 4√[L·R-2·(4·π·σ)-1], hvor
L er stjernen luminositet (udstrålede effekt i W) = 7,96·1027 W,
R er stjernens radius = 3,05·109 m,
σ er Stefan-Boltzmanns konstant = 5,6704·10-8 W·m-2·K-4 og
Heraf fås stjernens effektive overfladetemperatur er:
4√[(7,96·1027 W)·(3,05·109 m)-2·(4·π·5,6704·10-8 W·m-2·K-4)-1] = 5,89·103 K
-
Man bruger afstandskvadratloven til at finde effekten pr m2 (I) af stjernens lys ved jordoverfladen:
I = L/(4·π·R2), hvor
R er afstanden fra stjernen til jorden = 12,4 lysår = 12,4·(9,461·1015 m) = 1,17·1017 m og
L er stjernens luminositet eller udstrålede effekt = 7,96·1027 W.
Det forudsættes, at stjernen er kugleformet, lyser ens i alle retning, og at der ikke sker tab af lys i Jordens atmosfære.
Man får, at effekten af stjernens lys pr. m2 på jordoverfladen er:
(7,96·1027 W)/(4·π·(1,17·1017 m)2) = 4,63·10-8 W·m-2
Opskriv reaktionsligningerne for følgende:
-
Alfa-henfald af Cl-32
-
Beta-minus henfald af N-18
-
Henfald af Zn-63 ved elektronindfangning
Svar på opgave 5:
-
Ved alfa-henfald afgives en helium-kerne, som forlader atomet. Den positive ladning på He-kernen udlignes med den negative på P-28 gennem kemiske reaktioner, som ikke er medtaget. Den fysiske reaktion er vist nedenunder:
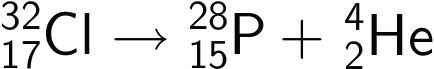
Man gør prøve med hensyn til nukleontal (de øverste tal), ladning (de nederste tal):
Nukleontal: venstre: 32, højre: 28 + 4 = 32.
Ladning: venstre: 17, højre: 15 + 2 = 17.
Der dannes også energi, hvilket dog ikke er medtaget.
-
Ved beta-minus henfald afgiver en af kernens neutroner en elektron, som forlader atomet og efterlader en ekstra proton i kernen. Samtidig dannes en antineutrino, der ligesom elektronen er en lepton. Reaktionsskemaet er vist nedenunder:

Man gør prøve med hensyn til nukleontal (de øverste tal), ladning (de nederste tal) og leptontal (elektron = +1 og antineutrino = -1):
Nukleontal: venstre: 18, højre: 18 + 0 = 18.
Ladning: venstre: 7, højre: 8 - 1 = 7.
Leptontal: venstre: 0, højre: 1 - 1 = 0.
-
Ved elektronindfangning optager atomets kerne en elektron fra atomets elektronsky. Derved omdannes en af kernens protoner til en neutron. Samtidig dannes en neutrino, der ligesom elektronen er en lepton. Reaktionsskemaet er vist nedenunder:

Man gør prøve med hensyn til nukleontal (de øverste tal), ladning (de nederste tal) og leptontal (elektron = +1 og neutrino = +1):
Nukleontal: venstre: 63 + 0 = 63, højre: 63.
Ladning: venstre: 30 - 1 = 29, højre: 29.
Leptontal: venstre: 1, højre: 1.
Th-228 med startaktiviteten 2,65·104 Bq henfalder.
-
Hvor længe går der før aktiviteten er faldet til 1,00·104 Bq?
-
Hvor mange Th-228 kerner henfalder de første 5 år?
Svar på opgave 6:
-
Man bruger formlen for aktiviteten, A, som funktion af tiden, t, af radioaktivt henfald:
A(t) = A(0)·0,5t/T, hvor
A(0) er aktiviteten fra start = 2,60·105 s-1 og
T er halveringstiden for Th-228, som slås op til 1,913 år.
Man skal have fælles enhed for startaktivitet og halverigstid og vælger at regne halveringstiden om til sekunder:
T = 1,913 år = (1,913 år)·(3600·24·365,25 s/år) = 6,037·107 s.
Tallene indsættes i formlen, og man løser ligningen A(t) = 1,00·104 s-1 med hensyn til t:
solve(2.60·104·0,5t/(6.037·107)=1.00·104,t) ▸ 8.32207·107 (Ti-Nspire)
Dvs. der går 8,32·107 s (eller 2,64 år) før aktiviteten er faldet til 1,00·104 Bq.
-
Aktiviteten er antal henfald pr. sekund. Når man skal finde antallet af henfald for de første 5 år, så skal man integrere A(t) fra t = 0 til t = 5 år = (5 år)·(3600·24·365,25 s/år) = 1,578·108 s.
Man får: integral(2.6·104·0.5t/(6.037·107),t,0,1.578·108) ▸ 2.264·1012 (Ti-Nspire)
Dvs. i løbet af de første 5 år sker der: 2,26·1012 henfald
En bold kastes op i luften med en vinkel på 50,0° i forhold til vandret og flyver henover et jævnt terræn. Den starter sin bevægelse i en højde af 1,50 m over jorden og lander på jorden 18,0 m væk.
-
Hvad er boldens begyndelsesfart?
-
Hvad er boldens stighøjde?
Svar på opgave 7:
Der ses bort fra vindmodstand og boldens størrelse, dvs. boldens bevægelse er lig med dens massemidtpunkts. Kastet foregår i et to-dimensionelt koordinatsystem med nulpunkt (0;1,5), positiv x-retning i kasteretningen og positiv y-retning opad.
-
Man opstiller kasteparablen (enhed for x og y er meter):
y(x) = −0,5·g·v0-2·(cos(α))-2·x2 + tan(α)·x + y(0) ⇒
y(x) = −0,5·9,82·v0-2·(cos(50,0°))-2·x2 + tan(50,0°)·x + 1,50 ⇒
y(x) = −11,88·v0-2·x2 + 1,192·x + 1,50.
Heraf findes v0 ved at løse ligningen y(18) = 0 og vælge den positive løsning. (y = 0 er jordoverfladen.)
solve(−11,88*v0-2*182+1,192*18.+1.5=0,v0) ▸ v0=−12.95 or v0=12.95
Dvs. boldens begyndelsesfart er 13,0 m·s-1
-
Boldens stighøjde, h, er forskellen mellem dens starthøjde og dens største højde over jorden. Der gælder:
h = v02·sin2(α)/(2·g) = (13,02 m·s-1)·sin2(50,0°)/(2·9,82 m·s-2) = 5,0496 m
Dvs. stighøjden er 5,05 m
En faldskærmsudspringer med massen 70,0 kg svæver lodret nedad med åben skærm og en fart af 5,0 m/s. Faldskærmens åbning er cirkelformet med en radius på 2,5 m.
-
Hvad er faldskærmens formfaktor?
Svar på opgave 8:
-
Der ses bort fra tyngdekraften på faldskærmen samt luftmodstanden på faldskærmsudspringeren.
Formfaktoren, c, findes ved hjælp af formlen: F = 0,5·ρ·c·A·v2, hvor
F er luftsmodstandskraften på faldskærmen,
ρ er luftens densitet ved 20 °C = 1,2 kg·m-3,
A er faldskærmens areal vinkelret på luftstrømmen = π·2,52 m2 = 19,635 m2 og
v er luftens fart i forhold til faldskærmen = 5,0 m·s-1.
Når faldskærmen bevæger sig nedad med konstant fart, så er den resulterende kraft på den 0 og dermed er luftmodstandskraften på faldskærmen lig med tyngdekrafen på udspringeren.
Tyngekraftens størrelse er lig med massen af faldskærmsudspringeren gange tyngdeaccelrationen, dvs. der gælder:
(70 kg)·(9,82 m·s-2) = 0,5·(1,2 kg·m-3)·c·(19,635 m)·(5,0 m·s-1)2
Denne ligning løses med hensyn til c i Ti-Nspire:
solve(70*9.82=0.5*1.2*c*19.635*5.2,c) ▸ c=2.3339
Dvs faldskærmens formfaktor er 2,3
En benzindrevet bil kører med konstant acceleration fra stilstand til en fart på 100 km/t på 11,0 s.
-
Hvor langt kører bilen i løbet af denne tid? (Bilens masse regnes for konstant)
-
Hvad er bilens fart ved tidspunktet 12,0 s?
En batteridrevet bil med massen 800 kg kører med konstant effekt på 100 kW i 12,0 s. Ved tidspunktet 12,0 s er bilens acceleration 6,00 m/s2.
Svar på opgave 9:
-
Idet s0 sættes til 0 og v0 = 0, så har man følgende formler for strækningen og farten som funktion af tiden:
s(t) = 0,5·a·t2
v(t) = a·t
Man skal finde s(11 s).
Man ved, at v(11 s) = 100 km/t = 100·(1000 m)/(3600 s) = 27,78 m/s.
Heraf findes a: v(11,0 s) = a·(11,0 s) = 27,78 m/s ⇒ a = (27,78 m/s)/(11,0 s) = 2,53 m/s2.
Dvs. den tilbagelagte strækning efter 11 s er: 0,5·(2,53 m/s2)·(11,0 s)2 = 153 m
-
Ved konstant effekt, P, gælder: P = F(t)·v(t) = m·a(t)·v(t) ⇒ v(t) = P/[m·a(t)].
For tidspunktet t = 12,0 s får man:
v(12,0 s) = (100 kW)/[(800 kg)·a(12,0 s)] = (100 kW)/[(800 kg)·(6,00 m/s2)] = 100000/(800·6,00) m/s =
20,8 m/s (eller 74,9 km/t)
En kugle hænger i en snor fra loftet og foretager en jævn vandret cirkelbevægelse med radius er 1,15 m. Vinklen mellem snor og lodret er 60°.
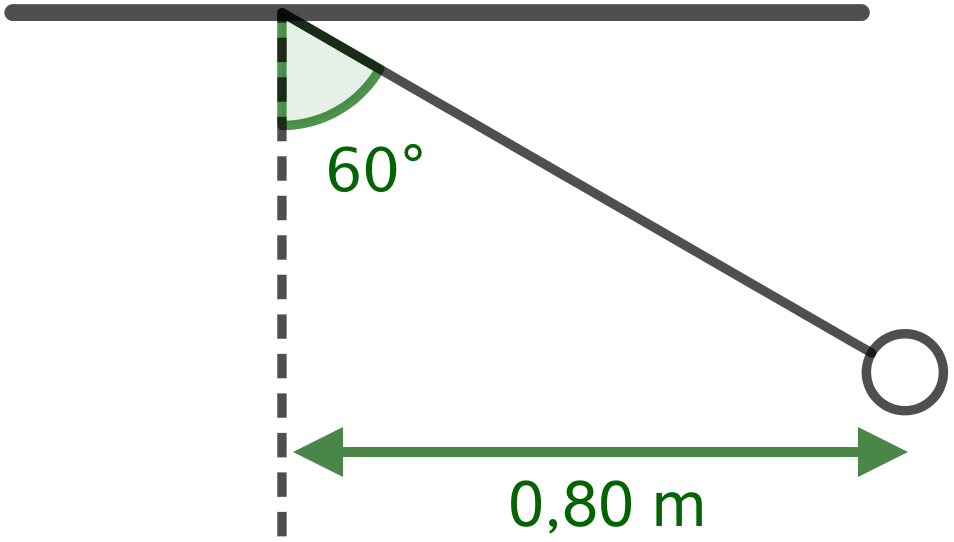
-
Hvad er kuglens fart?
Svar på opgave 10:
-
Nedenfor er vist et kraftdiagram for kuglen. FT er tyngdekraften, FS er snorkraften og FC er den resulterende kraft nemlig centripetalkraften.
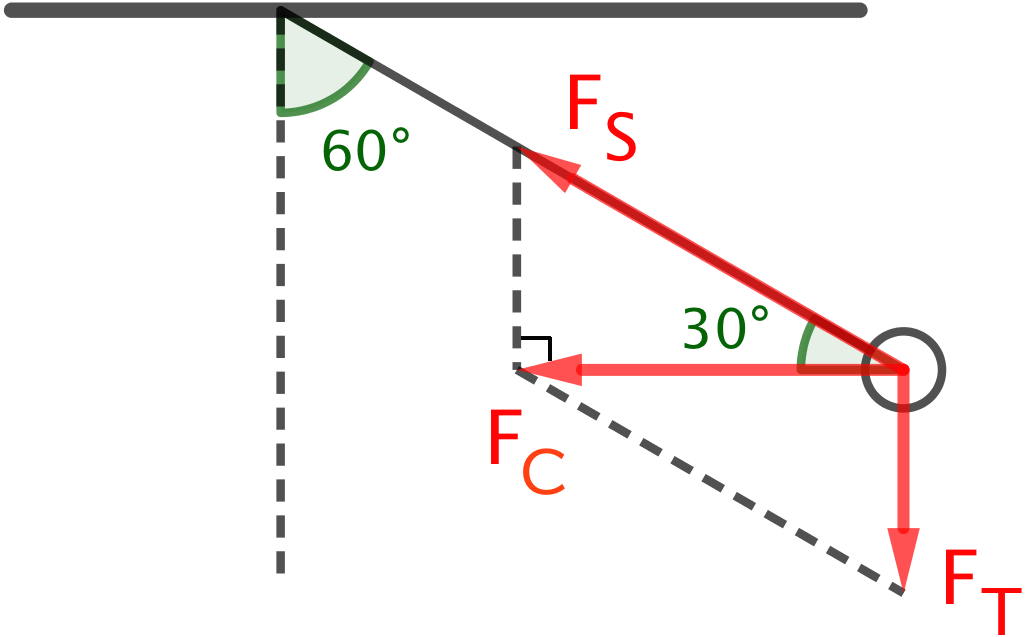
Der gælder følgende formel for centripetalkraften:
|FC| = m·v2/r, hvor
m er massen af kuglen (går ud),
v er farten af kuglen (skal findes) og
r er radius af cirkelbevægelsen = 1,20 m.
Desuden gælder formlen: tan(30°) = |FT|/|FC| ⇒ |FC| = |FT|/tan(30°) ⇒ |FC| = m·g/tan(30°), hvor g er tyngdeaccelerationen.
Samlet giver de to formler for FC: m·v2/r = m·g/tan(30°) ⇒ v2 = g·r/tan(30°) ⇒ v = √[g·r/tan(30°)].
Dvs. kuglens fart er: √[(9,82 m/s2)·(1,20 m)/tan(30°)] = 4,52 m/s
En et-trinsraket accelererer lodret opad så længe, at der er brændstof. På et tidspunkt er brændstoffet brugt op og raketten fortsætter flyvningen nu kun påvirket af tyngdekraft og luftmodstand. Raketten påvirkes ikke af vind sidelæns.
Nedenunder er vist et diagram af rakettens fart, v, som funktion af tiden, t. Positiv bevægelsesretning for raketten er opad.
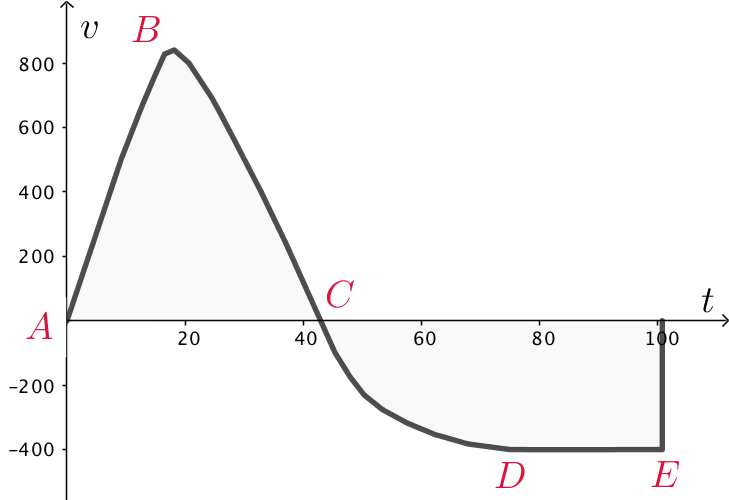
På diagrammet er fem punkter markeret med bogstaverne A, B, C, D og E. Arealet under kurven er gråt.
-
Forklar hvad der sker ved de fem bogstaver A, B, C, D og E.
-
Hvad gælder for den del af det grå areal, der ligger over x-aksen sammenlignet ved den del, som ligger under?
-
Hvor højt når raketten?
Det samlede (grå) areal under kurven er 39.000 m.
Svar på opgave 11:
-
Generelt: når kurven er over x-aksen, så bevæger raketten sig opad, mens den bevæger sig nedad, når kurven er under.
A er start. Mellem A og B er kurven en ret linje, hvilket svarer til konstant acceleration. Da luftmodstanden stiger med farten, så man skulle forvente, at farten i stedet nærmede sig en vandret linje, men da luften samtidig bliver tyndere, så forbliver gnidningskraften ens og accelerationen dermed konstant.
B er det sted, hvor brændstoffet slipper op. Her når farten sit maksimum. Raketten bevæger sig opad, men tyngdekraft og luftmodstand bremser raketten.
C er toppunktet. Farten er nul hvilket svarer til, at raketten vender og begynder at bevæge sig nedad.
D er det punkt, hvor raketten har nået sin slutfart som følge af luftmodstanden. Uden denne så var kurven en ret linje fra B til E.
E er sammenstødet med jorden. Farten går hurtigt til nul.
-
De er lige store, fordi det første areal er længden af vejen op og det sidste er længden af vejen ned. Da den bevæger sig lodret begge veje, så er dette samme strækning.
-
Arealet svarer til strækningen op og ned. Stigningen er halvdelen af 39.000 m = 19,5 km.
Dvs. raketten når op i en højde af 19,5 km
En satellit kredser om jorden med en fart af 7,80 km/s.
-
Hvad er satellittens højde over jorden?
Svar på opgave 12:
-
Satellitten antages at befinde sig en en jævn cirkelbevægelse om jordens massemidtpunkt. Den resulterende kraft på satellitten er centripetalkraften, som er lig med tyngdekraften. Der ses bort fra luftmodstand.
For centripetalkraften, FC, på satellitten i den jævne cirkelbevægelse gælder:
|FC| = m·v2/r, hvor
m er satellittens masse (går ud),
v er satellittens fart, som er opgivet til: 7,80 km/s = 7,80·103 m/s og
r er afstanden mellem satellittens massemidtpunkt og jordens massemidtpunkt.
For tyngdekraften, FT, på satellitten gælder:
|FT| = G·M·m/r2, hvor
G er gravitationskonstanten, som slås op til: 6,674·10-11 N·m2·kg-2 og
M er Jordens masse, som slås op til: 5,976·1024 kg
|FC| = |FT| ⇒ m·v2/r = G·M·m/r2 ⇒ r = v-2·G·M ⇒
r = (7,80·103 m/s)-2·(6,674·10-11 N·m2·kg-2)·(5,976·1024 kg) = 6,56·106 m.
Fra dette skal man trække Jordens radius på 6,34·106 m for at finde satellittens højde over jorden:
6,56·106 m - 6,34·106 m = 2,2·105 m
En fjerbold skydes afsted indendørs, og man måler dens fart i lodret retning. Målingerne fremgår af nedenstående skema:
| Tid (s) | 0,2 | 0,5 | 1,0 | 1,6 | 2,2 |
| Lodret fart (m/s) | 7,8 | 2,5 | −1,9 | −3,9 | −4,7 |
-
Vurder begyndelsesfarten for fjerbolden i lodret retning.
-
Til hvilket tidspunkt når fjerbolden sit højeste punkt?
-
Hvad er fjerboldens lodrette acceleration i dette punkt?
Svar på opgave 13:
Der er tale om et skråt kast med luftmodstand.
-
Nedenstående løsning er lavet i Ti-Nspire. Man laver først en liste over tider og en liste over fart:
tid:={0.2,0.5,1.,1.6,2.2} ▸ {0.2,0.5,1.,1.6,2.2}
fart:={7.8,2.5,−1.9,−3.9,−4.7} ▸ {7.8,2.5,−1.9,−3.9,−4.7}
På grundlag af listerne laver man en tredjegradsregression:
CubicReg tid,fart,1: CopyVar stat.RegEqn,f1: stat.results ▸
[["Titel","Tredjegradsregression"]
["RegEqn","a*x3+b*x2+c*x+d"]
["a",−2.67437]
["b",14.089]
["c",−25.8145]
["d",12.3614]
["R²",0.999553]
["Resid","{...}"]]Nedenfor er funktionens graf tegnet ind sammen med målepunkterne i Ti-Nspire.
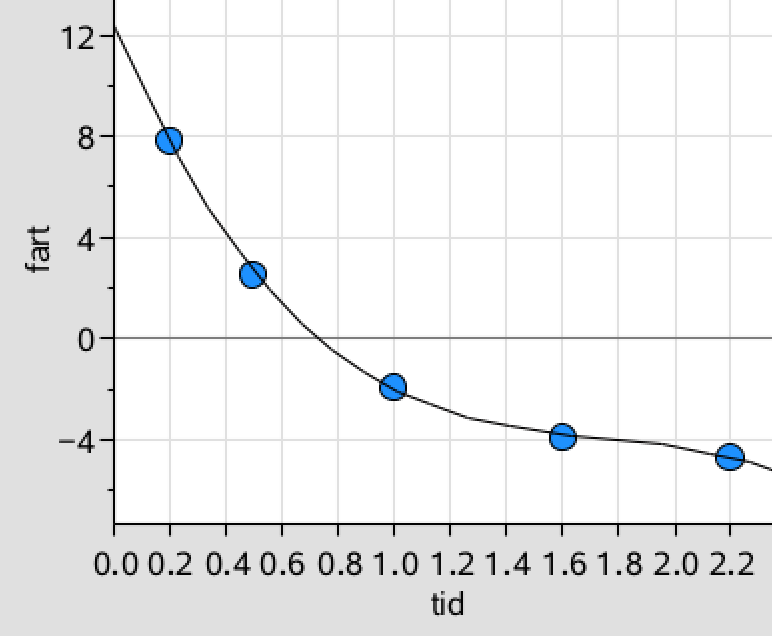
Det bemærkes, at regressionsfunktionen kun dur som tilnærmelse for 0,2 < x < 2,2 s. Her er x tiden i sekunder.
I Ti-Nspire oprettes regressionsfunktionen automatisk som f1(x).
Begyndelsesfarten kan tilnærmelsesvis findes som f1(0): f1(0) ▸ 12.36
Dvs. fjerboldens begyndelsesfart i lodret retning vurderes til 12 m/s
Den rigtige værdi er nok højere, da luftmodstanden er størst i starten, hvor farten også er størst. Dette betyder, at den rigtige kurve for fartens forløb formodentlig starter højere oppe og aftager hurtigere end tilnærmelsen mellem 0 og 0,2 s.
-
I det højerste punkt er den lodrette fart lig med 0, og man skal derfor løse ligningen f1(x) = 0:
solve(f1(x)=0,x) ▸ x=0.73
Dvs. det højeste punkt nås til tiden 0,73 s
-
Den lodrette acceleration i toppunktet er f1'(0,73), den afledte af fart-funktionen til det tidspunkt, hvor fjerbolden når sit højeste punkt.
derivative(f1(x),x)|x=0.73 ▸ −9.55
Dvs. den lodrette acceleration i toppunktet er 9,6 m/s2
PS: Dette passer med at den lodrette acceleration teoretisk set er lig med tyngdeaccelerationen, da fjerbolden kun påvirkes af tyngdekraften i lodret retning i dette punkt. Der er ingen luftmodstand i lodret retning i toppunktet, da der ikke er noget lodret fart.
En elektrisk jævnstrømskreds med polspændingen 4,0 V indeholder foruden en beskyttelses-modstand kaldet R1 også en trykfølsom modstand kaldet R2. Kredsen er vist nedenfor:
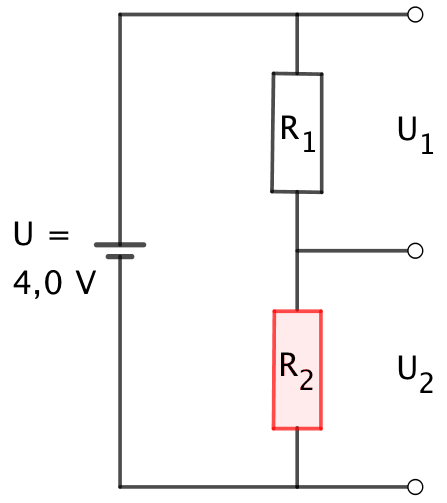
For den trykfølsomme modstand R2 gælder en sammenhæng mellem resistans og tryk (F), der er vist ved nedenstående diagram:
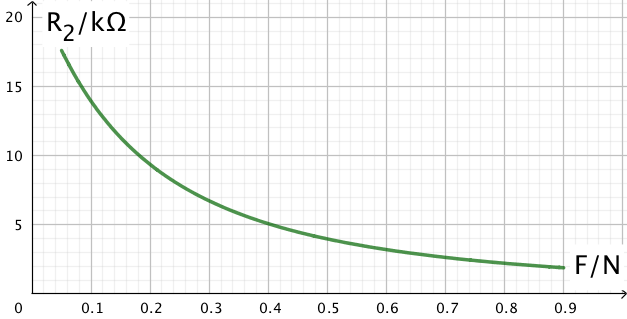
Man ønsker, at spændingen U2 skal være under 2,4 V, når trykket på modstanden er over 0,3 N.
-
Hvad skal modstanden R1 mindst være for, at dette krav er opfyldt?
Svar på opgave 14:
-
Man skal finde ud af hvad R1 er, når trykket på R2 er 0,3 N og vurdere om denne værdi af R1 er stor nok til at opfylde betingelsen for U2.
Man aflæser R2 til 6,7 kΩ ved trykket 0,3 N som vist nedenfor:
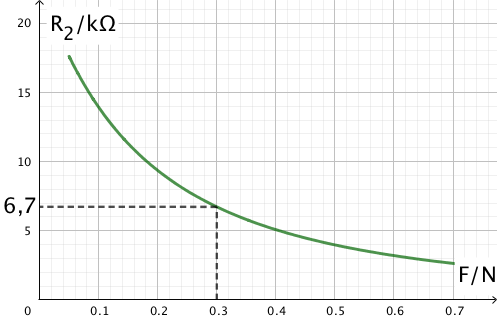
Da R1 og R2 er serieforbundet gælder, at U = U1 + U2 og R1/R2 = U1/U2 ⇒ R1 = ((U - U2)/U2)·R2 ⇒
R1 = ((4,0 V - 2,5 V)/(2,5 V))·(6,7 kΩ) = 4,0 kΩ.
U = U1 + U2 og U1/U2 = R1/R2 giver: U2 = U/(1 + R1/R2).
Af kurven ses, at R2 aftager med stigende tryk, og at nævneren i brøken U/(1 + R1/R2) dermed stiger med trykket. Dette betyder, at hele brøken og dermed også U2 aftager med voksende tryk.
Derfor er R1 = 4,0 kΩ den mindste modstand, der sikrer at U2 < 2,5 V, når F > 0,3 N.
Et ringformet kammer er omviklet med en elektrisk ledende spole, der har 150 vindinger. Gennem spolen går jævnstrøm på 2,13·105 A. En storcirkel, der går midt gennem kammeret hele vejen rundt, har radius 0,70 m.
-
Hvad er magnetfeltets styrke i kammeret?
Svar på opgave 15:
-
For magnetfeltets styrke, B, gælder i en ringformet spole:
B = I·μ0·N/(2·π·R), hvor
I er strømstyrken i spolen = 2,13·105 A,
R er storradius af ringen = 0,70 m,
μ0 er vakuumpermabiliteten, som slås op til 1,257·10-6 T·m/A og
N er antal vindinger = 150.
Dvs. magnetfeltets styrke er (2,13·105 A)·(1,257·10-6 T·m/A)·150/(2·π·(0,70 m)) = 9,13 T
En ion med ladningen 1,602·10-19 C og massen 1,153·10-26 kg bevæger sig vinkelret på et uniformt magnetfelt med styrken 0,518 T. Ionens fart er 3,78·106 m/s.
-
Hvad er kraften på ionen?
-
Hvad er radius i banen?
Ionen bevæger sig i en cirkulær bane i magnetfeltet.
Svar på opgave 16:
-
For kraften, FM, på en ion, der bevæger sig vinkelret på et uniformt magnetfelt, gælder:
FM = q·B·v, hvor
q er ionens ladning = 1,602·10-19 C,
B er magnetfeltets styrke = 0,518 T = 0,518 kg/(C·s) og
v er ionens fart = 3,78·106 m/s.
Dvs. kraften på ionen er (1,602·10-19 C)·(0,518 kg/(C·s))·(3,78·106 m/s) = 3,14·10-13 N
-
Den magnetiske kraft, som ionen udsættes for, er den resulterende kraft i en jævn cirkelbevægelse og dermed lig med centripetalkraften (FC) på ionen.
FM = FC ⇒ q·B·v = m·v2/R ⇒
R = m·v/(B·q), hvor
R er radius for cirkelbevægelsen og
m er ionens masse = 1,153·10-26 kg.
Dvs. radius i ionens bane er (1,153·10-26 kg)·(3,78·106 m/s)/[(0,518 kg/(C·s))·(1,602·10-19 C)] = 0,53 m
I et reaktionskammer med volumenet 49 m3 fastholdes plasma med to slags partikler i et magnetfelt ved temperaturen 1,80·108 K.
-
Hvad er den gennemsnitlige kinetiske energi for partiklerne i kammeret?
-
Hvad er reaktiviteten for fusionen i kammeret?
Der er lige mange af hver slags partikel og den samlede tæthed for partiklerne er 4,38·1019 pr. m3. Ved sammenstød mellem en partikler af hver slags kan der ske fusion. Energiproduktionen ved fusion mellem to partikler er 2,82·10-12 J. Gennemsnitseffekten for den samlede fusionsreaktion i kammeret er 1,57·107 W.
Svar på opgave 17:
-
Den gennemsnitlige kinetisk energi i plasma er Ekin = (3/2)·k·T, hvor
k er Boltzmanns konstant = 1,381·10-23 J/K og
T er den absolutte temperatur = 1,80·108 K
Den gennemsnitlige kinetiske energi i plasmaet er: (3/2)·(1,381·10-23 J/K)·(1,80·108 K) = 3,73·10-15 J
-
For fusion mellem to forskellige slags kerner, der optræder med lige stor tæthed, gælder:
σ·v12 = 4·P·n-2·V-1·Q-1 hvor
σ·v12 reaktiviteten,
P er gennemsnitseffekten ved fusionen for alle kerner, der reagerer = 1,57·107 W = 1,57·107 J/s,
Q er energiproduktionen i fusionen mellem to partikler = 17,6 MeV = 17,6·(1 MeV) = 17,6·1,602·10-13 J = 2,82·10-12 J,
n er tætheden af partikler = 4,38·1019 m-3 og
V er volumen af reaktor = 49 m3.
Man får: σ·v12 = 4·(1,57·107 J/s)·(4,38·1019 m-3)-2·(49 m3)-1·(2,82·10-12 J)-1 = 2,369·10-22 m3/s
Dvs. reaktiviteten i plasmaet er 2,37·10-22 m3/s