
Svar på opgave 1: Gallium
-
Rumfanget af gallium er massen divideret med densiteten = (25,5 g)/(5,9 g·cm-3) = 4,32 cm3
-
Der gælder, at varmen, der tilføres galliumfiguren er: Q = Qo + Qs, hvor
Qo er varmen, der går til opvarmning af fast gallium (figuren) til smeltepunktet og
Qs er varmen, der går til smeltning.
Qo = m·C·∆T, hvor
m = massen af gallium = 25,5 g,
C = den specifikke varmekapacitet for fast gallium = 373·103 J·g-1·K-1,
∆T = temperaturforskel for gallium fra start til smeltepunkt = (29,8 - 20,5) K = 9,3 K.
Qs = m·L, hvor
L = specifik smeltevarme for gallium = 80,2 kJ/kg = 80,2 J/g.
Dette giver:
Qo = m·C·∆T = (25,5 g)·(373·103 J·g-1·K-1)·(9,3 K) = 88,5 J
Qs = m·L = (25,5 g)·(80,2 J/g) = 2045 J
Tallene indsættes og man går den samlede varmemængde for opvarmning og smeltning af figuren:
Q = Qo + Qs = 88,5 J + 2045 J = 2,13·103 J
Fællestemperatur:
Der gælder, at QGa = Qv, hvor QGa er den varme som gallium modtager og Qv er den varme, som vandet afgiver. Slut- eller fællestemperaturen kaldes T. Man ved at T er større end begyndelsestemperaturen for gallium, da gallium modtager varme. Det modsatte gælder for vand. Der ses bort fra varmetab til omgivelserne. Man får:
QGa = 2,13·103 J + m·CGa(l)·(T - TGa(l)), hvor
2,13·103 J er energien til opvarming og smeltning af fast gallium (galliumfiguren),
CGa(l) er den specifikke varmekapacitet for flydende gallium = 0,414 J/(g·K) og
TGa(l) er er starttemperaturen for flydende gallium = smeltepunktet for gallium = 29,8 °C. Denne temperatur er mindre end T, så ved at trække den fra T, så får man en positiv Q-værdi.
Qv = mv·Cv·(Tv - T), hvor
mv er massen af vand = 96,7 g,
Cv er vands specifikke varmekapacitet = 4,18 J/(g·K) og
Tv er starttemperaturen for vand = 51,2 °C. Denne temperatur er større end T, så ved at trække T fra den, så får man en positiv Q-værdi.
Man indsætter tallene med enheder (enheden K erstattes med °C, der har samme størrelse. At de to enheder har forskellige nulpunkter spiller ikke nogen rolle, når man ser på forskelle i temperatur.):
QGa = 2134 J + (25,5 g)·(0,414 J/(°C·g))·(T - 29,8 °C) = 2,13·103 J + (10,56 J/°C)·(T - 29,8 °C)
Qv = (96,7 g)·(4,18 J/(°C·g))·(51,2 °C - T) = (404,2 J/°C)·(51,2 °C - T)
Man løser ligningen QGa = Qv med hensyn til T:
2,13·103 J + (10,56 J/°C)·(T - 29,8 °C) = (404,2 J/°C)·(51,2 °C - T) ⇒ T = 45,5 °C.
Dvs. fællestemperaturen for gallium og vand er 45,5 °C

Svar på opgave 2: Udvidelse af blodåre
-
P-32 henfalder ved beta-minus henfald. Reaktionsskemaet er vist nedenunder. Der dannes S-32, en elektron og en antineutrino.

Nukleontal (de øverste tal i reaktionskemaet) stemmer og det samme gør ladninger (de nederste tal). Leptontallet stemmer, idet elektronen har leptontallet 1 og antineutrinoen har leptontallet -1.
-
Antallet af henfald i løbet af de første 30 døgn er aktiviteten af P-32 integreret fra t = 0 til t = 30 døgn.
Formlen for aktiviteten er: A = A0·(½)(t/T½), hvor
A0 er startaktiviteten = 370 kBq,
t er tiden og
T½ er halveringstiden for henfald af P-32 = 14,28 døgn.
Man regner aktiviteten om til henfald pr. døgn: (370·103 s-1)·(24·3600 s/døgn) = 3,197·1010 døgn-1
Man får følgende i Ti-Nspire:
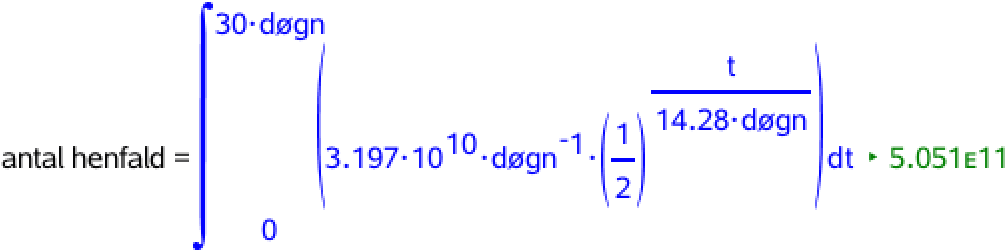
Energien er antallet af henfald gange energien pr. henfald: 5,05·1011·8,2·10-14 J = 4,1·10-2 J.
Dvs. der afsættes 4,1·10-2 J i nærheden af trådnettet i de første 30 døgn.

Svar på opgave 3: Den elektriske racerbil TC-X
-
Gennemsnitsfarten er distance divideret med tid = (201,17 m)/(4,897 s) = 41,08 m/s
-
Der gælder følgende for lineær bevægelse med konstant acceleration og begyndelsesfarten 0:
Δs(t) = ½·a·t2 og v(t) = a·t hvor
Δs(t) er den tilbagelagte strækning til tiden t,
a er den konstante acceleration = 24,2 m·s-2,
v(t) er farten til tiden t.
Man sætter det tidspunkt, hvor slutfarten opnås, lig med t1. Der gælder: v(t1) = 100 km/h = 100·(103 m)/(3600 s) = 27,8 m/s. Dette indsættes i formlen for Δs(t1):
Δs(t1) = ½·a·(t1)2 ∧ v(t1) = a·t1 ⇒ Δs(t1) = (v(t1))2/(2a) = (27,8 m/s)2/(2·24,2 m/s2) = 15,9 m
Dvs. bilen når en fart af 100 km/h efter at have tilbagelagt 15,9 m
(PS: Man kan godt regne t1 ud, men det er ikke nødvendigt.)
-
Man opretter lister med tid og fart.
tid:={0.7,0.8,0.9,1.,1.1,1.2,1.3} ▸ {0.7,0.8,0.9,1.,1.1,1.2,1.3}
fart:={20.3,22.3,24.3,26.1,27.8,29.4,30.9} ▸ {20.3,22.3,24.3,26.1,27.8,29.4,30.9}
Man afbilder fart som funktion af tiden i et koordinatsystem:
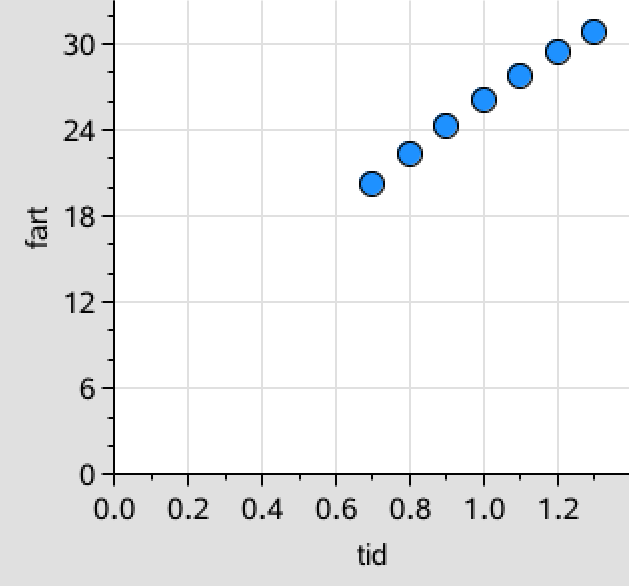
Kurven har en svag krumning, og man vælger derfor en potensregression som vist:
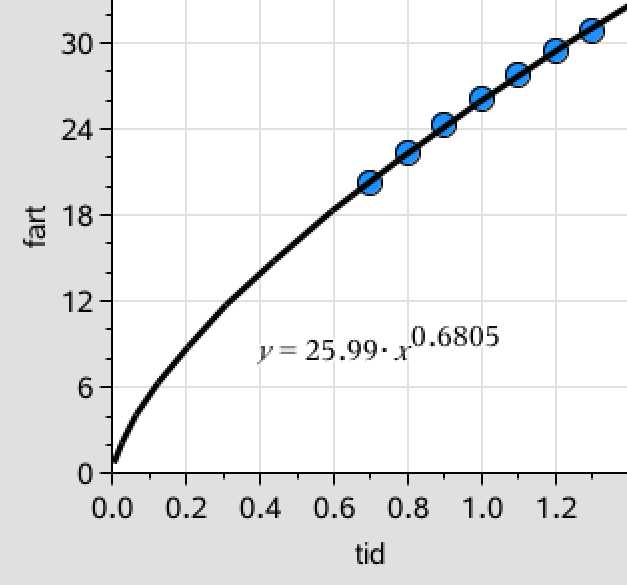
Man får følgende formel for farten: v(t) = 26·t0,68. (Der rundes af til to betydende cifre, idet tiden måles med en til to betydende cifre, mens farten måles med tre.)
Man differentierer dette udtryk med hensyn til t og får accelerationen:
a(t) = v'(t) = 0,68·26·t0,68-1 m·s-2 = 17,7·t-0,32 m·s-2.
Heraf findes accelerationen til 0,8 s:
a(0,8) = 17,7·0,8-0,32 m·s-2 = 19 m·s-2
Slutacceleration:
For kørsel med konstant effekt gælder: v(t) = k·t0,5. Tilsyneladende er meningen, at v(t) = 26·t0,68 til og med t = 0,8 s, mens v(t) = k·t0,5 gælder derefter. Det er derfor ikke meningen, at man skal bruge v(t) = 26·t0,68 og forsøge at regne sig frem til sluttidspunkt for derefter at differentiere v(t) og finde a(t) for dette tidspunkt.
Ved konstant motoreffekt, P, gælder: F·v = P ⇒ a·m·v = P ⇒ a·v = P/m, hvor
F er bilens motorkraft,
v er bilens fart,
a er bilens acceleration og
m er bilens masse.
Undervejs er brugt Newtons anden lov: F = m·a. Desuden skal a·v generelt opfattes som et skalarprodukt af vektorer, men da a og v har samme retning, så er skalarproduktet lig med produktet af a og v's numeriske værdier.
Da P/m er en konstant, så gælder, at a0,8·v0,8 = as·vs, hvor
a0,8 er accelerationen til tiden 0,8 s = 19 m·s-2,
v0,8 er farten til tiden 0,8 s = 26·0,80,68 m·s-1 = 22,3 m·s-1,
as er accelerationen til sluttidspunktet og
vs er farten til sluttidspunktet = 64,7 m·s-1.
Dette giver: as = a0,8·v0,8/vs = (19 m·s-2)·(22,3 m·s-1)/(64,7 m·s-1) = 6,55 m·s-2
Dvs. bilens slutacceleration er 6,6 m·s-2

Svar på opgave 4: Pladespiller
-
Frekvensen af spændingen er antal perioder pr. tidsenhed. Det ses af figuren, at der mellem 0,0006 s og 0,0073 s er 3 perioder.
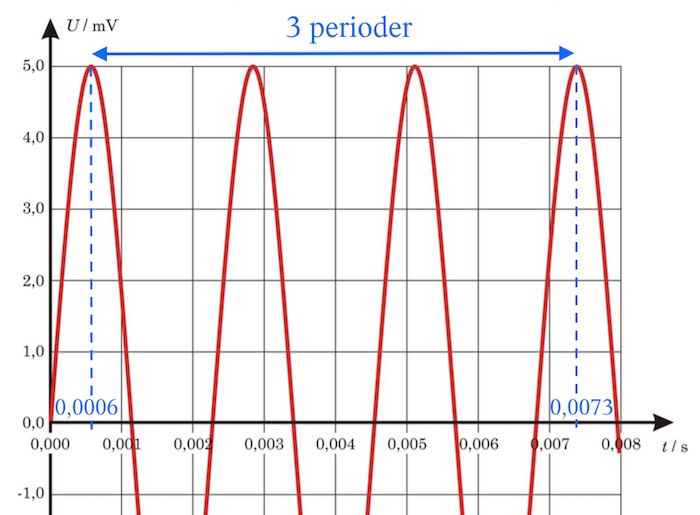
Dette giver frekvensen: 3/(0,0073 s - 0,0006 s) = 448 Hz
-
Et ydre magnetfelt, der ændres med tiden, vil inducere en spænding i en ringformet leder. Når de magnetiske feltlinjer er vinkelrette på den cirkel, som lederen afgrænser, så er denne spænding (U) er lig med ændring i magnetisk flux pr. tidsenhed (dΦB/dt) gange antal vindinger (N) i lederen. Dette giver følgende differentialligning:
U = -N·(dΦB/dt) og ΦB(0) = 0. Denne løses med hensyn til den magnetiske flux:
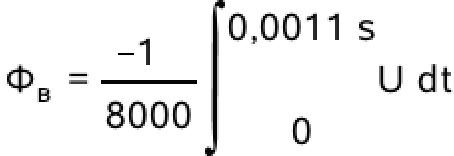
Minustegnet betyder, at det inducerede magnetfelt modvirker det ydre (Lenz's lov).
Integralet kan findes som arealet under kurven fra t = 0 til t = 0,0011 s. Nedenunder er arealet under denne del af kurven målt i Geogebra til 3,64 enheder (brunt område). Den blå ramme vist på figuren er målt til 40,9 enheder. Den blå ramme har et areal på (5,0·10-3 V)·(8,0·10-3 s) = 4,0·10-5 Wb.
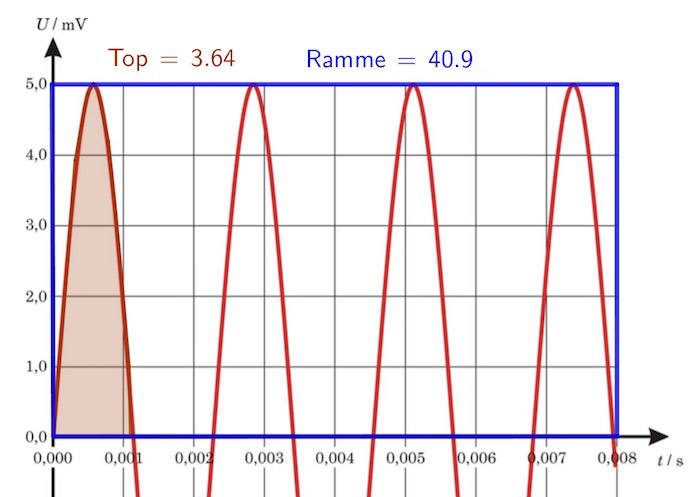
Arealet under kurven svarer dermed til (3,64/40,9)·(4,0·10-5 Wb) = 3,6·10-6 Wb.
Dvs. den numeriske værdi af fluxen fra t = 0 til t = 0,0011 s er (3,6·10-6 Wb)/8000 = 4,5·10-10 Wb

Svar på opgave 5: Cassini på tur i Solsystemet
-
Kraften (F) beregnes ved hjælp af tyngdekraftformlen: F = G·M·m/r2, hvor
G er gravitationskonstanten = 6,674·10-11 N·m2·kg-2
M er Jordens masse = 5,976·1024 kg,
m er Cassinis masse = 5,257·103 kg og
r er afstanden mellem centrum af Jordens centrum og Cassinis massemidtpunkt = 7,568·106 m.
Med værdierne indsat får man følgende kraft mellem Jorden og Cassini:
F = (6,674·10-11 N·m2·kg-2)·(5,976·1024 kg)·(5,257·103 kg)/(7,568·106 m)2 = 3,66·104 N
-
Man antager, at der gælder mekanisk energibevarelse, dvs. ΔEkin + ΔEpot = 0, hvor
ΔEkin er den kinetiske energi for Cassini og
ΔEpot er den potentielle energi for Cassini.
ΔEkin = ½·m·[(v2)2 - (v1)2], hvor
v1 er Cassinis fart i afstanden 2,0056·108 m fra Venus = 6293 m·s-1 og
v2 er Cassinis fart ved nærmeste afstand = 1,1785·104 m·s-1
ΔEpot = -G·M·m·(1/r2 - 1/r1), hvor
r1 er start-afstanden mellem Jorden og Cassini 2,0056·108 m og
r2 er den nærmeste afstand mellem Cassinis massemidtpunkt og Jordens centrum.
Man får: ΔEkin = -ΔEpot ⇒
½·[(v2)2 - (v1)2] = G·M·(1/r2 - 1/r1) ⇒
½·[(1,1785·104 m·s-1)2 - (6,293·103 m·s-1)2] = (6,674·10-11·s-2 m3)·(4,8675·1024)·(1/r2 - 1/(2,0056·108 m)) ⇒
4,964·107 m2·s-2 = (3,2486·1014 m3·s-2)·(1/r2 - (4,986·10-9 m-1)) ⇒
r2 = 6,337·106 m
Afstanden fra Cassini til Venus' overflade er denne afstand minus Venus' radius (Venus forudsættes at være kugleformet): 6,337·106 m - 6,052·106 m = 2,854·105 m.
Dvs. afstanden fra Cassini til Venus' overflade er 2,854·105 m
-
For at finde ændringen i Cassinis kinetiske energi (ΔEkin) ved forbiflyvningen af Jorden, så skal man kende ændringen i længden af Cassinis hastighedsvektor.
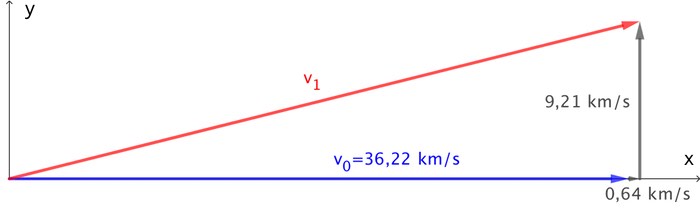
I starten har Cassini hastighedsvektoren v0 = (36,22 km/s;0) i xy-koordinatsystemet. Dernæst får den lagt 0,64 km/s i x-aksens retning og 9,21 km/s i y-aksens. Dvs. den nye hastighedsvektor bliver v1 = (36,86 km/s; 9,21 km/s).
Den første hastighedsvektor har længden v0 = 36,22 km/s. Længden af den anden findes ved hjælp af Pythagoras læresætning: v1 = √[(36,86 km/s)2 + (9,21 km/s)2] = 37,99 km/s.
ΔEkin = ½·m·[(v1)2 - (v0)2] = ½·(5257 kg)·((37,99·103 m/s)2 - (36,22·103 m/s)2) =
3,452·1011 kg·m2·s-2.
Dvs. ændringen i Cassinis kinetisk energi ved forbiflyvningen af Jorden er 3,45·1011 J

Svar på opgave 6: Tokamakken JT-60
-
Den gennemsnitlige kinetisk energi i plasma er Ekin = (3/2)·k·T, hvor
k er Boltzmanns konstant = 1,381·10-23 J/K og
T er den absolutte temperatur = 190·106 K
Man får: Ekin = (3/2)·(1,381·10-23 J/K)·(190·106 K) = 3,94·10-15 J
-
For fusion mellem to slags kerner, der optræder med lige stor tæthed, gælder: P = Q·¼·n2·σ·v12·V ⇒
n = √[4·P/(Q·σ·v12·V)], hvor
P er gennemsnitseffekten ved fusionen for alle kerner, der reagerer,
Q er energiproduktionen i fusionen mellem en deuteriumkerne og en tritiumkerne
= 17,6 MeV = 17,6·1,602·10-13 J = 2,82·10-12 J,n er tætheden af kerner,
σ·v12 reaktiviteten (aflæses) og
V er volumen af reaktor = 54 m3.
Af grafen nedenunder aflæses σ·v12 til 4,1·10-22 m3/s som vist:
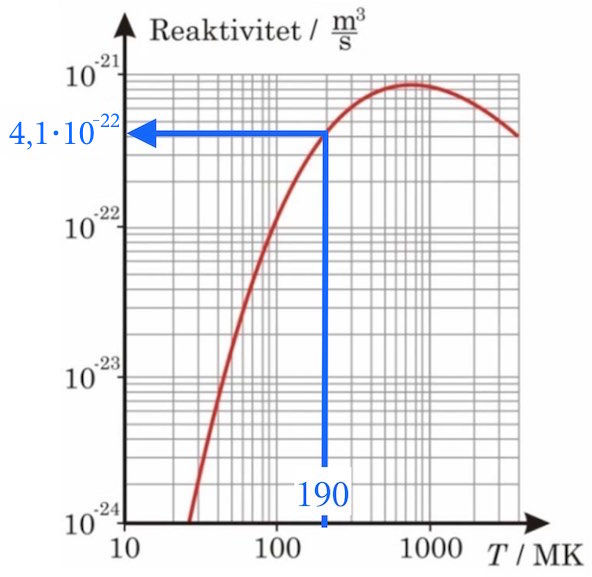
Man får: n = √[4·12,5·106 J·s-1/(2,82·10-12 J)·(4,1·10-22 m3·s-1)·(54 m3)] = 2,83·1019 m-3
Dvs. der er 2,8·1019 kerner i reaktoren pr. kubikmeter

Svar på opgave 7: Kanalrundfart for turister
-
Båden antages at være 15 m lang og 5 m bred. Det antages, at der 70 turister a 70 kg ombord, dvs. at turisterne vejer ca. 5 t.
Det antages, at båden er kasseformet, så ændringen i dens dybgang er proportional med mindskelsen af dens masse.
Der gælder: Δh·ρ·A = Δm ⇒ Δh = Δm/(ρ·A), hvor
Δh er forskellen i dybgang,
A er tværsnitarealet vandret gennem båden ved vandlinjen = (5 m)·(15 m) = 75 m2,
ρ er havvandets densitet = 1,0 ton·m-3
Δm er ændringen i masse, når turisterne forlader båden = 5 tons.
Man får følgende hævning af båden: Δh = ρ·Δm/A = (5 ton)/[(1,0 ton·m-3)·(75 m2)] = 0,07 m
Dvs. båden hæver sig 7 cm, når turisterne stiger ud.