
Svar på opgave 1: Optøning af vandrør
-
Effekten (P) er lig med spændingsfald (U) gange strømstyrke (I), eller: P = U·I. Man får:
425 W = (1,13 V)·I ⇒ I = (425 W)/(1,13 V) = 376 A
-
Man skal opvarme jernrør og is fra -15 °C til 0°C. Dernæst skal isen tøes op.
Man skal kende den specifikke varmefylde for jern (cjern) og is (cis), tillige med is' specifikke smeltevarme (Lis) og temperaturændringen (ΔT). Man slår følgende op:
cjern = 449 J/(kg·K)
cis = 2040 J/(kg·K)
Lis = 334 kJ/kg = 334000 J/kg
ΔT = Tslut - Tstart = 0 °C - (-15 °C) = 15 °C.
Man har, at effekt er lig med energitilførsel (ΔE) pr. tidsenhed eller P = ΔE/Δt. Her skal man finde Δt: P = ΔE/Δt ⇔ Δt = ΔE/P. For at finde ΔE deles den op i to: energien for opvamning (ΔEopv) og energien for smeltning (ΔEsme). Man får:
ΔE = ΔEopv + ΔEsme = (cjern·mjern + cis·mis)·ΔT + Lis·mis =
([449 J/(kg·K)]·9,48 kg + [2040 J/(kg·K)]·2,04 kg)·(15°C) + (334000 J/kg)·2,04 kg = 807632 J
Dvs. den tid, som skal bruges på opvamning er:
Δt = ΔE/P = (807632 J)/(425 W) = (807632 J)/(425 J/s) = 807632/425 s = 1900 s = 1900·(1/60) min. = 31,7 min.

Svar på opgave 2: Galaksen EGS-zs8-1
-
Der gælder, at f = c/λ, hvor c er lysets hastighed, λ er spektrallinjens bølgelængde og f er spektrallinjens frekvens, som skal findes.
c = 3,00·108 m/s.
λ = 1061,6 nm = 1061,6·10-9 m = 1,0616·10-6 m (infrarødt lys).
Man får: f = (3,00·108 m/s)/(1,0616·10-6 m) = 2,8239·108+6 s-1 = 2,82·1014 s-1
-
Rødforskydningen z er defineret som:
z = (λmodtaget - λudsendt)/λudsendt.
Dvs. rødforskydningen er (1061,6 nm - 121,6 nm)/(121,6 nm) = 7,73

Svar på opgave 3: Forurening med iod
-
I følge tabelopslag følger isotopen iod-134 et beta-henfald:
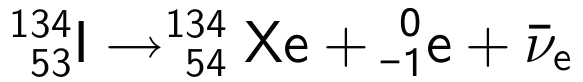
hvor der dannes Xenon-134, en elektron og en antineutrino. Der gælder bevarelse af nukleontal (134), ladning af protoner og elektroner (53) og leptontal (0). Elektronen har leptontallet 1 og antineutrino har -1.
-
Det antages, at det radioaktive Iod-131 i bugten ikke fortyndes af havvand uden for bugten.
Aktiviteten (A) som funktion af tiden (t) er givet ved A = A0·(1/2)t/T1/2, hvor
A0 er startaktiviteten = 20·103 Bq/L og T1/2 er halveringstiden for Iod-131.
Halveringstiden for Iod-131 slås op til 8,02 døgn.
Man skal løse ligningen 10 Bq/L = (20·103 Bq/L)·0,5t/(8,02 døgn) med hensyn til t:
solve(10*(bq/l)=20*103*(bq/l)*0.5t/(8.02*døgn),t) ▸ t=87.9456*døgn
Dvs. det tager 88 døgn før aktiviteten af Iod-131 i bugtens havvand er kommet under den tilladte værdi.
-
Ved tabelopslag finder man, at der pr. henfald for Iod-131 afgives en elektron med en maksimal energi på 0,61 MeV og et gammakvant med en maksimal energi på 0,364 MeV.
Den samlede strålingsenergi pr. henfald er derfor:
0,61 MeV + 0,364 MeV = 0,974 MeV =
(0,974·106 eV)·(1,6022·10-19 J/eV) = 0,974·1,6022·106-19 J = 1,56054·10-13 J
Strålingseffekten (P) er lig med aktivitet gange strålingsenergi, dvs:
P = [(1,0 L)·(20·103 Bq/L)]·(1,5605·10-13 J) = 3,1211·10-9 Bq·J = 3,1211·10-9 s-1·J = 3,1·10-9 W

Svar på opgave 4: Squashbold i vand
-
Opdriften (F) på squashbolden er lig med tyngden af det vand, som den fortrænger.
Tyngden af fortrængt vand er lig med rumfanget af bolden gange massefylden af vand gange tyngdeaccelerationen eller
F = (4/3)·π·(rbold)3·ρvand·g =
(4/3)·π·(20,2 mm)3·[1,0 kg/dm3]·9,82 m/s2 =
(4/3)·π·(20,2·10-3 m)3·[1,0 kg/(10-1 m)3]·9,82 m/s2 =
(4/3)·π·20,23·10-9 m3·1,0 kg·103 m-3·9,82 m/s2 =
(4/3)·π·20,23·1,0·9,82·10-9+3 m3-3+1·kg/s2 =
339043·10-6 N = 0,34 N
-
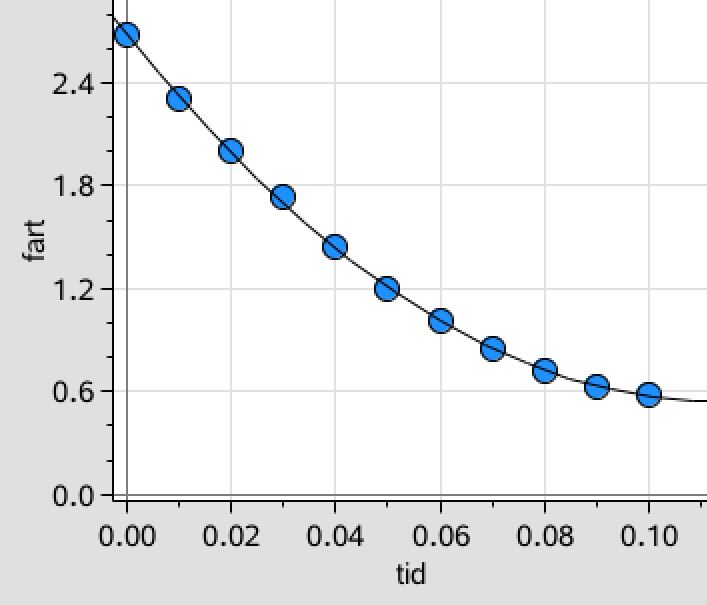
Man opretter lister med tid og fart i Ti-Nspire:
tid:={0,0.01,0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.09,0.1} ▸ {0,0.01,0.02,0.03,0.04,0.05,0.06,0.07,0.08,0.09,0.1}
fart:={2.68,2.31,2.,1.73,1.44,1.2,1.01,0.85,0.72,0.63,0.58} ▸ {2.68,2.31,2.,1.73,1.44,1.2,1.01,0.85,0.72,0.63,0.58}
Man plotter fart som funktion af tid. Punkternes forløb ser ud til at kunne tilnærmes med et andengradspolynomium. Man laver en polynomie-regression med graden 2 på listerne:

Nedenfor er polynomiet tegnet ind i et plot af fart som funktion af tiden. Der ser ud til at være god overensstemmelse mellem punkterne og polynomiet i det undersøgte interval af tiden.

Figuren til højre viser de kræfter, der virker på bolden:
Her er Ft lig med tyngdekraften, der virker nedad, mens Fo er opdriften virker opad. Fg gnidningskraften, virker modsat bevægelsesretningen og dermed også opad.
Den resulterende kraft på bolden (Fr) er givet ved: Fr = Ft - Fo - Fg.
Fg afhænger af farten og dermed tiden. Efter ca. 0,11 sek. - at dømme efter kurven - er accelerationen på bolden 0. Herefter bevæger den sig nedad i en ret linje med konstant fart, og som følge heraf må den resulterende kraft på bolden være 0 (Newtons 1. lov).
Efter tiden 0,07 s ændrer bolden stadig fart og dermed er den resulterende kraft på bolden forskellig fra 0.
Denne resulterende kraft er lig med massen af bolden gange med dens acceleration, som findes ud fra det tilnærmede polynomium til farten, der er P(t) = 166,55·t2 - 37,7914·t + 2,68392 m/s.
Accelerationen til t = 0,07 s er P'(0,07) = 2·166,55·(0,07) - 37,791 m/s2 = −14,5 m/s2.
Boldens masse er 22,4 g = 0,0224 kg. Opdriften (Fo) efter 0,07 s kendes som 0,34 N fra forrige spørgsmål. Dermed har man følgende ligning til at finde Fg efter 0,07 s:
Fg = Ft - Fo - Fr ⇒ Fg = m·g - 0,34 N - m·a ⇒
Fg = 0,0224 kg·9,82 m/s2 - 0,34 N - 0,0224 kg·(−14,5 m/s2) =
0,0224 kg·9,82 m/s2 - 0,34 N - 0,0224 kg·(−14,5 m/s2) = 0,20 N
Som før nævnt er gnidningskraften rettet opad, når bevægelsen foregår nedad.

Svar på opgave 5: Hockey
-
Boldens kinetiske energi er 0,5·m·v2 =
0,5·(0,160 kg)·(39 m/s)2 = 121,68 kg·m2·s-2 = 122 J
-
Der gælder impulsbevarelse eller bevægelsesmængde-bevarelse ved sammenstødet mellem stav og bold. Dette kan skrives:
F·Δt = m·v, hvor
F er den gennemsnitlige kraft på bolden fra staven,
Δt er den tid, som sammenstødet mellem bold og stav tager,
m er massen af bold og
v er boldens fart lige efter sammenstødet.
Man skal finde F og får:
F = m·v/Δt = (0,160 kg)·(39 m/s)/(97 ms) =
0,160·39/97 (kg·m/s)/(10-3 s) =
(0,160·39/97)·103 kg·m/s2 =
64 N
-
Der antages at være tale om et skråt kast uden luftmodstand. For den vandrette strækning, som bolden bevæger sig (eller kastelængden), gælder
Vandret strækning = (v0)2·sin(2·α)/g. Her er
v0 boldens fart i udgangspunktet,
α er vinklen mellem vandret og boldens bevægelsesretning i udgangspunktet og
g er tyngdeaccelerationen.
Her skal man finde α og det gøres ved formlen for stighøjden (ymax), som man kender. Formlen er:
ymax = (v0)2·sin2(α)/(2·g) ⇒
0,40 m = (39 m/s)2·sin2(α)/(2·9,82 m/s2) ⇒
sin2(α) = [(0,40 m)/(39 m/s)2]·(2·9,82 m/s2) = 0,005165 ⇒
sin(α) = √0,005165 = 0,071868 ⇒
α = sin-1(0,071868) = 4,121°
Dette α indsættes i formlen for boldens vandrette strækning, som giver:
(39 m/s)2·sin(2·4,121°)/(9,82 m/s2) = 22 m

Svar på opgave 6: Trappeløb
-
Det antages at der sker et varmetab i kroppen, dvs. kroppens effekt (P) både går til arbejde og varme. Kroppens nyttevirkning (η) sættes til 0,3, dvs 30 % af kroppens energi går til arbejde og 70 % til varme.
Hvert skridt, som kvinden tager, er i praksis et uelastisk sammenstød mellem hendes fod og trappen. Dette betyder et energitab. Når hun sætter af, vil der ske et yderligere energitab, idet hun glider en lille smule baglæns. Det bemærkes, at friktionen med underlaget er til fordel for hendes fremdrift: jo højere friktionen er, jo mindre tab af energi. I det følgende antages det, at dette energitab ikke har betydning. Man ser i øvrigt bort fra luftmodstand.
Kvindens arbejdseffekt (Parb) er det arbejde mod tyngdekraften (ΔA), som hun udfører, divideret med den tid, som det tager. Der gælder formlen:
Parb = ΔA/Δt = m·g·H/Δt, hvor
m er kvindens masse,
g er tyngdeaccelerationen og
H er trappens højde.
Tyngdeaccelerationen g = 9,82 m/s2. Det antages, at H = 10 m, m = 60 kg og Δt = 50 s. Man får:
Parb = (10 m)·(60 kg)·(9,82 m/s2)/(50 s) = 118 W
Kvindens samlede effekt er P = Parb/η = (118 W)/0,3 = 4,0·102 W

Svar på opgave 7: Tokamak
-
Man bruger formlen for den magnetiske fluxtæthed (B) i en torus og isolerer strømstyrken (I):
I = 2·π·B·r/(μ0·N), hvor
r er storradius af ringen,
μ0 er vakuumpermabiliteten (= 1,257·10-6 T·m/A) og
N er antal vindinger.
Man får I = 2·π·(5,3 T)·(0,67 m)/[(1,257·10-6 T·m/A)·120] = 1,48·105 A
-
Man bruger idealgasligningen for plasma:
p = n·kB·T, hvor
p er trykket i plasmaet,
n er antallet af partikler pr. kubikmeter,
kB er Boltzmanns konstant (= 1,381·10-23 J/K) og
T er lig med Kelvin-temperaturen.
Antallet af partikler og trykket findes af graferne ved 1,5 s. Trykket aflæses til 200 kPa. Antallet af elektroner aflæses til 3,4·1020 m-3.
Et deuterium-atom består af en kerne med een elektron, dvs. for hver elektron i deuterium-plasmaet er der en kerne, og det samlede antal partikler (kerne + elektroner) er derfor to gange antallet af elektroner.
Dermed er n i formlen lig med 2·3,4·1020 m-3 = 6,8·1020 m-3.
Man får temperaturen T = p/(n·kB) = (200·103 Pa)/[(6,8·1020 m-3)·(1,381·10-23 J/K)] =
200/(6,8·1,381)·1023-20+3 N·m-2·J-1·K·m3 = 21,2974·106 Nm·J-1·K = 2,1·107 K