Svar på opgave 1: Laserbehandling
-
Energien af en foton er givet ved formlen: Efoton = (ℏ·c)/λ,
hvor ℏ er Plancks konstant, c er lysets hastighed og lambda er lysets bølgelængde. Man indsætter:
ℏ = 6,63·10−34 J·s, λ = 532 nm og c = 3,00·108 m/s, og man får:
Efoton = (6,63·10−34 J·s)·(3,00·108 m/s)/(532·10-9 m) = [6,63·3,00/532]·10−34·108/10-9 (J·s·m/s)/m =
[6,63·3,00/532]·10−34+8+9 J = 3,74·10-19 J.
Dette kan omskrives til eV, idet 1 eV = 1,602·10-19 J. Man får: (3,74·10-19 J)/(1,602·10-19 J/eV) = (3,74/1,602) eV = 2,33 eV.
Dvs. fotonens energi er 2,33 eV
-
En effekt på 5,3 W betyder, at der på 1 sekund tilføres 5,3 J til vandet i huden. Denne energi skal bruges til at varme vandet op til kogepunktet og fordampe det ved 100 °C.
Den energi, der kræves, er givet ved formlen: ΔE = m·ΔT·cp + m·Lf,
hvor m er vandets masse, ΔT ændingen i temperatur under opvamning til kogepunkt, cp er vandets specifikke varmekapacitet og Lf er vandets fordampningsvarme.
Hudens temperatur er ca. 35 °C. Dvs. ΔT = (100 - 35) °C = 65 °C (eller 65 K).
Fra tabelopslag har man: cp = 4,18 J/(g·K) og Lf = 2250 kJ/kg.
Man får følgende ligning, som skal løses med hensyn til vandets masse m:
5,3 J = m·(65 K)·(4,18 J/(g·K)) + m·(2250 kJ/kg) ⇒ 5,3 J = m·(65·4,18 + 2250) J/g ⇒
m = [5,3/(65·4,18 + 2250)] g ⇒ m = 0,002102 g
Dvs. på et sekund fordamper 2,1 mg vand
Svar på opgave 2: Napoleons død
-
Ved tabelopslag finder man, at Arsen omdannes til Selen ved β- henfald under udsendelse af en antineutrino. Det skrives:
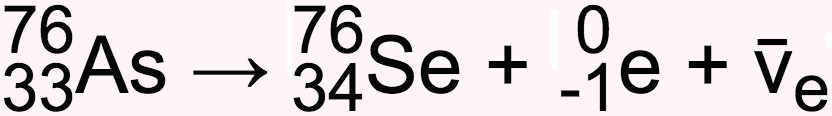
-
Massen af 76As-kerner er lig med antal kerner gange massen af en kerne. Massen af en kerne er i følge tabel 75,922 u = 75,922·1,66·10-27 kg = 1,260·10-25 kg = 1,260·10-22 g.
Der gælder følgende formel for aktiviteten af As: A = k·N. Her er A aktiviteten, k er aktivitetskonstanten og N er antallet af 76As-kerner.
Aktivitetskonstanten k findes som ln(2) divideret med halveringskonstanten. Ved tabelopslag findes halveringskonstanten for henfald af 76As til 26,3 timer. Dette giver, at k = ln(2)/(26,3 timer) = 0,6931/(26,3·3600 s) = 0,00000732 s-1
A = 46,5 Bq = 46,5 s-1. Dette giver følgende ligning for N, antallet af 76As-kerner:
46,5 s-1 = 0,00000732 s-1·N ⇒ N = 46,5/0,00000732 = 6,35·106
Dvs. massen af 76As-kerner er 6,35·106·1,260·10-22 g = 8,00·10−16 g, hvilket er mindre end 2,92·10-14 g
Svar på opgave 3: Kenguru
-
Der gælder Newtons anden lov: F = m·a ⇒ a = F/m, hvor F er kraften, m er massen af bil med passager og a er accelerationen af bil med passager.
F = 2,1 kN og m = 575 kg. Det giver følgende acceleration: a = (2100 N)/(575 kg) = 3,65 m/s2
-
For effekten gælder: P = ΔE/Δt, hvor P er effekten, E er energien og t er tiden.
Her er ΔE = 36 MJ og Δt = Δs/Δv = 95 km/(38 km/t).
Det giver effekten: P = 36 MJ/(95 km/(38 km/t)) = (36·106 J)/(95 km/(38 km/3600 s)) = [36·38/(95·3600)]·106 J/s = 4000 W = 4,0 kW
Svar på opgave 4: Copenhagen Suborbitals
-
Den kinetiske energi er givet ved formlen ΔEkin = (1/2)·m·v2, hvor Ekin er den kinetiske energi, m er rakettens masse, når den er tom og v er maksimalhastigheden.
ΔEkin = (1/2)·(144,6 kg)·(331 m/s)2 = 7,921·106 kg·m2/s2 = 7,92 MJ
-
Det bemærkes, at kurven viser rakettens hastighed, og at det antages, at raketten bevæger sig lodret op eller ned langs en ret linje. Stedfunktionen kan findes som arealet under kurven.
Man finder maksimumværdien af stedfunktionen s(t), der er givet som integralet af v(t) fra start indtil det tidspunkt, hvor den lodrette hastighed er lig med 0. Man bruger en graf af v(t) som funktion af tiden for at vurdere dette integrale.
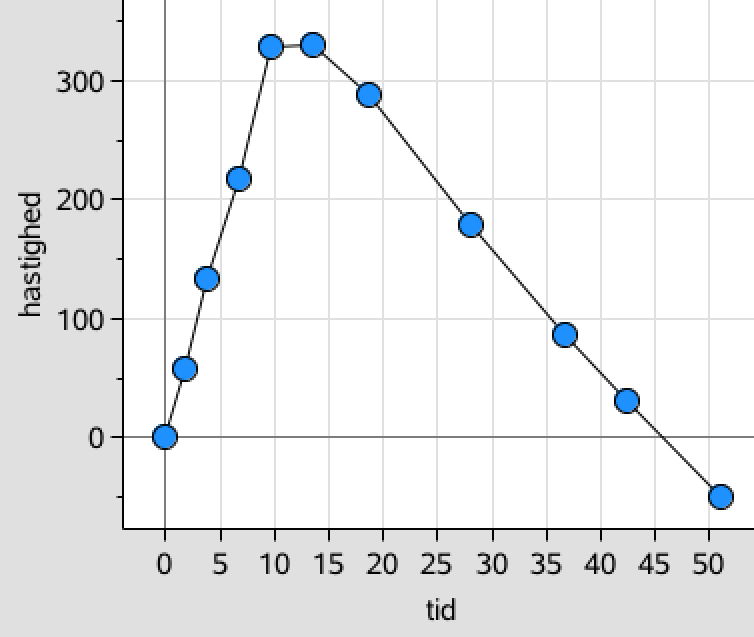
I dette tilfælde vurderes integralet eller arealet under kurven ved hjælp af en trekant ABC, der er vist med rødt nedenunder.
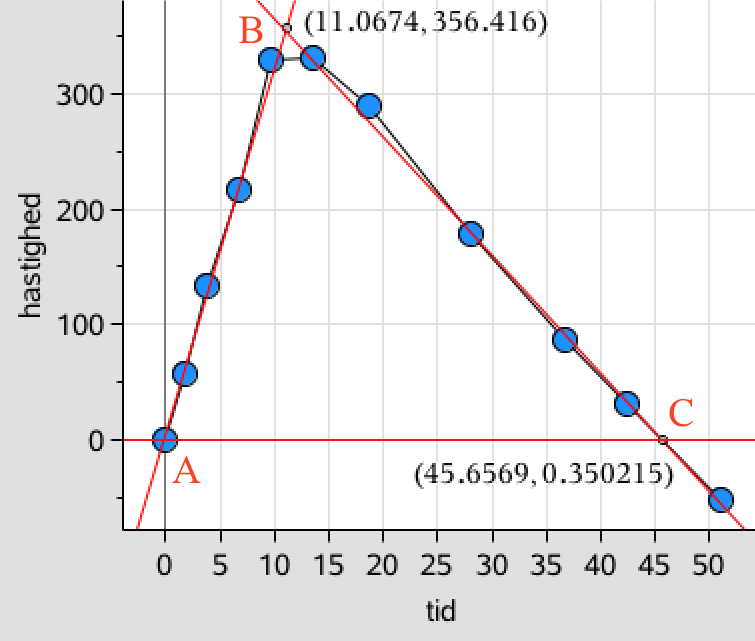
(A = starthastighed.
A-B: ret linje over x-aksen, der viser konstant acceleration opad, som skyldes rakettens brændstof.
B = største hastighed, der indtræder hvor brænstoffet slipper op.
B-C: Herefter forsætter raketten opad kun påvirket af tyngdekraften, der bremser raketten.
C = toppunkt for raketten, idet hastigheden er 0, når raketten vender.
Efter C er raketten stadig kun påvirket af tyngdekraften, der nu øger hastigheden nedad.)Trekantens areal er 0,5·højde·grundlinje = 0,5·(356,4 m/s)·(45,7 s) = 8144 m.
Dvs. rakettens maksimale højde er 8,14 km
Svar på opgave 5: Bobslæde
-
Den største fart fås for enden af banen efter, at slæden har været påvirket af tyngdekraften hele vejen ned ad banen.
Da der ikke er nogen gnidning, er den mekaniske energi bevaret, dvs. ΔEp = ΔEk, hvor ΔEp er ændringen i potentiel energi og ΔEk er ændringen i kinetisk enrgi.
Dette giver m·Δh·g = (1/2)·m·v2 ⇒ v = √[2·Δh·g], hvor Δh er højdeforskellen mellem start og mål på banen, g er tyngdeaccelerationen og v er farten.
Tallene indsættes: v = √[Δh·g·2] = √[2·(114,3 m)·(9,82 m/s2)] = √[2·114,3·9,82 m2/s2] = 47,4 m/s
Dvs. den maksimale fart er 47,4 m/s
-
Tabet i mekanisk energi (ΔEM) eller varmeskabelsen er lig med gnidningskraftens og vindmodstandskraftens arbejde over de 50 meter.
Gnidningskraftens størrelse er |FN|·μ, hvor FN er normalkraften og μ er gnidningskoefficienten. Normalkraften er på det lige vandrette stykke lig med 630 kg·9,82 m/s2 = 6187 N.
Man får at tabet i mekanisk energi er: ΔEM = (50 m)·(6187 N·0,0095 + 48 N) = 50·(6187·0,0095 + 48) J = 5338,8 J = 5,34 kJ
-
I en vandret jævn cirkelbevægelse er den resulterende kraft (FR) rettet vandret mod cirklens centrum.
Tyngdekraften er masse gange tyngdeacceleration = (630 kg)·(9,82 m/s2) = 6186,6 N. Dette er tegnet ind på figuren som FT. Den har retning lodret nedad.
Af figuren nedenunder fremgår det, at bobslædens normalretning i forhold til underlaget har en vinkel på 73° i forhold til lodret og dermed en vinkel på 90° - 73° = 17° i forhold til vandret.
Normalkraften danner en retvinklet trekant sammen med den resulterende kraft og en repræsentant for tyngdekraften som vist på figuren. Det ses, at normalkraften (FN) gange sinus til 17° er lig med tyngdekraften, dvs. |FN|·sin(17°) = 6186,6 N ⇒ |FN| = (6186,6 N)/sin(17°) = 21160 N.
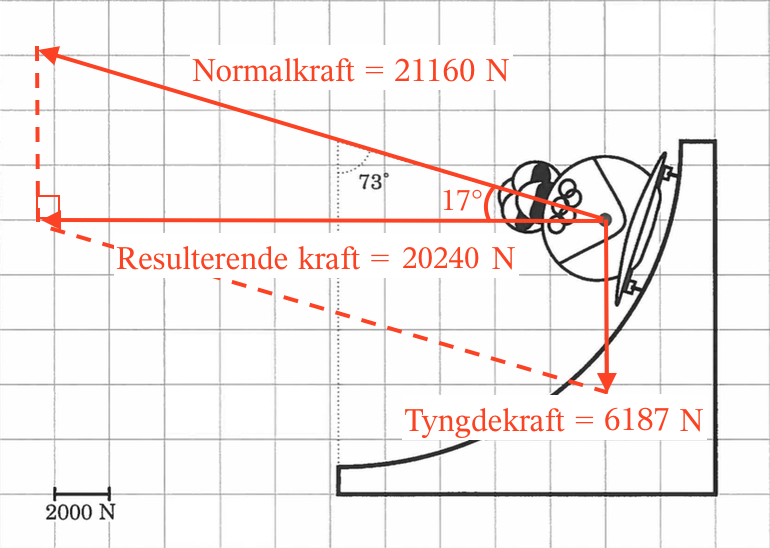
Om den resulterende kraft gælder, at...
tan(17°) = |FT|/|FR| ⇒ |FR| = |FT|/tan(17°) = 6186,6 N/tan(17°) = 20236 N.For at finde hastigheden i cirkelbevægelsen benytter man, at den resulterende krafts størrelse i en jævn cirkelbevægelse er lig med m·v2/r, hvor m er massen af bobslæde med mandskab, v er hastigheden og r er cirklens radius. Dette giver:
20236 N = (630 kg)·v2/(20 m) ⇒ v = √[(20236 N)·(20 m)/(630 kg)] = √[20236·20/630 m2/s2] = 25,35 m/s
Svar på opgave 6: Eltandbørste
-
Effekten er givet ved formlen P = U·I, hvor P er effekten, U er spændingen og I er strømstyrken. Det giver:
Effekten er 230 V·4,0 mA = 230·4,0·10-3 W = 0,92 W
-
Den inducerede spænding følger formlen: U = -N·A·(dB/dt), hvor U er den inducerede spænding, N er antal vindinger, A er tværsnitsarealet af spolen og dB/dt er ændringen af magnetfeltet med tiden til et givet tidspunkt.
Der gælder, at dB/dt kan aflæses for tidspunktet 0,01 ms ved hjælp af hældningen til nedenstående kurve af B mod t.
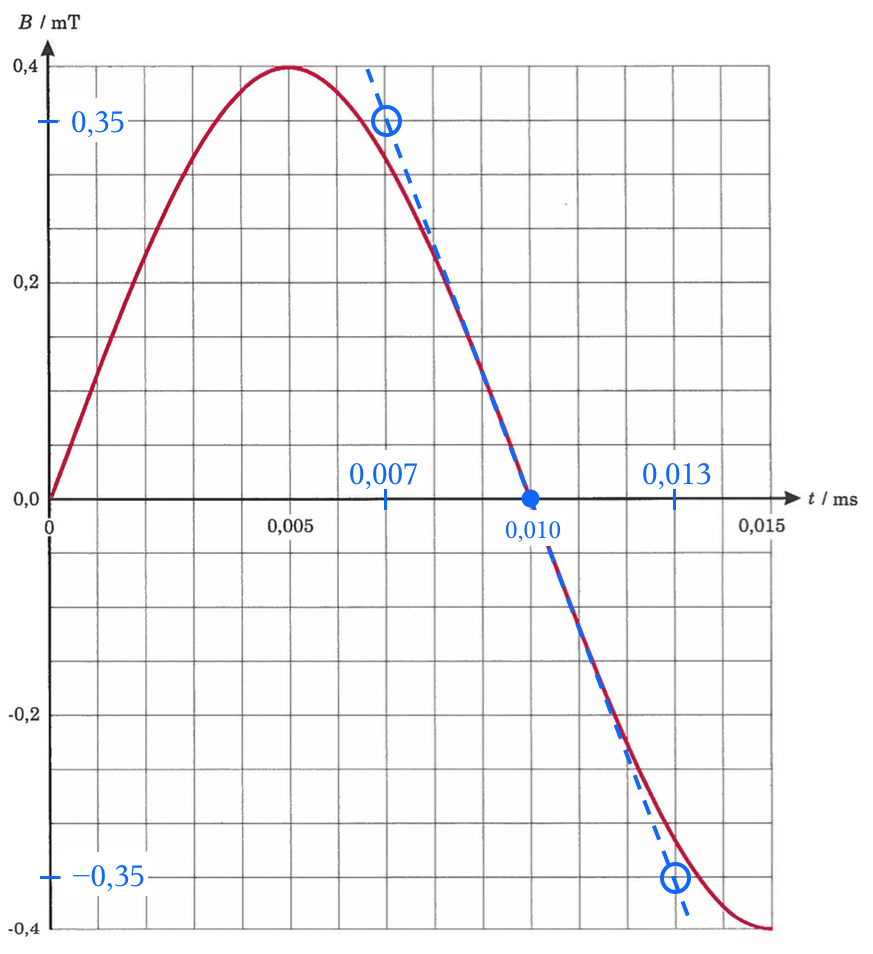
Hældningen i t = 0,010 ms ses af den blå tangent at være: [(-0,35 - 0,35) mT]/[(0,013 - 0,007) ms] = (-0,70/0,006) mT/ms = (-0,70/0,006) T/s = -117 T/s.
Dvs. den inducerede spænding i spolen til tiden t = 0,010 ms er: -82·1,8 cm2·(-117 T/s) = -82·1,8·(-117) cm2·(V⋅s/m2)/s = 17269 (0,01 m)2·(V⋅s/m2)/s = 17269·10-4 m2·(V⋅s/m2)/s = 1,7269 V = 1,73 V
Svar på opgave 7: MiniBooNE
- Der er tale om den svage vekselvirkning, da der dannes neutrinoer.
-
Da K+ mesonen er i hvile før henfaldet, er dens impuls før henfaldet lig med 0. Da der gælder impulsbevarelse er antimyonens og myonneutrinoens samlede impuls efter henfaldet også lig med 0. (Deres bevægelser er blot modsat rettede.)
Ud over impulsbevarelse skal der også gælde energibevarelse. For partiklernes energi gælder, at E2 = (m0)2·c4 + p2·c2 ⇒ E = √[(m0)2·c4 + p2·c2], hvor E er partiklens energi, m0 er partiklens hvilemasse og p er dens impuls.
Emeson = √[(493,7MeV/c2)2·c4 + 02·c2] = 493,7 MeV. K+ mesonens hvilemasse er fundet til 493,7 MeV/c2 i en tabel.
Emyon = √[(105,7 MeV/c2)2·c4 + p2·c2]. Antimyonens hvilemasse er fundet i en tabel til 105,7 MeV/c2.
Eneutrino = √[0 + p2·c2] = p·c, da myonneutrinoens hvilemasse kan sættes til 0.
Dette giver følgende energibevarelsesligning: 493,7 MeV = √[(105,7 MeV/c2)2·c4 + p2·c2] + p·c
Denne ligning løses i Ti-Nspire:
solve(493.7*mev=p*c+sqrt((105.7*mev)2+p2*c2),p) ▸ p=235.535*mev/c or mev=0.
Dvs. antimyonens impuls er p = 235,5 MeV/c