
Svar på opgave 1: Sous vide
-
Modstanden i varmelegemet findes ved hjælp af Ohm lov: U = I·R ⇒ R = U/I ⇒ (230 V)/(5,22 A) = 44,1 Ω
her er U lig med spændingsforskellen, I er strøm styrken og R er modstanden (der alle gælder for varmelegemet).
-
For at kunne løse opgaven er man nød til at antage, at sous vide'ens varmelegeme tilfører vandet energi med konstant effekt. Der ses desuden bort fra beholderens varmekapacitet.
Ved at lave en 2. gradspolynomiums regression på den målte sammenhæng mellem tid og temperatur får man den tilnærmede funktion:
T(t) = −0,00000582·t2 + 0,0380·t + 13,1 (0 ≤ t ≤ 1500). Denne funktion og målepunkterne er vist på figuren nedenunder:
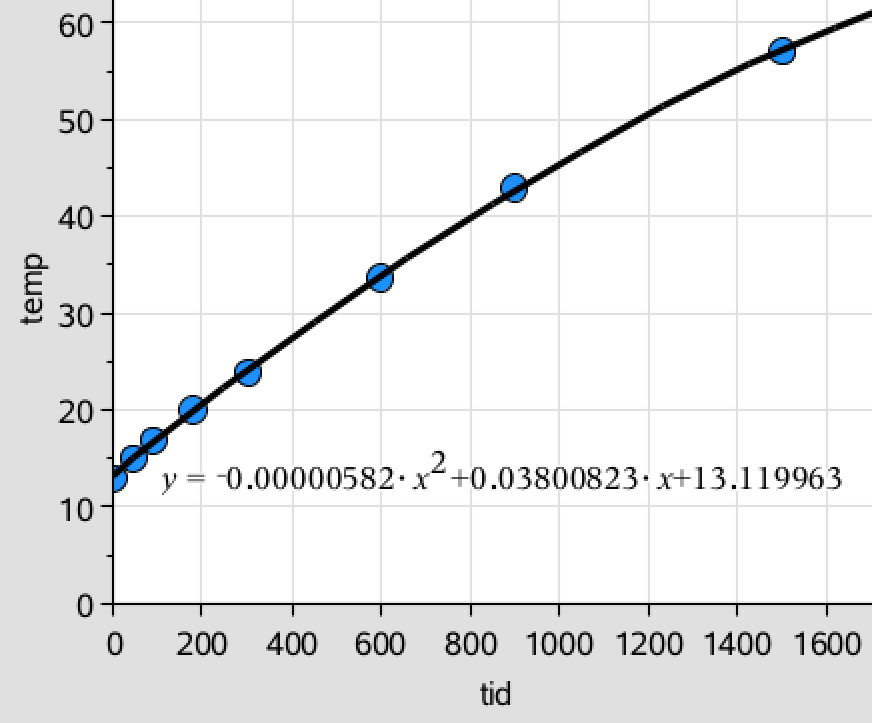
(Den rigtige sammenhæng er nærmere: T(t) = c - b·at, men den kan ikke bestemmes i CAS.)
Ved temperaturen 20,9 °C er varmelegemets effekt det eneste bidrag til temperaturændringen. Man finder det tidspunkt, hvor denne temperatur indtræder i Ti-NSpire:
solve(20.9=−5.82.*10-6*t2+0.0380*t+13.1,t)|0<t<1500 ▸ t=212
Temperaturændringen ved dette tidspunkt findes af regressionsfunktionen i Ti-Nspire:
derivative(−5.82*10−6*t2+0.0380*t+13.1,t)|t=212 ▸ 0.0355 (dvs. 0,0355 K/s)
Der gælder ved 20,9 °C, at denne temperaturændring er lig med varmelegemets effekt divideret med vandets varmekapacitet, som er (8,2 kg)·(4,182 kJ/(kg·K)) = 34,29 kJ/K.
Idet P er varmelegemets effekt, får man, at 0,0355 K/s = P/(34,29 kJ/K) ⇒
P = (0,0355 K/s)·34,29 kJ/K = 1,22 kJ/s = 1,22 kW
(Bemærk: hvis man laver lineær regression på alle data, får man en gennemsnitseffekt for varmelegeme og omgivelser lagt sammen. Denne metoder er forkert, selvom facit ser rigtigt ud.)

Svar på opgave 2: Holmium
-
I databogen ser man, at Holmium omdannes til Erbium ved β- henfald under emmision af en antineutrino. Under β- henfald omdannes en neutron til en proton i kernen af Holmium og resultatet bliver et grundstof med et højere atomnummer. Reaktionsskemaet er:
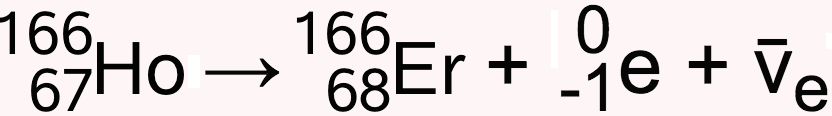
-
Man skal beregne hvor mange holmium-kerner, der henfalder og gange det antal med energien i hvert enkelt henfald. For antallet af henfald, ΔN, gælder
ΔN = N0·[1 - 0,5t/T] = A0·[T/ln(2)]·[1 - 0,5t/T],
hvor N0 = antallet af kerner fra start, A0 = aktivitet fra start, T = halveringstiden for den enkelte kerne og t er den tid, som er gået siden start. Man får med tallene indsat at:
ΔN = (5,60·109 Bq)·[(26,8 t·(3600 s/t))/ln(2)]·[1 - 0,5(24 t)/(26,8 t)] =
(5,60·109/s)·[(26,8·3600 s)/ln(2)]·[1 - 0,5(24/26,8)] = 3,605·1014 henfald.
Energien pr. henfald findes i en tabel til 1,85 MeV. De 67 % af denne energi afsættes i leveren. Dette betyder, at den energi, ΔE, som afsættes i leveren kan skrives:
ΔE = 3,605·1014·(1,85 MeV)·(67 %) = 3,605·1014·(1,85·106 eV·1,6022·10-19J/eV)·0,67 = 71,6 J

Svar på opgave 3: Pushback
-
Der gælder Ekin = 0,5·m·v2, hvor Ekin er den kinetiske energi, m er massen og v er farten af det som bevæger sig.
Ved at indsætte tallene får man: Ekin = 0,5·132000 kg·(2,63 m/s)2 = 457 kJ
-
Den resulterende kraft er summen af kræfterne. Da kraften for skub (FS) og kraften for friktion (FF) peger i modsat retning, skal deres størrelser trækkes fra hinanden. Den resulterende kraft skal være lig med m·a, hvor m er massen af flyet og a er dets acceleration, når det skubbes.
Man får: FS - FF = m·a ⇒ FS = m·a + FF = 132000 kg·1,62 m/s2 + 33 kN =
213,84 kN + 33 kN = 247 kN
-
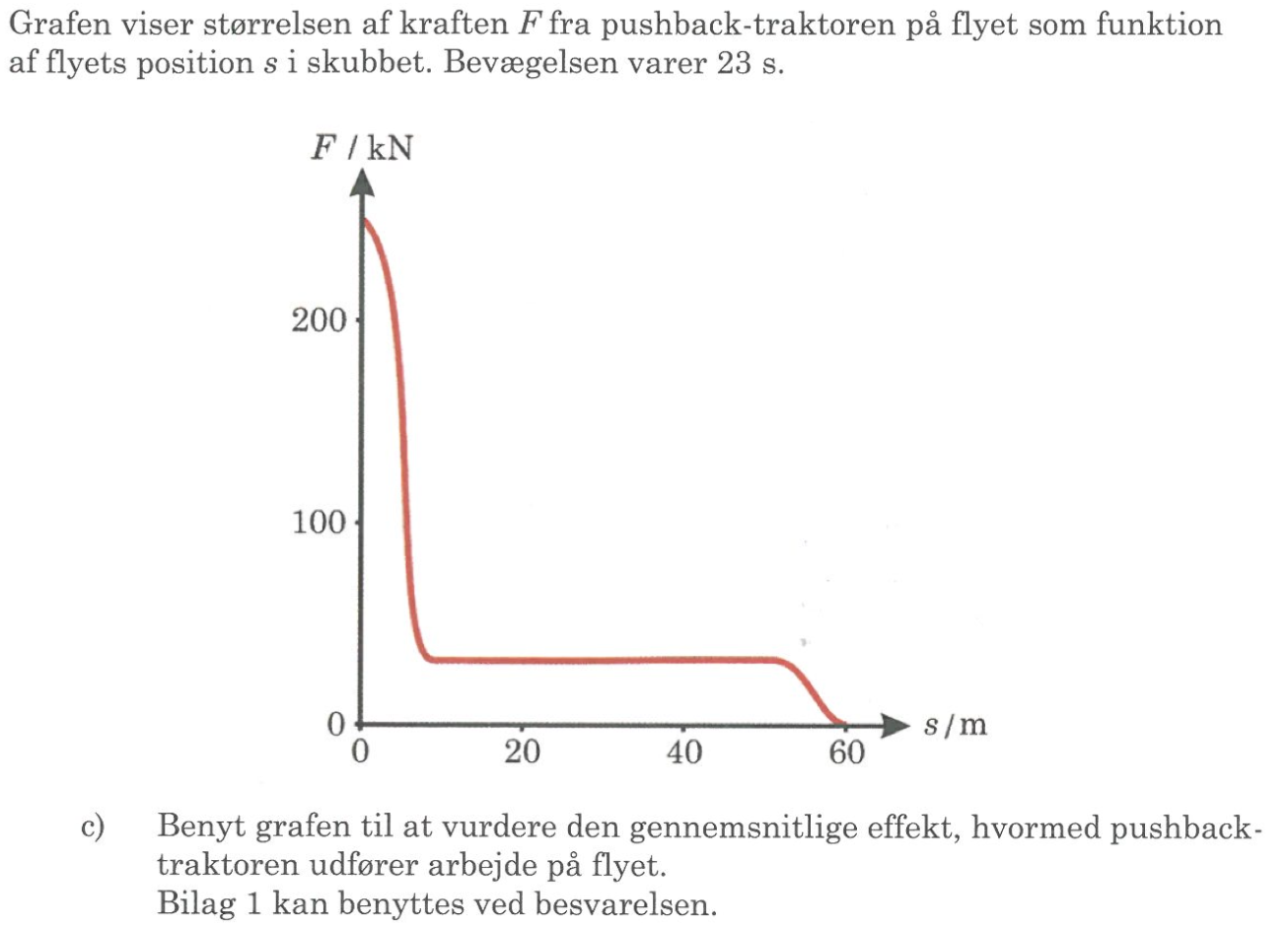
Traktorens gennemsnitlige effekt er dens samlede arbejde divideret med tiden. Det samlede arbejde findes som arealet under kurven for kraften som funktion af stedet.
Dette areal beregnes ved at lave trekanter og firkanter, der har samme samlede areal som grafen. Disse er vist nedenunder som I, II og III:
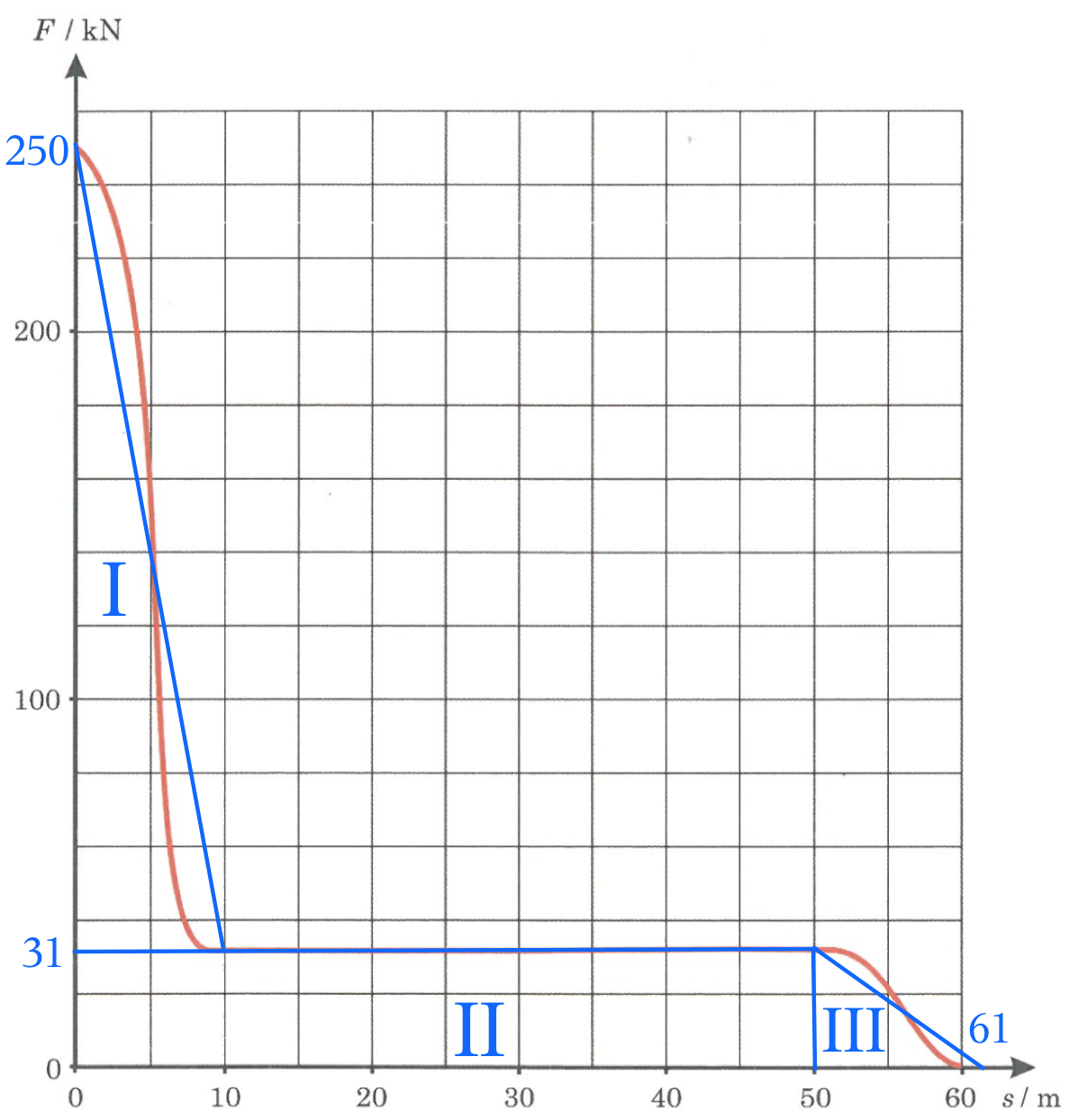
Del-arealerne er:
I: 0,5·(250 - 31)·20 kJ = 1075 kJ
II: 50·31 kJ = 1550 kJ
III: 0,5·(61 - 50)·31 = 170,5 kJ
Summen er (1075 + 1550 + 170,5) kJ = 2815,5 kJ, som er gnidningskraftes samlede arbejde.
Gnidningskraftens gennemsnitlige effekt er dermed (2815,5 kJ)/(23 s) = 122 kW

Svar på opgave 4: Urancentrifuge
-
Massen af UF6 er lig med rumfanget af gassen (= rumfanget af beholderen) ganget med gassens massefylde. Dvs. massen af UF6 gas er
(12 m)·(0,3 m)2·π·(0,64 kg/m3) = 2,17 kg
-
Centripetalkraften (FC) på UF6 molekylet er givet ved formlen:
FC = m·v2/r, hvor m er massen af molekylet, v er molekylets fart i cirkelbevægelsen og r er cirkelbevægelsens radius.
v = cirkelbevægelsens omkreds gange antal omdrejninger pr. sekund = (2·π·r)·(477/s) = (2·π·0,053 m)·(477/s) = 158,85 m/s
FC = (349 u)·(158,85 m/s)2/(0,053 m/s) = 349·(1,66·10-27 kg)·(158,85 m/s)2/(0,053 m/s) =
2,76·10-19 N

Svar på opgave 5: Lyn
-
Ladningen er strømstyrke gange tid: ΔQ = I·Δt = (40·103 A)·(2,5·103 s) = 100 C
-
For spændingsforskellen, U, der induceres i en enkelt vinding med vindingsarealet Av, gælder:
U = Av·(dB/dt) = 2,67·10-9 (T/A)·(dI/dt). Det antages, at dI/dt er konstant under hele afladningen, og at dI/dt dermed er lig med ΔI/Δt. Man får:
U = 2,67·10-9 (T/A)·(ΔI/Δt) = 2,67·10-9 (T/A)·[(40·103 A)/(60·106) s] = 1,13 m2·T/s = 1,13 V
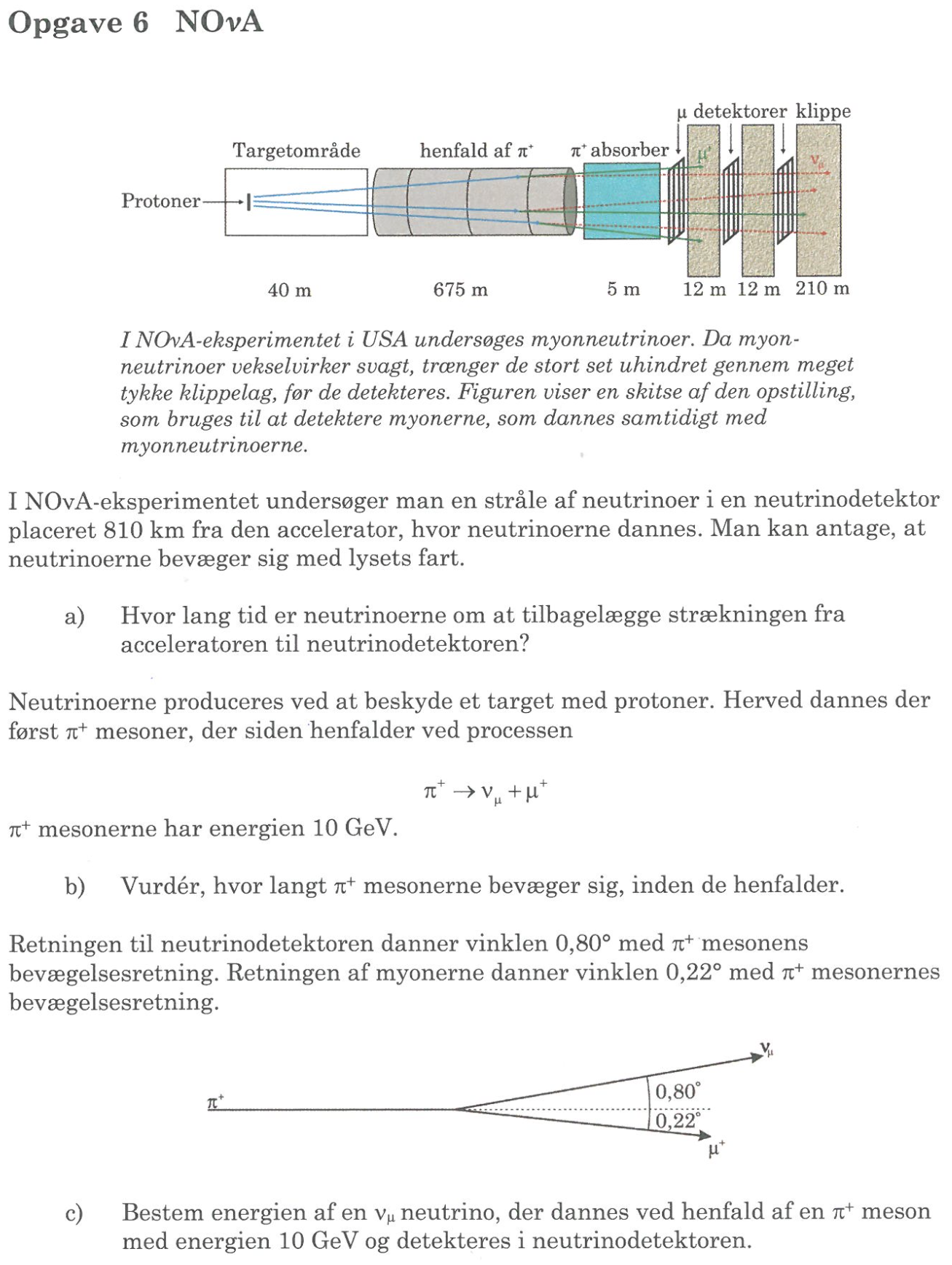
Svar på opgave 6: NOvA
-
Afstanden, som partiklen skal tilbagelægge, er (40 + 675 + 5 + 12 + 12) m = 744 m. Lyshastigheden er 3,0·108 m/s.
Den tid, som det tager at tilbagelægge strækningen, er 744/(3,0·108 m/s) = 0,25 μs
-
Man starter med at beregne pi-mesonens fart, v. Den indgår i formlen:
γ = 1/(√[1 - (v2/c2)]) hvor c er lysets hastighed og γ er gammafaktoren, som findes ud fra formlen:
ΔE = γ·mπ·c2, hvor ΔE er pi-mesonens energi og mπ er dens hvile-masse. Dette giver γ = ΔE/(mπ·c2) = (10 GeV)/((139,6 MeV/c2)·c2) = 71,63.
Pi-mesonens fart kan herefter udregnes i Ti-Nspire:
solve(71,63 = 1/sqrt(1 - (v/3,0·108)2),v) ▸ 2.9997*108
Pi-mesonens middellevetid i hvile er 2,6·10-8 s. I bevægelse er dens middellevetid = γ·2,6·10-8 s = 71,63·2,6·10-8 s = 1,86·10-6 s. Ved en hastighed på 2,9997·108 m/s vil partiklen tilbagelægge en strækning på:
(1,86·10-6 s)·(2,9997·108 m/s) = 558 m. Dette passer med det, som er vist på tegningen.
-
Der gælder, at impulsvektoren for π-mesonen skal være lig med summen af impulsvektorerne for myonen og neutrinoen. Dette er vist på tegningen:
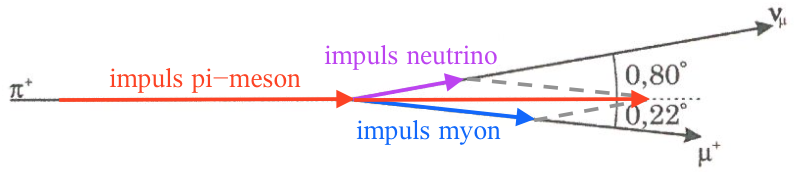
I det følgende er...
pπ pi-mesonens impulsvektor.
pμ myonens impulsvektor.
pν neutrínoens impulsvektor.
Der gælder:
|pπ| = |pν|·cos(0,80°) + |pμ|·cos(0,22°)
(længderne af komposanterne af pν og pμ parrallel med pπ er sammenlagt lig med længden af pπ.)
|pν|·sin(0,80°) = |pμ|·sin(0,22°) ⇒ |pμ| = |pν|·(sin(0,80°)/sin(0,22°))
(længderne af komposanterne af pν og pμ vinkelret på pπ er sammenlagt lig med 0.)
Tilsammen får man: |pπ| = |pν|·(cos(0,80°) + sin(0,80°)/sin(0,22°)) ⇒ |pπ| = |pν|·4,636
Pi-mesonens impuls findes ud fra dens energi, E. E2 = (mπ)2·c4 + (|pπ|·c)2 ⇒ (|pπ|·c)2 = E2 - (mπ)2·c4 ⇒
(|pπ|·c)2 = (10 GeV)2 - (139,6 MeV/c2)2·c4 ⇒ (|pπ|·c)2 = (10 GeV)2 - (139,6 MeV)2 ⇒
(|pπ|·c)2 = 99980512 MeV2 ⇒ |pπ|·c = √[99980512 MeV2] ⇒ |pπ| = 9999,03 MeV/c
Dvs. neutrinoens impuls er (9999,03 MeV/c)/4,636 = 2156,82 MeV/c. Neutrinoen har ingen hvilemasse, så dens energi bliver: (2156,82 MeV/c)·c = 2,16 GeV
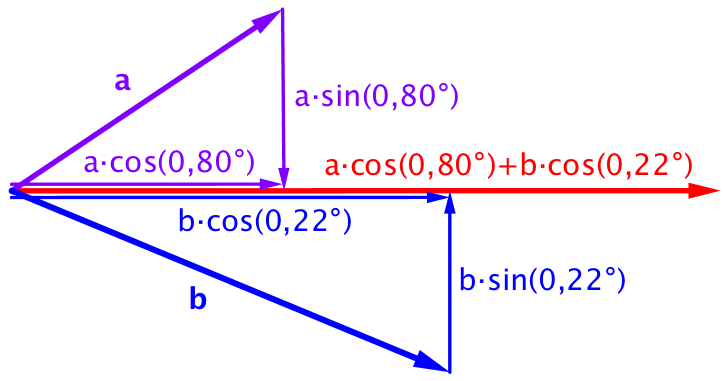
Nedenfor er vist en principtegning til at anskueliggøre beregningerne. Den røde pil er pi-mesonens impuls, a er neutrinoens impuls og b er myonens impuls. De to lodrette piler er lige store og modsat rettede.

Svar på opgave 7: Snerydning
-
Udskydningsfarten kaldes v0, og den findes ved hjælp af formlerne for det skrå kast.
Man skal gøre to antagelser for at kunne bruge disse:
I: Strålen af sne ses vinkelret fra siden.
II: Der er ingen luftmodstand.
Man har brug for to beregninger ud fra billedet:
I: vinklen, α, i forhold til vandret, som sneen slynges ud i. Den anslås til 48°.
II: sneens stighøjde (Δh), som er sneens maksimumshøjde i forhold til dysen. Den anslås til 3,0 m.
På nedenstående figur er dysens munding valgt som nulpunkt for et retvinklet koordinatsystem, og der er tegnet en sort parabel, som tilnærmer sneens kasteparabel.

Ved hjælp af formlen for stighøjden (ymaks) af et skråt kast får man:
Δh = ymaks = (v0)2·sin2(α)/(2·g) ⇒
v0 = √[Δh·(2·g)/sin2(α)] ⇒
v0 = √[(3,0 m)·(2·9,82 m/s2)/sin2(48°)] ⇒
v0 = √[(3,0·2·9,82/0,5523) m2/s2] ⇒
v0 = 10,3 m/s
Dette er sneens minimale (!) udskydningsfart. (Opgaven spørger om den maksimale fart, men når man som her ser bort fra luftmodstanden, så må man få en lavere fart end, hvis man havde medregnet den.)