Svar på opgave 1: Poselukker

1. Der gælder formlen P = U²/R, hvor

      P er effekten i watt

      U er spændingsfaldet i Volt og

      R er resistansen i Ω (ohm).

   Man får følgende i Ti-Nspire:

   solve(p=u²/r),r)|p=3.5 and u=3.2 ▸ r=2.92571

   Dvs. resistansen er 2,92571 Ω = 2,93 Ω

2. Man har formlen P = Q/Δt, hvor

      Q er varmemængde i Joule og

      Δt er tiden i sekunder.

   Varmemængden Q kan deles op i varme til opvamning (Q_op) og smeltevarme (Q_sm).

   Formlerne for hver af disse er:

      Q_op = m·c·ΔT, hvor

         m er massen af fryseposen i kg,

         c er den specifikke varmekapacitet af fryseposen i 2,3 kJ/(kg·K) og

         ΔT er ændringen i temperatur ved opvarmningen i Kelvin;
   

      Q_sm = m·L, hvor

         m er massen af fryseposen i kg og

         L er den specifikke smeltevarme i kJ/kg.

   Det antages, at starttemperaturen for opvarmningen er 20 °C.

   Man får samlet formlen: P = m·(ΔT·c + L)/Δt, som løses med hensyn til Δt (tid) i Ti-Nspire:

   solve(p=m*(δt*c+l)/tid,tid)|p=3.5*joule*sek^-1 and m=31*10^-6*kg and δt=(110-20)*kelvin and c=2.3*10³*joule*kg^-1*kelvin^-1 and l=116.6*10³*joule*kg^-1 ▸ tid=2.86617*sek

   Dvs. smeltningen tager 2,86617 s = 2,9 s

Svar på opgave 2: Galaksesuperhoben BAS11

1. Der gælder følgende formel for 1. orden afbøjningsvinklen:

   λ = d·sin(θ), hvor

      λ er lysets bølgelængde i nm

      d er gitterets linjeafstand i nm og

      θ er afbøjningsvinklen i °.

   Dette løses med hensyn til θ i Ti-Nspire:

   solve(λ=d*sin(θ*1.°),θ)|λ=520.16*10^-9*meter and d=10^-3*meter/800 and 0<θ<90 ▸ θ=24.5904

   Dvs. 1. orden afbøjningsvinklen er 24,5904° = 24,6°

2. Der gælder følgende formel for afstanden til en galakse (Hubble's lov):

   c·z = H·D, hvor

      c er lysets hastighed i m/s,

      z er rødforskydningen = 520,16-486,13)/486,13 = 0,0700,

      H er Hubble's konstant = 70 km/(s·Mpc)) = 70·10³ m/(s·10⁶·3,085·10¹⁶ m)) = 2,269·10⁻¹⁸ s^-1

      D er afstanden til galaksen.

   Dette giver i Ti-Nspire:

   solve(c*z=h*d,d)|c=3.*10⁸*meter*sek^-1 and z=0.07 and h=2.269·10^-18*sek^-1 ▸ d=9.255·10²⁴*meter

   Dvs. afstanden til BAS11 er 9,26·10²⁴ m (eller 978 mio. lysår)

   (Bemærk: Hubble's lov gælder kun for små rødforskydninger. Det vil omtrent sige for z < 1)

Svar på opgave 3: Rammemaskine

1. Der gælder følgende formel for densiteten: ρ = m/(s²·L), hvor

   ρ er densiteten i tons/m³,

      m er massen i tons,

      s er sidelængden i m og

      L er længden af pælen i m.

   Man finder ρ i Ti-Nspire:

   solve(ρ=m/(s²*l),ρ)|m=1.8*tons and s=0.3*meter and l=9*meter ▸ ρ=2.22222*tons/meter³

   Dvs. densiteten er 2,22222 tons/m³ = 2,22 tons/m³

2. Når jernklodsen har en hastighed på 2,05 m/s opad i en højde af 0,11 meter over betonpælen vil den have sammen hastighed nedad samme sted efter, at den har toppet. (Dette forudsætter, at der ikke sker tab af mekanisk energi i form af gnidning.)

   Den kinetiske energi, når den rammer pælen er lig med jernklodsens kinetiske energi i højde 0,11 meter over pælen plus dens potentielle energi i højden 0,11 m. Denne omsættes til kinetisk energi i den sidste del af faldet.

   Formlen for kinetisk energi (E_kin) er

   E_kin = 0,5·m·v², hvor

      m er jernklodsens masse i kg og

      v er farten i m/s.

   Den kinetiske energi i højden 0,11 m er

   solve(e=0.5*m*v²,e)|m=4.1*10³*kg and v=2.05*meter/sek ▸ e=8615.13*kg*meter²/sek²

   Formlen for potentiel energi (E_pot) er

   E_pot = m·h·g, hvor

      m er massen i kg,

      h er højden i forhold til et valgt nulpunkt (her 0,11 m) og

      g er tyngede-accelerationen i m/s².

   Den potentielle energi i højden 0,11 m er

   solve(e=h*m*g,e)|h=0.11*meter and m=4.1*10³*kg and g=9.82*meter/sek² ▸ e=4428.82*kg*meter²/sek²

   Jernklodsens samlede kinetiske energi, når den rammer pælen, er:

   8615,13 kg·m²/s² + 4428,82 kg·m²/s² = 8615,13 J + 4428,82 J = 13,0 kJ

3. Kranens arbejde (A) er lig med friktionens arbejde (A_f) plus tilvæksten i potentiel energi (E_p) ved løftet.

   Man finder friktionens arbejde som arealet under kurven fra s = 0 til s = 7,5 m.

   

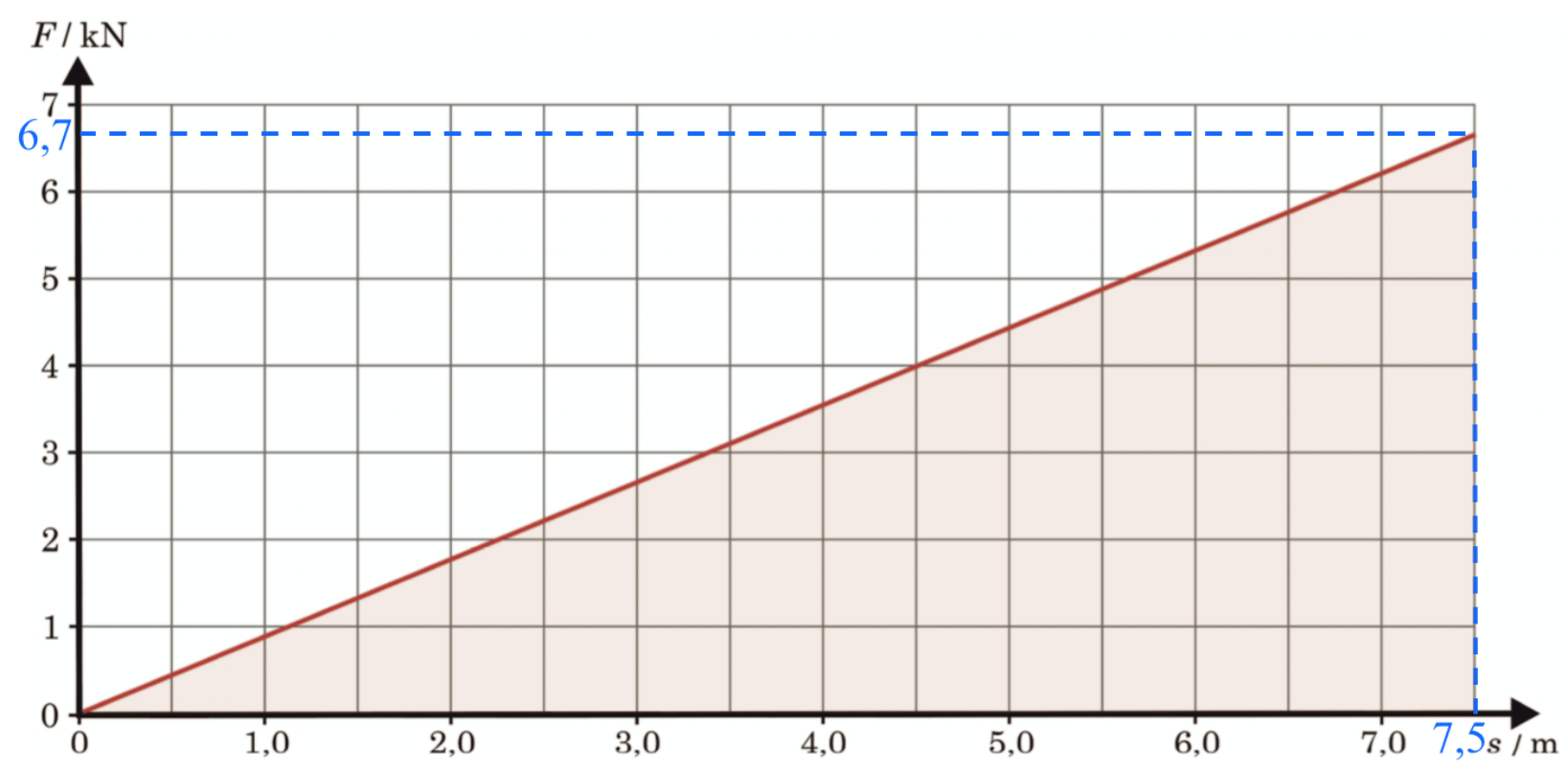
   Som det ses på billedet ovenfor (markeret med brunt), er dette lig med arealet af en retvinklet trekant med kateterne 7,5 og 6,7.

   Man får: A_f = 0,5·(7,5 m)·(6,7 N)·10³ = 25125 J

   Hertil kommer ændringen i potentiel energi: E_p = (7,5 m)·(1,8·10³ kg)·(9,82 m·s^-2) = 132570 J.

   Det samlede arbejde, som kranen udfører ved at løfte pælen op ad jorden bliver: A = A_f + E_p = (132570 + 25125) J = 157695 J = 157,7 kJ

Svar på opgave 4: Kryptonlampe

1. I følge en tabel foregår henfaldet ved beta-henfald (det gælder for de fleste radioaktive isotoper). Man får:

   

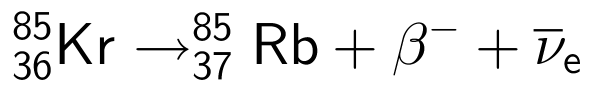
2. Man skal bruge formlen for massen (m), som er

   m = m₀·e^-k·t. Her er

      m₀ er startmassen,

      k er aktivitetskonstanten og

      t er tiden siden start.

   Man har formlen startmassen: m₀ = (A₀/k)·m_n,

      A₀ er startaktiviteten i s^-1 og

      m_n er massen af den pågældende nukleotid.

   Den samlede formel for m som funktion af tiden er: m(t) = (A₀/k)·m_n·e^-k·t

   Der gælder i øvrigt formlen: k = ln(2)/T_1/2

   Dette giver følgende i Ti-Nspire med hensyn til massen efter 5 år:

   solve(m=(a0/k)*mn*e^−k*t,m)|a0=2000*sek^-1 and mn=85*1.661*10^-27*kg and k=(ln(2)/t_halv) and t_halv=10.7*år and t=5*år and år=365.25*24*3600*sek ▸ m=9.94976*10⁻¹⁴*kg

   Dvs. efter 5 år er massen af Krypton lig med 9.94976·10⁻¹⁴ kg = 9,95·10⁻¹⁴ kg

Svar på opgave 5: RHIC

1. Man skal bruge formlen v = Δs/Δt, hvor

      v = fart i m/s,

      Δs = strækning i m og

      Δt = tid i s.

   Dette løses i Ti-Nspire med hensyn til t:

   solve(v*t=s,t)|v=2.997*10²*meter/mikrosek and s=3834*meter ▸ t=12.7928*mikrosek

   Dvs. det tager 12,7928 μs = 12,8 μs for guldionen at nå rundt i ringen.

2. Når en ladning bevæger sig i et ensartet elektrisk felt, kan man bruge formlen:

   q·U = ΔE_kin, hvor

      q er ladningen i Coulomb,

      U er spændingsforskellen i volt og

      ΔE_kin er ionens ændring i kinetisk energi.

   For ladningens kinetiske energi gælder:

   E_kin = 0,5·m·v², hvor

      m er ionens masse i kg og

      v er dens fart i m/s.

   Dette giver den samlede formel for v: q·U = 0,5·m·v². Denne ligning løses i Ti-Nspire:

   solve(q*u=0.5*m*v²,v)|q=1.6*10^-19*coulomb and u=14*10⁶*kg*meter²/(sek²*coulomb) and m=(196.97/(6.023*10^-23))*10^-3*kg ▸ v=3.70122·10⁶*meter/sek or v=−3.70122·10⁶*meter/sek

   Dvs. guldionens fart er 3,70122·10⁶ m/s = 3700 km/s, når den rammer foliet.

3. Når ladede partikler som ioner bevæger sig vinkelret på et magnetfelt gælder formlen:

   F = v·q·B, hvor

      F er kraften på ionen i N,

      v er ionens fart i m/s,

      q er ionens ladning i Coulomb og

      B er magnetfeltets styrke i Tesla (T = kg/(C·s)).

   Magnetfeltet styrke beregnes i Ti-Nspire:

   solve(f=v*q*b,b)|f=12.995*10⁻⁹*kg*meter*sek^-2 and v=2.997*10⁸*meter*sek^-1 and q=79*1.6*10^-19*coulomb ▸ b=3.43038*kg/(coulomb*sek)

   Dvs. magnetfeltets størrelse er 3,43038 kg/(coulomb*sek) = 3,43 T

Svar på opgave 6: Ξ_b^*0 baryonen

1. For den stærke vekselvirkning gælder at man kan finde kvarksammensætningen af den henfaldne partikel ved at lægge kvarkerne sammen for de danne partikler. En kvark går ud mod den tilsvarende anti-kvark.

   π⁺-mesonen kvarksammensætning slås op til: ud̅ (up-antidown).

   Man lægger dsb (down-strange-bottom) og ud̅ (up-antidown) sammen og får usb (up-strange-bottom).

   Dvs. Ksi-baryonen har kvarksammensætningen usb

2. Ved henfaldet gælder energibevarelse. Desuden er energien for de to myoner ens:

   E_μ = 0,5·E_J/Ψ. Her er

      E_μ energien for hver af de to myoner (μ⁺ og μ^-), mens

      E_J/Ψ er energien for J/Ψ-mesonen.

   Der gælder desuden for hver af myonerne E² = m²·c⁴ + p²·c², hvor

      E er den enkelte myons energi i MeV,

      m er den enkelte myons masse i MeV/c²,

      c er lysets hastighed (dens værdi i m/s skal ikke bruges) og

      p er den enkelte myons bevægelsesmængde i MeV/c.

   Man finder bevægelsesmængden for hver af myonerne i Ti-Nspire:

   solve(e²=m²*c⁴+p²*c²,p)|e=1558.5*mev and m=105.7*mev/c² ▸ p=1554.91*mev/c or p=−1554.91*mev/c

   Dvs. den enkelte myons bevægelsesmængde er 1554,91 MeV/c = 1555 MeV/c

Svar på opgave 7: Bodyflight

1. Man bruger følgende formel for frit fald med luftmodstand (der er flere muligheder):

   F = (1/2)·p·c·A·v², hvor

      F er luftens kraft i N,

      ρ er luftens densitet i kg/m³,

      c er personens enhedsløse formfaktor og

      A er personens areal vinkelret på luftstrømmen i m² og

      v er personens fart i forhold til luften i m/s.

   For frit fald med luftmodstand gælder: v_t = √[2·m·g/(ρ·c·A)], hvor

      v_t er terminalhastigheden, dvs. den hastighed, der gør, at luftens kraft på personen er lig med tyngdekraten.

   Når denne hastighed i forhold til luften nås, vil den resulterende kraft på personen være 0, og der vil ikke foregå yderligere acceleration.

   Hvis luften ikke bevæger sig i lodret retning, vil dette betyde, at personen bevæger sig med jorden med konstant fart. For en lodret vindtunnel (som her) vil det betyde, at personen ligger stille i forhold til jorden.

   Man har, at g = 9,82 m/s².

   Man antager, at m = 60 kg og

   A = (1,5 m)·(0,4 m) + (0,7 m)·(0,1 m) = 0,67 m²

   (Det ses af billedet, at personen bøjer benet opad, så det kun er ca. 1,5 m af kroppen, der står vinkelret på luftstrømmen. Desuden er armende rakt ud. De er ca. 0,7 m lange og 0,1 m brede.)

   Formfaktoren afhænger af personens form, og hvor glat tøjet er. Den sættes til 0,8.

   Luftens densitet sættes til 1,0 kg/m³

   Man får:

   solve(v=sqrt(2*m*g/(p*c*a)),v)|m=70*kg and g=9.82*meter*sek^-2 and p=1.*kg*meter^-3 and c=0.8 and a=0.67*meter² and meter=0.001*km and sek=(1/3600)*time ▸ v=182.322*|km/time|

   Dvs. den opadgående luftstrøms fart er 182,322 km/time = 182 km/t

   (I følge Copenhagen Air Experience, så blæser luften i deres vindtunnel opad med op til 220 km/t.)