Svar på opgave 1: Isbjørn på isflage

1. Man skal undersøge om den maksimale opdrift på isen kan bære både isflage og bjørn. Dette svarer til at undersøge om den maksimale masse af vand, som isflagen kan fortrænge (m_v-max) minus massen af isflagen (m_i) er større end isbjørnens masse.

   Man har formlen: m_v-max = V_i·ρ_v, hvor

      V_i er volumenet isflagen i m³ og

      ρ_v er densiteten af havvand i kg/m³.

   Man får, at den maksimale opdrift på isflagen er

   V_i·(ρ_v - ρ_i) = (18 m³)·(1025 kg·m^-3) = 18·1025 kg·m^3-3 = 18450 kg.

   Denne opdrift skal kunne bære isflagens masse (m_i) og isbjørnens masse.

   m_i = V_i·ρ_i, hvor ρ_i er densiteten af isflagen i kg/m³.

   Isens densitet sættes til 900 kg/m³. Dermed er isflages masse: m_i = (18 m³)·(900 kg/m³) = 16200 kg. Dette giver den samlede masse for isflage og bjørn: 16200 kg + 450 kg = 16650 kg.

   Da dette er mindre end den maksimale opdrift på 18450 kg, så kan isflagen bære isbjørnen.

Svar på opgave 2: Stjernestøv

1. Gravitationskraften er

   F = (G·m_s·m_j)/r², hvor

      G er gravitationskonstanten i m³·s^-2·kg^-1,

      m_s er massen af sonden i kg,

      m_j er massen af jorden i kg og

      r er afstanden mellem sondens massemidpunkt og jordens centrum. Denne er lig med

         jordens radius (r_j) plus den højde over jordoverfladen, som sonden befinder sig i.

   G slås op til: 6,67408·10^-11 m³·s^-2·kg^-1.

   Jordens masse slås op til: m_j = 5,972·10²⁴ kg.

   Jordens radius slås op til: r_j = 6371 km

   Afstanden fra jordens centrum til satelitten = r = (6371 + 125) km = 6496 km

   F = (6,67408·10⁻¹¹ m³·s^-2·kg^-1)·(45 kg)·(5,972·10²⁴ kg)/(6496·10³ m)² = 0,42504 kN

   Dvs. gravitationskraften på sonden er 0,43 kN

2. Gnidningskraftens effekt er mindskelsen i mekanisk energi pr. tidsenhed. Man får

   Start:

      Kinetisk energi = 0,5·(45 kg)·((46300·10³ m)/(3600 s))² = 3,72168 GJ

      Potentiel energi = (−6,67408·10^-11 m³·s^-2·kg^-1)·(45 kg)·(5,972·10²⁴ kg)·(6496·10³ m)^-1 =

         -2,76107 GJ

      Mekanisk energi = E_m,start = 3,72168 GJ - 2,76107 GJ = 0,96061 GJ

   Slut:

      Kinetisk energi = 0.5·45 kg·((15·10³ m)/(3600 s))² = 390,625 J

      Potentiel energi = −6.67408·10^-11 m³ s^-2 kg^-1·45 kg·5,972·10²⁴ kg·(6371·10³ m)^-1 =

         -2,81524 GJ

      Mekanisk energi = E_m,slut = 390,625 J - 2,81524 GJ = -2,81523961 GJ

   Ændring i mekanisk energi uden fortegn (|ΔE_m|) bliver:

   |ΔE_m| = |E_m,slut - E_m,start| = |−2,81524 GJ - 0,96061 GJ| = 3,77585 GJ

   Tiden omskrives fra minutter til sekunder: 13 min. = 13·60 s = 780 s

   Dvs. den gennemsnitlige effekt som gnidningskraften har brugt til at omsætte mekanisk energi til varme er:

   P = (3,77585 GJ)/(780 s) = 4,8408333 MJ/s = 4,84 MW

Svar på opgave 3: Flerovium

1. På nedenstående (afstemte) reaktionsskema er antallet af nukleoner (protoner + neutroner) for hver nuklid eller partikel fremhævet med rødt:

   

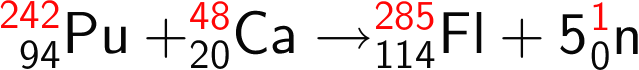
   Antallet af neutroner skal være ens på begge sider. Det ses, at lægges nukleoner sammen på venstre side fås: 242 + 48 = 290. På højre side fås: 285 + antal neutroner, hvilket vil sige, at antallet af (frigivne) neutroner som vist skal være 5

2. Massen af en Fl-285 isotop er massen af Cn-281 isotopen plus massen af en alfa-partikel plus massedefekten ved fissionen.

   Cn-281 masse: 281,16929 u

   Alfa-partikel masse: 4,002603250 u

   Massedefekten eller den masse (m_d), der bliver til energi, findes af formlen:

   Q = m_d·c² ⇒ m_d = Q/c²

   Der er opgivet følgende:

   Q = 1,762·10^-12 J = 1,762·10^-12 kg·m²·s^-2

   c = 2,99792458·10⁸ m/s

   Desuden gælder omskrivningen: u = 1,66053873·10^-27 kg ⇒ u/(1,66053873·10^-27 kg) = 1.

   Man får massedefekten til:

   m_d = ((1,762·10^-12 kg·m²·s^-2)/(2,99792458·10⁸ m·s^-1)²)·(u/(1,66053873·10^-27 kg)) =

   0,011806346 u

   Man får summen af masser og massedefekt: 281,16929 u + 4,00260325 u + 0,011806346 u = 285,171893 u

   Dvs. massen af Fl-isotopen bliver med fire betydende cifre: 285,2 u

Svar på opgave 4: PET-scanning

1. Fotonens energi (E) er E = p_foton·c

   p_foton er fotonens bevægelsesmængde = 2,73·10^-22 kg·m/s

   c er lysets hastighed = 3,00·10⁸ m/s

   solve(e=p*c,e)|p=2.73*10^-22*kg*meter*sek^-1 and c=3.*10⁸*meter*sek^-1 and kg=joule/meter^-2*sek² ▸ e=8.19*10^-14*joule

   Dvs. fotonens energi er 8,19·10^-14 J

2. Positonens bevægelses mængde er lig med vektorsummen af fotonernes bevægelsesmængde, idet man forudsætter bevægelsesmængdebevarelse.

   Dvs. at vektorsummen af fotonernes bevægelsesmængde skal være lig med (vektoren for) bevægelsesmængden af positronen. Kraftdiagrammet er vist nedenunder (vinklen er fortegnet).

   

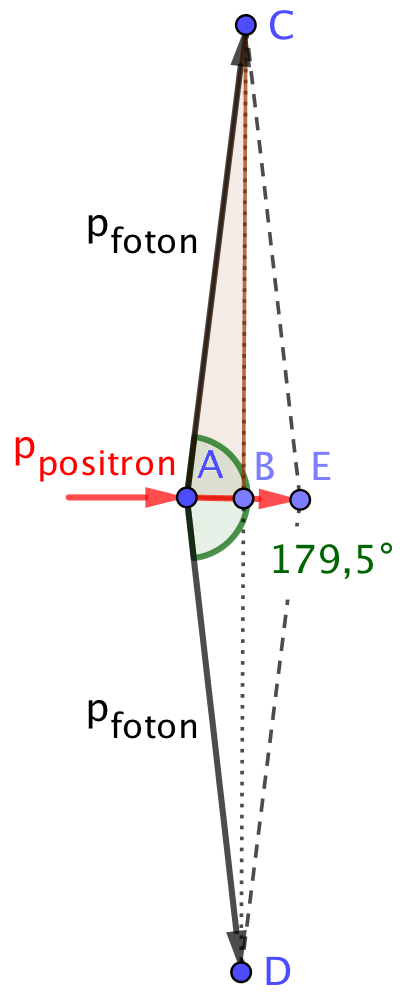
   Da de to fotoner har samme bevægelsesmængde, så udspænder deres vektorer en rombe.

   Skæringspunktet mellem rombens diagonaler kaldes B. Summen af fotonernes bevægelsesmængdevektorer er vektor AE = 2·AB.

   Trekant ABC er retvinklet og ∠A = 179,5°/2 = 89,75°. |AB| = |p_foton|·cos(∠A) dvs.:

   p_positron = 2·p_foton·cos(89,75°) =

   2·2,73·10^-22·cos(89,75°) kg·m/s = 2,38236687·10^-24 m·kg/s

   Dvs. positronenes bevægelsesmængde er 2,38·10^-24 m·kg/s

3. Aktiviteten som funktionen af tiden (A(t)) for henfaldsprocessen af Flour-isotopen følger formlen:

   A(t) = A₀·exp(-k·t), hvor

      A₀ er begyndelsesaktiviteten i Bq (= s^-1)

      k er aktivitetskonstanten i s-1 og

      t er tiden, der er forløbet siden det valgte starttidspunkt i s.

   k=ln(2)/T_0,5, hvor

      T_0,5 er halveringstiden for F-isotopen. Denne slås op til: 109,7 min. Man får:

   k=ln(2)/T_0,5 = ln(2)/(109,7 min.) = ln(2)/(109,7·(60 s)) = ln(2)/(109,7·60) s^-1 = 0,00010531 s^-1

   A₀ = 400 MBq = 400·10⁶ s^-1

   Man skal integrere aktiviteten over 40 minutter = 40·60 s = 2400 s. Dette gøres i Ti-Nspire:

   integral(a_0·exp(-k·t),t,0,2400*sek)|a_0=400*10⁶*sek^-1 and k=1.0531·10^-4/sek ▸ 8.48289116·10¹¹

   Dvs. antallet af annihilationsprocesser på 40 minutter er 8,5·10¹¹

Svar på opgave 5: Candyfloss

1. I = (1100 W)/(230 V) = 4,78 A

2. Man har formlen for den tid (Δt), som det tager at smelte sukkeret er

   P·Δt = Q ⇒ Δt = Q/P, hvor

      Q er varmen i J og

      P er effektet af varmelegemet i W.

   (Det forudsættes, at der ikke er varmetab til omgivelserne).

   Formlen for Q er:

   Q = c_s*ΔT·m_s + L_s·m_s, hvor

      c_s er sukkerets specifikke varmekapacitet i J/(kg·K),

      m_s er massen af sukker i kg

      L_s er den specifikke smeltevarme for sukker i J/kg.

   Det giver i Ti-Nspire: Q = ((1.5*joule)/(10^-3*kg*kelvin))*(186*kelvin-26*kelvin)*0.03*kg+((130*joule)/(10^-3*kg))*0.03*kg ▸ 11100.*joule

   Tid = Q/P = (11100 J)/(1110 W) = 11100/1110 J/W = 10 J/(J/s) = 10 s

   Dvs. det tager 10 s at smelte sukkeret til en candyfloss.

3. Det forudsættes, at der ikke er luftmodstand og at tyngdekraften er så lille, at man kan se bort fra den.

   Centripetalkraften (F_c) er F_c = -4·pi·m·f²·r, hvor

      f er antallet af omdrejninger af roternde hjul pr. sek

      m er massen af dråben i kg

      r er radius af roterende hjul i m.

   Massen er 30*10^-3 kg/1000 = 3,0*10^-5 kg

   Radius = 0,071 m.

   Man finder f i Ti-NSpire:

   solve(fc=4*π²*m*f²*r,f)|fc=0.28*newton and m=3.*10^-5*kg and r=0.071*meter and newton=kg*meter*sek^-2 and sek=minut/60 ▸ f=3462.26732/minut or f=−3462.26732/minut

   Dvs. den foretager 3500 omdrejninger pr. minut

Svar på opgave 6: Strømningshastighed

1. Kraften på en elektron, der bevæger sig i et magnetfelt vinkelret på feltet, følger formlen:

   F = q·v·B, hvor

      F er kraften i Newton,

      q er lektronens ladning i Coulomb (tabelværdi: 1,60·10^-19 C),

      v er elektronens fart i m/s (opgivet til: 0,25 m/s) og

      B er magnetfeltets størrelse i Tesla (opgivet til: 65·10^-3 T).

   (Kraften er både vinkelret på elektronens bevægelsesretning og magnetfeltet, dvs. det peger mod en af elektroderne).

   Der gælder følgende omskrivningen mellem enhederne: T = N·s·C^-1·m^-1 ⇒ N = T·s^-1·C·m.

   Man får: F = (1,6·10^-19 C) ·(0,25 m·s^-1)·65·10^-3 T = 2.6·10^-21 N

   Dvs. kraften på elektronen er 2,6·10^-21 N

2. For spændingen og elektroder hvorimellem, der bevæger sig en ladning parallelt med elektroderne og vinkelret på et magnetfelt:

   U = B·l·v, hvor

      U er spændingen mellem elektroder i volt (opgivet til 105·10^-6 V),

      l er udstrækningen af strømmen af ioner på tværs af magnetfeltet og på tværs af

         bevægelsesretningen i m og

      v er farten af ioner i m/s.

   L er blodårernes diameter, som er opgivet til 4,75·10³ m.

   Desuden har man omskrivningen: T=V·s/m². Man får:

   solve(u=b*l*v,v)|u=105*10^-6*volt and l=4.75*10^-3*meter and b=65*10^-3*tesla and tesla=volt*sek/meter² ▸ v=0.340080972*meter/sek

   Dvs. blodets fart vurderes til 0,34 m/s

   Det forudsættes at afstanden mellem elektroderne er lille i forhold til elektrodernes længde i ionernes bevægelsesretning, så man kan se bort fra randeffekter for elektroderne.

Svar på opgave 7: Ω^- partiklens masse

1. Kvarksammensætning:

   Ω^- (Omega-minus baryon): sss

   Ξ⁰ (Ksi-nul baryon): uss

   π^- (pi-minus meson eller negativ pion): du̅

   Når man lægger kvarkerne på venstre side sammen, så får man: dss, idet u (up) og u̅ (anti-up) går ud med hinanden. Samlet ændring af kvarksammensætningen er sss → dss.

   Dette viser, at der er tale om den svage vekselvirkning, da en ændring af den samlede kvarksammensætning (en flavourændring) kun kan ske for denne.

2. Der forudsættes, at gælde energibevarelase ved henfaldet, så Omega-partiklens energi er lig med summen af energierne af Ksi- og pi-partiklerne:

   E_Ω = E_Ξ + E_π = 2320 MeV + 313,8 MeV = 2633,8 MeV

   Der gælder formlen E² = m²·c⁴ + p²·c²

   Man finder massen af Omega-partiklen i Ti-Nspire:

   solve(e²=m²*c⁴+p²*c²,m)|e=2633.8*mev and p=2029*mev/c ▸ m=1679.30386*mev/c² or m=−1679.30386*mev/c²

   Dvs. Omega-partiklens masse er 1679 MeV/c²