Svar på opgave 1: Is på højspændingsledninger

1. Effekten er P = U·I = R·I², hvor

      P er lig med effekten i W,

      U er spændingen i V og

      I er strømstyken i A. Det giver

   Effekten = (1,53 Ω)·(105 A)² = 16.868,3 A²·Ω = 16,9 kW

2. Energien (forkortet Q og målt i J) bruges til opvarmning og smeltning.

   Q = m·c_i·ΔT + m·L_i, hvor

      m er masse af is i kg,

      c_i er den specifikke smeltevarme for is (ved -5) °C i J/(kg·K),

      ΔT er temperaturforskellen ved opvarmning i K og

      L_i er isens smeltevarme i J/kg.

   Is specifikke varmekapacitet ved -5 °C slås op til 2,06 kJ/(K·kg).

   Is smeltevarme slås op til 334 kJ/kg. Man får:

   Q = (4,2·10⁴ kg)·[2,06·10³ J/(K·kg)]·(10 K) + (4,2·10⁴ kg)·(334·10³ J/kg) = 14,8932 GJ.

   Dvs. den tilførte varme er 14,9 GJ

Svar på opgave 2: CINDI

1. Det foreløbige reaktionsskema er:

   

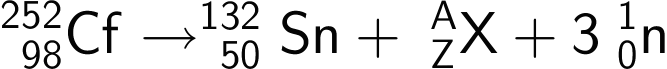
   Her er X det ukendte grundstof, A er dets massenummer og Z dets atomnummer.

   Ser man på massenumrene får man: A = 252 - 132 - 3 = 117, idet antallet af nukleoner bevares ved reaktionen

   Ser man på atomnumrene får man: Z = 98 - 50 = 48 (Cd), idet protonerne også skal være bevaret.

   Dette giver det endelige reaktionsskema:

   

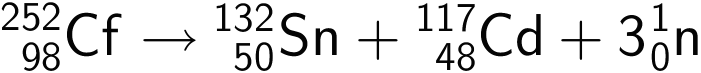
   Q = m·c², hvor m er massedefekten ved reaktionen. (Ved kernereaktioner gælder ikke massebevarelse, det gør der kun ved kemiske reaktioner, der foregår i den yderste del af elektronskyen.)

   Massedefekten er lig med massen efter reaktionen minus massen før.

   Atomasserne for isotoperne og neutronen slås op i en tabel:

   masse af Cf-252: 252,081626 u

   masse af Sn-132: 131,917816 u

   masse af Cd-117: 116,907219 u

   masse af neutron: 1,008664916 u

   Massedefekt = 252,081626 u - (131,917816 u + 116,907219 u + 3·(1,008664916 u)) = 0,230596 u. Man får:

   Q = (0,230596 u)·c² = (0,230596·931,494 MeV/c²)·c² = 214,8 MeV

2. Henfaldet er en blanding af alfa-henfald og spontan fission.

   Halveringstid for henfaldet = 2,65 år i følge tabel.

   Henfald = ændring i antal Cf-atomer. Formlen for antallet af Cf-atomer (N(t)) er:

   N(t) = N₀·(1/2)^t/T, hvor

      N₀ er antallet af atomer fra start,

      t er tiden fra det valgte starttidspunkt i år og

      T er halveringstiden for henfaldet af Cf-252 i år.

   Ændringen i antal atomer er N(0) - N(15) =

   N₀ - N₀·(1/2)^t/T = N₀·(1 - (1/2)^t/T) =

   [(500·10^-6·10^-3 kg)/(252,0816 u)]·[1 - (1/2)^{(15 år)/(2.65 år)}] =

   [(500·10^-6·10^-3 kg)/(252,0816·1,661·10^-27 kg)]·[1 - (1/2)^5,66038] = 1,17054·10¹⁸

   Antallet af dannede neutroner er antallet af henfald gange andelen af neutroner ved henfaldet, dvs:

   0,0309·3,79·1,17054·10¹⁸ neutroner = 1,37·10¹⁷ neutroner

Svar på opgave 3: Kvasaren 3C-279

1. Kvasarer er fjerne objekter og fjerner sig fra jorden på grund af universets udvidelse, Man bruger formlen for kosmologisk rødforskydning:

   a_nu/a_før = 1 + z, hvor

      a_før er afstanden til kvasaren før i lysår,

      a_nu er afstanden til kvasaren nu i lysår og

      z er rødforskydningen.

   Man skal finde Δa = a_nu - a_før.

   Ud fra formlen får man: a_nu/a_før = 1 + z ⇒ a_før = a_nu/(1 + z) ⇒

   Δa = a_nu - a_før = a_nu - a_nu/(1 + z) = a_nu·z/(1 + z). Tallene indsættes:

   Δa = 5,67·10⁹·0,538/1,538 ly = 1,98339·10⁹ ly

   Dvs. afstanden mellem jorden og kvasaren er øget med 1,98·10⁹ lysår i den tid, der er gået siden lyset blev udsendt.

Svar på opgave 4: Luftskib

1. Effekten (P) fra motoren følger formlen:

   P = A·P_a·η, hvor

      A er solfangerens overfladeareal,

      P_a er effekten fra solen pr. m³ af solcellerne og

      η er solcellernes nyttevirkning.

   Dvs. effekten fra motoren er = (750 m²)·(800 W·m^-2)·0,25 = 150000 W = 150 kW

2. Nyttelasten (M_n) er opdriften (kaldet M_o og opfattet som en masse) minus massen af luftskib og helium (M_s+h). Man får:

   Opdrfiten findes som massen af fortrængt luft.

   Dvs. M_o = V_s·ρ_l, hvor

      V_s er volument af lustskibet og

      ρ_l er luftens densitet.

   Man får samlet formlen: M_n = V_s·ρ_L - M_s+h

   Tabelværdier: ρ_l = 1,293 kg/m³ (ved 0 °C)

   Med de øvrige værdier fra opgaven indsat får man:

   Nyttelast = (8,4·10³ m³)·(1,293 kg/m³) - 8,0·10³ kg = 2861,2 kg = 2860 kg

   (Det bemærkes, at havde man valgt luftens densitet ved en højere lufttemperatur, så ville opdriften og dermed også nyttelasten have været mindre).

3. Det antages, at motorens kraft (F_m) er lig med kraften fra luftmodstanden (F_l), således at luftskibet ikke har nogen resulterende kraft på sig og dermed bevæger sig med konstant fart.

   Kraften fra luftmodstanden følger formlen:

   F_l = 0,5·ρ_l·A·c·v², hvor

      ρ_l er luftens densitet ved 0 °C (kg/m³),

      A er luftskibets areal vinkelret på bevægelsen (m²),

      c er luftskibet formfaktor og

      v er luftskibet fart (m/s).

   Der gælder, at motorens effekt (P_m) er lig med motorens kraft (F_m) gange luftskibets hastighed, dvs. for motorens krft gælder: F_m = P_m/v

   Man har nu samlet følgende formel til bestemmelse af luftskibets fart: F_l = F_m ⇒

   0,5·ρ_l·A·c·v² = P_m/v

   Dette løses med hensyn til farten v i Ti-Nspire:

   solve(0.5*1.293*kg*meter^-3*310*meter²*0.078*v²=18*10³*watt/v,v)|watt=kg*meter²*sek^-3 and meter=10^-3*km and sek=(1/3600)*time ▸ v=37.7327*km/time or kg/time³=0 (Benyttede omskrivninger: W = kg·m²·s^-3, m = 10^-3 km og s = (1/3600) t.)

   Man anslår dermed luftskibets fart til 37,7327 km/t = 38 km/t

Svar på opgave 5: Rappelling

1. Den højeste fart opnås, når accelerationen (a(t)) er nul, idet denne skifter fra positiv til negativ. Man skal derfor starte med at løse ligningen a(t) = 0 eller h''(t) = 0 med hensyn til t.

   Her er h''(t) den anden-afledede af h(t), som er højdefunktionen (eller stedfunktionen målt i forhold til jordoverfladen).

   Man kan finde h(t) som forskriften for regressionskurven til en afbildning af højde som funktion af tid.

   Man opretter lister med tid og højde i Ti-Nspire:

   tid:={0.,0.23,0.5,0.76,1.03,1.3,1.57,1.83} ▸ {0.,0.23,0.5,0.76,1.03,1.3,1.57,1.83}

   højde:={28.42,28.55,28.54,28.39,28.11,27.79,27.36,27.09} ▸ {28.42,28.55,28.54,28.39,28.11,27.79,27.36,27.09}

   Man afbilder højde som funktion af tid.

   

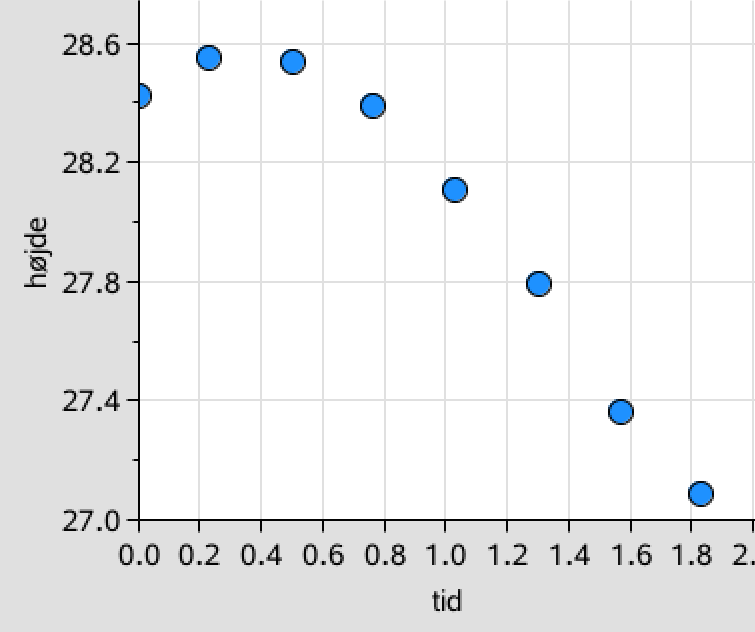
   Det ses, at starten af kurven minder om en parabel, dvs. et andengradspolynomium. Dog begynder kurven at bue den modsatte vej til sidst, så det virker nærliggende at tilnærme den med et tredjegrads-polynomium. Dette gøres i Ti-Nspire:

   CubicReg tid,højde,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Tredjegradsregression"]
   ["RegEqn","a*x^3+b*x^2+c*x+d"]
   ["a",0.391238]
   ["b",−1.66241]
   ["c",1.00076]
   ["d",28.4128]
   ["R²",0.998746]["Resid","{...}"]]

   Regressions-kurven tegnes ind i den foregående graf og det ser som vist nedenfor ud til, at kurven passer med punkterne.

   

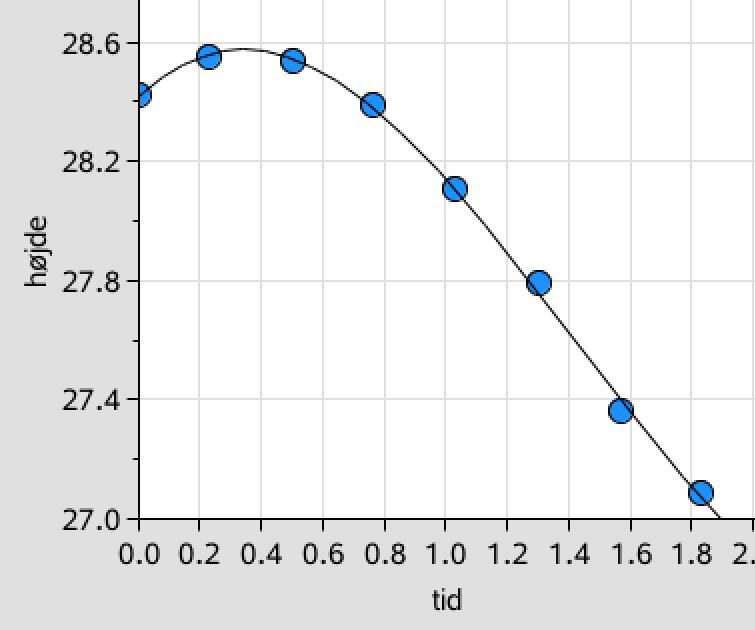
   Regressionskurvens forskrift er:

   h(t) = 0,391238·t³ - 1,66241·t² + 1,00076·t + 28,4128, (t måles i s og h(t) i m/s)

   Man får, at h''(t) = 2,34743·t - 3,32482, hvilket giver, at

   h''(t) = 0 ⇒ 2,34743·t - 3,32482 = 0 ⇔ t = 1,41637 s.

   Farten til dette tidspunkt er lig med h'(1,41637 s), hvor h'(t) = 1,17371·t² - 3,32482·t + 1,00076. Ved at indsætte t = 1,41637 s, så får man:

   h'(1,41637) = 1,17371·1,41637² - 3,32482·1,41637 + 1,00076 = −1,35383.

   Dvs. bjergbestigerens største fart er 1,35 m/s

   (Minustegnet i beregningen viser, at den opstår på vej nedad.)

2. Nendenfor er pilene for kræfterne vist:

   

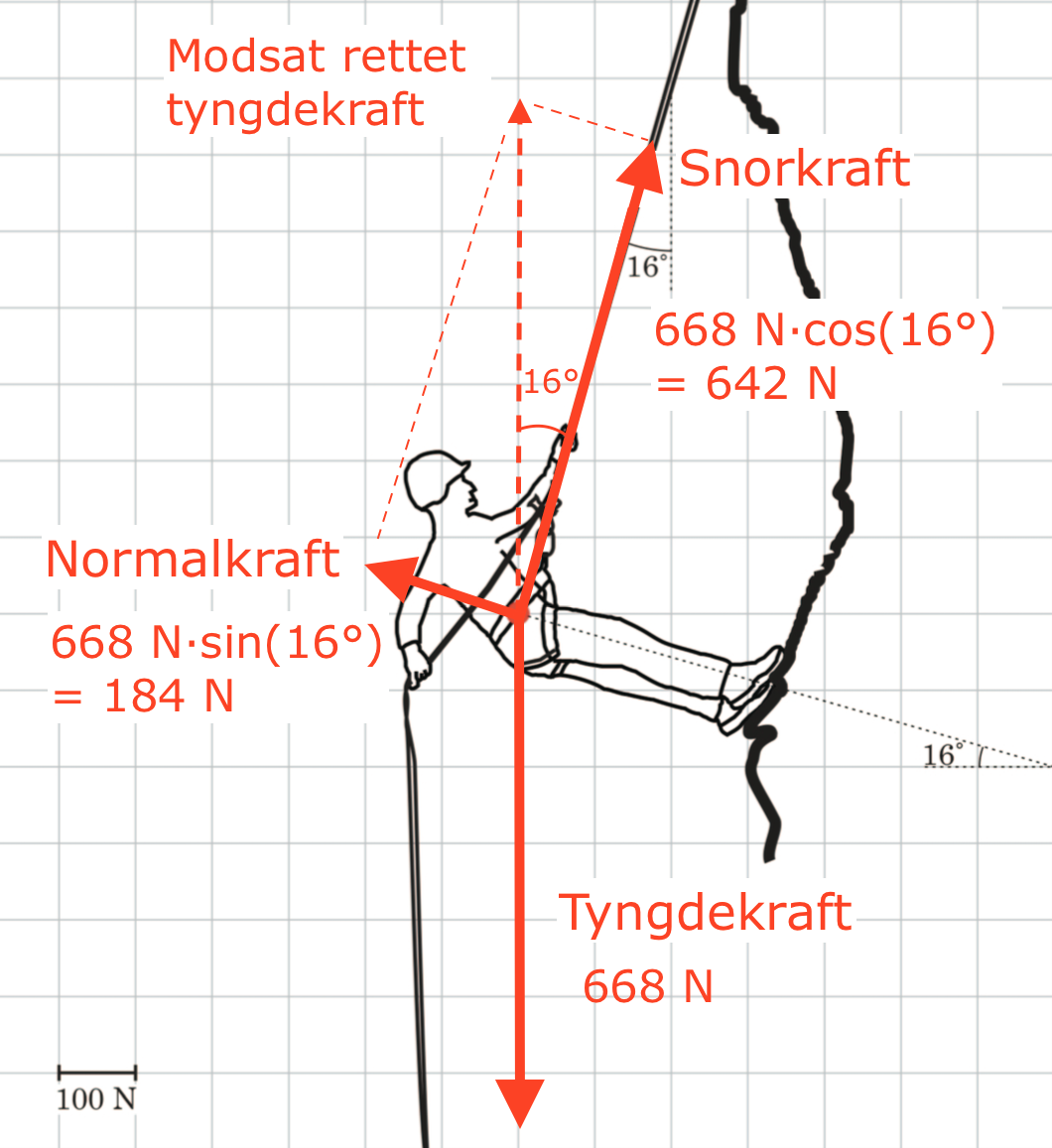
   Konstruktion: Man starter med at finde den resulterende kraft. Denne er nul, fordi personen ikke accelererer. Dernæst tegner man tyngdekraften, som er rettet nedad.

   Tyngdekraft = masse·tyngdeacceleration = (68 kg)·(9,82 m·s^-2) = 667,8 N

   Tyngdekaften skal nu ophæves af en modsatrettet kraft, der har samme størrelse som tyngdekraften for, at den resulterende kraft skal give nul. Denne hjælpekraft tegnes som en pil med stiplet linje.

   Denne modsatrettede tyngdekraft skal opløses i snorkraften, der er parallel med rebet og normalkraften, som er vinkelret på underlaget.

   Som vist på tegningen finder man:

   Snorkraft = 667,8·cos(16°) = 641,9 N

   Normalkraft = 667,8·sin(16°) = 184,1 N

Svar på opgave 6: Papirbehandling

1. For en ladning (kaldet Q og målt i C) i et elektrisk felt gælder formlen:

   Q = F·d/U, hvor

      F er kraften på ladningen i N,

      U er spændingsforkellen i feltet i V og

      d er afstanden mellem elektroderne, der skaber feltet, i m.

   Dvs. Q = (4.42·10^-9 N)·(0,24 m)/(100·10³ V) = 1,0608·10^-14 C = 1,06·10^-14 C

2. Ændringen i kinetisk energi er for latex-partiklen er 0,5·m·(v² - v₀²), hvor

      m er latex-partiklens masse,

      v₀ er partiklens fart til at starte med og

      v er partiklens fart når den rammer papiret.

   Denne ændringen er desuden lig med Q·U.

   Der gælder endelig for en kugleformet partikel: m = (4·π/3)·r³·ρ, hvor

      r er latex-partiklens radius i m³ og

      ρ er latex-partiklens densitet.

   Samlet skal man løse følgende ligning med hensyn til v: 0,5·(4·π/3)·r³·ρ·(v²-v₀²) = Q·U.

   Dette gøre i Ti-Nspire:

   solve(0.5*(4·π/3)*r³*ρ*(v²-v_0²)=q*u,v)|r=16*10^-6 meter and ρ=2.7·10³ kg/meter³ and v_0=7.5*meter/sek and q=1.0608*10^-14*coulomb and u=(100/2)*10³*volt and coulomb=kg*meter²*sek^-2*volt^-1 ▸ v=8.89659*meter/sek or v=−8.89659*meter/sek

   Dvs. latex-partiklens fart, når den rammer papiret er 8,89659 m/s = 8,90 m/s

   (Som det ses i solve-udtrykket, så bruges omskrivningen: C = kg·m²·s^-2·V^-1)

Svar på opgave 7: Produktion af K^- mesoner

1. Middellevetiden for K^- partiklen er middellevetiden i hvile gange gammafaktoren.

   Middellevetiden i hvile slås op til 1,2·10⁻⁸ s.

   Dvs. middellevetiden for K^- partiklen er 1,88·10⁻⁸ s

2. Kvarksammensætning:

   Før reaktion: π^-: dū og p: uud. Sammenlagt (idet en kvark går ud mod sin antikvark): ddu

   Efter reaktion: K^-: sū, K⁺: us̅ og n: ddu. Sammenlagt: ddu.

   Kvarksammensætningen er samlet set ddu både før og efter reaktionen.

   Bevis:

   Det ses, at flavour er bevaret for reaktionen, dvs der er tale om stærk vekselvirkning. Tilsættes mere energi vil, der dannes tungere partikler, men vekselvirkningen og dermed kvarksammensætningen vil være det samme.

   Da det forudsættes, at der dannes K^- kan der derfor ikke dannes andet end K⁺ og n for, at kvarksammensætning er bevaret.

3. Den kinetiske energi en partikel skal have i et sammenstød for at reagere med en partikel, der er i hvile kaldes tærskelværdien. Der gælder følgende formel for denne:

   Tærskelværdi for kinetisk energi = [(m_efter)² - (m_før)²]·c²/(2·m_target), hvor

      m_før er massen af partikler før reaktionen,

      m_efter er massen af partikler efter reaktionen og

      m_target er den partikel, som er i hvile (her protonen). Man får

   Masse før: (139,6 + 938,3) MeV/c² = 1077,9 MeV/c².

   Masse efter: (2·493,7 + 939,6) MeV/c² = 1927,0 MeV/c².

   M_target = 938,3 MeV/c².

   Tærskelværdi for kinetisk energi =

      [(1927,0 MeV/c²)² - (1077,9 MeV/c²)²]·c²/(2·938,3 MeV/c²) =

      [3,71333 - 1,16187]·10⁶/1876,6 MeV =

      1360 MeV.

   Pionens energi består af dens kinetisk energi plus dens masse gange lysets hastighed i anden. Man får:

   Pionens kinetisk energi = 1500 MeV - 139,6 MeV = 1360 MeV.

   Det ses, at pionens kinetiske energi er lig med tærskelværdien for reaktionen, og at dens energi derfor netop er tilstrækkelig til at producere K^- mesoner.