Svar på opgave 1: Springvand med solceller

1. Ladningen (Q) følger formlen:

   Q = E/U, hvor

      E er den afgivne elektriske energi i J og

      U er spændingen i V. Man får:

   Q = (70 kJ)/(6,0 V) = 12 kC

2. Det antages, at batteriet ikke modtager energi, når det er overskyet.

   Springvandets pumpe tilføres en energi på 70 kJ pr. time. Heraf føres 15% videre til springvandet og bruges til at løfte 300 L vand til en højde af 0,8 m pr. time.

   Den energi, som dette kræver, er den potentielle energi af vandet:

   E_pot = ρ_vand·V_vand·g·h, hvor

      ρ_vand er vandets densitet i kg·m^-3,

      V_vand er vandets volumen i m³ pr. time,

      g er tyngdeaccelerationen i m·s^-2 og

      h er springvandets højde.

   Densiteten af vand sættes til 1,00 kg/L ved 20 °C.

   Den tid, som det tager at aflade batteriet, kaldes ∆t.

   ∆t = (70 kJ)·(15 %)/((300 L/time)·(1,00 kg/L)·(0,8 m)·(9,82 m/s)) =

   (70·10³ kg·m²·s^-2)·(15 %)/((300·(0,1 m)³/(3600 s))·(1,00 kg/(0,1 m)³)·(0,8 m)·(9,82 m/s²)) =

   16038,7 s. Dette omregnes til timer: (16038,7/3600) t = 4,5 t.

   Dvs. springvandet kan fungere i 4,5 t, når det er overskyet.

Svar på opgave 2: Marie Curies notesbøger

1. Henfaldet af Ra-226 til Tl-210 følger henfaldskæden i uran-familien (Databog s. 217), hvor

      ⇒ angiver alfa henfald,

      → angiver beta-minus henfald. Man får:

   

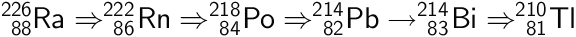
   Tl-210 henfalder til Pb-210 ved beta-minus henfald. Reaktionsskemaet er:

   

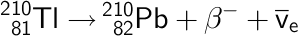
2. Formlen for aktiviteten (A(t)) som funktion af tiden af et radioaktivt stof er:

   A(t) = A₀·(0,5)^t/T, hvor

      A₀ er startaktiviteten i Bq (= s^-1),

      T er isotopens halveringstid i år og

      t er tiden i år siden det valgte starttidspunkt, som her er 1898.

   Halveringstiden for Ra-226 er 1600 år. Dette regnes om til sekunder, idet der regnes med 365,25 dage på et år: 1600 år = 1600·365,25·24·3600 s = 5,0492·10¹⁰ s.

   Der gælder formlen: m₀ = A₀·ln(2)^-1·T·m_n, hvor m_n er massen af en enkelt kerne af isotopen i kg.

   Man beregner først A₀, aktiviteten af Radium i 1898.

   Man ved, at A(2005 - 1898 år) = A(107 år) = 2800 Bq. Dette giver for A₀: 2800 Bq = A₀·0,5^107/1600 ⇒ A₀ = 2932,9 Bq.

   Man slår m_n op til (226,025 u)·(1,66·10^-27 kg/u) = 3,7520·10⁻²⁵ kg.

   Tallene indsættes i formlen m₀ = A₀·ln(2)^-1·T·m_n og man får:

   m₀ = (2932,9 s^-1)·ln(2)^-1·(5,0492·10¹⁰ s)·(3,7520·10⁻²⁵ kg) = 8,0159·10^-11 kg

   Dvs. den oprindelige masse af Radium anslås til 8,02·10^-11 kg

Svar på opgave 3: Blyhagl

1. Massen (m) af 5,0 L flydende bly har formlen:

   m = ρ_bly·V_bly,

      ρ_bly er densiteten af flydende bly og

      V_bly er rumfanget af flydende bly.

   Dvs. massen af flydende bly er (10,21·10^-3 kg/cm³)·5,0·(10 cm)³ = 51,1 kg

2. Størkningsvarmen, der afgives, er (24,7·10³ J/kg)·(0,13·10^-3 kg) = 3,211 J

   Varmen, der afgives under afkølingen, er ((327 - 100) K)·(130 J/(kg·K))·(0,13·10^-3 kg) = 3,836 J

   Samlet: (3,211 + 3,836) J = 7,047 J

   Effekt = (7,047/3,05) W = 2,31 W

3. Størrelsen af den resulterende kraft er m·a, hvor m er blyhaglet masse og a er dets acceleration efter 2,5 s.

   Accelerationen aflæses som hældningen til kurven for t = 2,5 sek. Denne er som vist: (5,7 m/s)/(1,3 s) = 4,385 m/sek².

   

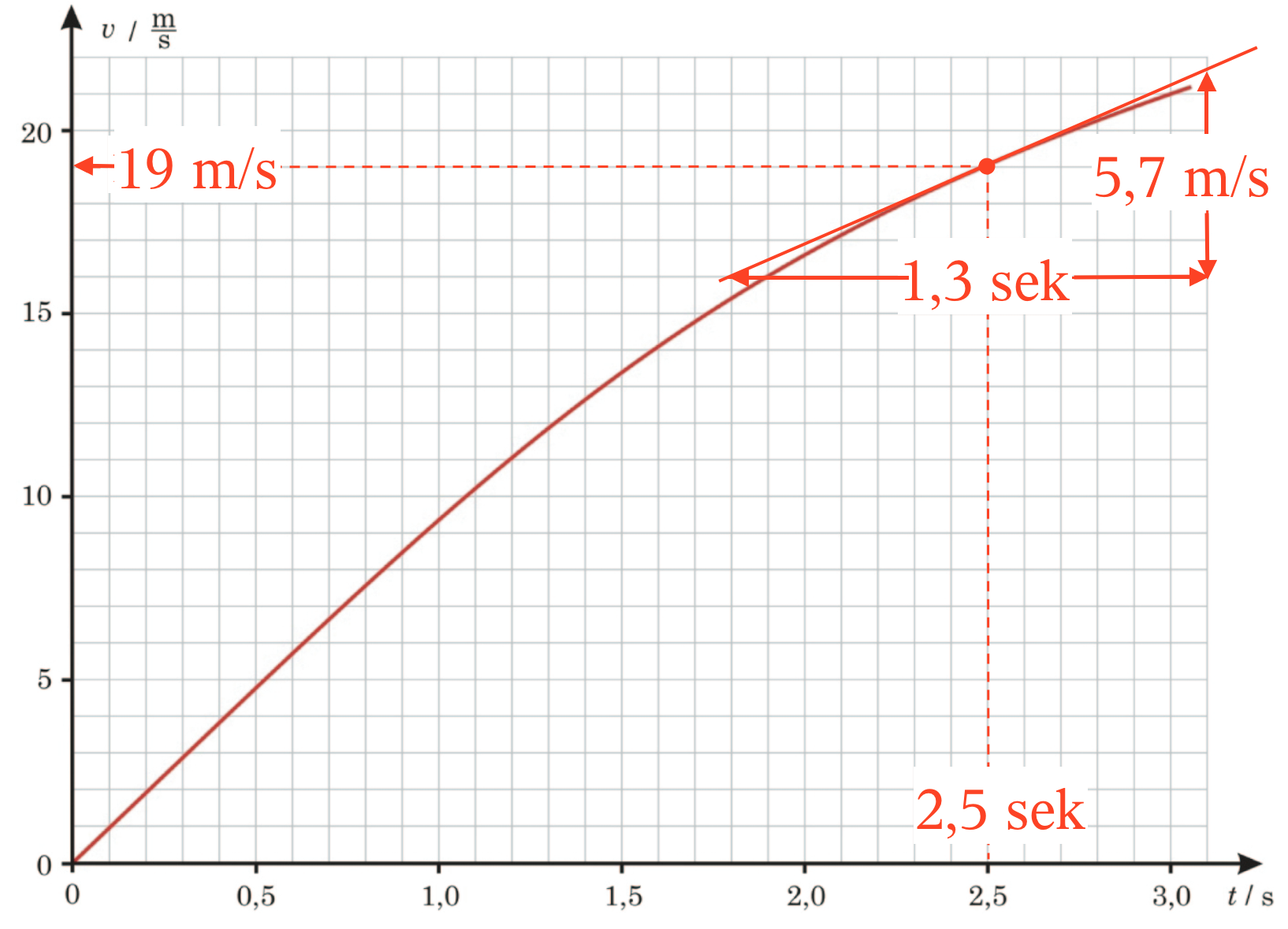
   Dermed er den resulterende kraft på et hagl efter 2,5 s: (0,13·10^-3 kg)·(4,385 m·s^-2) = 5,70·10^-4 N

   For at finde formfaktoren (c), skal man benytte, at den resulterende kraft er lig med tyngdekraften minus luftmodstandskraften.

   Formlen for luftmodstandskraften er F_luft = 0,5·ρ·c·A·v², hvor

      ρ er luftens densitet i kg·m^-3,

      A er haglets tværsnitsareal vinkelret på bevægelsesretningen i m² og

      v er haglets fart i m·s^-1

   Dette giver formlen for c:

   m·a = m·g - 0,5·ρ·c·A·v² ⇒ c = (m·g - m·a)/(0,5·ρ·A·v²)

   Farten af blyhaglet er 19 m/s efter 2,5 s som vist på figuren ovenfor.

   Densitet af luft slås op til 1,293 g/L = 1,293 kg/m³

   Tyngdekraft på hagl = (0,13·10^-3 kg)·9,82 m·s^-2 = 1,28·10^-3 N

   Tværsnitsareal af hagl vinkelret på bevægelsesretningen = π·(1,4·10^-3 m)² = 6,1575·10^-6 m²

   Indsat i formlen c = (m·g - m·a)/(0,5·ρ·A·v²) fås:

   c = (1,28·10^-3 N - 5,70·10^-4 N)/(0,5·(1,293 kg/m³)·6,1575 m²·10^-6·(19 m/s)²) = 0,49197

   Dvs. c = 0,49

Svar på opgave 4: Henfald

1. Bevægelsesmængden for partiklen er en vektor, p̅, hvis størrelse kaldes p. Ved partiklens henfald gælder bevægelsesmængdebevarelse, hvor p̅ for partiklen før henfaldet er lig med vektor-summen af p̅'erne for de partikler, som dannes.

   Hvis partiklen ligger stille inden henfaldet, så vil de dannede partikler bevæge sig væk fra hinanden med en vinkel på 180° mellem dem. Hvis partiklen derimod som her har en fart inden henfaldet, så vil vinklen mellem de dannede partikler være mindre end 180°.

   På billedet nedenunder kaldes partiklens bevægelsesmængde for p̅_før og summen af fotonerens bevægelsesmængder kaldes p̅_efter. Længden af denne vektor er lig summen af længderne af projektionerne af bevægelsesmængdevektorerne for fotonerne på en linje parallel med partiklens bevægelsesmængde-vektor.

   

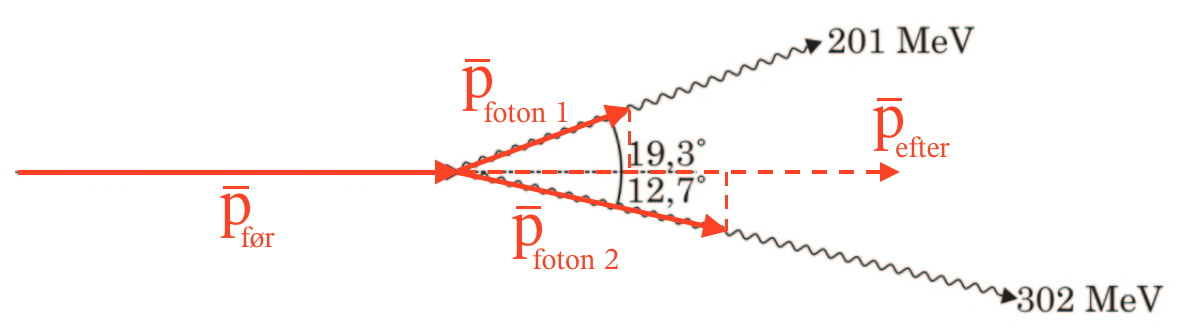
   En højenergi-partikels energi (E) følger formlen: E² = m²·c⁴ + p²·c². For fotoner gælder at m ≈ 0 og dermed er E = p·c eller p = E/c. Derfor har bevægelsesmængden for de to fotoner størrelserne: 201 MeV/c og 302 MeV/c. Her er c lig med lysets hastighed, som man dog ikke indsætter en talværdi for.

   Størrelsen af den ene fotons projektion på partiklens bevægelsesmængdevektor er (201 MeV/c)·cos(19,3°) og størrelsen af den anden er (302 MeV/c)·cos(12,7°). Tilsammen får man følgende størrelse af partiklens bevægelsesmængde:

   |p̅| = (201 MeV/c)·cos(19,3°) + (302 MeV/c)·cos(12,7°) = 484 MeV/c

2. Der gælder energibevarelse, så partiklens energi er lig med summen af fotonernes energi.

   E = 201 MeV + 302 MeV = (201 + 302) MeV = 503 MeV

   Af formlen: E² = m²·c⁴ + p²·c² fås partiklens masse: m = √[E² - (p·c)²]/c²

   Tallene for energierne indsættes: m = √[(503 MeV)² - (484 MeV)²]/c² = 136,9 MeV/c²

   Det ses af databogen side 241, at en π⁰ meson henfalder til γ + γ (to fotoner), og at den har massen 135 MeV/c². Dette passer med den ukendte partikel.

Svar på opgave 5: Massespektrograf

1. Ladningen bevæger sig med jævn cirkelbevægelse, dvs. den påvirkes af en resulterende kraft, der peger mod centrum af cirklen. Hastighedsvektoren er tangent til cirklen. Magnetfeltets kraft peger indad i tegningens plan som vist nedenunder.

   

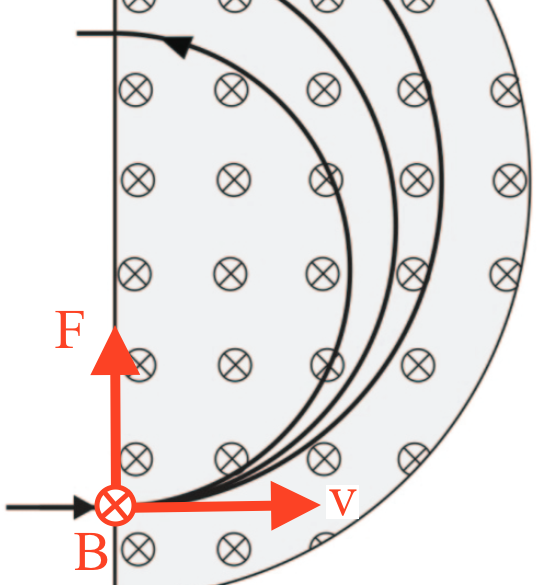
   Ladningens fortegn findes ved hjælp af højrehåndsreglen. Det antages, at man vender højre hånds tommel-, pege- og langfinger så de står vinkleret på hinanden. Der gælder, at for en positiv ladning vil hastighedsvektoren svare til højre hånds tommelfinger, magnetfeltet til højre hånds pegefinger og kraften til højre hånds langefinger.

   Da dette passer med tegningen, så er ladningen positiv

2. Man opretter masserne og radierne som lister i Ti-Nspire.

   masser:={5.012,6.015,7.016,8.022,9.027,10.035} ▸ {5.012,6.015,7.016,8.022,9.027,10.035}

   radier:={0.435,0.524,0.601,0.683,0.783,0.876} ▸ {0.435,0.524,0.601,0.683,0.783,0.876}

   Man laver en lineær regression på de to lister:

   LinRegMx masser,radier,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Lineær regression (mx+b)"]
   ["RegEqn","m*x+b"]
   ["m",0.087155]
   ["b",−0.005175]
   ["r²",0.998291]
   ["r",0.999145]
   ["Resid","{...}"]]

   Man får følgende lineære sammenhæng:

   R = (0,087155 m/u)·M - 0,005175 m, hvor

      R er radius i m som funktion af massen M i u.

   Man skal nu udlede en linær sammenhæng mellem R og M, hvor B indgår. På den måde kan man finde B ud fra de koefficienter, som man fandt i den lineære regression. Man har, når B er vinkelret på v, at den resulterende kraft på den enkelte Li-ion er:

   F_B = q·v·B.

   Denne kraft er samtidig lig med centripetalkraften i Li-ionens cirkelbevægelse, dvs. q·v·B = M·v²/R. Dette giver: R = (v/(B·q))·M.

   Hvis man sammenligner dette udtryk med resultatet af den lineære regression, så får man, at

   0,087155 m/u = v/(B·q). Dette giver: B = v/((0,087155 m/u)·q). Heri indsætter man værdierne:

   v = 2,87·10⁶ m/s,

   u = 1,661·10^-27 kg og

   q = elementarladning = 1,602·10^-19 C (Li-ionerne har een positiv ladning)

   Dvs. B = (2,87·10⁶ m/s)/((0,087155 m/(1,661·10^-27 kg))·1,602·10^-19 C) =

      0,341426 kg/(C·s) = 0,341 T

   (Benyttet omskrivning: T = kg/(C·s))

Svar på opgave 6: Roning

1. Der gælder formlen: Fart = distance/tid, hvor distancen er 2000 m og tiden i sekunder er: 6·60 s + 57,82 s = 417,82 s.

   Dvs. roerens gennemsnitsfart er: (2000 m)/(417,82 s) = 4,79 m/s

2. Man antager, at der er konstant acceleration. Der gælder

   s(t) = 0,5·a·t² og v(t) = a·t ⇒ s(t) = 0,5·v(t)²/a.

   Ved s(t) = 90 meter har man, at v(t) = 19,9·10³ m/(3600 s) = 5,5278 m/s. Dette indsættes i ovenstående ligning, og man løser den med hensyn til a:

   90 m = 0,5·(5,5278 m/s)²/a ⇒ a = 0,16976 m/s²

   Dvs. accelerationen er 0,170 m/s²

3. Energien i et håndtag er arealet under kurven. Nedenunder er dette fundet ved at tegne et polygon i Ti-Nspire som vist med blåt:

   

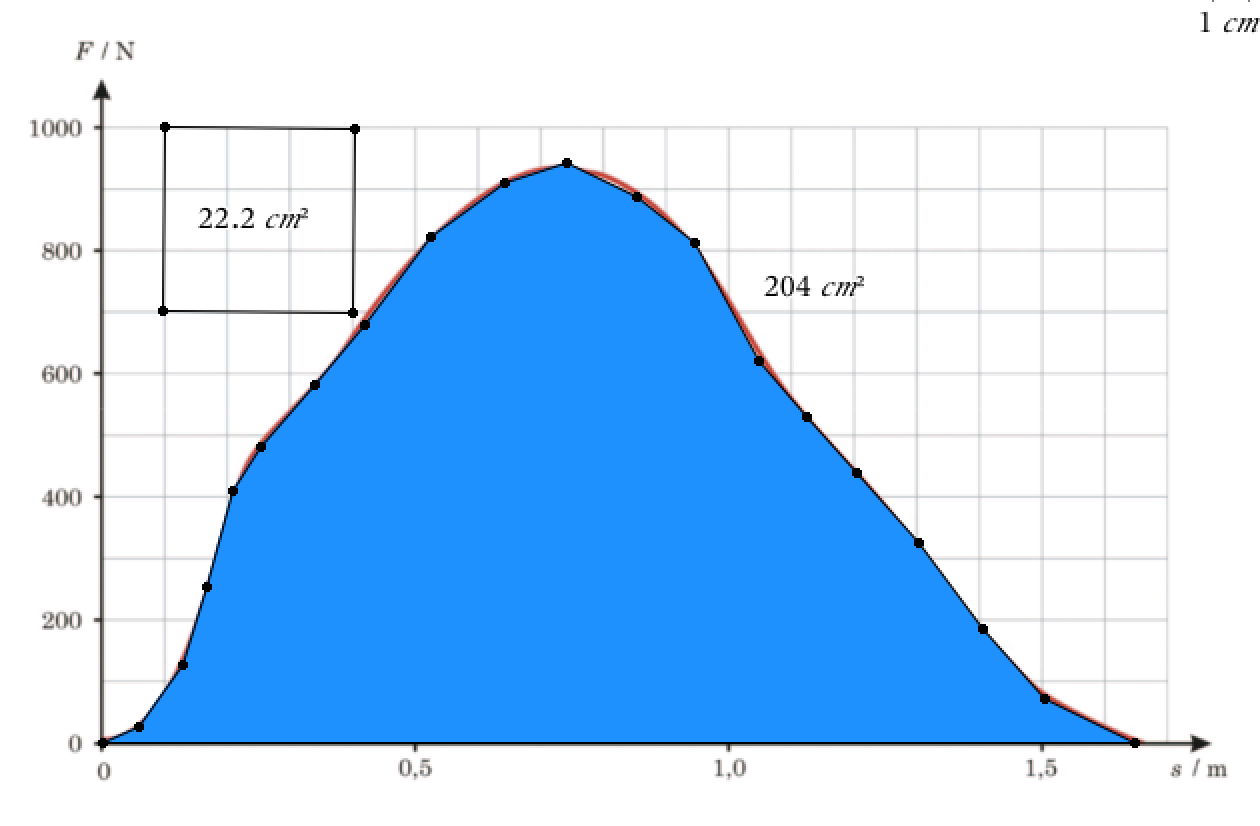
   Målestokken er valgt af Ti-Nspire og kan ikke bruges direkte. I stedet skal man beregne antallet af tern under kurven og benytte, at en tern svarer til (0,1 m)·(100 N) = 10 J.

   Arealet af 9 tern er målt til 22,2 cm², dvs. arealet af en tern er 22,2/9 cm² = 2,467 cm².

   Arealet under kurven er 204 cm².

   Antal tern: 204/2,467 = 82,70

   Dette antal tern svarer til: 82,70·10 J = 827,0 J

   Et håndtag varer (60 s)/32 = 1,875 s

   Effekten er dermed: (827,0 J)/(1,875 s) = 441 W

Svar på opgave 7: Stangtennis

1. Radius i cirkelbevægelsen er 0,90 m vurderet ud fra boldens afstand til stangen i forhold til børnenes størrelse. Det antages, at der er ikke er nogen gnidning eller luftmodstand i bevægelsen.

   Vinklen melllem snor og stang kaldes θ. Jo større fart, jo tættere er denne vinkel på 90°.

   Nedenunder er bolden vist som en cirkel til højre og stangen som en lodret streg til venstre. Vinklen θ er aflæst til 80° som vist.

   F_T er tyngdekraften, F_S er snorkraften og F_C er den resulterende kraft, centripetalkraften, der peger mod centrum af cirkelbevægelsen. F_T virker på bolden, men har en komposant, der forbinder endepunkterne af de to andre kræfter, så man får en retvinklet trekant med θ som den ene vinkel.

   

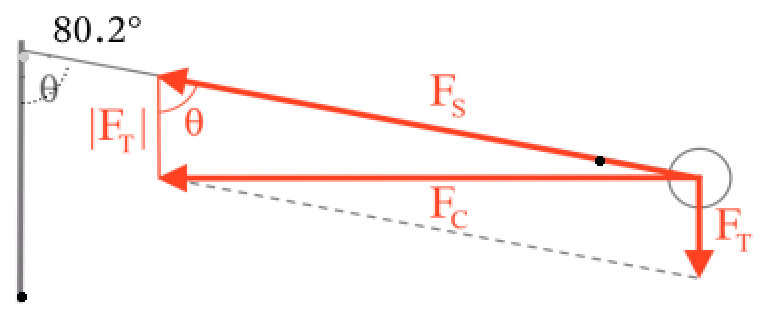
   (Figuren er lavet i et tegneprogram og vinklen er målt i Ti-Nspire.)

   Centripetalkraftens størrelse er m·v²/r. Tyngdekraftens størrelse er m·g. Der gælder:

   tan(θ) = (m·v²/r)/(m·g) ⇒ v = √[tan(θ)·g·r]. Heri indsættes: radius = 0,9 m, g = 9,82 m·s^-2 samt θ = 80° og man får...

   v = √[tan(80°)·(9,82 m·s^-2)·(0,9 m)] = 7,0797 m/s.

   Dvs. boldens fart er 7,1 m/s i situationen på billedet