Svar på opgave 1: Wolf-Rayet stjerne

1. Densiteten af stjernen er masse divideret med rumfang, hvor stjernen opfattes som kugleformet:

   (4,9·10³¹ kg)/((4/3)·π·(2,1·10⁹ m)³) = 1263 kg/m³

2. Man bruger Stefan-Boltzmans lov for den effektive temperatur af en stjerne.

   L = 4·π·R²·σ·T⁴, hvor

       L er stjernens udstråling i W,

       R er stjernens radius i m,

       σ er Stefan-Boltzmanns konstant (= 5,67·10^-8 W·m^-2·K^-4 ) og

       T er stjernens effektive temperatur i K.

   Den effektive temperatur af en stjerne er den temperatur, som et sort legeme af samme masse må have for at afgive samme effekt som stjernen. Man får T til:

   ⁴√[(4,2·10³¹ W)/(4·π·(2,1·10⁹ m)²·5,67·10^-8 W·m^-2·K^-4)] = 6,0·10⁵ K

Svar på opgave 2: Varmelegeme til akvarium

1. Man opretter lister med stømstyrker og effekter fra tabellen i Ti-Nspire:

   strømstyrke:={0.1,0.2,0.3,0.4,0.5,0.6,0.75} ▸ {0.1,0.2,0.3,0.4,0.5,0.6,0.75}

   effekt:={3.2,13.5,30.2,52.3,82.3,120,183} ▸ {3.2,13.5,30.2,52.3,82.3,120,183}

   Man opretter en ny liste for spændingen, der er effekt-listen divideret med strømstyrke-listen:

   spænding:=effekt/strømstyrke ▸ {32.,67.5,100.667,130.75,164.6,200.,244.}

   Man laver en potens-regression på effekt-listen og spændings-listen:

   PowerReg spænding,effekt,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",0.003121]
   ["b",1.99399]
   ["r²",0.999828]
   ["r",0.999914]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Dvs. sammenhængen mellem spændingsfald (U) og effekt (P) er:

   P(U) = 0,00312·U^1,99

   Effekten, der afgivet, når spændingen er 230 V findes som P(230), der giver:

   P(230) = 0,00312·230^1,99 W = 160 W

Svar på opgave 3: Segway

1. Sammenhængen mellem tilbagelagt strækning (s), forbrugt tid (t) ved konstant fart (v) er: s = t·v ⇒ t = s/v. For Segwayen får man den forbrugte tid ved maksimum fart til:

   t = (800 m)/(5,6 m/s) = 143 s

2. For at finde bremselængden, skal man have formlerne for strækning (s(t)) og og fart (v(t)) ved konstant (negativ) acceleration.

   Strækning: s(t) = 0,5·(-4,7 m/s²)·t² + (4,2 m/s)·t og

   Fart: v(t) = (-4,7 m/s²)·t + 4,2 m/s

   Bemærk at accelerationen er negativ, da der er tale om en opbremsning og da accelerationen dermed er modsatrettet bevægelsen.

   For at finde bremselængden, skal man kende den tid, som det tager at bremse. Denne findes af udtrykket for v(t), da man ved, at v(t) = 0, når opbremsningen er afsluttet. Man finder den tid (t) som opbremsningen tager:

   (-4,7 m/s²)·t + 4,2 m/s = 0 ⇒ t = 0,945 s

   Denne tid indsættes i udtrykket for strækningen og man får bremselængden til:

   0,5·(−4,7 m/s²)·(0,945 s)² + (4,2 m/s)·(0,945 m/s) = 1,87 m

3. Den resulterende kraft på person+Segway er 0 eftersom Segwayen kører med konstant fart.

   Tyngdekraften (F_t) + normalkraft (F_n) + gnidningskraft (F_g) som vektorer skal derfor give summen 0.

   Tyngdekraftens størrelse er (9,82 m/s²)·(145 kg) = 1424 N

   Normalkraftens størrelse er 1424·cos(8°) N = 1410 N

   Tyngdekraftens komposant parallelt med underlaget (F_tu) er 1424·sin(8°) = 198 N.

   Motorkraftens størrelse (F_m) er F_g + F_tu = 130 N + 198 N = 332 N.

   Disse krafter er tegnet ind på figuren nedenunder (F_t, F_n og F_tu er blå; F_g er rød og motorkraften er sort)

   

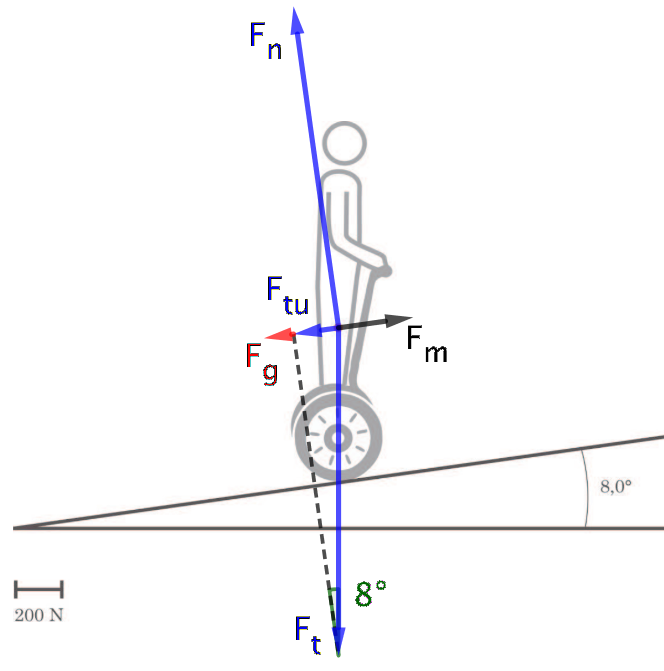
   Uden for opgaven: Der virker også et drejningsmoment på Segwayen. Hjulene påvirker underlaget med en kraft, der er lig med motorkraften. Dette giver et drejningsmoment, der virker tilbage på styret, og som afbalanceres ved, at personen læner sig forover. Begge kræfter og deres arme er vist med rødt på nedenstående figur.

   

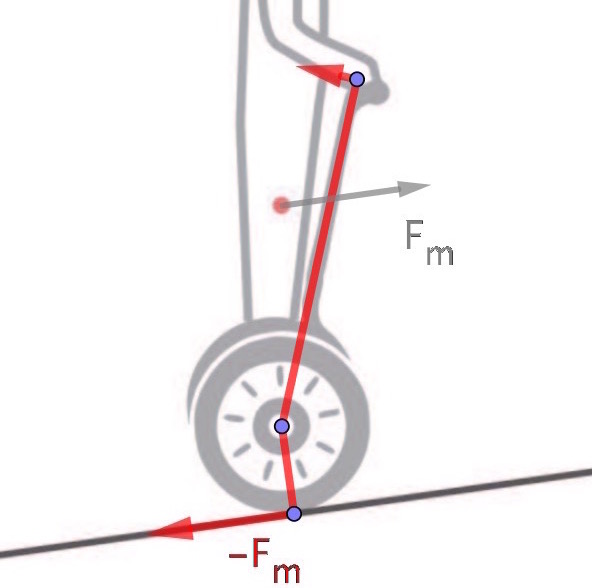
Svar på opgave 4: Teegardens stjerne

1. Det antal grader som stjernen bevæger sig hen over himlen set fra jorden findes ved hjælp af Pythagoras læresætning.

   

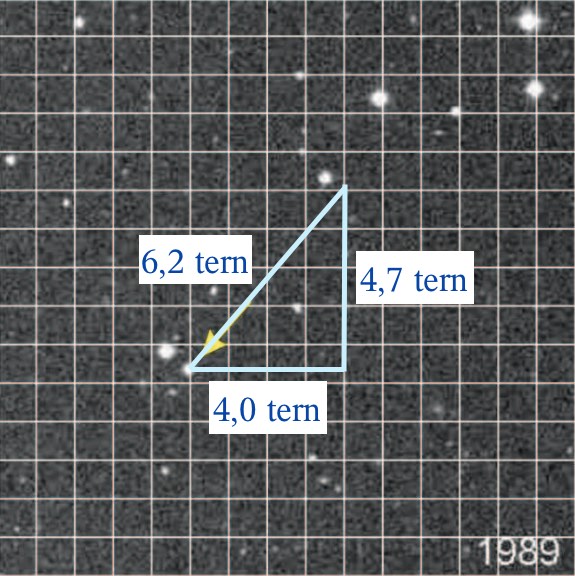
   Som det ses bevæger stjernen sig 4 tern ned og 4,7 tern til venstre. Dette svarer til √[4² + 4,7²] = 6,2 tern i lige linje.

   6,2 tern svarer til 0,01°·6,2 = 0,062°. Dvs. set fra jorden bevæger stjernen sig langs en cirkelbue, der er 0,062°. I virkeligheden må det antages, at den bevæger sig langs en ret linje, der går fra start til slutpunkt, men da vinklen er lille kan man antage buen og linjestykket for at være lige lange.

   Buens længde og dermed stjernens vandring er 2·π·(1,19·10¹⁷ m)·(0,062°/360°) m = 1,288·10¹⁴ m

   Denne strækning skal divideres med tiden i sekunder, som er (1989-1951)·365,15·24·3600 s = 1,199·10⁹ s.

   Dvs. stjernens fart er (1,288·10¹⁴ m)/(1,199·10⁹ s) = 1,1·10⁵ m/s

2. Man bruger afstands-kvadratloven for at finde den energi, som teleskopet modtager pr sekund:

   0,79·(3,8·10²¹)/(4·π·(1,19·10¹⁷)²) W = 1,687·10^-14 W

   Dvs. den samlede energi på 8 timer bliver: (1,687·10^-14 W)·(8·3600 s) = 4,9·10^-10 J (eller 0,49 nJ)

Svar på opgave 5: Fødevarebestråling

1. Co-60 henfalder ved beta-minus henfald (i følge tabelopslag):

   

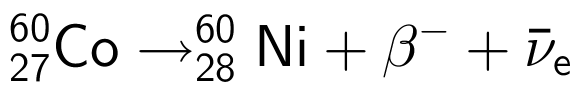
2. Man skal finde P(t), der er effekten til tiden t = 0. Man har:

   P(0) = Q·k·m(Co)/M(Co), hvor

       Q = 4,01·10¹³ J = energien pr. henfald

       k er hastighedskonstanten for henfaldet i s^-1

       m(Co) = 0,707 kg er massen af alle Co-60 kernerne i kg og

       M(Co) er massen af én Co-60 kerne i kg

   k = ln(2)/T_0,5, hvor T_0,5 er halveringstiden for henfaldet. Denne slås op til 5,272 år. Målt i sekunder er T_0,5 = 5,272 år = 5,272·365,25·24·3600 sek = 1,6637·10⁸ s. Det giver for k:

   k = ln(2)/(1,6637·10⁸ s) = 4,166·10⁻⁹/s

   m(Co)/M(Co) = (0,707 kg)/((59,93 u)·(1,661·10^-27 kg·u^-1)) = 7,102·10²⁴ stk.

   P(0) = (4,01·10^-13 J)·(4.166·10^-9/s)·7,102·10²⁴ = 1,187·10⁴ J/s = 11,9 kW

Svar på opgave 6: Titan og Cassini-Huygens

1. Radius (r) af Titan kan beregnes ved hjælp af formlerne for massetiltrækning i rummet og tyngdekraft ved overfladen.

   Der gælder: F = G·M·m/r² = m·g, hvor

       F er kraften på et legeme, der er under påvirkning af Titans tyngdefelt,

       G er gravitationskonstanten,

       M er Titans masse og

       g er Titans tyngdeacceleration ved overfladen.

   Dette giver r = √[G·M/g] =

   √[(6,67·10⁻¹¹ N·m² kg^-2·1,34·10²³ kg)/(1,35 m·s^-2)] = 2,57·10⁶ m

2. Atmosfærens densitet ved overfladen af Titan kan findes ud fra formlen for luftmodstand af faldskærmen:

   F_l = 0,5·c_w·ρ·A·v², hvor

       F_l er faldskærmens luftmodstand i N,

       c_w er faldskærmens formfaktor (enhedsløs),

       ρ atmosfærens densitet i kg·m^-3,

       A er faldskærmens areal på tværs af bevægelsesretningen i m² og

       v er faldskærmens fart i den nederste del af Titans atmosfære målt i m·s^-1.

   I denne formel isoleres ρ:

   ρ = 2·F_l/(c_w·A·v²)

   Man finder v: De nederste ca. 2 km af Titans atmosfære nærmer kurven sig en ret linje, hvor linjens hældning er terminalfarten, dvs. den konstante fart som faldskærm og sonden bevæger sig med efter opbremsningen i atmosfæren. Linjen er vist med blåt på figuren nedenunder.

   

   Dvs. v = den numeriske værdi af linjens hældning = (27000 m)/(6300 s) = 4,29 m/s.

   Man finder F_l: Da rumsonden tilnærmelsesvis har nået sin slutfart ved overfladen, dvs. ikke længere accelererer, er der ikke nogen resulterende kraft på den, og luftmodstanden og tyngdekraften ophæver dermed hinanden. Dette giver:

   Luftmodstand = tyngdekraft ⇒ F_l = m·g, hvor m er massen af rumsonden og g er tyngdeacceleration ved Titans overflade.

   Desuden gælder, at A = π·r², hvor r er faldskærmens radius.

   Man får den samlede formel for atmosfærens densitet: ρ = 2·g·m/(c_w·π·r²·v²), dvs.:

   ρ = 2·(1,35 m·s^-2)·(239 kg)/(0,89·π·(1,51 m)²·(4,29 m·s^-1)²) = 5,50 kg·m^-3

   Kontrol: Ved tabelopslag finder man, at Titans atmosfære består af næsten 100 % N₂ (med molmassen 0,028 kg·mol^-1), har et tryk på 146,7 kPa og en temperatur på 97 K. Ved hjælp af idealgasligningen får man følgende værdi af atmosfærens densitet:

   ρ = (146700 N·m⁻²)·(0,028 kg·mol^-1)/((8,314 J·mol⁻¹·K⁻¹)·(93 K)) = 5,3 kg·m^-3

Svar på opgave 7: Kraftig laser

1. Laserens effekt (P) er dens udsendte energi divideret med tidsrummet, som energien udsendes i. Man får:

   P = (1,2·10⁶ J)/(2,9·10^-9 s) = 4,1·10¹⁴ W (eller 0,41 PW)

2. Man skal bruge formlen for varmeenergi:

   Q = C·ΔT ⇒ ΔT = Q/C, hvor

       Q er den energi, der tilføres pillen, i J,

       C er pillens varmekapacitet i J·K^-1 og

       ΔT er ændringen i temperatur i K.

   Man får følgende ændringen i pillens temperatur (så længe pillen er på fast form):

   ΔT = (1,2·10⁶ J)/(0,025 J/K) = 4,8·10⁷ K (eller 48 MK. Dette virker ulogisk, da pillen vil være fordampet længe inden denne temperatur nås.)

3. Hvis fotoner (som her) absorberes vil der gælde: F = p/Δt, hvorimod der ved reflektion af lys gælder: F = 2·p/Δt. Her er

       F er fotonens kraft i N,

       p er fotonens bevægelsesmængde i N·s og

       Δt er den tid som kraften virker i målt i s.

   For en foton er p = E/c, hvor

       E er fotonens energi i J og

       c er lysets hastighes i m·s^-1.

   En fotons tryk = F/A = (p/Δt)/A = E/(c·Δt·A), hvor A er pillens overfladeareal.

   For trykket af alle fotoner i laserstrålen gælder samme formel, idet E nu står for alle fotonernes energi.

   Dvs. laserens tryk på pillen er: (1,2·10⁶ Nm)/((3·10⁸ ms^-1)·(2,9·10^-9 s)·(1,2·10^-5 m²)) =

   1,15·10¹¹ N·m^-2 (eller 115 GPa. Bemærk at laserens bølgelængde ikke behøves.)