Svar på opgave 1: Nissan Leaf

1. Formlen for elektrisk effekt er P = U·I, hvor

      P er effekt i W,

      U er spænding i V og

      I er strømstyrke i A.

   Man indsætter værdierne og løser med hensyn til I:

   solve(50000=400*i,i) ▸ i=125

   Dvs. strømstyrken i ladekablet er 125 A

2. Nyttevirkning (η) = udført energi divideret med tilført energi, der giver:

   (19000·3600 J)/(50000·30·60 J) = 0,76.

   Dvs. η = 0,76

3. Luftmodstanden, kaldet F, antages at følge formlen F = 0,5·ρ·A·c·v², hvor

      ρ = 1,293 kg/m³ er luftens densitet,

      a = 2,27 m² er arealet på tværs af bevægelsesretningen i m²,

      c er formfaktoren, som er dimensionsløs og

      v er farten af bilen i m/s.

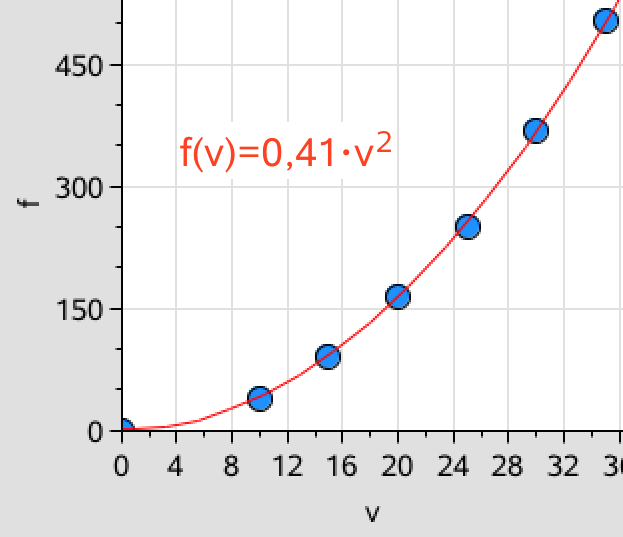
   Man skal undersøge, om der gælder en sammenhæng af formen: F = K·v² for tabellens tal, og hvilken værdi af K, der passer bedst til tallene. Formfaktoren vil kunne findes af sammenhængen: K = 0,5·ρ·A·c.

   Man opretter lister over tabellens tal for F og v og laver en andengrads-polynomie regression på listerne.

   f:={0,39,91,164,251,367,503} ▸ {0,39,91,164,251,367,503}

   v:={0,10,15,20,25,30,35} ▸ {0,10,15,20,25,30,35}

   QuadReg v,f,1: CopyVar stat.RegEqn,f2: stat.results ▸
   [["Titel","Andengradsregression"]
   ["RegEqn","a*x^2+b*x+c"]
   ["a",0.417229]
   ["b",−0.274026]
   ["c",0.30303]
   ["R²",0.999909]
   ["Resid","{...}"]]

   Regressions-formlen er: F(v) = 0,417·v² - 0,274·v + 0,303. Ud fra dette finder man ved kurvetilpasning, at F(v) = 0,41·v² er den funktion, der passer bedst (den røde kurve i diagrammet).

   

   Enheden for K er N/(m·s^-1)² = N·m^-2·s², da enheden for K·v² skal give N, der er enheden for F. Formfaktoren beregnes:

   solve(0.41*new*met^-2*sek²=0.5*(1.293*kg/met³)*2.27*met²*c,c)|new=kg*met*sek^-2 ▸ c=0.279376

   Dvs. formfaktoren er 0,28

   Bemærkning om regression: CAS kan ikke lave en potens-regression, der starter med punktet (0,0). Hvis man udelader (0,0), får man potensfunktionen F(v) = 0,37·v^2,03. Herudfra kan man igen finde det bedste funktion på formen F(v) = K·v² ved kurvetilpasning.

Svar på opgave 2: Skybrud

1. Trykket er lig med tyngden af vandsøjlen over dækslet gange dækslets areal. Tyngden er højden af vandsøjlen gange dens densitet gange dækslets areal.

   Dvs. vandets kraft på dækslet er: (37,5 m)·(9,82 m·s²)·(1000 kg/m³)·π·(0,29 m)² = 9,7·10⁴ N

Svar på opgave 3: Datering af jordlag

1. Forskellen i alder på de to jordlag kaldes x. Til tiden 0 var aktiviteten af Pb-210 i det nedre jordlag 22,9 Bq. Til tiden x er den 2,1 Bq. Man finder nu x ved hjælp af formlen for aktivitet:

   A(x) = A(0)·2^-x/T, hvor

      A(x) = 22,9 Bq,

      A(0) = 2,1 Bq og

      T = 22,6 år er halveringstiden for bly-210.

   Dette løses med hensyn til x: solve(2.1=22.9*2^{-x/(22.6*år)},x) ▸ x=77.8996*år

   Dvs. aldersforskellen mellem jordlagene er 78 år

2. Man skal finde ud af, hvor mange kerner af Pb-210, der var i prøven fra starten og derefter dividere dette med massen i kg af en kerne.

   Man har formlen antallet af kerner efter 30 døgn, N(30d):

   N(30d) = N(0)·2^-x/T, hvor man skal finde N(0) (resten er det samme som før).

   Man kender: N(0) - N(30d) = 672 som medfører, at N(30d) = N(0) - 672. Dette giver:

   N(0) - 672 = N(0)·2^-x/T ⇒ 672 = N(0)·(1 - 2^-x/T), som løses med hensyn til N(0):

   solve(672=n0*(1-2^{(−3.*d)/(22.6*365.25*d)}),n0) ▸ n0=2.66794*10⁶

   Massen af en Pb-210 kerne er 209,98 u og en u er 1,661·10^-27 kg. Man får dermed massen af alle 2,6679·10⁶ Pb-210 kerner:

   (2,6679·10⁶)·(209,98 u)·(1,661·10^-27 kg/u) = 9,305·10^-19 kg

Svar på opgave 4: 100 meter løb

1. Gennemsnitsfarten for rekordløbet på 100 meter for kvinder er tilbagelagt distance divideret med forbrugt tid: (100 m)/(10,49 s) = 9,53 m·s^-1

2. Den største vandrette kraft svarer til den største vandrette acceleration i følge Newtons anden lov, og den aflæses til 810 N som vist nedenunder med den blå pil.

   

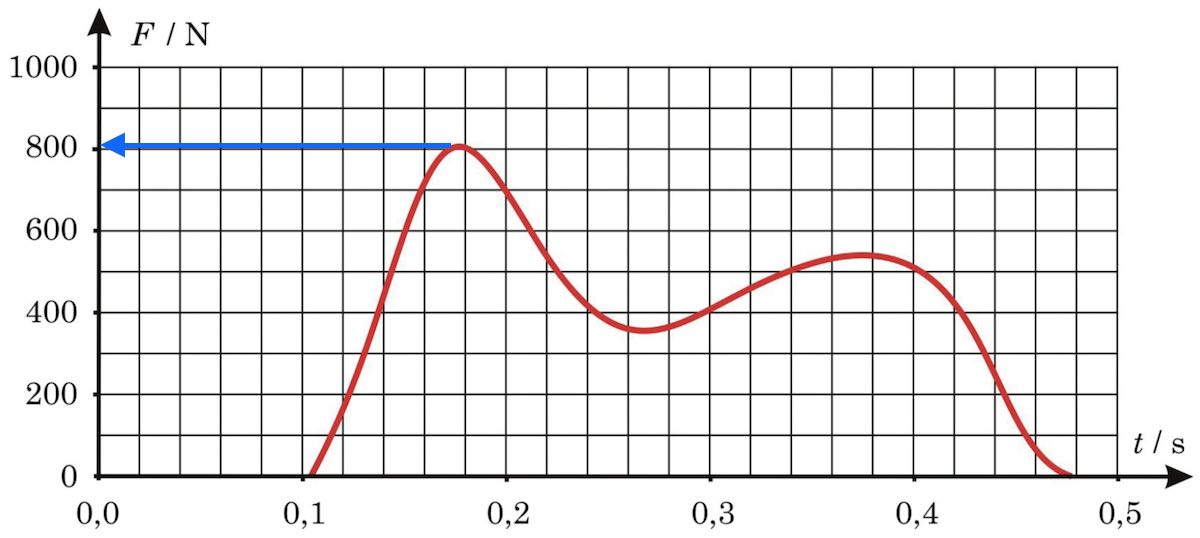
   Dvs. accelerationen er: (810 kg·m·s^-2)/(62 kg) = 13,06 m·s^-2 = 13 m·s^-2

3. Fartændringen i løbet af afsættet er lig med integralet af accelerationen som funktion af tiden. Da løberens starter i hvile, så vil integralet af accelereationen også være lig med den vandrette fart, når løberen forlader blokken.

   Integralet af accelerationen er arealet under kurven divideret med massen af løberen. (Man kan også se arealet under kurven som ændringen i bevægelsesmængde, som derefter divideres med løberens masse for at finde fartændringen.)

   

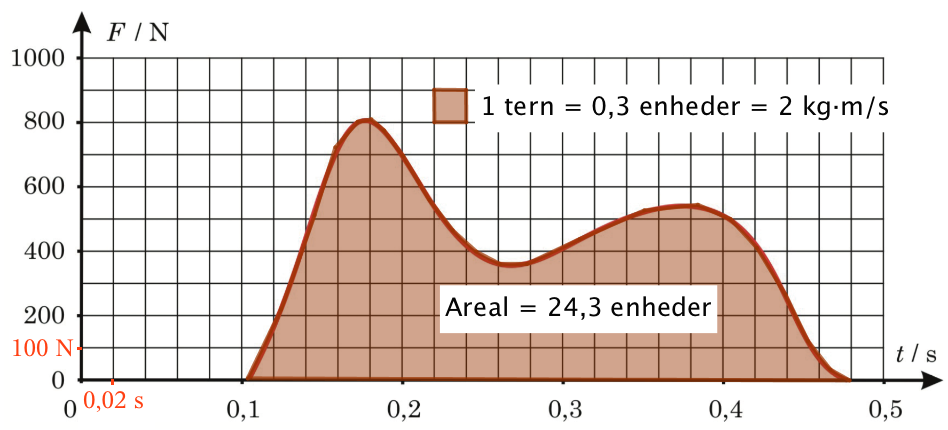
   Arealet under kurven måles som vist ovenfor i Geogebra til 24,3 enheder. En tern svarer til 0,3 enheder. Dvs. arealet i tern er (24,3 enheder)/(0,3 enheder pr. tern) = 81 tern.

   En tern svarer på grafen til: (100 N)·(0,02 s) = 2,00 N·s = 2,00 kg·m·s^-1. Dvs. arealet under kurven er (81·2,00 kg·m)/(62 kg·s) = 2,6129 m/s.

   Løberens fart efter afsættet bliver dermed 2,6 m/s

Svar på opgave 5: Rumsonden Messenger

1. Den kinetiske energi (E_k) findes ved formlen: E_k = 0,5·m·v², hvor

      m er massen af rumsonden i kg og

      v er rumsondens fart i m/s.

   E_k = 0,5·(512 kg)·(3,81·10³ m·s^-1)² = 3,716·10⁹ kg·m²·s^-2 = 3,72 GJ

2. Kraften (F), der virker på rumsonden, findes ved hjælp af tyngdekraftsformlen:

   F = G·M·m/r², hvor

      G er gravitationskonstanten = 6,67·10^-11 N·m²·kg^-2

      M er Merkurs masse i kg,

      m er rumsondens masse i kg og

      r er afstanden mellem Merkurs massemidtpunkt og rumsondens massemidtpunkt.

   Merkurs radius er 2439 km = 2,439·10⁶ m. Dette skal lægges til rumsondens højde over Merkurs overflade. Det giver:

   F = (6,67·10^-11 N·m²·kg^-2)·(3,29·10²³ kg)·(512 kg)/(2,439·10⁶ m + 2,00·10⁵ m)² = 1613,29 N

   Dvs. tyngdekraften på rumsonden er 1,61·10³ N

3. Man beregner rumsondens fart ud fra dens kinetiske energi i den største højde over Merkurs overflade. Det antages, at der gælder bevarelse af mekanisk energi for rumsonden (intet tab af mekanisk energi i form af gnidningsvarme).

   Den mekaniske energi for rumsonden i lav højde over Merkurs overflade kaldes E_m,1 og den mekaniske energi i den største højde kaldes E_m,2.

   Tilsvarende er E_k,1 dens kinetiske energi i lav højde, E_k,2 dens kinetiske energi i stor højde, E_p,1 dens potentielle energi i lav højde, mens E_p,2 er dens potentielle energi i stor højde.

   Man skal finde E_k,2 og får:

   E_m,1 = E_m, ⇒ E_k,1 + E_p,1 = E_k,2 + E_p,2 ⇒ E_k,2 = E_k,1 + E_p,1 - E_p,2.

   Formlen for den potentielle energi i et tyngdefelt er E_p = -G·M·m/r. (Nulpunktet for den potentielle energi ligger i det uendelige.) Dvs:

   E_p,1 = -(6,67·10^-11 N·m²·kg^-2)·(3,29·10²³ kg)·(512 kg)/(2,439·10⁶ m + 2,00·10⁵ m) = −4,257·10⁹ J.

   E_p,2 = -(6,67·10^-11 N·m²·kg^-2)·(3,29·10²³ kg)·(512 kg)/(2,439·10⁶ m + 1,56·10⁷ m) = −6,228·10⁸ J.

   Den kinetiske energi fra spørgsmål a) sættes sammen med de fundne potentielle energier ind i formlen for E_k,2:

   E_k,1 + E_p,1 - E_p,2 = 3,716·10⁹ J + (−4,257·10⁹ J) − (−6,228·10⁸ J) = 8,1·10⁷ J.

   Heraf finder man farten i det højeste punkt på banen:

   solve(0.5*512*kg*v²=8.1*10⁷*kg*met²*sek^-2,v) ▸ v=562.5*met/sek or v=−562.5*met/sek

   Dvs. farten i ellipse-banens højeste punkt er 5,6·10² m·s^-1

   Bemærkning: Resulatet passer med Keplers anden lov, der indebærer, at farten i satellitbanenes fjerneste punkt er mindre end i det laveste.

Svar på opgave 6: Betelgeuse

1. For at beregne radius af Betelgeuse i 1993 skal man bruge Stefan-Boltzmanns lov for en stjernes effektive temperatur:

   L₁₉₉₃ = σ·4·π·(R₁₉₉₃)²·(T₁₉₉₃)⁴, hvor

      L₁₉₉₃ = 2,12·10³¹ W·m^-2 er Betelgeuses strålingsintensitet i 1993,

      σ = 5,670367·10^-8 W·m^-2·K^-4 er en konstant

      R₁₉₉₃ er Betelgeuses radius i m i 1993 (som skal findes) og

      T₁₉₉₃ = er Betelgeuses effektive temperatur i K i 1993. Denne beregnes ud fra den nuværende:

       T_nu = 1,085·T₁₉₉₃ ⇒ T₁₉₉₃ = 3450 K/1,085 = 3179,72 K.

   Man finder Betelgeuses radius:

   solve(2.12*10³¹*wat=5.67*10^-8*wat*met^-2*kel^-4*4*π*r²*(3180*kel)⁴,r) ▸ r=5.395*10¹¹*met or r=−5.395*10¹¹*met

   Dvs. Betelgeuses radius er 5,40·10¹¹ m

2. For at finde Betelgeuses lysstyrke skal man bruge afstandskvadratloven: L = I·4·π·R², hvor

      L er Betelgeuses lysstyrke i W,

      I = 3·10^-3 W·m^-2 er Betelgeuses strålingsintensitet ved jorden og

      R = 640 lysår er afstanden mellem jorden og Betelgeuse. Denne omregnes til meter,

      idet 1 lysår er 9,46·10¹⁵ m. Man får: R = (640 ly)·(9,46·10¹⁵ m/ly) = 6,05·10¹⁸ m.

   Dvs. Betelgeuses lysstyrke forventes at være følgende, når den eksploderer:

   3·10^-3 W·m^-2·4·π·(6,05·10¹⁸ m)² = 1,4·10³⁶ W

Svar på opgave 7: Stort badebassin

1. Solinstrålingens intensitet på en gennemsnits sommerdag i Danmark er 20 MJ/m².

   Det antages, at solen er den eneste energikilde.

   Det antages, at al solenergi optages i vandet.

   Det antages, at varme ikke udveksles med omgivelserne (i praksis vil vandet være lidt varmere end omgivelserne om morgenen og om aftenen, mens det vil være lidt koldere end omgivelserne midt på dagen).

   Opvarminingen af vandet følger formlen: Q = ρ_v·A·H·c_v·ΔT. Heri indsættes Q = I·A, der giver formlen: ΔT = I/(ρ_v·H·c_v).

   Forklaring:

      Q er den samlede energi fra solen, der modtages af bassinet,

      I er intensiteten af solenergi i J·m^-2 ved jordoverfladen,

      A er vandoverfladens areal i m²,

      ρ_v er vands densitet i kg/m³,

      H er bassinets højde i m,

      c_v er vands specifikke varmekapacitet i J/(kg·K) og

      ΔT er temperaturændringen i K eller °C.

   Det ses, at ΔT i denne formel er uafhængig af vandoverfladens areal.

   Ud fra billedet anslår man H til 1,2±0,1 m. ρ_v slås op til 1,000 kg/m³. C_v slås op til 4,182 kJ/(kg·K). Dette giver følgende formel for ΔT:

   Beregning af usikkerhed: Ved at lave samme beregning for største henholdsvis mindste anslåede værdi af H, får man: ΔT_min = 3,7 °C og ΔT_max = 4,3 °C. (Bemærk: jo dybere bassin, jo mindre temperaturstigning).

   Dvs. vandets temperatur stiger med 4,0±0,3 °C i løbet af dagen.