Svar på opgave 1: Stjernen Vega

1. Den punkterede kurve er Plancks strålingskurve for Vega. Den effektive overfladetemperatur af stjernen bestemmes ud fra kurvens toppunkt og ved hjælp af Wiens forskydningslov.

   Den bølgelængde (λ_max), hvor kurven har toppunkt aflæses som vist nedenunder til: λ_max = (5,03±0,03)·10² nm = (5,03±0,03)·10²·10^-9 m = (5,03±0,03)·10^-7 m.

   

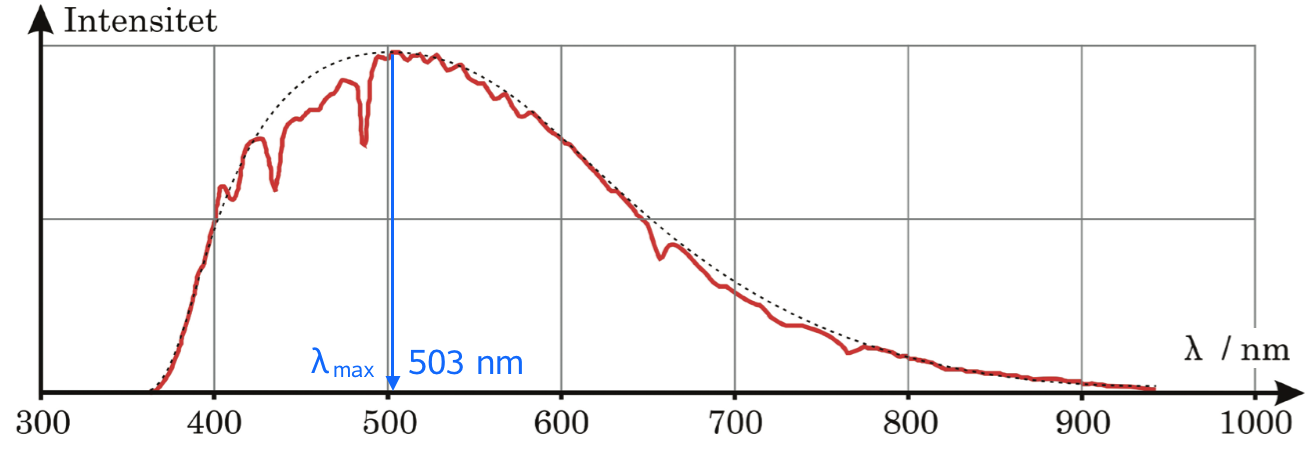
   Wiens forskyningslov siger: λ_max = (2,989·10^-3 m·K)/T_e, hvor

   T_e er stjernens effektive overfladetemperatur i K. Man får i Ti-Nspire:

   solve(5.03*10^-7*meter=2.989*10^-3*meter*kelvin/t,t) ▸ t=5942.35*kelvin

   Dvs. den effektive overfladetemperatur af Vega er, når man tager hensyn til aflæsnings-usikkerheden, lig med: 5,9·10³ K

2. Afstanden mellem Vega og jorden findes ved hjælp af afstandskvadratloven, som er:

   L = I·4·π·R², hvor

      L = 1,42 ⋅10²⁸ W er Vegas lysstyrke,

      I = 2,00⋅10^-8 W/m² er intensiteten af Vegas lys ved jordoverfladen og

      R er afstanden mellem jorden og Vega i m, som skal findes.

   Man får:

   solve(1.42*10²⁸*watt=(2.*10^-8*watt/meter²)*4*π*r²,r) ▸ r=2.37697*10¹⁷*meter or r=−2.37697*10¹⁷*meter (den negative værdi er ugyldig).

   Dvs. afstanden mellem jorden og Vega er 2,38·10¹⁷ m

Svar på opgave 2: Knivkast

1. Kniven opbremses af en konstant gnidningskraft (F). Denne gnidningskrafts arbejde er lig med knivens kinetiske energi lige inden sammenstødet med skiven.

   Dvs. F·Δs = 0,5·m·v² ⇒ F = 0,5·m·v²/Δs, hvor

      Δs = 0,006 m er den strækning, som kniven tilbagelægger fra den rammer skiven indtil den
         stopper,

      m = 0,210 kg er knivens masse og

      v = 13,6 m/s er knivens fart lige før sammenstødet med skiven. Det forudsættes, at kniven ikke
         mister fart på grund af luftmodstand.

   Man får: F = 0,5·(0,21 kg)·(13,6 m·s^-1)²·(0,006 m)^-1 = 3236,8 N

   Dvs. gennemsnitskraften på kniven er 3·10³ N

2. Der er tale om et skråt kast med negativ elevationsvinkel. Man skal finde sluthøjden i forhold til jordoverfladen. Der ses bort fra luftmodstand.

   Formlen for landingshøjden (y) i m af et skråt kast er:

   y = −0,5·g·(v₀)^-2·(cos(α))^-2·x² + tan(α)·x + y₀, hvor

      g = 9,82 m·s^-2 er tyngdeaccelerationen,

      v₀ = 15,3 m·s^-1 er begyndelsesfarten af kniven,

      α = −8,4° er kastevinklen i forhold til vandret (positiv retning opad),

      y₀ = 1,1 m er kastehøjden og

      x er kastelængden i m.

   Man indsætter tallene i formlen og får: y = −0,0205·x² − 0,148·x + 1,1 (enheden for x og y er m). Dette polynomium indtegnes i et koordinatsystem sammen med en skitse af målskiven lavet i Geogebra:

   

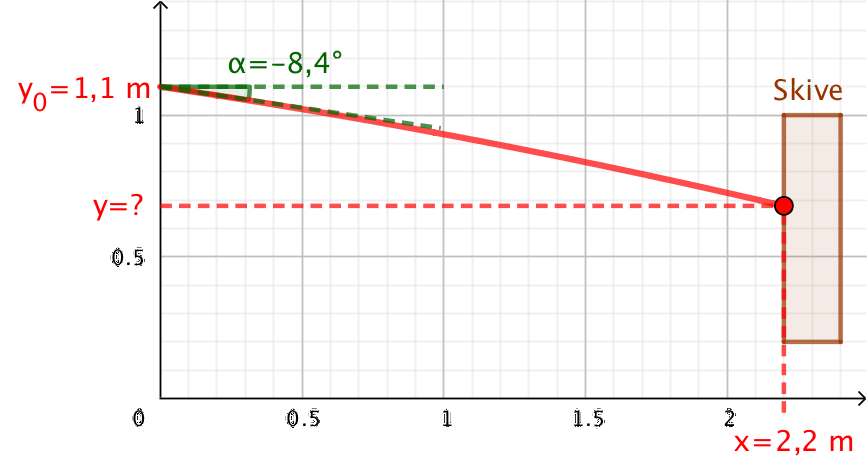
   Som det ses, passer kurven med oplysningerne om kastevinkel og den højde, som kniven kastes fra. Man indsætter x = 2,2 m i formlen for y:

   y = (−0,0205·2,2² − 0,148·2,2 + 1,1) m = 0,676 m

   Dvs. kniven rammer skiven i højden 0,68 m over jorden.

Svar på opgave 3: Sukker

1. Man aflæser fire sammenhængende punkter for masse (i kg) og volumen (i L) af sukker og tilføjer til sidst punktet (0,0), som man ved skal ligge på kurven.

   Man vælger følgende masser på skalaen: 0,2; 0,4; 0,6 og 0,9 kg. Disse tal oprettes som en liste i Ti-Nspire:

   masse:={0,0.2,0.4,0.6,0.9} ▸ {0,0.2,0.4,0.6,0.9}

   Man beregner voluminerne i Geogebra, hvor billedet af skalaen lægges ind.

   

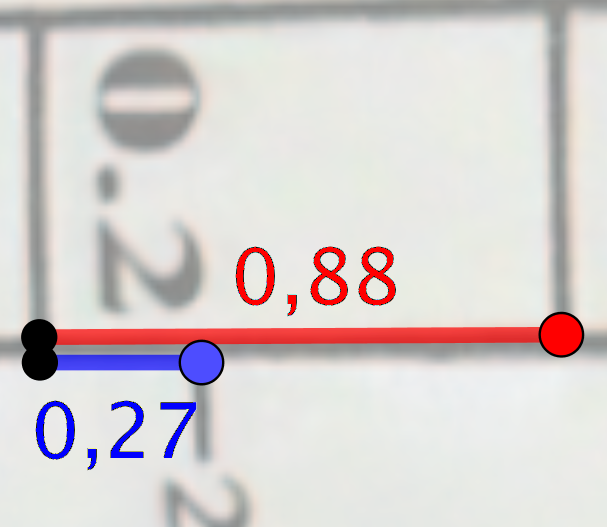
   Overfor er vist beregningen af voluminet af 0,2 kg sukker. Den blå prik angiver punktet på skalaen for 0,2 kg sukker.

   Dette punkt befinder sig i intervallet mellem 0,2 L og 0,3 L. Volumen af interval = 0,1 L.

   Afstanden fra starten af intervallet til punktet er 0,27 enheder. Hele intervallets længde måles dernæst til 0,88 enheder. Enheden stammer fra det koordinatsystem i Geogebra, som billedet er lagt ind i.

   Volumenet af 0,2 kg sukker findes dernæst ved lineær interpolation til 0,2 L + (0,1 L)·(0,27/0,88) = 0,231 L.

   På samme måde findes volumenerne af de andre sukker-masser og de sættes ind i en liste i Ti-Nspire:

   volumen:={0,0.2+0.1*(27/88),0.4+0.1*(59/81),0.7+0.1*(0.06/76),1.+0.1*(38/69)} ▸ {0,0.2307,0.4728,0.7001,1.0551}

   De sammenhørende værdier af volumen og masse af sukker sættes ind i et diagram i Ti-Nspire:

   

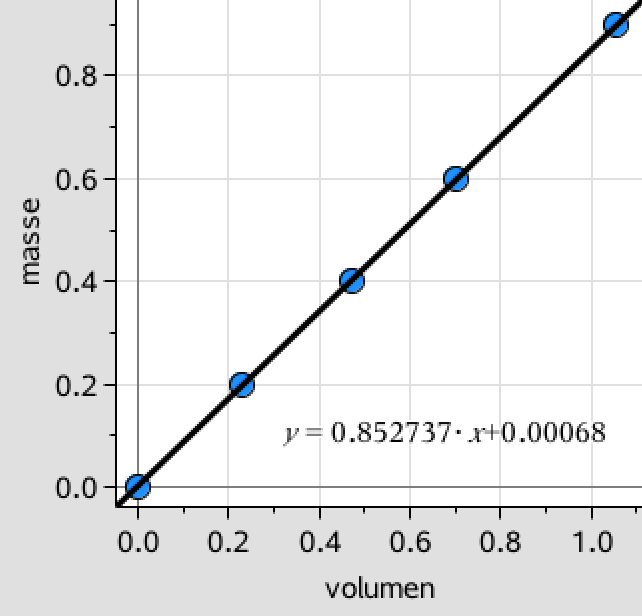
   Man får som vist regressionskurven: y = (0,852737 kg/L)·x + 0,00068 kg, når man afbilder massen af sukker mod volumenet.

   Afrundet til to decimaler er ligningen for kurven: y = (0,85 kg/L)·x.

   Massefylde af sukkeret er forholdet mellem masse og volumen for sukker, som er lig med hældningen til kurven eller koefficienten for x, der er 0,85 kg/L

   Bemærkninger:

   Det giver i følge bedømmelses-vejledningen ikke fuld point kun at se på eet punkt på skalaen.

   Tabelværdien er ca. dobbelt så stort det fundne. Det skyldes, at det, som man finder i opgaven, er massefylden af sukkerkrystaller plus hulrum og ikke af krystaller alene.

Svar på opgave 4: Elektrisk køletaske

1. Formlen for den omsatte elektriske energi i køle-elementet er:

   Q = U·I·Δt, hvor

      Q er energien i J,

      U = 12 V er elementets spænding,

      I = 4,2 A er elementets strømstyrke og

      Δt = 3 timer = 3·3600 s = 10800 s er tiden.

   Man får: Q = (12 V)·(4,2 A)·(10800 s) = 544320 J = 5,4·10⁵ J

2. Nedenstående principtegning viser tasken med blåt og de effekter (målt i W), der indgår i beregningen.

   

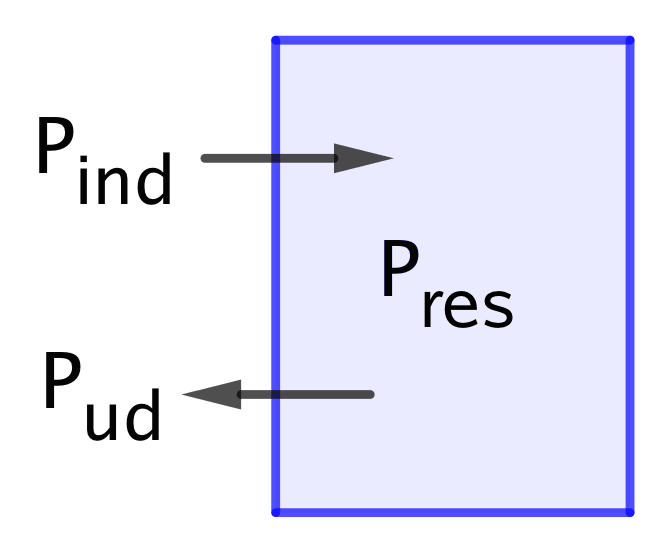
      P_ind er den indgående effekt, som er en funktion af tiden. Den regnes med positivt fortegn og
         skabes rent fysisk af, at omgivelserne er varmere end tasken,

      P_ud = -18 W er den udgående effekt (altid negativ), som skyldes køleelementet, eller at tasken er
         varmere end omgivelserne og

      P_res er den resulterende eller akkumulerede effekt i tasken som funktion af tiden. Der gælder
         at P_res = P_ind + P_ud. P_res er positv, når tasken opvarmes og negativ, når den afkøles.

   Man skal finde P_ind ved t = 2000 s, som findes af kurven, der viser temperatur-udviklingen i tasken.

   For den resulterende effekt og temperaturændringen i tasken ved t = 2000 s gælder:

   P_res,t=2000s = C·T'(2000s), hvor

      C = 2,4 kJ/K er taskens varmekapacitet og

      T'(2000s) er taskens temperaturændringen i °C eller K til tiden 2000 s.

   T'(2000 s) beregnes som hældningen til kurven for t=2000s:

   

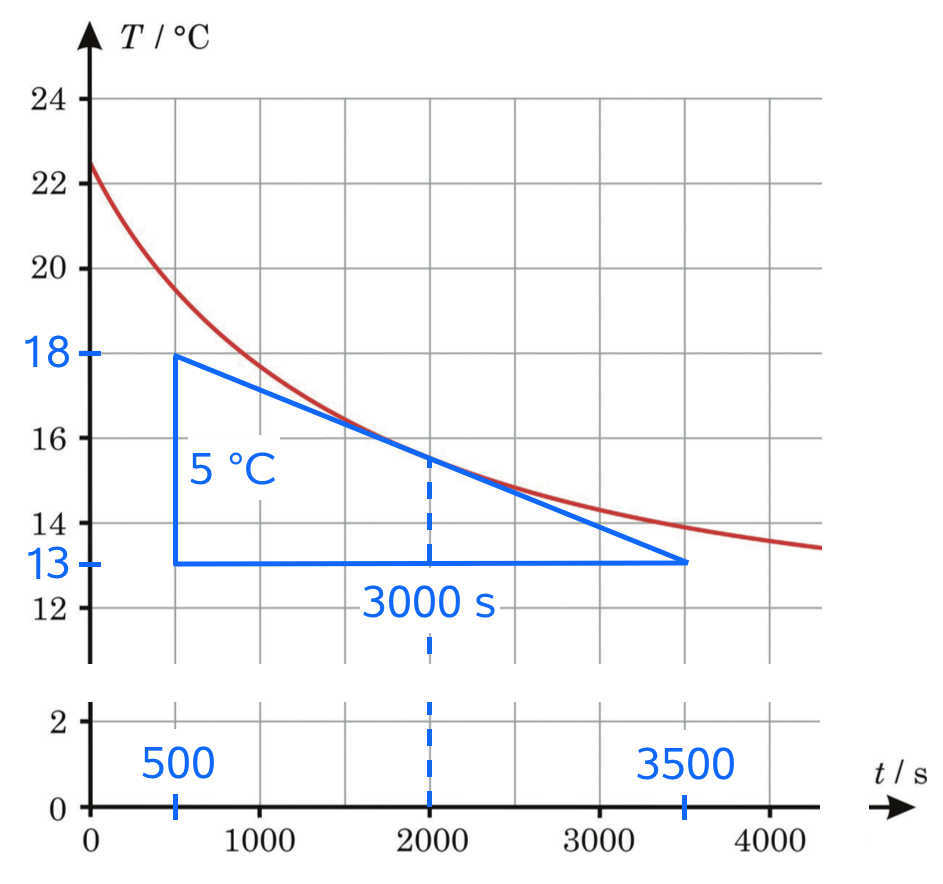
   Dvs. P_res,t=2000s = (2,4 kJ/K)·(13 K - 18 K)/(3500 s - 500 s) = (2400 kJ/K)·(-5 K)/(3000 s) = -4 W.

   P_ind = 18 W - 4 W = 14 W, der er den effekt, som tasken tilføres fra omgivelserne ved t = 2000 s.

Svar på opgave 5: Katastrofen i Kyshtym

1. I følge Databog i Fysik og Kemi udgave 16 så henfalder Ce-144 ved beta-henfald:

   

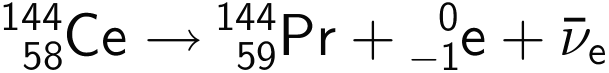
2. Man finder massen af Ce-144 nukilder (m) ved hjælp af formlen:

   m = A·T·ln(2)^-1·M, hvor

      A = 24,4 PBq = 24,4·10¹⁵ s^-1 er aktiviteten,

      T = 284,6 døgn = (284,6 døgn)·(24·3600 s/døgn) = 2,459·10⁷ s er halveringstiden for Ce-144
         og

      M = (143,9 u)·(1,661·10^-27 kg/u) = 2,390·10^-25 kg er massen af det enkelte Ce-144 nuklid.

   Man får: m = (24,4·10¹⁵ s^-1)·(2,459·10⁷ s)·ln(2)^-1·(2,390·10^-25 kg) = 0,2069 kg

   Dvs. massen af Ce-144 er 0,207 kg

3. For at beregne det tidspunkt, hvor aktiviteten af de to stoffer er ens, skal man løse ligningen:

   A_Ce-144(t) = A_Sr-90(t) ⇒ A_Ce-144(0)·0,5^t/T_Ce = A_Sr-90(0)·0,5^t/T_Sr. Her er

      A_Ce-144(0) = 24,4 PBq er startaktiviteten for Ce-144,

      A_Sr-90(0) = 2,0 PBq er startaktiviteten for Sr-90,

      T_Ce = 2,459·10⁷ s er halveringstiden for Ce-144 og

      T_Sr = (29,1 år) = (29,1 år)·(365,25 døgn/år)·(24·3600 s/døgn) = 9,183·10⁸ s er halveringstiden
         for Sr-90.

   Dette giver den færdige ligning, som løses i Ti-Nspire:

   solve(24.4*PBq*0.5^{t/(2.459*107*s)}=2.0*PBq*0.5^{t/(9.183*108*s)},t) ▸ t=9.11823·10⁷*s or pbq=0.

   Dvs. der går 9,1·10⁷ s før aktiviterne af Ce-144 og Sr-90 er ens.

Svar på opgave 6: Pedaltraktortræk

1. Accelerationen findes ved hjælp af Newtons anden lov:

   F = a·m ⇒ a = F/m, hvor

      F = 41 N er den resulterende kraft på traktoren,

      a er traktorens acceleration i m/s² og

      m = 190 kg er traktorens masse.

   Man får: a = (41 N)/(190 kg) = 0,22 m/sek²

2. Man opretter lister i Ti-Nspire med tid og strækning:

   tid:={0.,1.,2.,3.,4.,5.,6.,7.} ▸ {0.,1.,2.,3.,4.,5.,6.,7.}

   strækning:={0.,0.85,1.65,2.35,3.,3.65,4.1,4.35} ▸ {0.,0.85,1.65,2.35,3.,3.65,4.1,4.35}

   Disse lister sættes ind i en graf, og man laver en anden- og tredjegradspolynomie regression, der på øjemål ser ud til at give den bedste tilnærmelse.

   

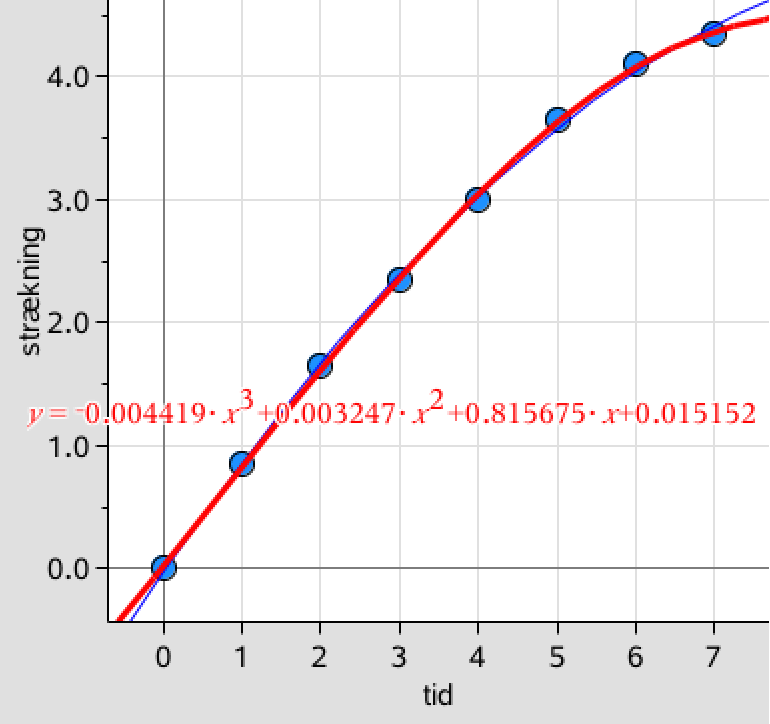
   Tredjegradspolynomie-regressionen, som ligger tættest på punkterne, er fremhævet med rødt, mens andengrads-polynomiet er blå. Tredjegrads-polynomiet har formlen: s(t) = −0,00442·t³ + 0,00325·t² + 0,816·t + 0,0152.

   Farten til tiden t = 4 sek er s'(4). Man har: s'(t) = −0,01326·t² + 0,0065·t + 0,816, som giver:

   s'(4) = −0,01326·4² + 0,0065·4 + 0,816 m/sek = 0,630 m/sek

   Dvs. traktorens fart efter 4 sekunder er 0,63 m/sek

3. Den gennemsnitlige effekt P findes ved hjælp af formlen:

   P = ΔA/Δt, hvor

      ΔA er gnidningskraftens arbejde over strækningen 10,0 m og

      Δt = 13,1 sek er tiden som gnidningskraftens arbejde tager.

   ΔA = findes ved at integrere dA(s) = F(s)·ds fra s = 0 til s = 10,0 m. Her er F(s) er gnidningskraften som funktion af strækningen, s.

   Idet F(s) = (105 N/m)·s + 84N, så får man, at ΔA =

   

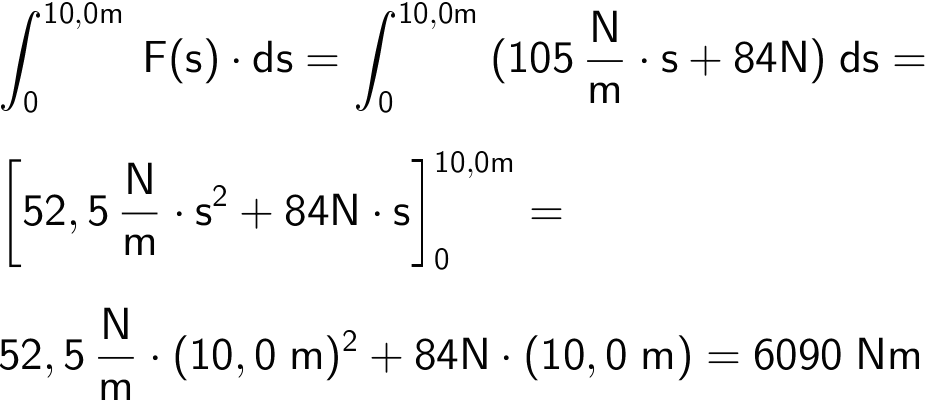
   Dvs. gnidningskraftens gennemsnitlige effekt under trækket er

   (6090 Nm)/(13,1 sek) = 464,9 J/sek = 465 W

Svar på opgave 7: Alnilam

1. Alnilam's lystyrke i W (L) findes ved hjælp af Stefan-Boltzmann's lov:

   L = 4·π·R²·σ·T⁴, hvor

      R = 1,81⋅10¹⁰ m er stjernens radius,

      σ = 5,6704·10^-8 W·m^-2·K^-4 og

      T = 2,5⋅10⁴ K er stjernens effektive overfladetemperatur.

   Man får L = 4·π·(1,81⋅10¹⁰ m)²·(5,6704·10^-8 W·m^-2·K^-4)·(2,5⋅10⁴ K)⁴ = 9,119·10³¹ W.

   Dvs. Alnilam's lystyrke er 9,1·10³¹ W

2. Man beregner tyngdeaccelerationen ved Alnilam's overflade ved at kombinere formlen for massetiltrækning: F = G·M·m/R² med Newtons anden lov F = a·m, idet det forudsættes, at stjernen er kugleformet. Dette giver (idet m og F går ud):

   a = G·M/R². Her er

      a tyngdeaccelerationen ved stjernens overflade i m/s²,

      G = 6,67 N·m²·kg^-2 er gravitationskonstanten,

      M er stjernens masse i kg og

      R = 1,81·10¹⁰ m er stjernens radius.

   Stjernens masse er 40 gange solens, hvis masse slås op til 1,989.10³⁰ kg, dvs. M = 40·1,989.10³⁰ kg = 7,956·10³¹ kg.

   Man får: a = (6,67 N·m²·kg^-2)·(7,956·10³¹ kg)/(1,81·10¹⁰ m)² = 16,1981 N·kg^-1 = 16,1981 m·s^-2.

   Dvs. tyngdeaccelerationen ved Alnilam's overflade er 16,2 m/s²