Svar på opgave 1: Türanor

1. Nyttevirkningen er (udnyttet energi)/(tilført energi).

   Udnyttet energi = 93,5 kW = 9,35·10⁴ W.

   Tilført energi = (930 W/m²)·(536 m²) = 5,0·10⁵ W

   Dvs. nyttevirkningen er (9,35·10⁴ W)/(5,0·10⁵ W) = 0,19 = 19 %

2. Det antages, at batteriets nyttevirkning er 100 %, dvs. at al oplagret energi omsættes til fremdrift.

   Den tilbagelagte strækning er v·Δt, hvor v er farten og Δt er tiden.

   Farten v = 14 km/h = 14/3,6 m·s^-1 = 3,89 m·s^-1.

   Der gælder: P = ΔE/Δt ⇒ Δt = ΔE/P, hvor P er motorens effekt (=20 kW) og ΔE er den oplagrede energi (= 4,7 GJ).

   Man får: Δt = (4,7 GJ)/(20 kW) = (4,7·10⁹ J)/(2,0·10⁴ J·s^-1) = 2,35·10⁵ s.

   Dvs. skibet tilbagelægger: v·Δt = (3,89 m·s^-1)·(2,35·10⁵ s) = 9,14·10⁵ m = 914 km på een opladning af batteriet.

Svar på opgave 2: Stålværk

1. Effekten kaldes P, mens spændingen kaldes U og strømstyrken kaldes I.

   Man har, at: P = U·I ⇒ I = U/P = (40 MW)/(900 V) = (40·10⁶ W)/(900 V) = 4,4·10^-4 A.

   Dvs. strømstyrken gennem jernet er 4,4·10⁴ A

2. Det antages, at jernet skal opvarmes fra 25 °C til smeltepunktet (1538 °C) og derefter smeltes. Ligeledes antages, at der ikke er varmetab til omgivelserne.

   Der gælder formlen: P = m·(c_p·ΔT + L)/Δt ⇒ Δt = m·(c_p·ΔT + L)/P, hvor

      m er massen af jern = 8,0·10⁴ kg,

      c_p er den specifikke varmekapacitet af jern = 449 J·kg^-1·K^-1,

      ΔT er temperaturændringen under opvarmningen = 1538 °C - 25 °C = 1513 K,

      L den specifikke smeltevarme for jern = 275·10³ J·kg^-1 og

      Δt er den tid som opvarmning og smeltning tager.

   Man får: Δt = (8,0·10⁴ kg)·((449 J·kg^-1·K^-1)·(1513 K) + 275·10³ J·kg^-1)/(4,0·10⁷ J·s^-1) = 1,9·10³ s.

   Dvs. det tager 1,9·10³ s = (1,9·10³)·(1/60 min.) = 32 min. at smelte jernet.

Svar på opgave 3: Dobbeltstjernen Sirius

1. Man bruger Wiens forskydningslov: λ_max = (2,898·10^-3 K·m)/T, hvor

      λ_max den bølgelængde, der giver den højeste intensitet og

      T er den absolutte effektive overfladetemperatur på stjernen = 2,48⋅10⁴ K.

   Dvs. den bølgelængde, hvor intensitetsfordelingen har sit maksimum, er
      (2,898·10^-3 K·m)/(2,48⋅10⁴ K) = 1,17·10^-7 m = 117 nm

2. Densiteten af stjernen er ρ = m/V, hvor

      m er stjernens masse = 2,09·10³⁰ kg og

      V er stjernens rumfang = (4/3)·π·R³, hvor R er stjernens radius, idet det antages, at stjernen er
      kugleformet.

   Stjernens radius findes ved hjælp af Stefan-Boltzmanns lov, idet man har:

   L = 4·π·R³·σ·T⁴ ⇒ R = √[L/(4·π·σ·T⁴)], hvor

      L er stjernens luminositet eller samlede effekt = 9,95⋅10²⁴ W og

      σ er Stefan-Boltzmanns konstant = 5,67·10^-8 W·m^-2·K^-4.

   Dette giver med hensyn til radius: R = √[(9,95⋅10²⁴ W)/(4·π·(5,67·10^-8 W·m^-2·K^-4)·(2,48⋅10⁴ K)⁴)] = 6,08·10⁶ m

   Dette indsættes i formlen for densitet: ρ = m/((4/3)·π·R³) = (3/(4·π))·(2,09·10³⁰ kg)/(6,08·10⁶ m)³ = 2,22·10⁹ kg/m³

   Dvs. Sirius B's gennemsnitlige densitet er 2,22·10⁹ kg/m³ (Tabelværdi: 2,38·10⁹ kg/m³.)

Svar på opgave 4: Meget gammelt vand

1. Kr-81 omdannes til Br-81 ved elektronindfangning. En elektron fra den inderste skal i Kr-81 (K-skallen) indfanges af kernen, hvor en proton omdannes til en neutron. Samtidig afgives en neutrino. Reaktionsskema:

   

2. Aktiviteten (A) er antallet af kerner, der henfalder pr. sekund af Kr-81. For aktiviteten gælder:

   A = k·N, hvor

      k er henfaldskonstanten og

      N er antallet af Kr-81 kerner.

   For henfaldskonstanten gælder: k = ln(2)/T_1/2 = ln(2)/(0,21·10⁶ år) = 3,30·10^-6 år^-1.

   Man får: A = (3,30·10^-6 år^-1)·(2,32·10⁶) = 7,66 år^-1 = 7,66·(365,25·24·3600 s)^-1 = 2,43·10^-7 s^-1.

   Dvs. aktiviteten af Kr-81 er 2,43·10^-7 henfald pr. sek.

3. Der gælder: N(t₁) = N(t₀)·e^{-k·(t₁ - t₀)}, hvor .

      N(t₀) er antallet af kerner i grundvandet til tidspunktet t₀ hvor vandet sivede ned. Dette antages at have haft samme indhold af kerner som overfladevand idag = 1900 kerner/liter.

      N(t₁) er antallet af kerner i grundvandet til tidspunktet t₁, der er det nuværende tidspunkt = 450 kerner/liter.

   Man skal finde (t₁ - t₀) og betragter 1 liter vand:

   450 = 1900·e^{-(3,30·10-6 år-1)·(t₁ - t₀)} ⇒

   t₁ - t₀ = ln(450/1900)/(-(3,30·10^-6 år^-1)) ⇒

   t₁ - t₀ = 4,36·10⁵ år.

   Dvs. alderen af vandet under Farafra er 4,36·10⁵ år.

   Vandet har bevæget sig 220 km fra Gum Horia til Farafra. Dette tager 4,36·10⁵ år - 2,30·10⁵ år = 2,06·10⁵ år. Dvs. den gennemsnitlige fart er :

   Δs/Δt = (220 km)/(2,06·10⁵ år) = 0,001068 km/år = 1,07 m/år. (= 3,38·10^-8 m/s.)

Svar på opgave 5: Enterprise

1. Farten, v, er lig med (omløbsbane)/(omløbstid) = 2·π·r/T, hvor

      r er radius i cirkelbanen = 5,3 m og

      T er omløbstiden = 4,2 s.

   Dvs. kabinens fart er 2·π·(5,3 m)/(4,2 s) = 7,9 m·s^-1

2. Den resulterende kraft, F_R, i en jævn cirkelbevægelse er lig med centripetalkraften, der peger fra massemidtpunktet af kabinen ind mod cirklens centrum, og som har længden:

   m·v²/r, hvor

      m er massen af kabine med passagerer = 215 kg. Dermed er:

   |F_R| = (215 kg)·(7,9 m·s^-1)²/(5,3 m) = 2,5·10³ N.

   Den resulterende kraft er summen af to kræfter: Tyngdekraften F_T og snorkraften, F_S.

   Tyngdekraften går lodret nedad fra kabinens tyngdepunkt. Snorkraften går fra tyngdepunktet op gennem hængslet.

   |F_T| = m·g = (215 kg)·(9,82 m·s^-1) = 2,1·10³ N.

   F_S findes som vektordifferensen: F_R - F_T. Da de to vektorer danner en retvinklet trekant med F_S som hypotenusen, så kan længden af F_S findes ved hjælp af Pythagoras læresætning:

   |F_S| = √[(2,5·10³ N)² + (2,1·10³ N)²] = 3,3·10³ N.

   Disse kræfter er tegnet ind på diagrammet som vist nedenunder:

   

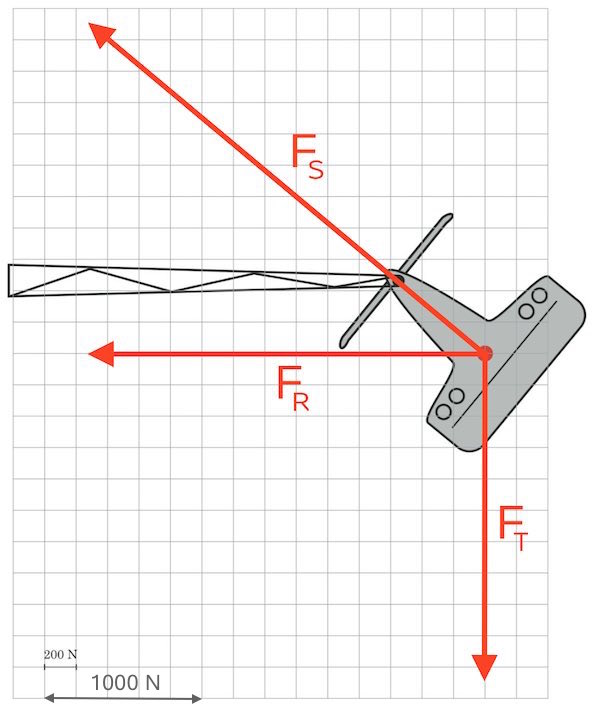
   Man kan også måle vinklen mellem F_S og F_R. Kaldes denne θ, så kan man benytte formlen |F_R| = |F_S|·cos(θ) til at finde |F_S|.

Svar på opgave 6: E-bike

1. Ved konstant fart gælder: s(t) = v·t, hvor

      s(t) er stedet som funktion af tiden,

      v er farten og

      t er tiden.

   Man får: t = (5,0 km)/(25 km/h) = 0,2 h = 0,2·(60 min) = 12 min.

   Dvs. det tager 12 minutter at tilbagelægge strækningen.

2. Ved konstant accelerration gælder: s(t) = 0,5·a·t² ⇒ t = s(t)/v, hvor

      a er accelerationen og

      t er tiden.

   Man opretter lister for tid og sted i Ti-Nspire:

   tid:={0,1.,2,3,4,5,6} ▸ {0,1.,2,3,4,5,6} .

   sted:={0,0.6,2.4,5.4,9.6,15,21.6} ▸ {0,0.6,2.4,5.4,9.6,15,21.6}

   Man laver et plot for s(t) som vist nedenunder (idet y(x) = s(t)):

   

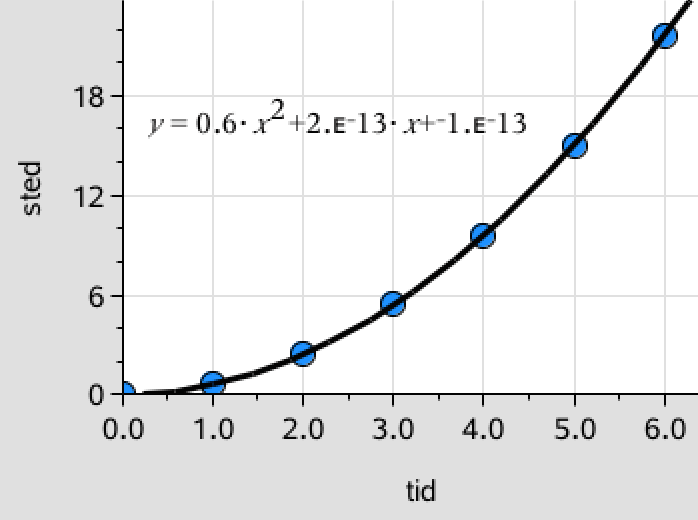
   Tendenskurven på figuren er en regressionskurve for et andengradspolynomium (man kan ikke lave en potens-regression, når punktet (0,0) er med).

   Det ses, at s(t) = 0,6·t² tilnærmelsesvis. Heraf ses, at 0,6 = 0,5·a ⇒ a = 1,2 m·s^-2.

   Farten som funktion af tiden, v(t) = a·t for konstant acceleration.

   Dette giver her, at: v(t) = (1,2 m·s^-2)·t.

   Man finder farten i m·s^-1: 25 km/h = (25·10³ m)/(3600 s) = 6,9 m·s^-1.

   Ligningen v(t) = 6,9 m·s^-1 løses med hensyn til t: (1,2 m·s^-2)·t = 6,9 m·s^-1 ⇒ t = 5,75 s

   Dvs. cyklisten når farten 25 km/h efter 5,8 s

3. Den samlede effekt som funktion af tiden kaldes P(t). Denne er lig med skalarproduktet af kraftens vektor og hastighed, der her er kraftens størrelse gange farten, da kraft og hastighed har samme retning.

   Størrelsen af kraften på e-biken er: m·a = (65,2 kg)·(1,2 m·s^-2) = 78,2 N.

   Dermed er P(t) = (78,2 N)·v(t) = (78,2 N)·(1,2 m·s^-2)·t = (93,9 N·m·s^-2)·t = (93,9 W/s)·t.

   Dermed stiger den samlede effekt konstant, og maksimum indtræder dermed efter 6,0 sekunder. Den største effekt, som cyklisten skal tilføre, er dermed den samlede effekt efter 6,0 sekunder minus 250 W, som giver: (93,9 W/s)·(6 s) - 250 W = 313 W.

   Dvs. den største effekt, som cyklisten tilfører e-biken under accelerationen, er 313 W

Svar på opgave 7: Metro

1. Trykket inde i forreste vogn ved konstant fart, og når toget står stille, er lig med atmosfærens tryk (=100,98 kPa).

   Den del af trykket, der ligger over dette, skyldes kraften fra den luft, som toget skal bremse. Denne kraft er lig med luftens masse gange dens acceleration, hvor accelerationen er opbremsningen.

   Den maksimale acceleration findes ved den maksimale trykændring (= 101,03 kPa - 100,98 kPa = 50 Pa = 50 N·m^-2). Dette er vist på figuren nendenunder:

   

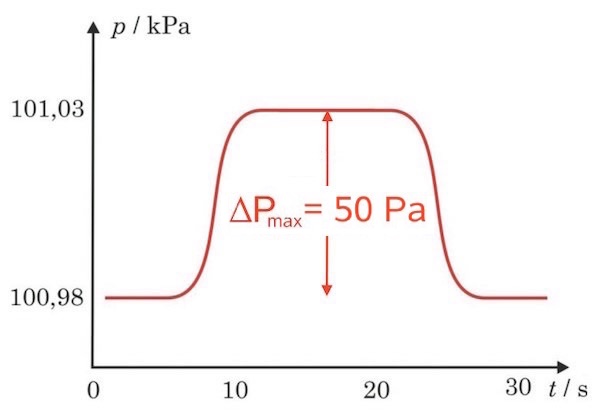
   Der gælder følgende sammenhæng mellem den maksimale trykændring (ΔP_max) og accelerationen (a):

   ΔP_max = F_max/A ⇒ ΔP_max = m·a_max/A ⇒ ΔP_max = ρ·A·L·a_max/A ⇒

   a_max = ΔP_max/(ρ·L), hvor

      F_max er luftens maksimale kraft under opbremsningen (erstattes af: m·a_max),

      m er luftens masse inde i toget (erstattes af: ρ·A·L),

      ρ er luftens densitet = 1,21 kg·m^-3,

      A er togets tværsnitsareal (går ud i beregningen) og

      L er togets længde = 38,5 m. Man får:

   a_max = (50 N·m^-2)/((1,21 kg·m^-3)·(38,5 m)) = (50 kg·m·s^-2·m^-2)/((1,21 kg·m^-3)·(38,5 m)) =
   1,07 m·s^-2.

   Dvs. den maksimale acceleration under opbremsningen er 1,1 m·s^-2