Svar på opgave 1:

1. 2·(x + 5) = 6·x + 30 ⇔

   2·x + 10 = 6·x + 30 ⇔

   2·x - 6·x = 30 - 10 ⇔

   -4·x = 20 ⇔

   x = -5

Svar på opgave 2:

1. Modellen er f(x) = 39.000x + 526.000,

   hvor f(x) er produktionen af kvartssand i kubikmeter, og x er antal år efter 2006.

Svar på opgave 3:

1. Toppunktet har koordinatsættet: (x_T,y_T) = (-b/(2a),c-b²/(4a)). I dette tilfælde er a = 2, b = -4 og c = 7. Man får:

   x_T = -(-4)/(2·2) = 1

   y_T = 7 - 4²/(4·2) = 7 - 16/8 = 5

   Dvs. toppunktet er (1,5)

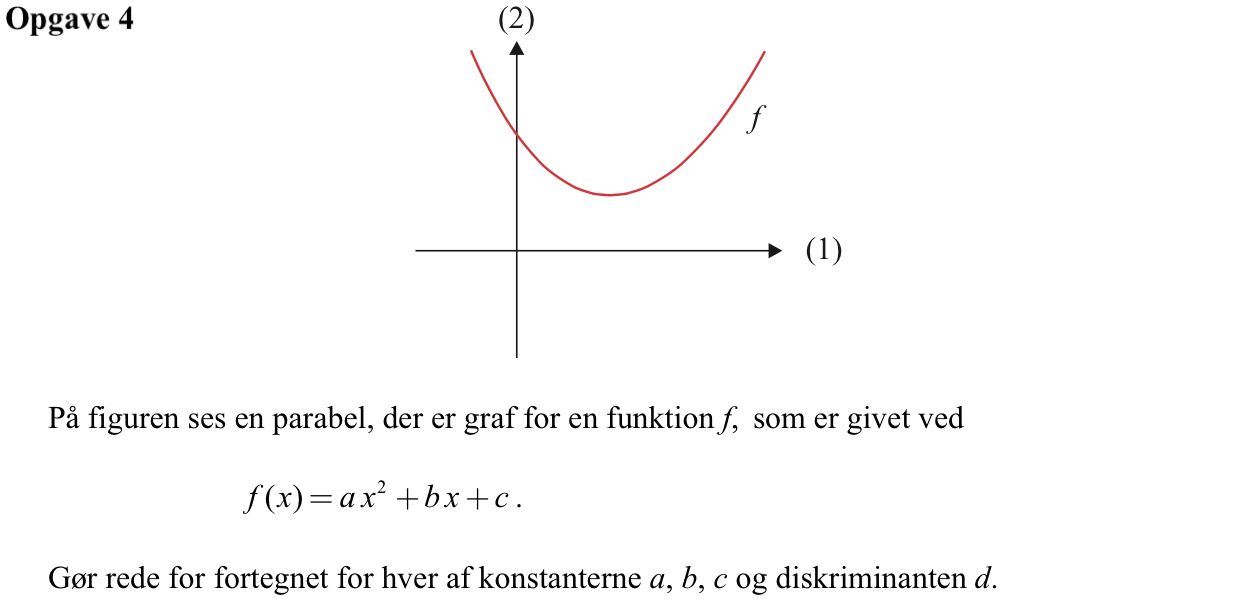
Svar på opgave 4:

1. Grenene på parablen vender opad, dvs. a > 0

   Parablens hældning i det punkt, hvor den skærer y-aksen er negativ, dvs. b < 0

   Parablen skærer y-aksens positive halvdel, dvs. c > 0

   Parablen skærer ikke x-aksen, dvs. diskriminanten, d < 0

Svar på opgave 5:

1. For en eksponentialfunktion gælder, at hver gang man lægger fordoblingskonstaten til x, så fordobles f(x). Tilsvarende: hver gang man trækker fordoblingskonstanten fra x, så halveres f(x). Det giver her: f(x + 3) = 2·f(x), henholdsvis f(x - 3) = (1/2)·f(x).

   I skemaet har man f(3) = 10. Ud fra dette skal man finde f(0). Man får: f(0) = f(3 - 3) = (1/2)·f(3) = (1/2)·10 = 5.

   Endelig skal man finde x, så f(x) = 40. Man har, at 40 = 4·f(3) = 2·2·f(3) = 2·f(3 + 3) = f(3 + 3 + 3) = f(9). Dvs. i det sidste tomme felt skal der stå x = 9. Det færdige resultat er vist nedenunder.

   

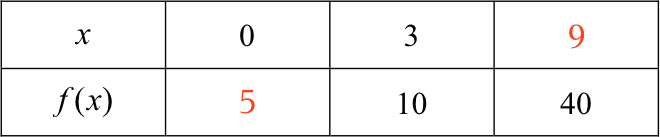
Svar på opgave 6:

1. Man skal lave en fortegnsundersøgelse for f´(x) og starter med at løse f´(x) = 0 med hensyn til x.

   f´(x) = x² - 4. f´(x) = 0 ⇒ x² - 4 = 0 ⇔ x = ±2.

   f´(-3) = 9 - 4 = 5 > 0

   f´(0) = -4 < 0

   f´(3) = 9 - 4 = 5 > 0

   Dvs. f vokser for x < -2, f aftager for -2 < x < 2 og f vokser for x > 2

Svar på opgave 7:

Løsning i Ti-Nspire.

1. Man opretter en liste med antal år efter 2004 og en liste med indtægter i mio. kr.:

   år:={2004,2005,2006,2007,2008}-2004 ▸ {0,1,2,3,4}

   indtægt:={310,350,424,515,582} ▸ {310,350,424,515,582}

   Man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... og vælger listerne, som man har oprettet. Man får følgende resultat:

   ExpReg år,indtægt,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",305.445]
   ["b",1.17892]
   ["r²",0.992546]
   ["r",0.996266]
   ["Resid","{...}"]["ResidTrans","{...}"]]

   (Bemærk at regressionsfunktionen gemmes som f1, og at Ti-Nspire bruger x i stedet for t).

   Heraf ses at a = 1,179 og b = 305,4, idet Ti-Nspire bruger a og b modsat opgaven.

   (Hvis man er i tvivl, kan man få Ti-Nspire til at udskrive f1(x): f1(x) ▸ 305.445*(1.17892)^x)

2. Den årlige indtægt i 2010 findes i Ti-Nspire:

   f1(2010-2004) ▸ 820.068

   Dvs. den årlige indtægt i 2010 i følge modellen er 820 mio. kr.

3. Den årlige vækstrate i % er (a - 1)·100 % = (1,179 - 1)·100 % = 17,9 %

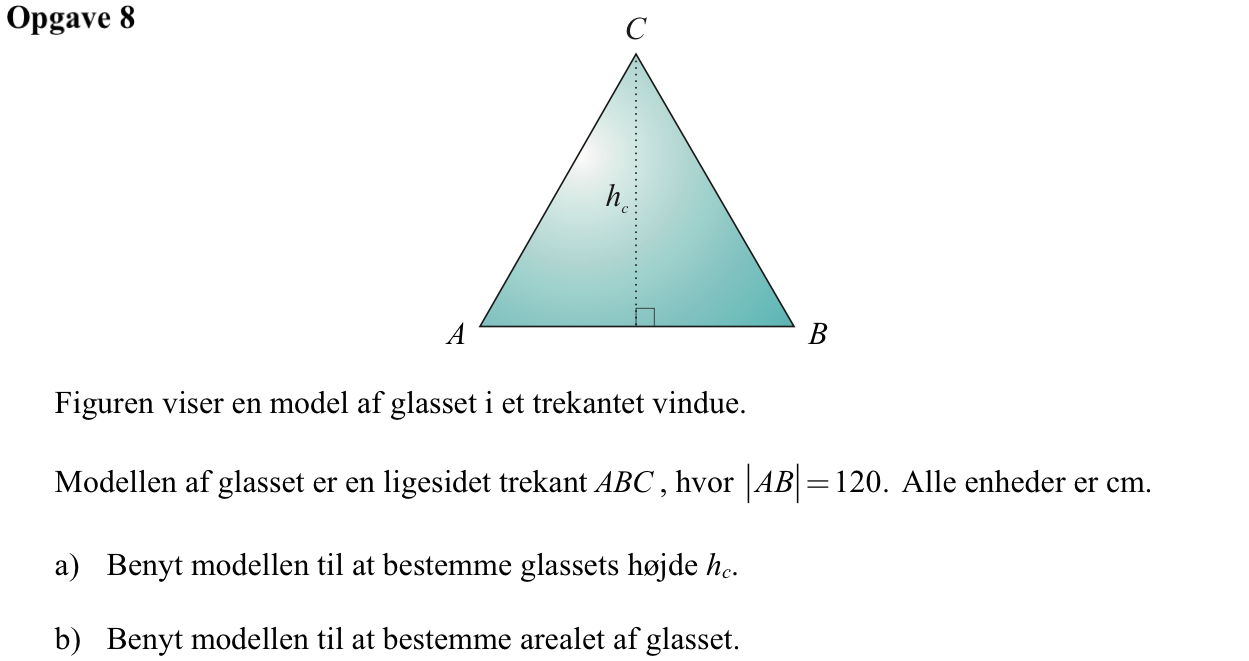
Svar på opgave 8:

1. I den ligesidede trekant ABC er |AC| = |AB| = 120 cm. |AD| = 60 cm. Højden findes som den længste katete i den retvinklede trekant ACD ved hjælp af Pythagoras læresætning.

   

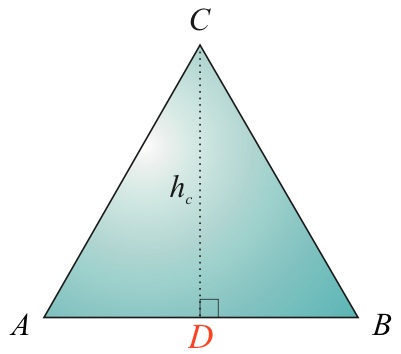
   Dette beregnes i Ti-Nspire: h:=sqrt(120²-60.²) ▸ 103.923

   Dvs. højden i C er 103,9 cm

2. Arealet er (1/2)·|AB|·h_c = (1/2)·120·103,923 cm² = 6235 cm²

Svar på opgave 9:

1. Funktionen f(x) oprettes i Ti-Nspire: f(x):=12246/(1+3.95*exp(−0.0273*x)) ▸ Udført

   Grafen for f er tegnet nedenunder i Ti-Nspire:

   

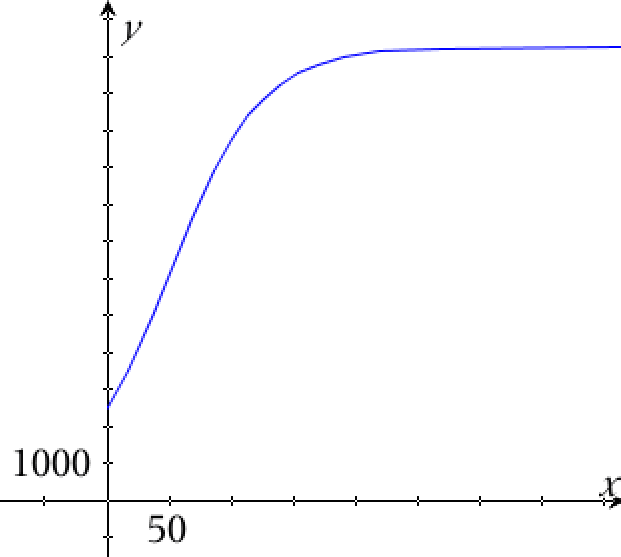
   Befolkningen i 2016 beregnes i Ti-Nspire: f(2016-1950) ▸ 7413.93. Dvs. befolkningen er 7413 mio. mennesker

2. f´(70) beregnes i Ti-Nspire: derivative(f(x),x)|x=70 ▸ 77.8259

   f´(70) fortæller, at i 2020 (1950 + 70 år) vil verdens befolkning vokse med 78 mio. mennesker på et år.

Svar på opgave 10:

1. Man opretter f(x) i Ti-Nspire: f(x):=(2-x)*ln(x) ▸ Udført

   Ligningen f(x) = 0 løses med hensyn til x i Ti-Nspire:

   solve(f(x)=0,x) ▸ x=1 or x=2

   Dvs. løsningerne er x = 1 og x = 2

2. Arealet af M er integralet af f fra x = 1 til x = 2. Dette beregnes i Ti-Nspire:

   integral(f(x),x,1.,2) ▸ 0.136294

   Dvs. arealet af M er 0,136

Svar på opgave 11:

1. Man opretter en liste for observerede antal i Ti-Nspire:

   observeret:={23,34,27,41,19,36,26,44} ▸ {23,34,27,41,19,36,26,44}

   Man opretter en liste for forventede antal, idet alle skal være en ottendedel af det samlede antal:

   forventet:={1,1,1,1,1,1,1,1}*(sum(observeret)/8.) ▸ {31.25,31.25,31.25,31.25,31.25,31.25,31.25,31.25}

   Man foretager en chi-i-anden goodness-of-fit test med 7 frihedsgrader på det observerede og det forventede antal. Man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ² Goodnes of Fit test...

   χ²GOF observeret,forventet,7: stat.results ▸
   [["Titel","χ²-Goodness of Fit test"]
   ["χ²",17.648]
   ["PVal",0.013663]
   ["df",7.]
   ["CompList","{...}"]]

   Det ses at PVal = 0,014 = 1,4 %. Da dette er mindre end 5 % forkastes nulhypotesen om, at alle udfald er lige sandsynlige.

Svar på opgave 12:

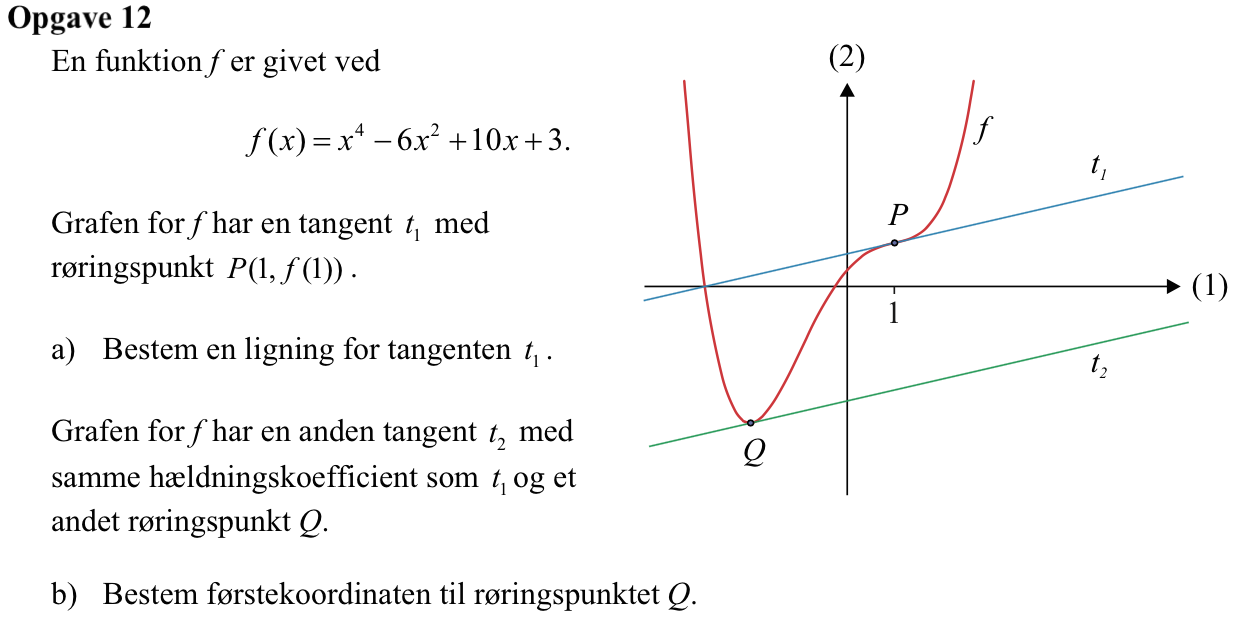
1. Man opretter f(x) i TI-Nspire:

   f(x):=x⁴-6*x²+10*x+3 ▸ Udført

   Tangentligningen findes ved hjælp af Ti-Nspire kommandoen tangentLine, som man sætter "y=" foran for at få hele ligningen skrevet på en gang:

   y=tangentLine(f(x),x,1) ▸ y=2*x+6

   Dvs. tangentens lignng er y = 2x + 6

2. Man skal finde x-værdien til det punkt på grafen for f ud over P, der har hældningen 2. Dette gøres i Ti-Nspire:

   solve(derivative(f(x),x)=2,x) ▸ x=−2 or x=1

   Dvs. førstekoordinaten for Q er -2

Svar på opgave 13:

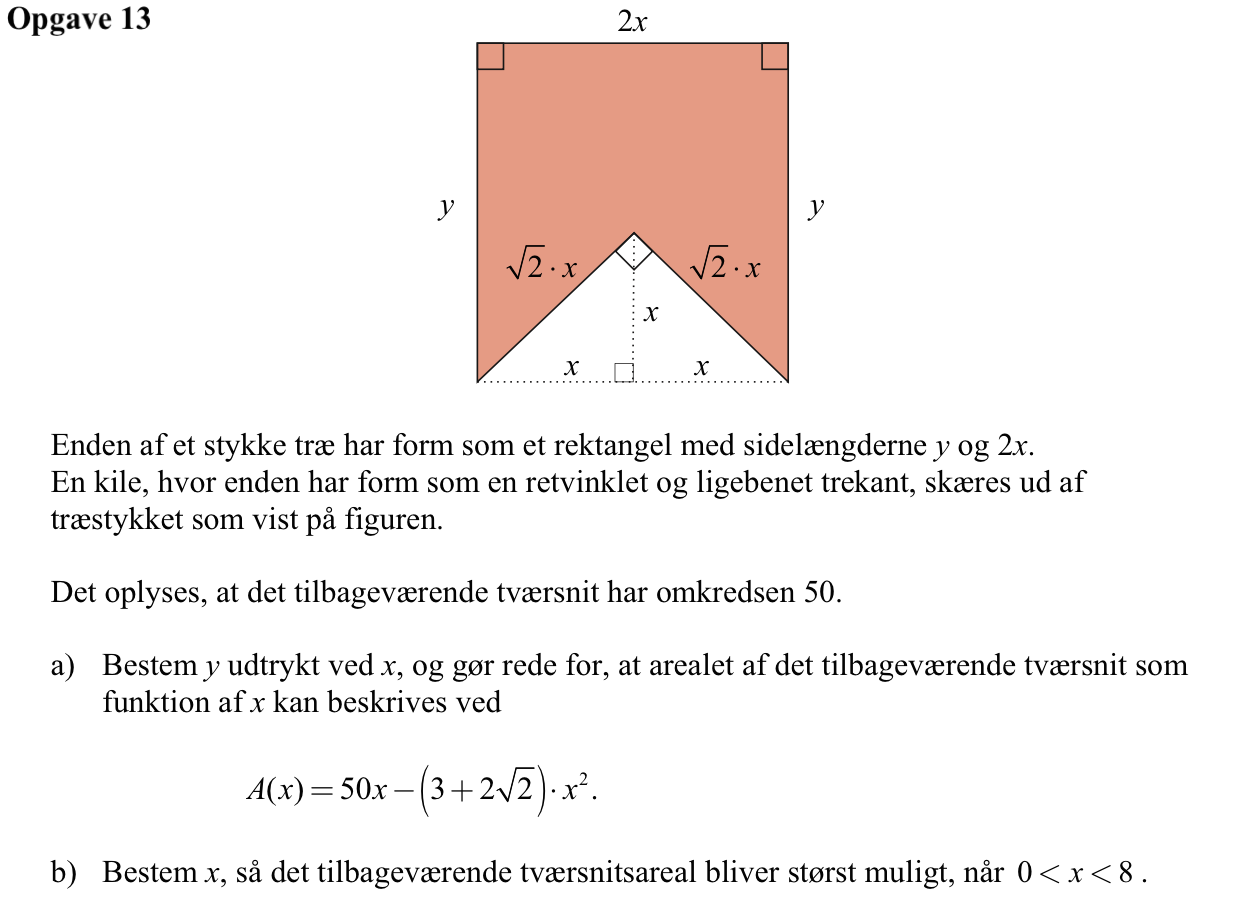
1. Omkredsen er 2x + y + √2·x + √2·x + y =

   2x + 2·√2·x + √2·x + y + y =

   (2 + 2·√2)·x + 2·y =

   2·x·(1 + √2) + 2·y.

   Dette skal være lig med 50. Det giver med hensyn til y:

   2·x·(1 + √2) + 2y = 50 ⇔ y = 25 - x·(1 + √2)

   Arealet er: arealet af firkant ABCD minus arealet af trekant ADE som vist:

   

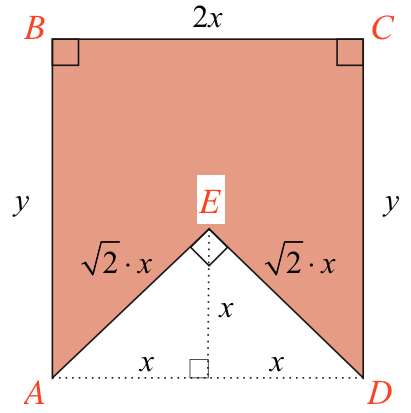
   Dette areal er 2·x·y - (1/2)·(2·x)·x = 2·x·(25 - x·(1 + √2)) - x² = 50x - 2·x² + 2·x·(√2) - x² =

   50x - 3·x² + 2·x²·√2 = 50x - (3 + 2√2)·x²

2. Man finder x-værdien for det størst mulige tværsnitsareal ved at løse ligningen A´(x) = 0 med hensyn til x. Herved finder man de x, hvor funktionen A har lokale ekstrema og vandrette vendetangenter. I dette tilfælde får man:

   A´(x) = 50 - (2·(√2 + 1))·x + 2·x·(-√2 - 1) - 2·x

   (Maple: diff(A(x),x); Ti-Nspire: derivative(A(x),x))

   Man løser ligningen A´(x) = 0: (kommandoen er fælles for Ti-Nspire og Maple)

   solve(50-(2*(√2+1))*x+2*x*(-√2-1)-2*x = 0., x) ▸ 4.28932

   Man finder A´(4) og A´(5):

   A´(4) = 50 - (2·(√2 + 1))·4 + 2·4·(-√2 - 1) - 2·4 = 3,37258

   A´(5) = 50 - (2·(√2 + 1))·5 + 2·5·(-√2 - 1) - 2·5 = −8,28427

   Det ses, at A'(x) er positiv før nulpunktet for A'(x) og negativ efter; dermed er x = 4,29 et maksimum.

   (I Maple kan maksimum og det x, der giver maksimum, findes med kommandoen: maximize(2.*x*(25-(sqrt(2)+1)*x)-x², location) → 107.23, {[{x = 4.2893}, 107.23]}. I Ti-Nspire kan x'et findes med kommandoen: fMax(2.*x*(25-(sqrt(2)+1)*x)-x²,x) ▸ x=4.2893)

   Dvs. det største tværsnitsareal fås for x = 4,29