Svar på opgave 1:

1. (a - b)² - b² = a² - 2ab + b² - b² = a² - 2ab

Svar på opgave 2:

1. 200 er antallet af dyr år 2002. 1,04 er fremskrivningsfaktoren (vækstraten plus 1). Den er det tal som antallet af dyr fra sidste år skal ganges med for at få dette års antal.

Svar på opgave 3:

1. En linje har ligningen y = a·x + b. Koefficienten a er hældning og findes her ud fra P og Q's koordinater: a = (12 - 3)/(5 - 2) = 3

   Man har nu: y = 3x + b. Her findes b ved at indsætte P's koordinater i lignigen: (3) = 3·(2) + b ⇒ b = 0.

   Dette giver ligningen : y = 3x

Svar på opgave 4:

1. Funktionen kan skrives f(x) = ax² + bx + c, hvor a = 3, b = -6 og c = 1.

   Formlen for toppunktet for en parabel med disse koefficienter er (x,y) = (-b/[2a],[c - b²/(4a)]) = (-[-6/(2·3)], 1 - [6²/(4·3)]) = (1,-2)

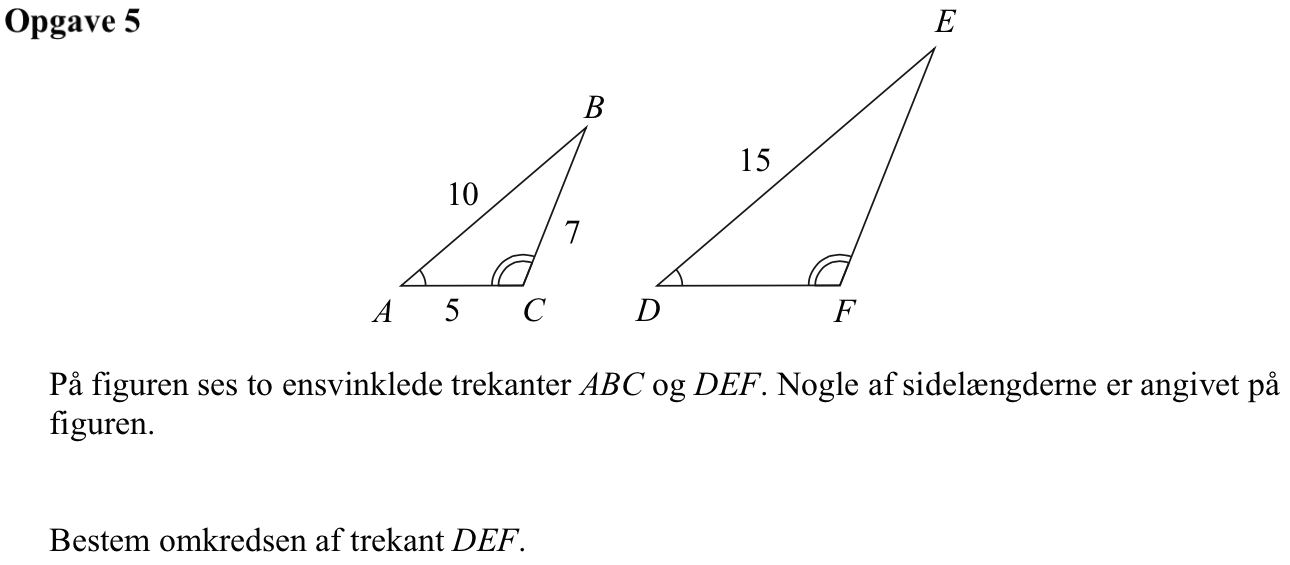
Svar på opgave 5:

1. Skaleringsfaktoren er 15/10 = 1,5. Dvs. omkredsen af trekant DEF er 1,5 gange omkredsen af trekant ABC = 1,5·(10 + 7 + 5) = 33

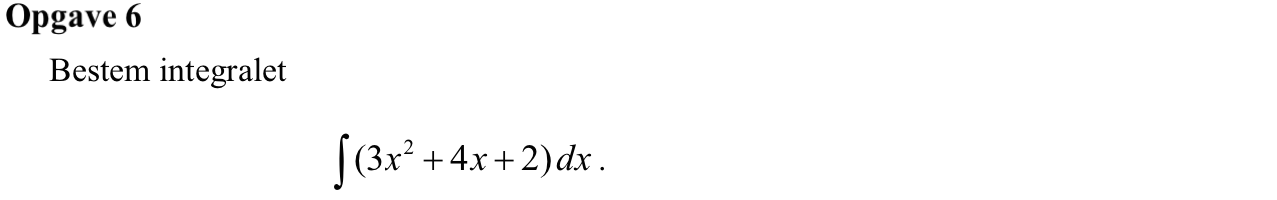
Svar på opgave 6:

1. Integralet af (3x² + 4x + 2) dx = 3·⅓x³ + 4·½x² + 2·x + k = x³ + 2x² + 2·x + k

Svar på opgave 7:

Løsning i Ti-Nspire.

1. Man opretter to lister: en for testtider og en for halvmaratontider.

   test_tider:={16,19,23,25,28,31,35} ▸ {16,19,23,25,28,31,35}

   halvmaraton:={76,87,107,119,139,160,202} ▸ {76,87,107,119,139,160,202}

   Man bruger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... og vælger listerne, som man har oprettet. Man får resultatet:

   

   Det ses af beregningen at a = 1,053 og b = 33,01

   Bemærk at Ti-Nspire bruger a og b omvendt af opgaven.

2. Den forventede løbetid i minutter for halvmarathon er f(30) = 33,01·1,053³⁰ = 154 minutter

Svar på opgave 8:

Løsning i Ti-Nspire.

1. Man får figuren:

   

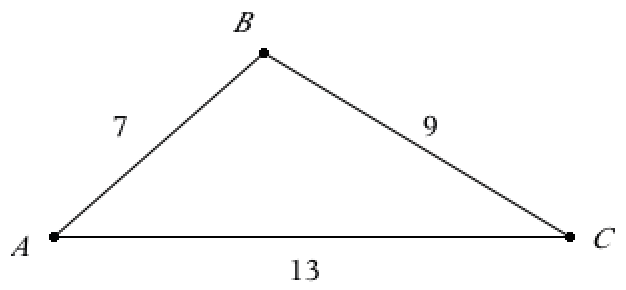
   Man sætter x = ∠A og bruger cosinusrelationen samt solve-kommandoen:

   solve(cos(x*1.°)=(13²+7²-9²)/(2*13*7),x)|0<x<180 ▸ x=41.17

2. Arealet af trekant ABC = 0,5·h·g = 0,5·h_B·|AC| = 0,5·[|AB|·sin(41,17°)]·13 =

   0,5·[7·sin(41,17°)]·13 = 30,0

   Som vist er højden fra B til b også kaldet h_B = [7·sin(41,17°)] = 4,61

Svar på opgave 9:

1. Vægten af kloen er K = 0,036·400^1,356 mg = 121,5 mg

   Vægten af krabben er M = (53/0,036)^(1/1,356) mg = 216,9 mg

2. Procentvækst for potensfunktion: ((1 + 30%)^1,356 - 1)·100% = 42,7 %

Svar på opgave 10:

1. Man bruger Ti-Nspire kommandoen: y=tangentLine(3*ln(x+1)-x²,x,0) ▸ y=3*x

   Dvs. tangentligningen er y = 3x

2. Man skal lave en fortegnsundersøgelse for f´(x). Man bruger Ti-Nspire kommandoerne:

   solve(derivative(3*ln(x+1)-x²,x)>0.,x)|x>−1 ▸ −1.<x<0.82288 og

   solve(derivative(3*ln(x+1)-x²,x)<0.,x)|x>−1 ▸ x>0.82288

   Første linje viser, at f´(x) > 0 for −1 < x < 0,82288, og at f´(x) < 0 for x > 0,82288.

   Dvs. f(x) vokser for -1 < x < 0,823 og aftager for x > 0,823. X = 0,823 er et maksimum.

Svar på opgave 11:

Løsning i Ti-Nspire.

1. Man indtaster 0.0038*x⁴-0.42*x³+12.12*x²+24.13*x+16.67|0≤x≤52 på graf-modulets kommandolinje og får:

   

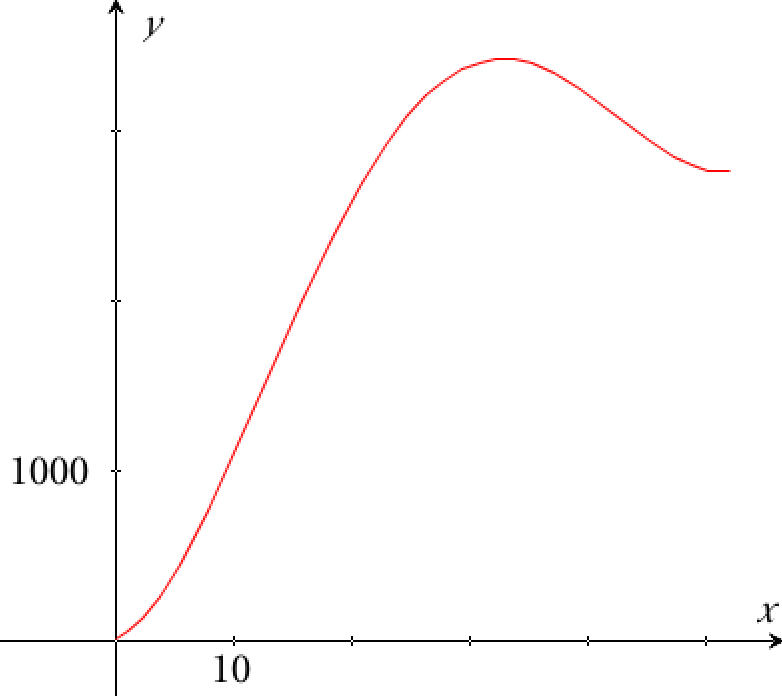
   Bemærk: x bruges til at tegne grafen i stedet for t.

2. Man bruger fMax()-kommandoen i Ti-Nspire:

   fMax(0.0038*t⁴-0.42*t³+12.12*t²+24.13*t+16.67,t)|0≤t≤52 ▸ t=32.80

   Dermed er alderen, hvor hunkalkunen opnår sin største vægt 32,8 uger.

   (Hvis man bruger endepunkts- og ekstremumsundersøgelse, så får man et lokalt maksimum ved 32,8 og et lokalt minimum ved 51,0. Her er det lokale maksimum svaret på spørgsmålet, da begge endepunkter har lavere funktionsværdier.)

3. f´(10) findes i Ti-Nspire:

   derivative(0.0038*t⁴-0.42*t³+12.12*t²+24.13*t+16.67,t)|t=10 ▸ 155.73

   Dette tal viser, at hunkalkunerne vokser med 156 gram om ugen efter netop 10 uger.

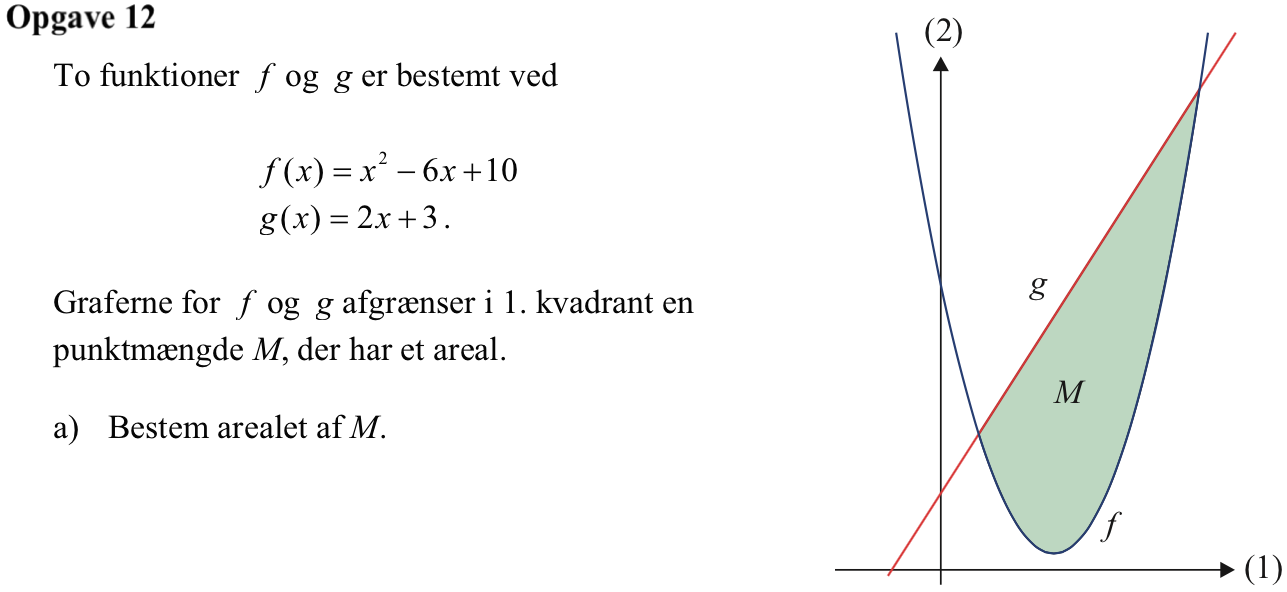
Svar på opgave 12:

1. Man skal bestemme skæringspunkterne for f og g og derefter integrere g - f for x liggende i intervallet mellem skæringspunkterne.

   Løsning i Ti-Nspire:

   

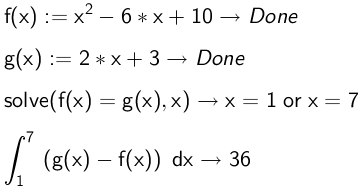
   Dvs. arealet af M er 36

Svar på opgave 13:

Løsning i Ti-Nspire.

1. Der er tale om goodness-of-fit.

   Nulhypotese: Den observerede fordeling af kernetyper følger den forventede fordeling

2. Man opretter to lister som vist nedenunder: en kaldet observeret, der indeholder observerede hyppigheder og en kaldet forventet, der indeholder forventede hyppigheder.

   observeret:={648,237,195,63} ▸ {648,237,195,63} (liste over observationer)

   sum(observeret) ▸ 1143 (samlet antal observationer)

   forventet:=1143.*{9/16,3/16,3/16,1/16} ▸ {642.938,214.313,214.313,71.4375} (liste for forventet hyppighed)

   Man analyserer de fundne data med kommandoen

   χ²GOF observeret,forventet,3: stat.results,

   der findes under værktøjs-menuen (når man er i Noter):

   Beregninger ▸ Statistik ▸ Statistiske tests ▸ χ²-Goodness of Fit test...

   Man vælger de oprettede lister, skiver antallet af frihedsgrader = 3 og får:

   

   PVal er sandsynligheden for, at teststørrelsens værdi skyldes tilfældigheder.

   Nulhypotesen accepteres fordi PVal = 0,159 = 15,9 % og dermed større end 5%.