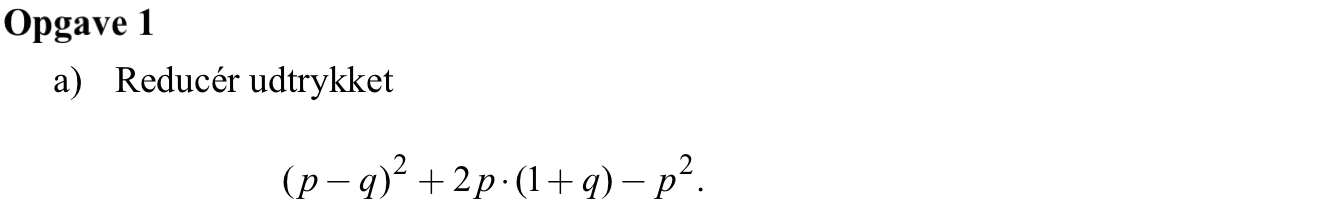
Svar på opgave 1:

1. (p - q)² + 2·p·(1 + q) - p² = p² - 2·p·q + q² + 2·p + 2·p·q - p² = 2·p + q²

Svar på opgave 2:

1. Arealet af parallelogrammet er den numeriske værdi af determinanten af vektorerne a og b, som udspænder det. Dvs. arealet = |det(a,b)| = |2·8 - 3·6| = 2

2. Idet X = (x, y) er et punkt på linjen, og idet â er tværvektor til a, får man linjens ligningen ved: â·PX = 0 ⇒ (-3,2)·(1-x,5-y) = 0 ⇒ -3·(1-x) + 2·(5-y) = 0 ⇒ 3x - 2y + 7 = 0

Svar på opgave 3:

1. P(x) = ax² + bx + c, hvor der her gælder, at a = 3, b = 6 og c = 10.

   Toppunktet = (-b/(2·a), c - b²/(4·a)) = (-6/(2·3),10-36/4·3) = (1,7)

Svar på opgave 4:

1. Der er tale om eksponentiel positiv vækst. Startværdien er 1523 og fremskrivningsfaktoren er 1 + 4% = 1,04. x er antal år efter 2015 og f(x) er antallet af biler. Man får modellen:

   f(x) = 1523·1,04^x, x > 0

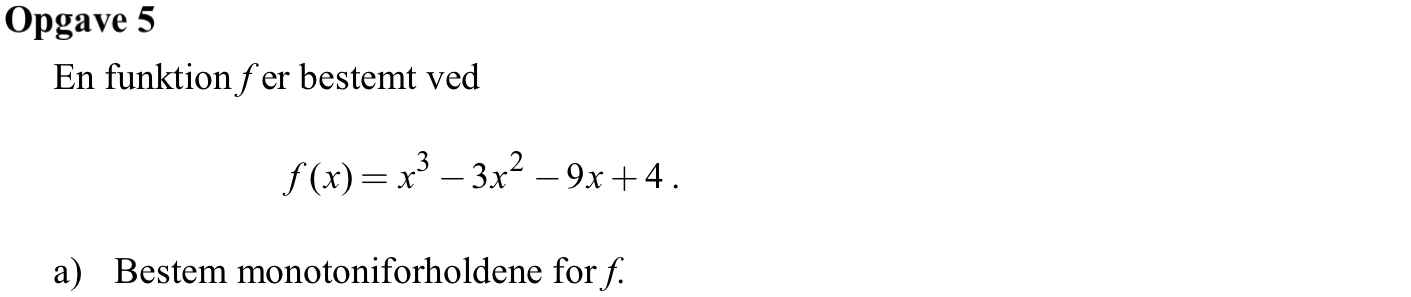
Svar på opgave 5:

1. f´(x) = 3x² - 6x -9.

   Nulpunkterne for f´(x) er x = -1 og x = 3. Da f´(x) er en parabel, der vender grenen opad vil f´(x) være positiv for x < -1, negativ for -1 < x < 3 og positiv for 3 < x. Man får monotoniforholdene

   f(x) vokser for x < -1, aftager for -1 < x < 3 og vokser for 3 < x

Svar på opgave 6:

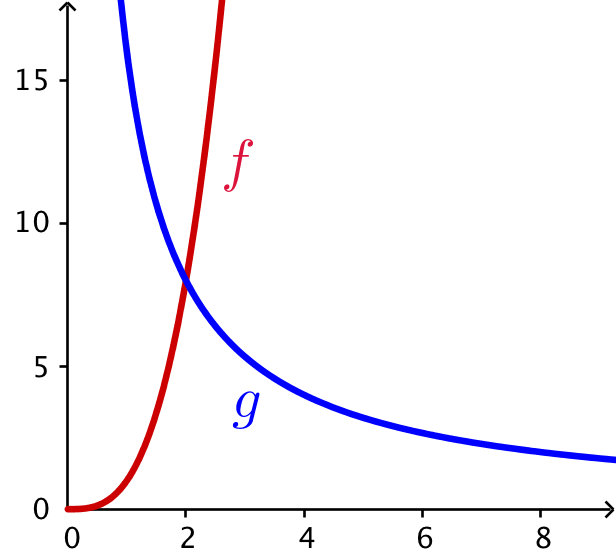
1. f(2) = 2³ = 8, g(2) = 16/2 = 8

   Grafer tegnet i Geogebra:

   

Svar på opgave 7:

1. En vilkårlig stamfunktionen til f(x), er det ubestemte integrale til f(x), som er lig med x⁴ + 2·e^3x + 7x + k.

   For den stamfunktion F(x), som man leder efter, gælder: F(0) = 8 ⇒ 0⁴ + 2·e^3·0 + 7·0 + k = 8 ⇒ 2 + k = 8 ⇒ k = 6. Man får:

   F(x) = x⁴ + 2·e^3x + 7x + 6

Svar på opgave 8:

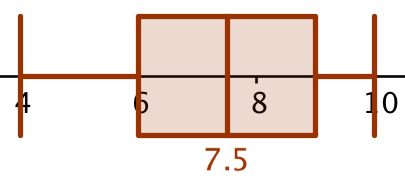
1. Man laver tabellens tal om til ugrupperede data ved at skrive hvert smerteniveau det antal gange som hyppigheden angiver. De ugrupperede data stilles op i nummerorden og inddeles i 4 lige store dele evt. med et tal som skillelinje:

   4 5 5 5 5 6 6 6 7 7 7 7 7 7 7 | 8 8 8 8 8 9 9 9 9 9 9 9 9 10 10. Man ser, at

   minimum = 4, 1. kvartil = 6, medianen = 7,5, 3. kvartil = 9 og maksimum = 10

   Boksplot tegnet i Geogebra:

   

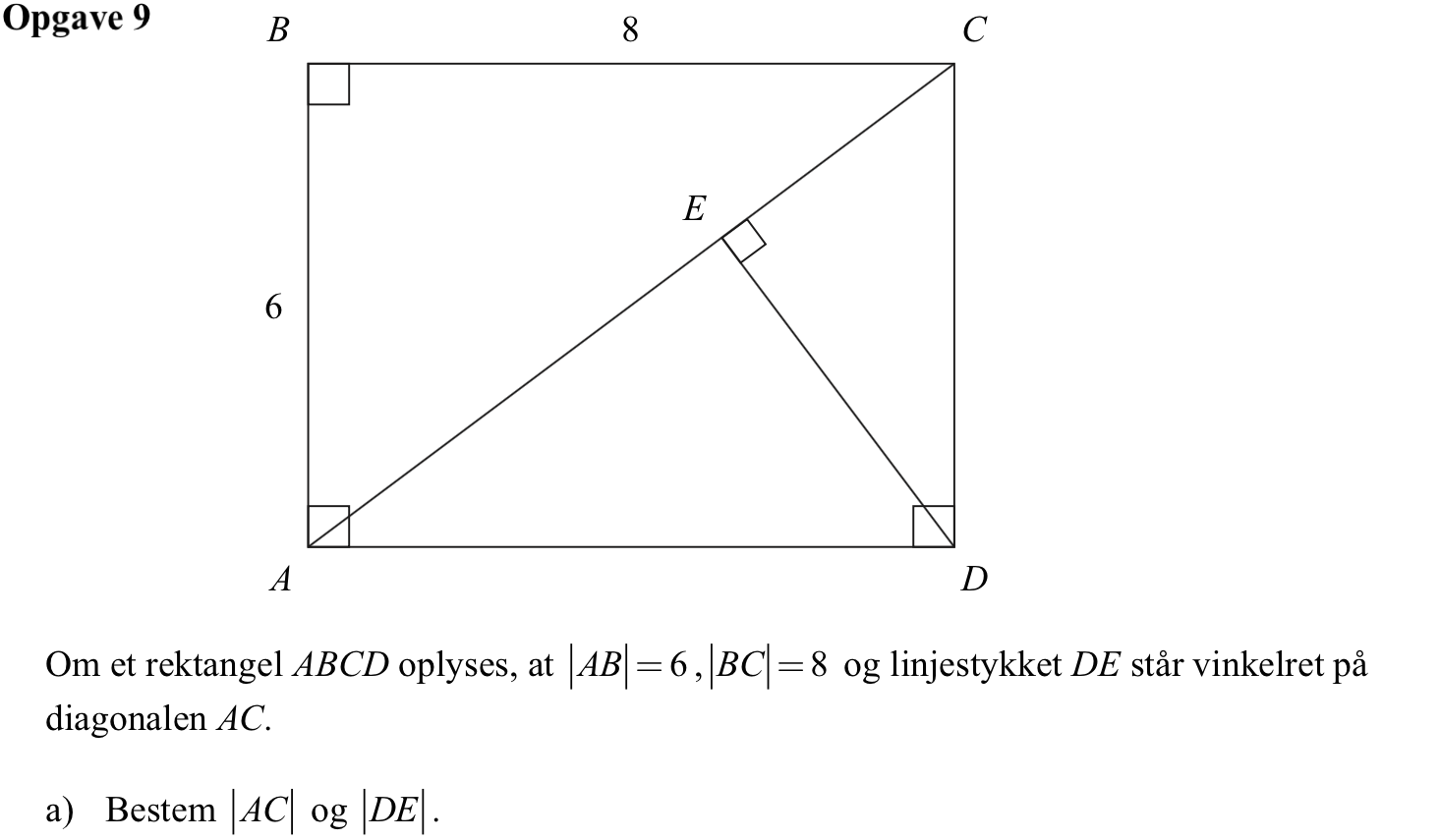
Svar på opgave 9:

1. |AC| findes ved hjælp af Pythagoras læresætning: |AC|² = |AB|² + |BC|² ⇒ |AC| = √[6² + 8²] = 10

   Trekanterne ABC og CDE er ensvinklede. Skaleringsfaktoren er forholdet mellem hypotenuserne i de to trekanter = 6/10 = 0,6. |DE| = 8·0,6 = 4,8

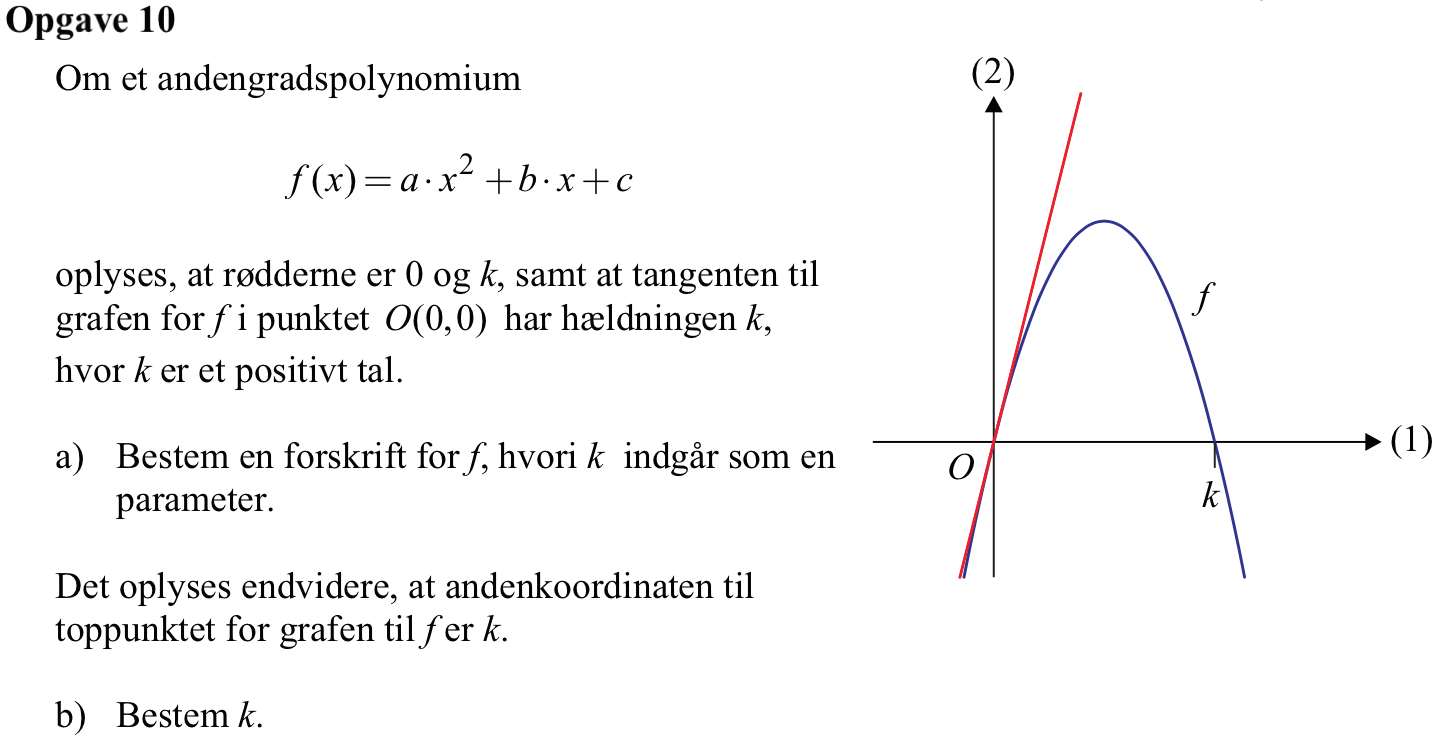
Svar på opgave 10:

1. Da grafen går gennem (0,0) er c = 0, idet c = f(0).

   Koefficienten b er hældningen af funktionen til x = 0 og dermed er b = k.

   Der gælder endvidere, at f(x) = a·x·(x - k) = ax² - a·k·x, idet f's rødder er 0 og k. Man har nu f(x) = ax² + k·x = ax² - a·k·x ⇒ a = -1.

   Dermed er f(x) = -x² + k·x

2. Y-værdien af toppunktet har formlen: c - b²/(4·a) = -k²/(4·(-1)) = k²/4. Dette skal være lig med 4. Dette giver:

   k²/4 = k ⇒ k = 4, idet k er positivt

Svar på opgave 11:

1. Løsning i Ti-Nspire: Man opretter to lister:

   tykkelse:={0.4,1.2,2.3,3.9,4.8,7.7,7.9,8.9} ▸ {0.4,1.2,2.3,3.9,4.8,7.7,7.9,8.9}

   laengde:={4.8,13.7,24.5,26.6,40,54.6,44.8,57.8} ▸ {4.8,13.7,24.5,26.6,40,54.6,44.8,57.8}

   Man bruger kommandoen: Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potensregression... på listerne x=tykkelse og y=laengde og får:

   

   Heraf ses, idet man bytter om på a og b fra resultatet, at a = 0.765 og b = 10.86

2. Procentvis forøgelse: (1,10^0.765 - 1)·100% = 7,6%

3. Man sammensætter udtrykkene i Ti-Nspire og får: m:=0.001943*(10.86*x^0.7653)^3.276 ▸ 4.80675*(x^0.7653)^3.276.

   Eksponenterne ganges sammen og man får: M = 4,807·x^2.507

   Man skal løse M(x) = 2500 og får i Ti-Nspire:

   solve(m(x)=2500,x) ▸ x=12.1157

   Dvs. tykkelsen af lårbensknoglen er 12,1 cm

Svar på opgave 12: Sfærisk geometri

1. På en enhedskugle er buelængder lig med centervinklen mellem buens endepunkter målt i radianer. Man kan også bruge grader for buelængder, så længe man er på en enhedskugle.

   ∠A kaldes va, ∠B kaldes vb og ∠C kaldes vc.

   Man opretter de kendte værdier omregnet til radianer i Ti-Nspire:

   va:=(30/180)*π*1. ▸ 0.523599

   b:=(45/180)*π*1. ▸ 0.785398

   c:=(113/180)*π*1. ▸ 1.97222

   Man finder resten ved hjælp af cosinusrelationerne og opretter om nødvendigt værdierne i CAS efterhånden som man finder dem:

   solve(cos(a)=cos(b)*cos(c)+sin(b)*sin(c)*cos(va),a)|a>0 and a<π ▸ a=1.27928

   a:=1.27928 ▸ 1.27928

   solve(cos(b)=cos(a)*cos(c)+sin(a)*sin(c)*cos(vb),vb)|vb>0 and vb<π ▸ vb=0.378066

   vb:=0.378066 ▸ 0.378066

   solve(cos(c)=cos(a)*cos(b)+sin(a)*sin(b)*cos(vc),vc)|vc>0 and vc<π ▸ vc=2.64034

   Man får, at

   a = 1,279·(180°/π) = 73,2°

   ∠B = 0,3781·(180°/π) = 21,7°

   ∠C = 2,640·(180°/π) = 151,3°

2. Arealet er ∠A + ∠B + ∠C - π = 0,5236 + 0,3781 + 2,640 - π = 0,400

Løsning i Geogebra:

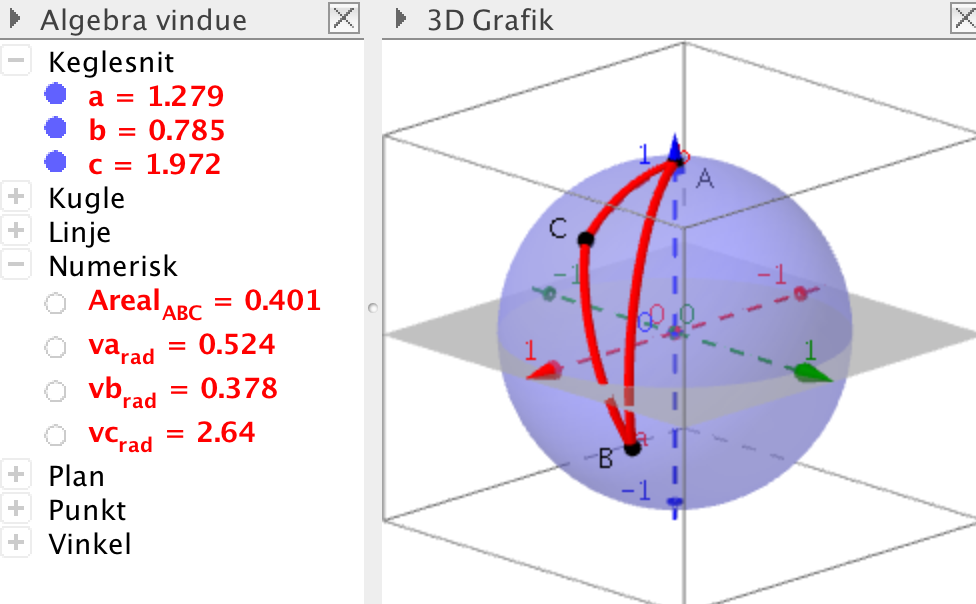
Prøv at dreje figuren på Geogebras hjemmeside

Svar på opgave 13:

1. Nulhypotesen er at afvigelser fra det forventede skyldes tilfældigheder.

   Man opretter to lister i Ti-Nspire: en med oberserverede værdier og en med forventede.

   observeret:={18,32,47,60,71,88,65,51,38,19,11} ▸ {18,32,47,60,71,88,65,51,38,19,11}

   forventet:=1.*sum(observeret)*{(1/36),(2/36),(3/36),(4/36),(5/36),(6/36),(5/36),(4/36),(3/36),(2/26),(1/36)} ▸ {13.89,27.78,41.67,55.56,69.44,83.33,69.44,55.56,41.67,38.46,13.89}

   Man udfører følgende kommando på de to lister og sætter antallet af frihedsgrader til 10:

   Beregninger ▸ Statistik ▸ Statistiske tests ▸ Χ²-Goodness of Fit test... og får:

   

   PVal = 0,15 er sandsynligheden for at teststørrelsens værdi skyldes tilfældigheder. Da PVal er større end 5% accepteres nulhypotesen.

Svar på opgave 14:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=x⁴-8*x³+16*x²+x+5 ▸ Udført

   Man bruger Ti-Nspire kommandoen y=tangentLine(f(x),x,4) ▸ y=x+5

   Dvs. tangentens ligning er y = x + 5

2. Man skal beregne integralet af |f(x) - g(x)| mellem skæringspunkterne for de to funktioner. Man får følgende i Ti-Nspire:

   g(x):=x+5 ▸ Udført

   solve(f(x)=g(x),x) ▸ x=0 or x=4 (skæringspunkter)

   

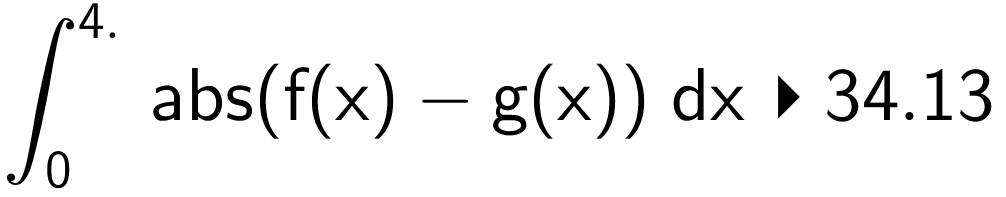
   Dvs. arealet af M er 34,13

3. Volumenet er π gange den numeriske værdi af integralet af [f(x)]² minus integralet af [g(x)]² begge taget fra x = 0 til x = 4. I Ti-Nspire giver det:

   

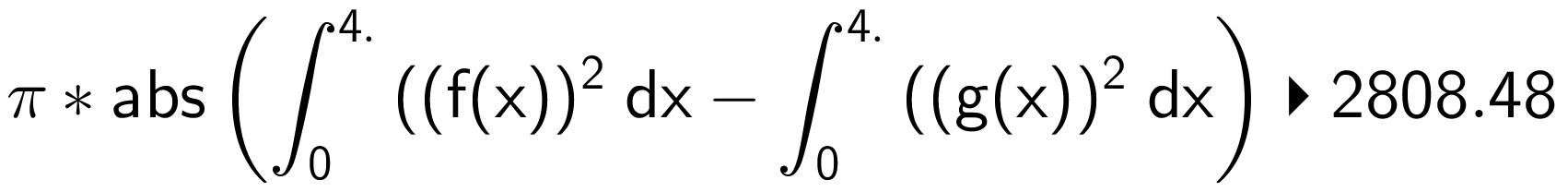
   Dvs. volumenet af omdrejningslegemet er 2808

Svar på opgave 15:

1. r(t) er en stedvektor. Man skal vise at |r(t)| = 5 for alle t. Man får:

   |r(t)| = √[t² + 1 + (24 - t²)] = √[25] = 5 hvilket dermed er bevist.

2. Sporet for r(t) er integralet af længden af r'(t) fra t = -4 til t = 4.

   r'(t) = (1,0,-t/√[24-t²]). |r'(t)| = √[1 + t²/(24-t²)]. Man får i Ti-Nspire:

   

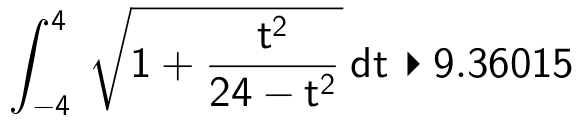
   Længden af sporet er 9,36

Svar på opgave 16:

1. Man bruger desolve() kommandoen i Ti-Nspire:

   deSolve(t'=0.3*(20-t)+15*e^−0.3*x and t(0)=15,x,t)|0≤x≤50 ▸

   t=20.*(0.740818^x)*(1.34986^x+0.75*(x-0.33333)) and 0≤x≤50

   Dvs. forskriften er: T = 20·0,741^x·[1,350^x + 0,75·(x - 0,333)], 0 ≤ x ≤ 50

2. Man bruger fMax() kommandoen i Ti-Nspire:

   fMax(20.*(0.740818^x)*(1.34986^x+0.75*(x-0.33333)),x)|0≤x≤50 ▸ x=3.66667

   Dvs. tidspunktet for den største temperatur er 3,67 timer efter start.