Svar på opgave 1:

1. Variable: x er antallet af år efter 2001, y er antallet af slædehunde. Der er tale om en aftagende lineær sammenhæng: y = a·x + b, hvor a er et negativt tal. b = y(0) = 21.365. a = -1.135.

   Modellen bliver: y = -1.135·x + 21.365, hvor 0 ≤ x ≤10.

Svar på opgave 2:

1. Man skal løse ligningen a·b = 0 med hensyn til t. Man får:

   

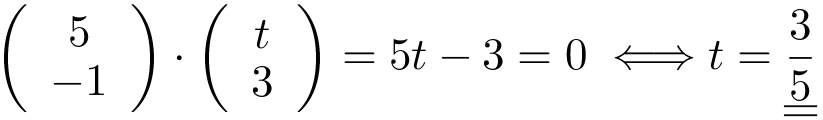
Svar på opgave 3:

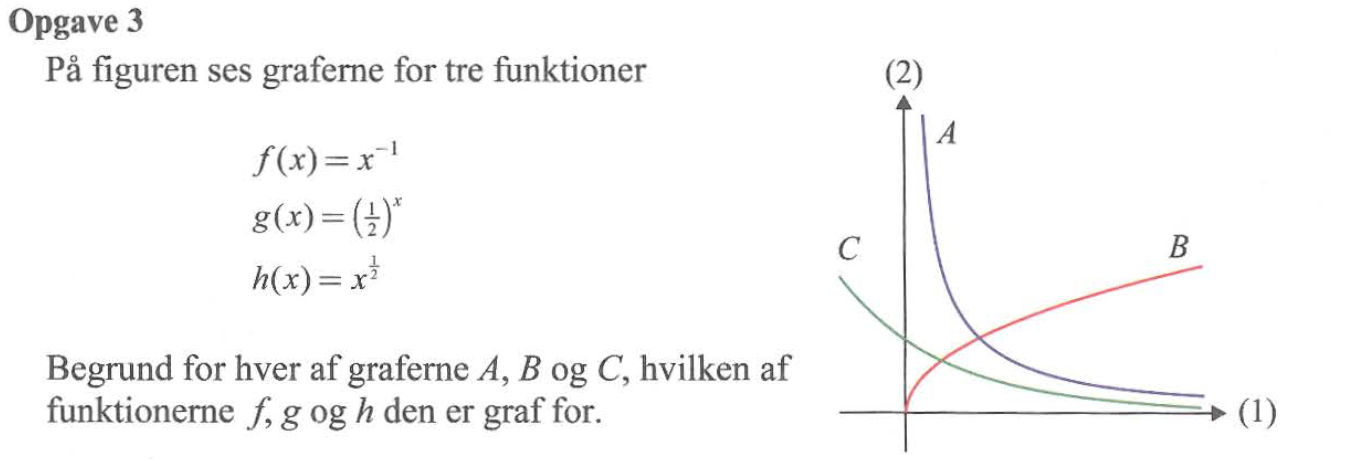
1. f(x) er en potensfunktion med negativ eksponent. Den går mod uendelig for x gående mod nul og mod nul for x gående mod uendelig. Det passer med A.

   g(x) er en eksponentialfunktion med et grundtal, der er mindre end 1. Den går mod nul for x gående mod uendelig og mod uendelig for x gående mod minus uendelig. For x = 0 er den lig med 1. Det passer med C.

   h(x) er en postensfunktion med en eksponent, der ligger mellem 0 og 1. Den går mod uendelig for x gående mod uendelig, idet funktionens vækst bliver langsommere og langsommere. Det passer med B.

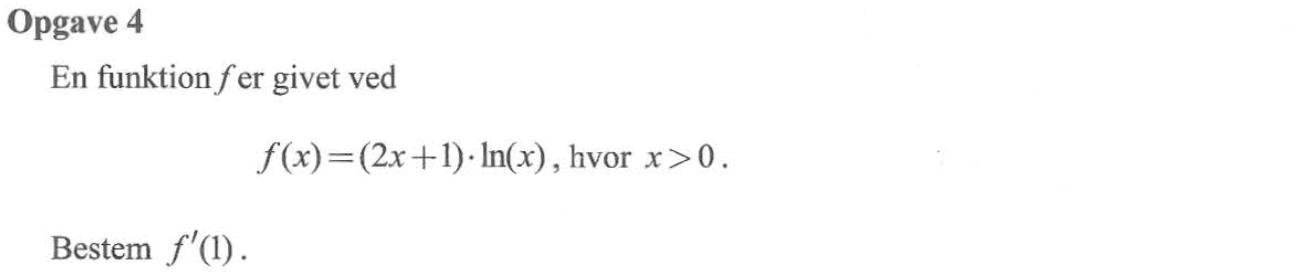
Svar på opgave 4:

1. f'(x) = [(2x + 1)·ln(x)]' = (2x + 1)·(1/x) + 2·ln(x) = (2 + 1/x) + 2·ln(x)

Svar på opgave 5:

1. (Man behøver ikke at løse differentialligningen).

   Tangenten til f gennem P = (0,3) har ligningen:

   y = f'(0)·(x - 0) + 3 ⇔ y = (exp(0) + 2·3)·(x - 0) + 3 ⇔ y = (1 + 6)·(x - 0) + 3 ⇔ y = 7x + 3

Svar på opgave 6:

1. x-værdien til toppunktet er -b/(2·a). Da dette er lig med 5, får man: -b/(2·a) = 5 ⇒ b = -10·a. Dette giver: f(x) = a·x² - 10·a + 21.

   Man ved ud fra punktet A = (3,0), at f(3) = 0 og får: f(3) = 0 ⇒ a·3² - 10·a·3 + 21 = 0 ⇒ -21·a + 21 = 0 ⇒ a = 1. Dette giver: b = -10.

   Dermed er a = 1 og b = -10

   Desuden ved man, at nulpunkter for f ligger symmetrisk omkring x-værdien for toppunktet, som er 5. Dvs. det andet nulpunkt må være x = 7 og dermed er B = (7,0)

Svar på opgave 7:

1. Løsning af nulpunkt i Ti-Nspire:

   

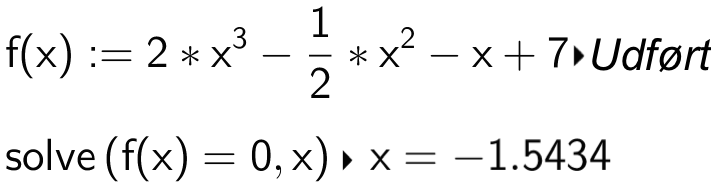
   Koordinatsættet bliver: P = (-1,54 ; 0)

2. Beregning i Ti-Nspire af f´(x):

   

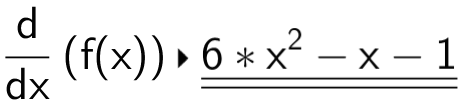
   Man bruger følgende kommando i Ti-Nspire: y=tangentLine(f(x),x,3) ▸ y=21*x-23.

   Dvs. tangenten er y = 21x - 23

3. Man skal beregne fortegns-intervaller for f´(x). Ti-Nspire:

   

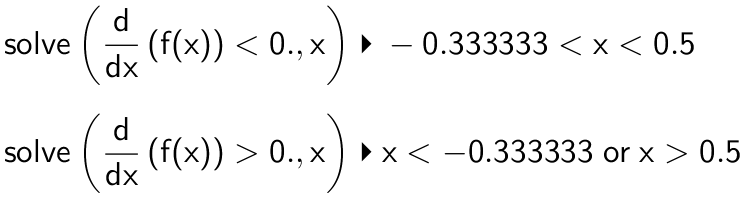
   Dermed er f voksende for x < -1/3, aftagende for -1/3 < x < 1/2 og voksende for x > 1/2

Svar på opgave 8:

1. Tegnet i Geogebra:

   

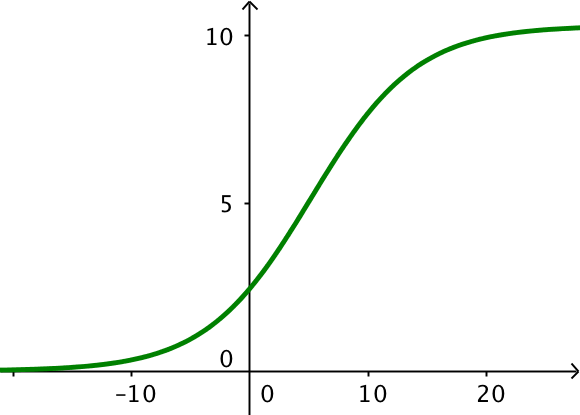
   Man skal løse ligningen v(x) = 8,5 med hensyn til x. I geogebra kaldes funktionen f(x), som defineres ved at skrive funktionsudtrykket for v(x) i input-feltet og trykke enter. Man får:

   

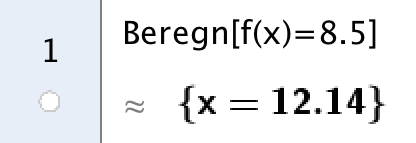
   Alderen er 12,1 år

2. Man skal løse ligningen v''(x) = 0 med hensyn til x. I Geogebra får man (idet v(x) kaldes f(x)):

   

   Man får, at den største væksthastighed findes ved alderen 5,2 år, hvilket stemmer med, at kurven har størst hældning omkring x = 5.

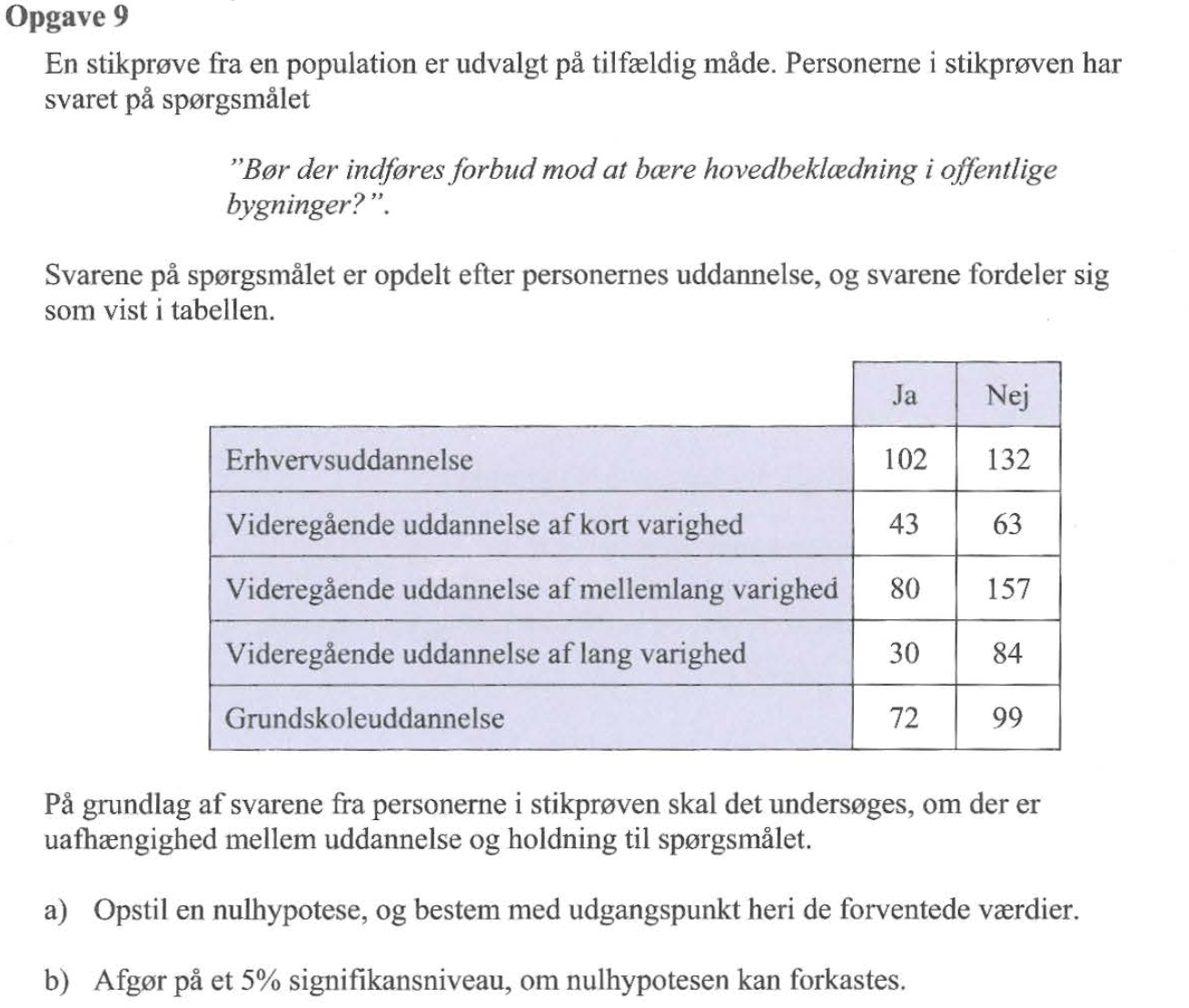
Svar på opgave 9:

Løsning i Ti-Nspire.

Der er tale om en uafhængighedstest.

De observerede værdier skrives ind i en matrix kaldet svar.



Man vælger kommandoen:

Beregninger ▸ Statistik ▸ Statistiske test ▸ Χ²-uafhængighedstest...,

vælger matricens navn på listen over matricer og får:



1. Nulhypotesen er, at holdningen til tørklæder er uafhængig af uddannelse

   De forventede værdier findes ved kommandoen:

   

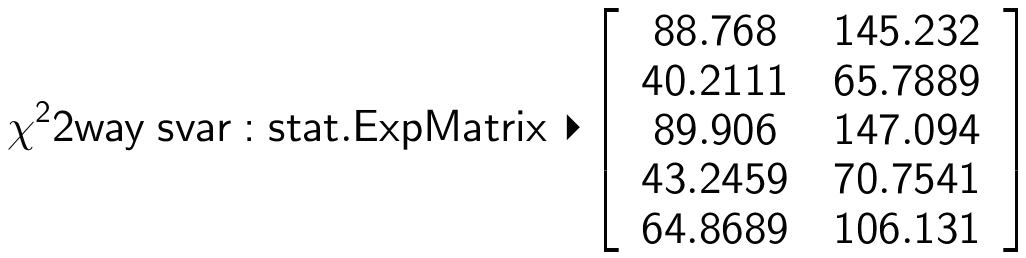
2. Da PVal (sandsynligheden for at afvigelser mellem observerede og forventede værdier skyldes tilfældighed) er mindre end 0,05, forkastes hypotesen

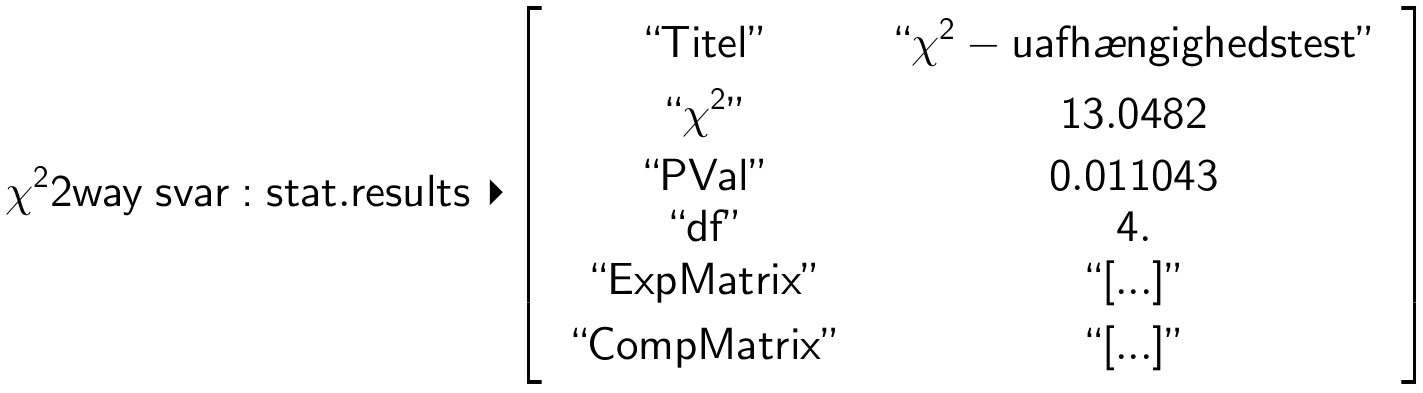
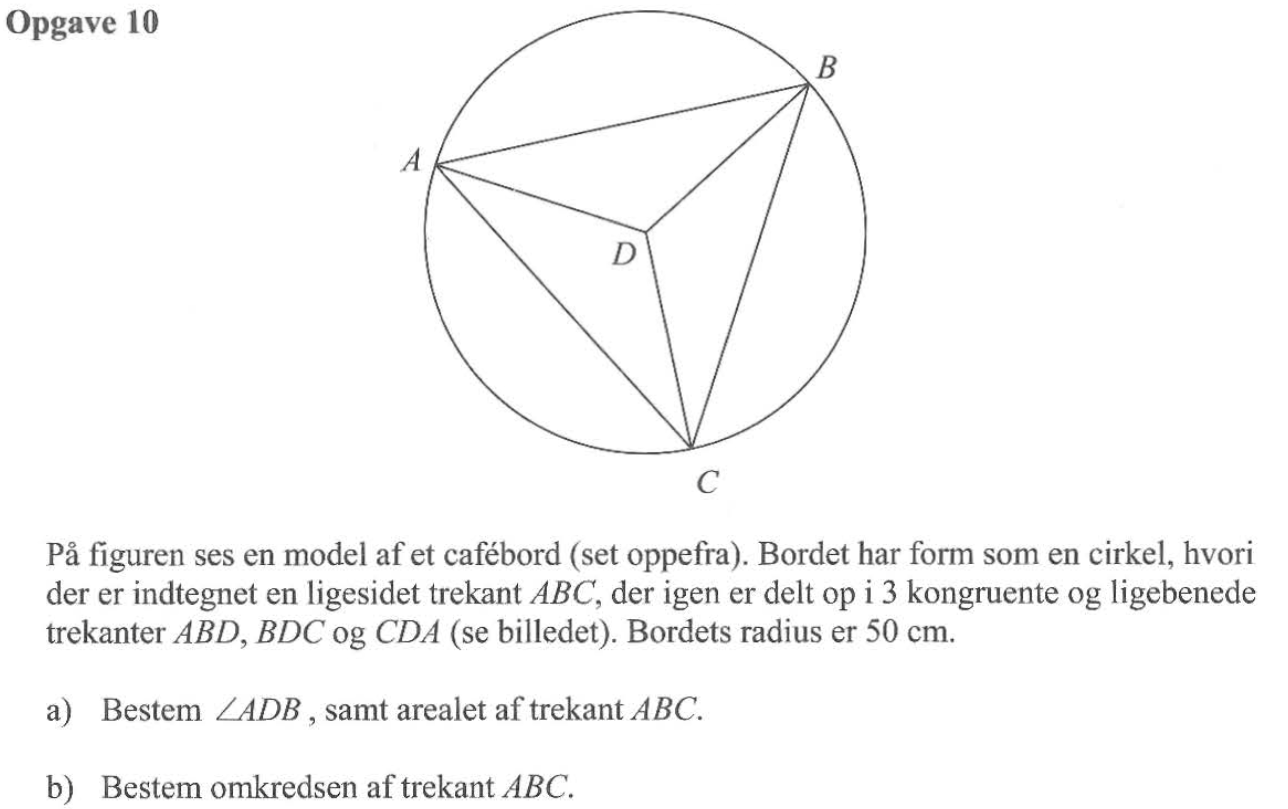
Svar på opgave 10:

1. Vinkel ADB er 120°, da den udspænder en tredjedel af cirklen.

   For en ligesidet trekant med siden s gælder:

   Areal = (√3)·s²/4

   Omkreds = 3·s

   s er korden i en cirkel og den udspændes af en vinkel på 120°.

   Formlen for sammenhængen mellem korden s og vinklen v er:

   s = 2·r·sin(v/2) = 2·50·sin(120°/2) = 25·sin(60°) = 25·(√3).

   Dette giver arealet: (√3)·[25·(√3)]²/4 cm² = 3.248 cm²

2. Omkredsen er 3·s = 3·25·(√3) = 260 cm

Svar på opgave 11:

Løsning i Ti-Nspire.

1. Man opretter to lister: en med antal år efter 2001 og en med den relative væksthastighed for hvert år.

   aarefter2001:={2001-2001,2002-2001,2003-2001,2004-2001,2005-2001,2006-2001} ▸ {0,1,2,3,4,5}

   relativhast:={0.398,0.302,0.259,0.221,0.158,0.124} ▸ {0.398,0.302,0.259,0.221,0.158,0.124}

   Man bruger kommandoen:

   Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Eksponentiel regression... og vælger listerne, som man har oprettet. Man får resultatet:

   

   Det ses af beregningen at a = 0.797 og b = 0.399

   Bemærk at Ti-Nspire bruger a og b modsat opgaven.

2. Man skal løse ligningen f(t) = 0,1 med hensyn til t. Man bruger solve()-kommandoen:

   solve(0.399*0.797^x=0.1,x) ▸ x=6.0987

   Der går: 6,1 år før den relative væksthastighed er nede på 0,1/år

   Halveringstiden = ln(1/2)/ln(a) = -0,693/(-0,227) = 3,1 år

3. Man skal løse diffrentialligningen: (1/N)·(dN/dt) = 0,399·0,797^t med startbetingelsen N(0) = 520.

   Løsning i Ti-Nspire:

   

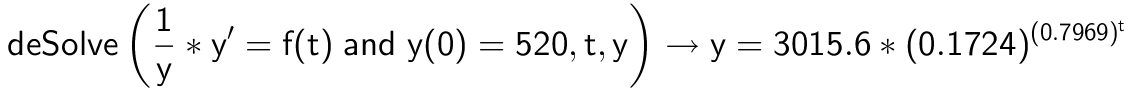
   Grafen giver:

   

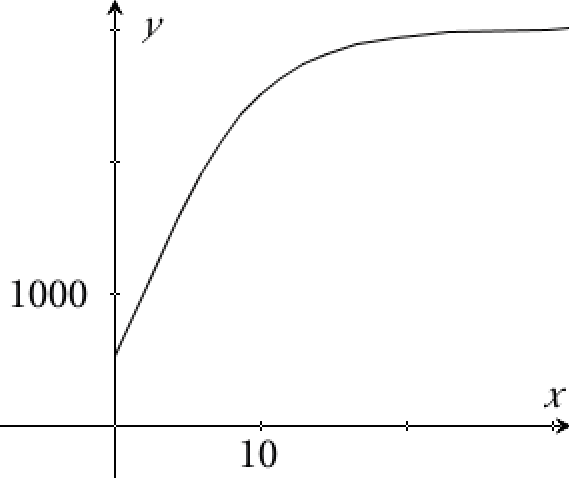
   Man skal løse ligningen N(t) = 2000 med hensyn til t. Man får:

   solve(3015.6*(0.1724)^0.7969t=2000,t) ▸ t=6.405

   Man undersøger f(6) og f(7) for at se hvilken der er den rigtige:

   f(6) ▸ 1922.4

   f(7) ▸ 2106.5

   Man når op over 2000 fisk efter 7 år, dvs. i 2008.

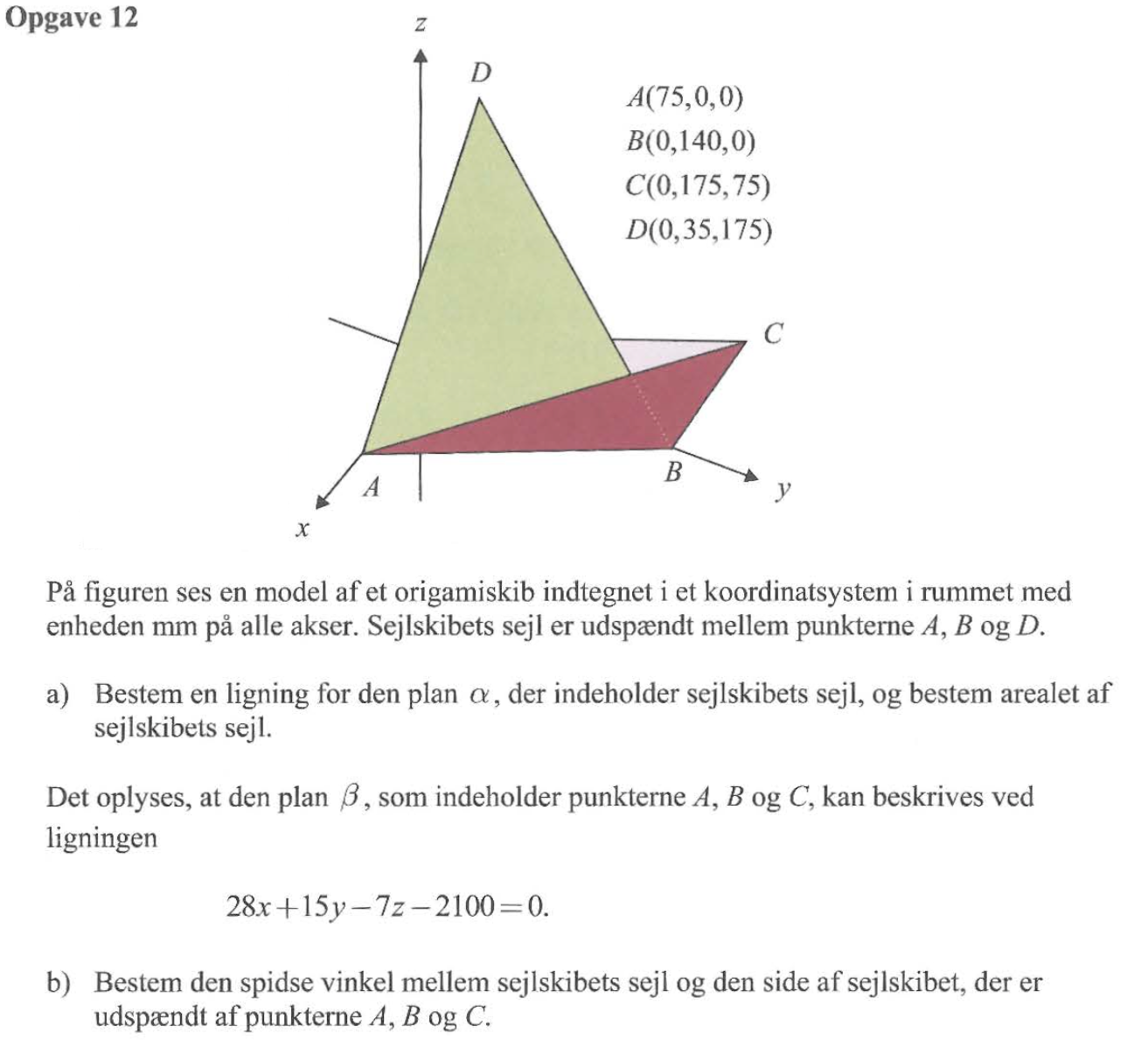
Svar på opgave 12:

Løsning i Geogebra.

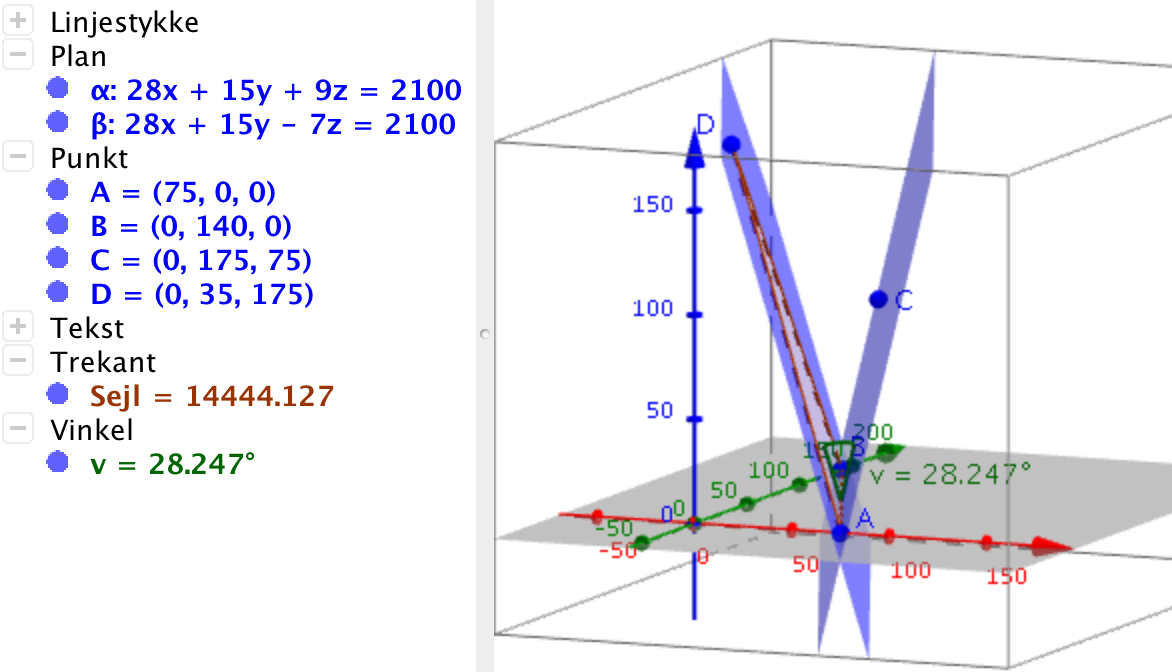
1. Ligningen for α aflæses til 28x + 15y + 9z - 2100 = 0

   Arealet af sejlet aflæses til 14.444

2. Vinklen mellem planerne er 28,2°

Løsning i Ti-Nspire.

1. Først defineres punkterne A-D (som vektorer) samt vektorerne AB og AD:

   a:=[75,0,0] ▸ [75,0,0]

   b:=[0,140,0] ▸ [0,140,0]

   c:=[0,,175,75] ▸ [0,175,75]

   d:=[0,35,175] ▸ [0,35,175]

   ab:=b-a ▸ [-75,140,0]

   ad:=d-a ▸ [-75,35,175]

   Man beregner krydsproduktet af AB og AD:

   crossP(ab,ad) ▸ [24500,13125,7875]

   Man dividerer igennem med 875, som er største fælles divisor for koordinaterne, og får normalvektoren

   nvektor:=[24500,13125,7875]/875 ▸ [28,15,9]

   Planens ligning findes af ligningen: nvektor · AX = 0. Her er X = (x, y, z) et punkt i planen. Man får:

   dotP([28,15,9],[75-x,0-y,0-z])=0 ▸ −28*x-15*y-9*z+2100=0

   Udtrykket ganges igennem med -1 (for få mindst muligt antal minustegn) og man får planens ligning:

   28x + 15y + 9z - 2100 = 0

   Arealet er halvdelen af længden af krydsproduktet AB×AD:

   0.5*norm([24500,13125,7875]) ▸ 14444

   Dvs. arealet af sejlet er 14.444

2. Vinklen beregnes som vinklen mellem planernes normalvektorer. Planen β har normal-vektoren: (28, 15, -7), hvilket aflæses af koefficienterne i β's ligning. Man bruger kommandoen:

   

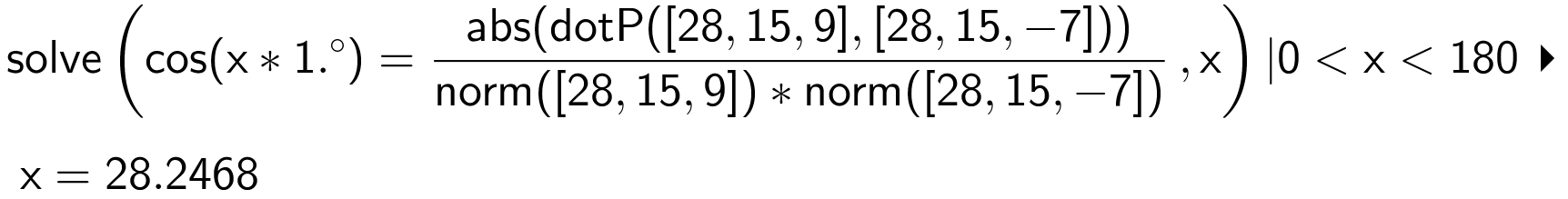
   Ved at tage den numeriske værdi i tælleren sikrer man sig, at det er den mindste vinkel, som man får. Ved at gange x med 1.0° sikrer man sig, at resultatet kommer ud som decimaltal og i grader.

   Vinklen er 28,2°

Svar på opgave 13:

1. Der er to sider med arealet 10·h, to sider med arealet 10·b og to endeflader med arealet h·b. I alt før man overfladearealet:

   O = 2·b·h + 20·h + 20·b

2. V = 100 ⇒ 20·b·h/3 = 100 ⇒ h = 30/(2·b). Dette indsættes i ovenstående funktion og man får: o(b) = 20·b + 300/b + 30.

   For at finde det mindst mulige overfladeareal, definerer man O(b) i Ti-Nspire og bruger fMin() kommandoen...:

   o(b):=20*b+300/b+30.|b>0 ▸ Udført

   fMin(o(b),b) ▸ b=3.87298

   Den værdi af b, der gør overfladearealet mindst muligt, er derfor 3,87 m

Svar på opgave 14:

Løsning i Ti-Nspire.

1. Man får grafen:

   

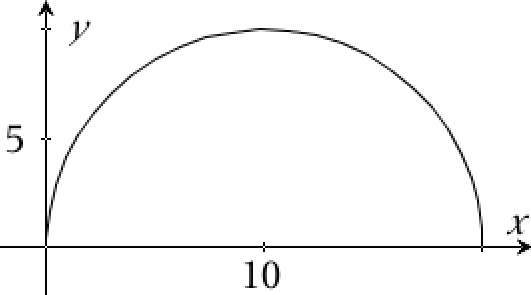
   X-værdien for det bredeste sted findes ved kommandoen:

   fMax(sqrt(−x²+20*x),x) ▸ 10

   Diameteren på det breddeste sted er 2·f(10) = 2·√[-(10)² + 20·10] = 20

   Diameteren ved åbningen er 2·f(18) = 12

2. Man finder det h, som giver overfladearealet 1005:

   

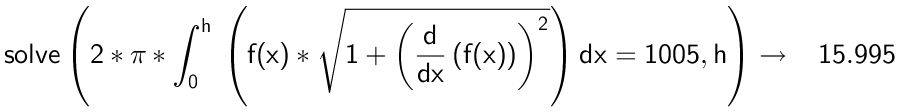
   Højden er 16,0

3. Man ved, at kuglens radius er 10, og at centrum ligger på x-aksen dvs. i punktet: (10,0,0). Dens ligning bliver:

   (x - 10)² + y² + z² = 10²