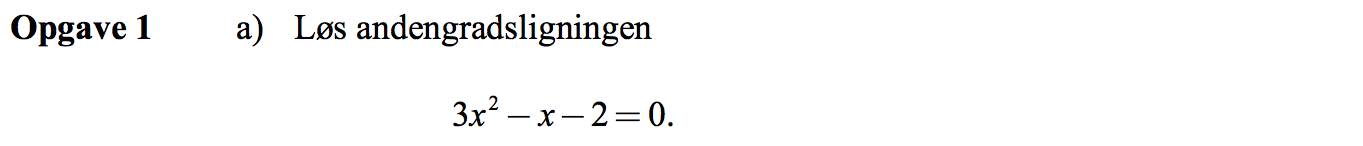
Svar på opgave 1:

1. 3x² - x - 2 = 0 ⇔

   x = 1/6 ± (1/6)√[1 + 4·3·2] ⇔

   x = 1/6 ± (1/6)√25 ⇔

   x = 1/6 ± 5/6 ⇔

   x = 1/6 - 5/6 ∨ x = 1/6 + 5/6 ⇔

   x = -2/3 ∨ x = 1

Svar på opgave 2:

1. Projektionen af a på b er:

   (a·b/|b|²)·b =

   ((5,1)·(-1,1)/|(-1,1)|²)·(-1,1) =

   ((5,1)·(-1,1)/(-1,1)²)·(-1,1) =

   ((-5 + 1)/(1 + 1))·(-1,1) =

   ((-4)/2)·(-1,1) =

   (-2)·(-1,1) =

   (2,-2)

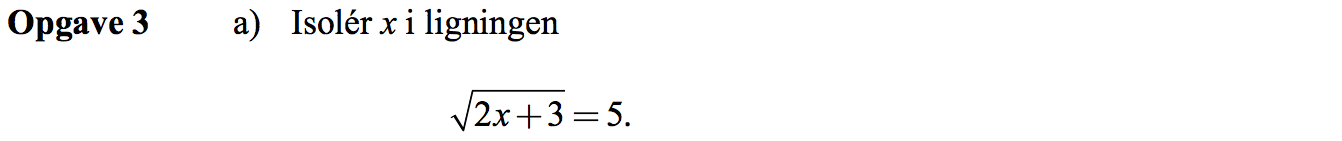
Svar på opgave 3:

1. √[2x + 3] = 5 ⇔

   2x + 3 = 5² ⇔

   2x + 3 = 25 ⇔

   2x = 25 - 3⇔

   2x = 22 ⇔

   x = 22/2 ⇔

   x = 11

Svar på opgave 4:

1. 250 er startværdien, dvs. massen af radioaktivt stof til tiden 0.

   0,9956 er fremskrivningsfaktoren, dvs. det tal man skal gange den gamle masse med hvert sekund for at få den nye masse.

Svar på opgave 5:

1. Vektoren AB er en retningsvektor for linjen l, der desuden går gennem punktet A = (-1,2).

   AB = (5,26) - (−1,2) = (6,24). Denne forenklen ved at dividere igennem med 6, dvs. som retningsvektor vælges AB/6 = (1,4)

   Dermed er parameterfremstillingen for l: (x,y) = (-1,2) + t·(1,4), hvor t er et reelt tal.

   Retningsvektoren for l er normalvektor for m, da de to linjer står vinkelret på hinanden.

   Antag at punktet P = (x,y) ligger på linjen m. Da vil der gælde, at skalarproduktet af vektor AP og AB er lig med nul.

   AP = (x,y) - (-1,2) = (x+1,y-2).

   Dette giver følgende ligning for linjen m:

   AP·AB = 0 ⇒

   (x+1,y-2)·(1,4) = 0 ⇔

   (x+1)·1 + (y-2)·4 = 0 ⇔

   x + 1 + 4y - 8 = 0 ⇔

   x + 4y - 7 = 0

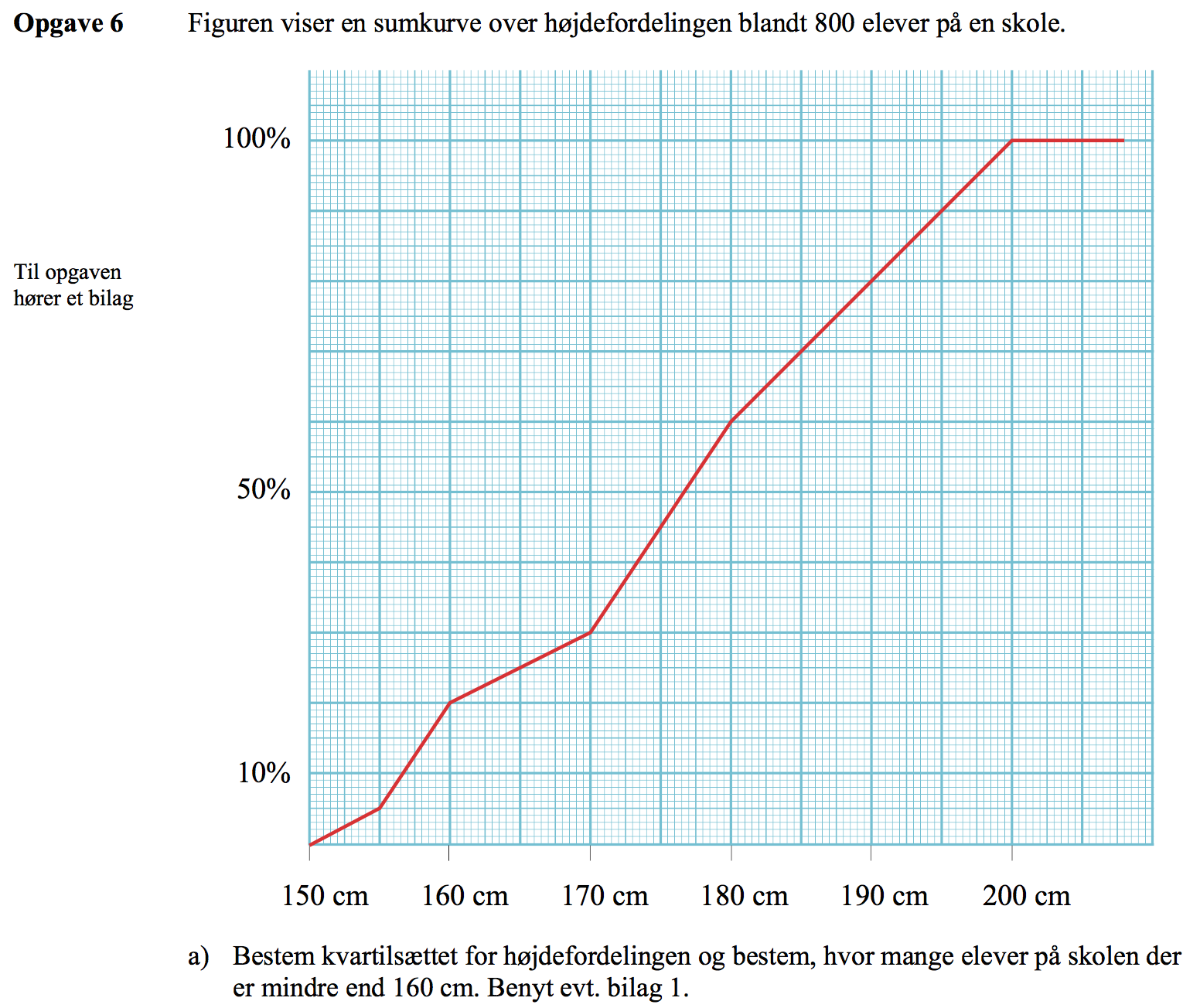
Svar på opgave 6:

1. Kvartilsættet findes som de værdier, der svarer til y-værdierne: 25%, 50% og 75%. Dette er vist nedenunder.

   

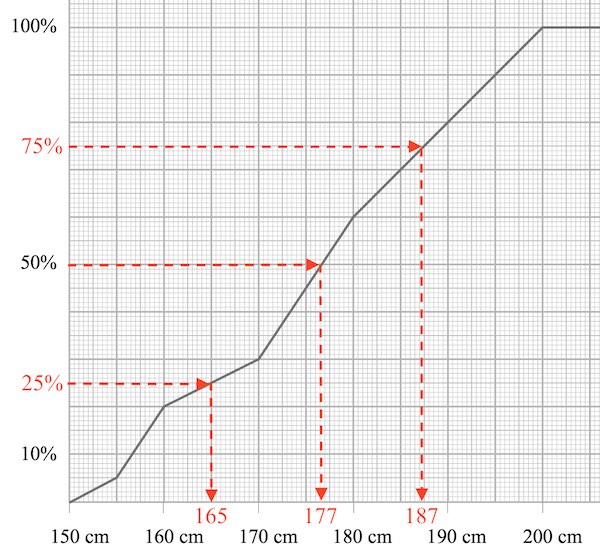
   Man ser at kvartilsættet aflæses til:

   Nedre eller første kvartil = 165 cm

   Median eller anden kvartil = 177 cm

   Øvre eller tredje kvartil = 187 cm

   Anden-aksen viser hvor mange procent af eleverne, der er under den højde, der aflæses på x-aksen. I dette tilfælde aflæses procentdelen af elever, der er under 160 cm, som vist nedenunder.

   

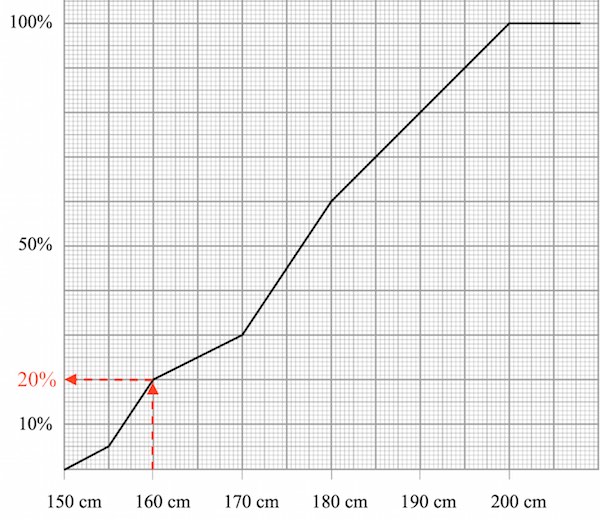
   Dvs. procentdelen af elever, der er under 160 cm, er 20 %

Svar på opgave 7:

1. Man finder først den afledede af f.

   f´(x) = 36x² - 48x + 12

   Tangentens ligning er y = f´(0)·(x - 0) + f(0).

   f(0) = 12·0³ - 24·0² + 12·0 = 0

   f´(0) = 36·0² - 48·0 + 12 = 12.

   Dvs. tangentens ligninge gennem punktet (0,f(0)) er y = 12·(x - 0) + 0 ⇔ y = 12x

2. Arealet af M er integralet af f fra x = 0 til x = 1.

   

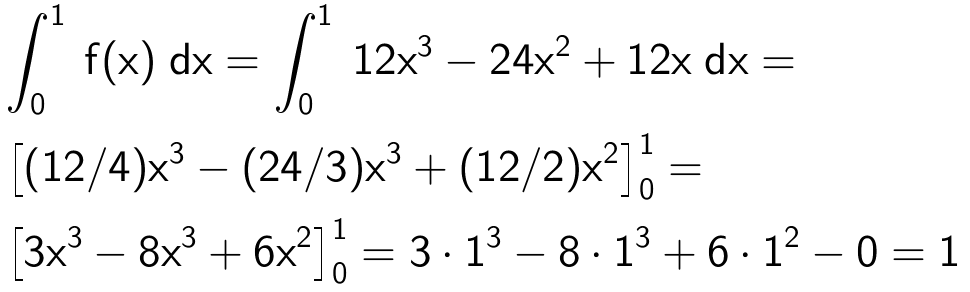
   Dvs. arealet af M er 1

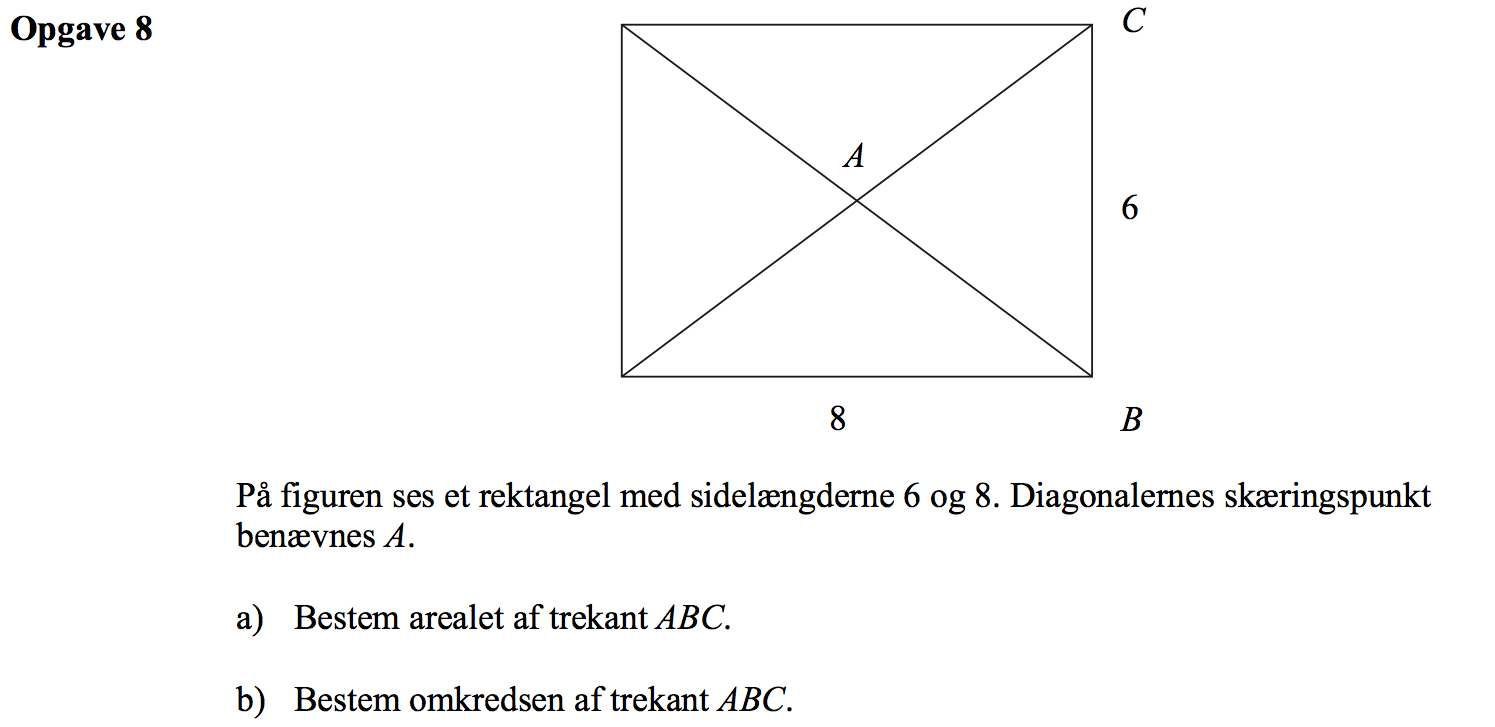
Svar på opgave 8:

1. Højden i trekant ABC er halvdelen af længden af rektanglet, idet diagonalernes skæringspunkt også er midtnormalernes skæringspunkt.

   Dvs. arealet af ΔABC er (1/2)·6·(8/2) = 12

2. AC er halvdelen af hypotenusen i en retvinklet trekant, hvor kateterne er 6 og 8. Dermed kan |AC| findes af Pythagoras læresætning:

   (2·|AC|)² = 6² + 8² ⇔

   4·|AC|² = 36 + 64 ⇔

   |AC|² = 100/4 ⇔

   |AC| = √25 ⇔

   |AC| = 5

   Dermed er omkredsen af ΔABC = 2·5 + 6 = 16

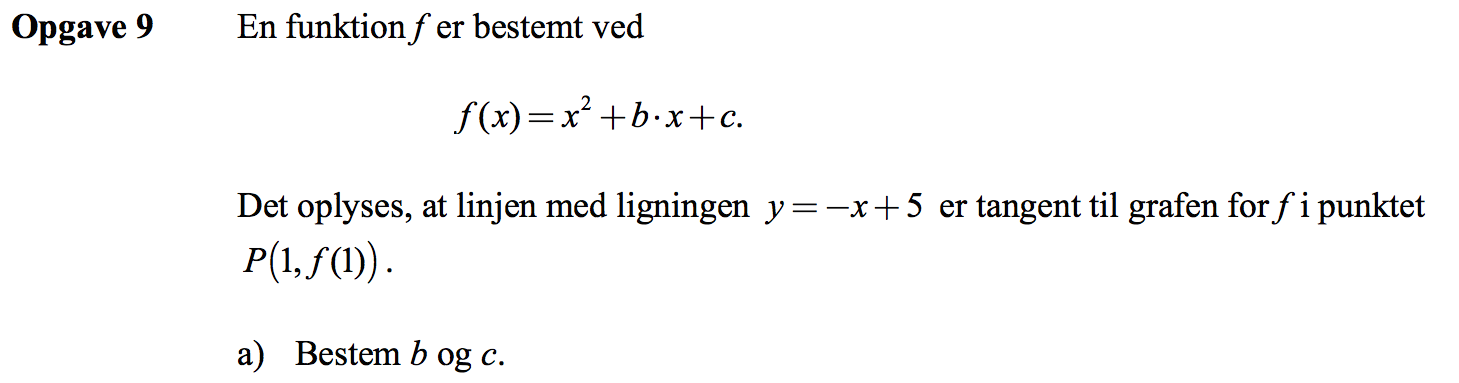
Svar på opgave 9:

1. Til at bestemme b og c har man to ligninger. Den ene er f(1) = y(1) = -1 + 5 = 4. Den anden er f´(1) = -1 (koefficienten til x).

   Man har, at f´(x) = 2x + b. Dette giver:

   1² + b + c = 4 ∧ 2·1 + b = -1 ⇔

   b + c = 4 - 1 ∧ b = -1 - 2 ⇔

   -3 + c = 3 ∧ b = -3 ⇔

   c = 6 ∧ b = -3

   Dvs. b = -3 og c = 6

Svar på opgave 10:

1. Ti-Nspire:

   Man opretter to lister; en for faldhøjde og en for karaterdiameter (diameter).

   faldhøjde:={20,30,50,83,100} ▸ {20,30,50,83,100}

   diameter:={5.,5.6,6.5,7.4,7.8} ▸ {5.,5.6,6.5,7.4,7.8}

   Dernæst laver man en potensregression på de to lister:

   PowerReg faldhøjde,diameter,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   Det ses at a = 0,2758 og b = 2,193

   (Ti-Nspire bruger a og b modsat opgaven.)

2. Man skal finde d(90). Man bruger f1(x), som er oprettet af Ti-Nspire.

   f1(90) ▸ 7.58818

   Dvs. kraterdiameteren er 7,6 cm ved en faldhøjde på 90 cm.

   For at finde den faldhøjde, der svarer til en kraterdiameter på 8,5 cm, skal man løse ligningen d(x) = 8,5. Dette gøres igen ved hjælp af f1(x):

   solve(f1(x)=8.5,x) ▸ x=135.799

   Dvs. faldhøjden, der giver en kraterdiameter på 8,5 cm, er 135,8 cm

3. Man har formlen for procent-procent vækst for en potensfunktion: F_y = (F_x)^a, hvor F_y er fremskrivningsfaktoren for y, F_x er fremskrivningsfaktoren for x og a er eksponenten i potensfunktionen. Her øges x med 50 %, så F_x = 1 + 50 % = 1,5. Eksponenten a er 0,2758. Man beregner vækstraten af y eller d(x) som (F_y - 1)·100 %:

   (1.5^0.2758-1)*100 ▸ 11.832

   Dvs. kraterdiameteren, d(x), vokser med 12 %, når faldhøjden vokser med 50 %.

Svar på opgave 11:

1. Nedenunder er trekanten tegnet i Geogebra.

   

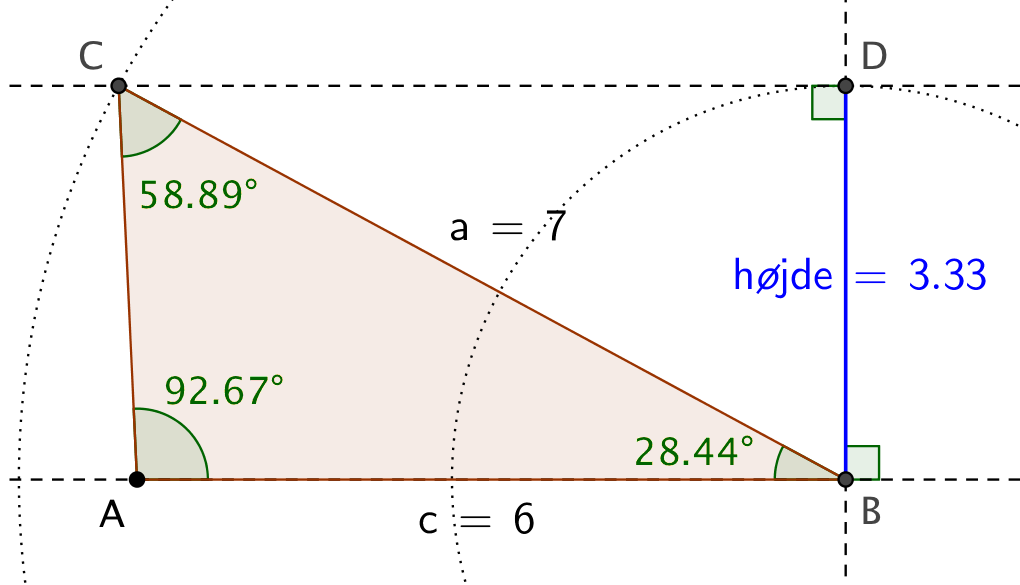
   Siden AB er brugt som grundlinje og højden i C er beregnet ved hjælp af arealformlen for en trekant: areal er lig med en halv grundlinje gange højde.

   Da arealet er 10 og grundlinjen 6, får man højden: 10·2/6 = 10/3.

   Vinkel B kan nu beregnes ved hjælp af den trigonometriske formel: |BC|·sin(∠B) = højde ⇒

   7·sin(∠B) = 10/3 ⇔ sin(∠B) = 10/21 ⇒ ∠B = sin^-1(10/21) ⇔

   ∠B = 28,4369°

   Dvs. vinkel B er 28,4°

   For at finde omkredsen af ΔABC, skal man kende |AC|. Dette gøres ved hjælp af en cosinusrelation:

   cos(28,4369°) = (6² + 7² - |AC|²)/(2·6·7) ⇒

   0,879342 = (85 - |AC|²)/84 ⇔

   85 - 0,879342·84 = |AC|² ⇒

   |AC| = √[11,1353] = 3,33696

   Dvs. omkredsen af ΔABC er 3,33696 + 6 + 7 = 16,3

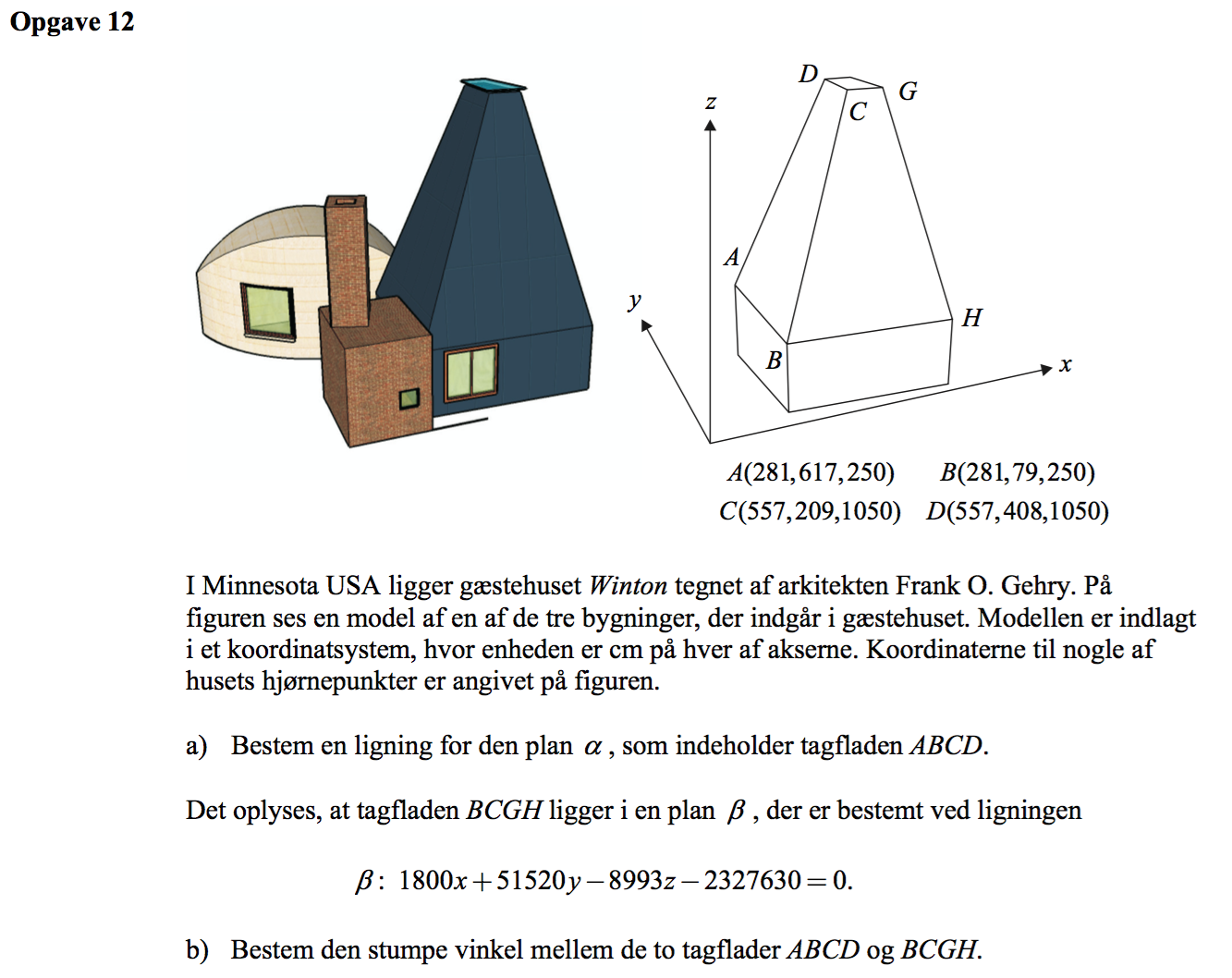
Svar på opgave 12:

1. Man starter med at oprette punkterne A, B og C som vektorer. Herpå opretter man vektorerne AB og AC.

   

   En nomalvektor til planen kaldes n og den sættes lig med krydsproduktet af AB og AC.

   

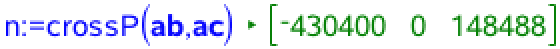
   Man opretter en vektor kaldet AX, der går fra punktet A til et vilkårligt punkt i rummet med koordinaterne (x,y,z).

   

   Når slutpunktet for vektor AX ligger i planen α skal gælde at skalarproduktet af n og AX er lig med nul.

   

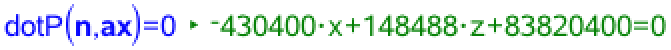
   Dette giver ligningen for α. For at forenkle den faktoriserer man udtrykket på venstre side af lighedstegnet.

   

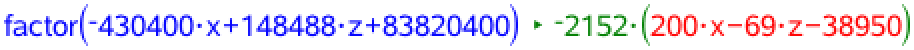
   Ligningen for α er dermed: 200x - 69z - 38950 = 0

2. Vinklen mellem planerne α og β findes ved hjælp af vinklen mellem deres normalvektorer. En normalvektor for planen β kaldes m. Den aflæses af β's ligning ud fra ligningens koefficienter: 1800x + 51520y + -8993z - 2327630 = 0. Det ses at m = (1800,51520,-8993). Denne opretter man i Ti-NSpire:

   

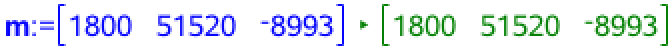
   Man finder nu vinklen mellem vektorerne n og m

   

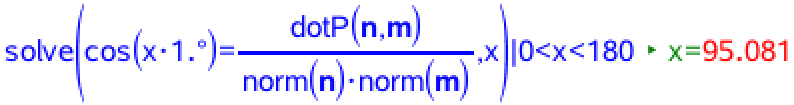
   Da vinklen er større end 90° er dette den stumpe vinkel mellem planerne.

   Dvs. dem stumpe vinkel mellem planerne er 95,1°

   Nedenunder er vinklen fundet i Geogebra som kontrol.

   

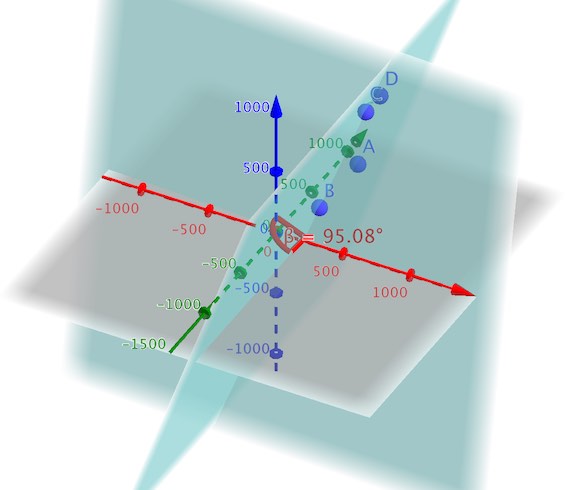
Svar på opgave 13:

1. For punktet (u,v) = (3,4) gælder, at u(t) = 3 og v(t) = 4.

   Man får hastighederne:

   u'(t) = v(t) = 4 og v'(t) = -2u(t) = -2·3 = -6

2. Nedenunder er faseplottet tegnet i Ti-Nspire (x = u og y = v):

   

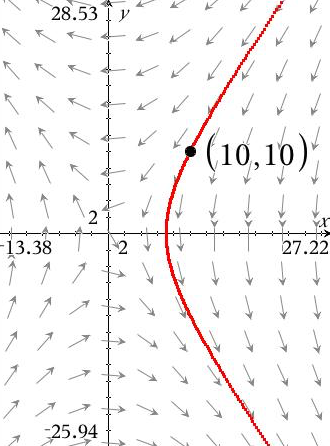
   I punktet A = (u,v) = (10,10) er t = 0. Hvis man går i pilenes retning stiger t, mens den går mod minus uendelig, når man går mod pilenes retning.

Svar på opgave 14:

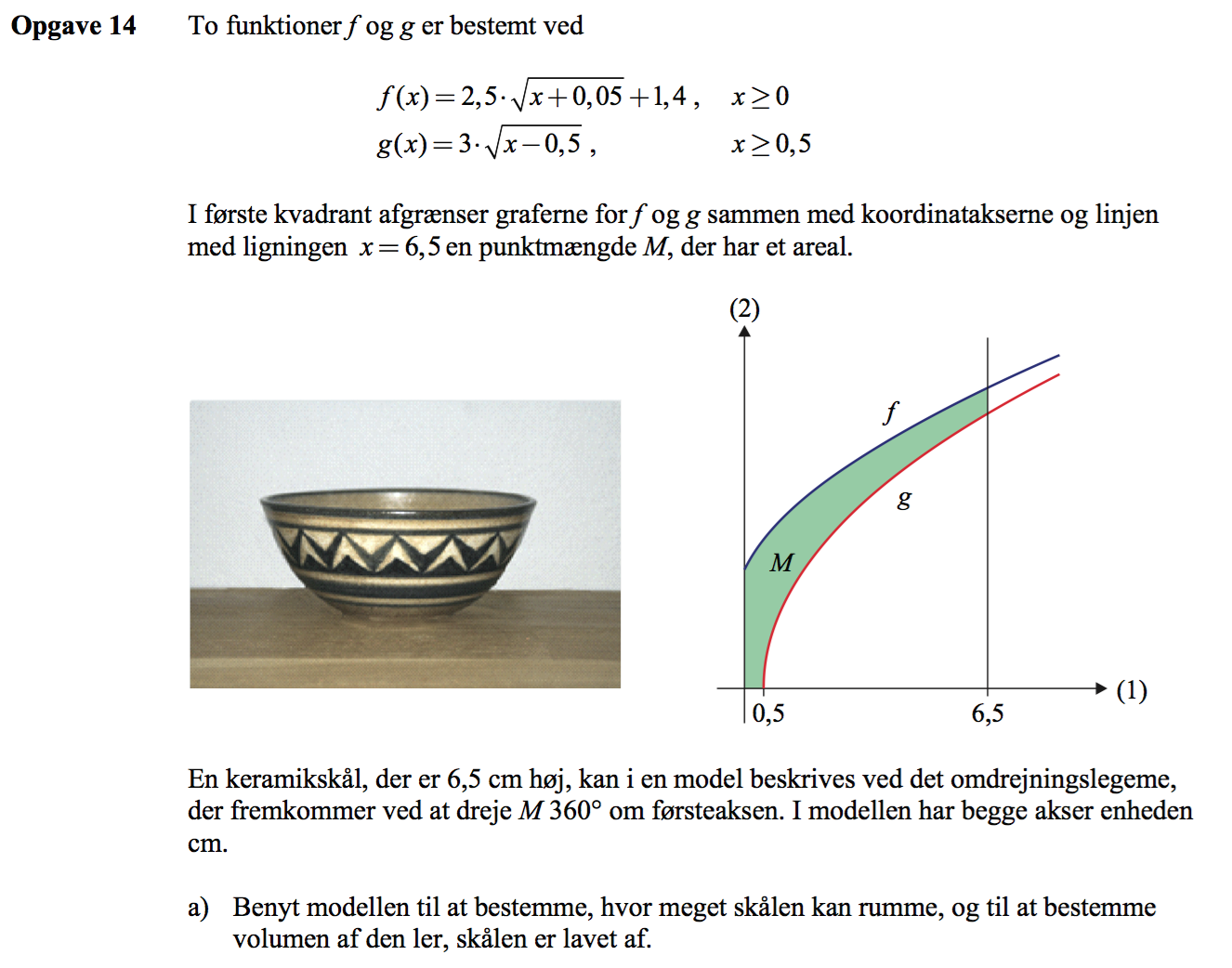
1. Man opretter funktionerne f(x) og g(x).

   

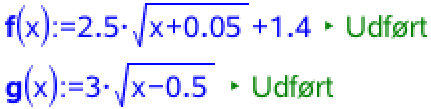
   Det, som skålen kan rumme, er rumfanget af omdrejningslegemet for g(x):

   

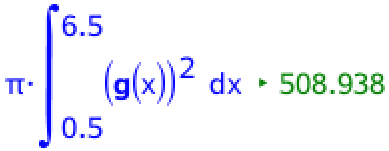
   Dvs. skålen kan rumme 508,9 cm³

   Lerets rumfang er forskellen mellem rumfanget af omdrejningslegemet for f(x) og g(x):

   

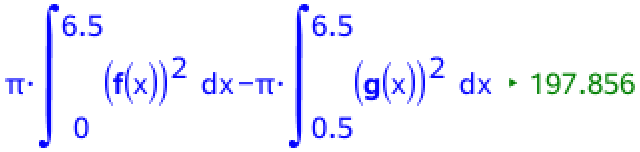
   Dvs. lerets rumfang er 197,9 cm³

Svar på opgave 15:

1. Man har følgende andenordens differentialligning:

   y'' + 0,38y' + 0,55y = 0

   Den har det karakteristiske polynomium P(x) = x² + 0,38x + 0,55.

   Diskriminanten for andengradsligningen x² + 0,38x + 0,55 = 0 er 0,38² - 4·1·0,55 = −2,06.

   Da diskriminanten er negativ, så er f(t) en dæmpet svingning.

2. Man finder forskriften for f(t) med desolve()-kommandoen:

   

   Dvs. f(t) = −15·(0,8270)^t·cos(0,7169·t) - 3,976·(0,8270)^t·sin(0,7169·t)

   Nedenunder er grafen for f(t) vist for de første 10 sekunder.

   

Svar på opgave 16:

1. Arealet af en trekant er en halv gange højde gange grundlinje. Her er grundlinjen lig med x og højden er lig med f(x). Man får derfor følgende areal af ΔOPQ: (1/2)·x·f(x) = (1/2)·x·(1 - x²) = (1/2)·(x - x²)

   ΔOPQ er retvinklet og kateterne er x henholdsvis f(x). Hypotenusen er derfor √[x² + (1 - x²)²].

   Omkredsen er: |OQ| + |QP| + |PO| = x + (1 - x²) + √[x² + (1 - x²)²] = √[x⁴ - x² + 1] - x² + x + 1

2. Man opretter T(x) og d(x) som funktioner i Ti-Nspire:

   

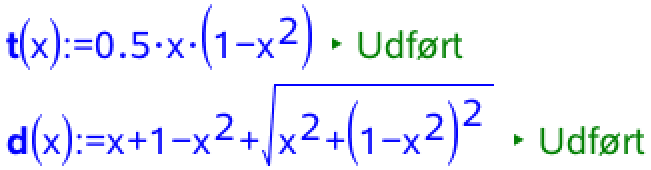
   Dernæst bruger man fMax()-kommandoen til at finde de x-værdier, der giver maksimumsværdien for henholdsvis areal og omkreds:

   

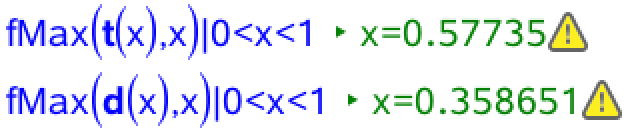
   Det ses dermed, at det ikke er samme x-værdi, der giver maksimum for både areal og omkreds.