Svar på opgave 1:

1. Vektoren (2,1) er retningsvektor for l og dermed er dens tværvektor (-1,2) retningsvektor for m.

   Man får parameterfremstillingen for m: (x,y) = (3,4) + s·(-1,2), s ∈ R

Svar på opgave 2:

1. Man har h(x) = g(x)/f(x) = 3^x/2^x = (3/2)^x

   Fremskrivningsfaktoren er grundtallet i potensen, dvs. 3/2 eller 1,5

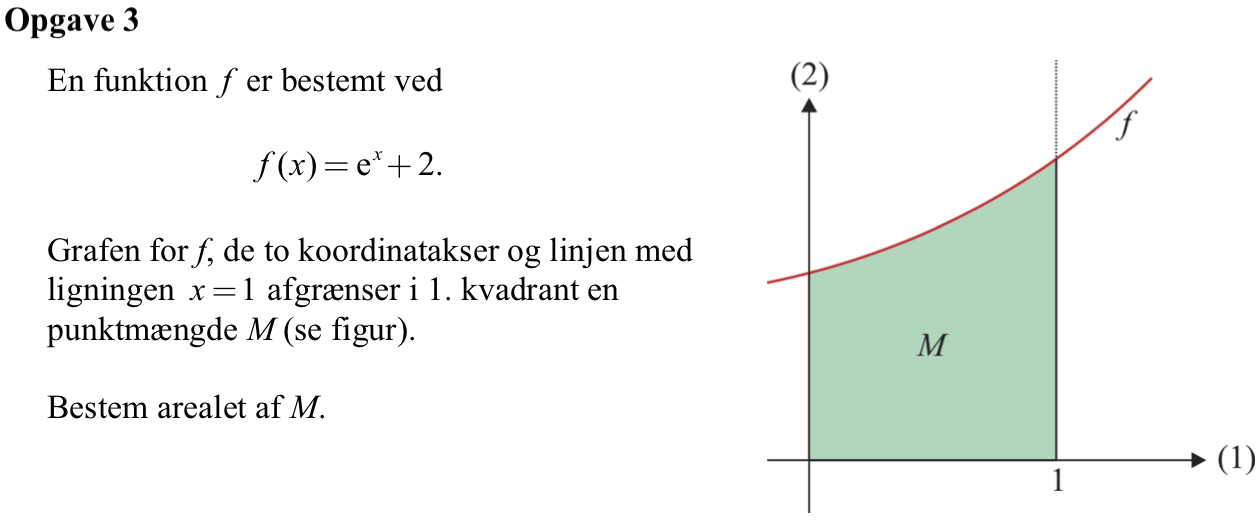
Svar på opgave 3:

1. Arealet af M er integralet af f(x)·dx fra x = 0 til x = 1.

   Dette er: [e^x + 2x]₀¹ = e + 2 - 1 = e + 1 = 3,718

Svar på opgave 4:

1. V = (4/3)·π·r³ ⇒ r = ³√[3·V/(4·π)].

   Man indsætter V = (32/3)·π og får: r = ³√[3·(32/3)·π/(4·π)] = ³√8 = 2

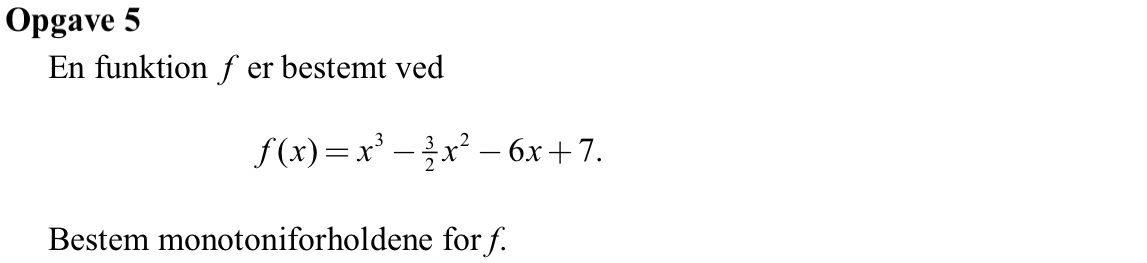
Svar på opgave 5:

1. Man skal finde fortegn for f´(x). Man får at f´(x) = 3x² - 3x - 6.

   Nulpunkterne for f´(x) er løsningerne til andengradsligningen: 3x² - 3x - 6 = 0 ⇔

   x = (3 ± √[9 + 4·3·6])/6 ⇔

   x = (3 ± √81)/6 ⇔

   x = (3 ± 9)/6 ⇔

   x = -1 ∨ x = 2

   f´(x) er en parabel der vender grenene opad, derfor er f´(x) mindre end 0 for -1 < x < 2 og større end 0 ellers. Man får monotoniforholdene:

   f(x) er voksende for x < -1

   f(x) er aftagende for -1 < x < 2

   f(x) er voksende for 2 < x

Svar på opgave 6:

1. Tangentens ligning kan skrives: y = a·x + b. Her er a lig med hældningen, som findes af differentialligningen ved at indsætte y = 4. Man får: a = 3·4 + 5 = 17.

   Konstanten b findes ved at indsætte punktet (x,y) = (1,4) i ligningen: y = 17x + b, hvilket giver: 4 = 17·1 + b ⇒ b = 4 -17 = -13.

   Tangentens ligning er dermed: y = 17x - 13

Svar på opgave 7:

1. Man opretter to lister med data for henholdsvis år og antal reklametimer:

   aar:={2000,2005,2008,2009,2010}-2000 ▸ {0,5,8,9,10}

   reklametimer:={4963,8249,10296,12459,13661} ▸ {4963,8249,10296,12459,13661}

   Man bruger kommandoen for eksponential regression på de to lister (kommandoen findes under menuen: statistik ▸ statistiske beregninger ▸ eksponentiel regression...):

   ExpReg aar,reklametimer,1: CopyVar stat.RegEqn,f1: stat.results ▸

   [["Titel","Eksponentiel regression"]
   ["RegEqn","a*b^x"]
   ["a",4946.4469957229]
   ["b",1.1047392417559]
   ["r²",0.99172918866747]
   ["r",0.99585600799888]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Her aflæses a til 1,1047 og b til 4946,4

   Bemærk at Ti-Nspire bruger a og b i modsat betydning af opgaven.

2. Fordoblingskonstanten er ln(2)/ln(1,10474) = 6,959

3. f´(6) findes med kommandoen

   derivative(4946.45*(1.10474)^t,t)|t=6 ▸ 895.69

   Dvs. f´(6) = 895,7 reklametimer/år

   Dette tal er ændringen i antal reklametimer pr. år efter 6 år.

Svar på opgave 8:

1. Man opretter vektorerne:

   a:=[−3,7] ▸ [−3,7]

   b:=[1,−4] ▸ [1,−4]

   Man finder vinklen mellem dem med kommandoen:

   solve(cos(x*1.°)=dotP(a,b)/(norm(a)*norm(b)),x)|0<x<180 ▸ x=170.838

   Dvs. vinklen er 170,1°

2. Arealet er 0,5 gange den numeriske værdi af determinanten til a og b.

   Det giver areal: 0,5·|det([-3,7],[1,-4])| = 0,5·|12-7| = 2,5

Svar på opgave 9:

1. Man finder mængden af affald ved at definerer w(t) og indsætte t = 0:

   w(t):=519.9/(1+0.098*exp(−0.434*t)) ▸ Udført

   w(0) ▸ 473.497

   Dvs. affaldsmængden er 473,4 kilo pr. indbygger

2. Grafen for w(t) er tegnet i Geogebra og vist nedenunder.

   

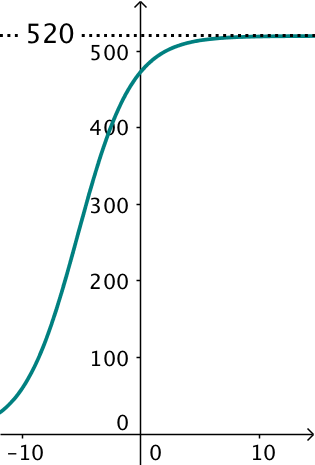
   Af grafen ses, at affaldsproduktionen nærmer sig 520 kilogram pr. indbygger om året for tiden gående mod uendelig, dvs. påstanden er rigtig.

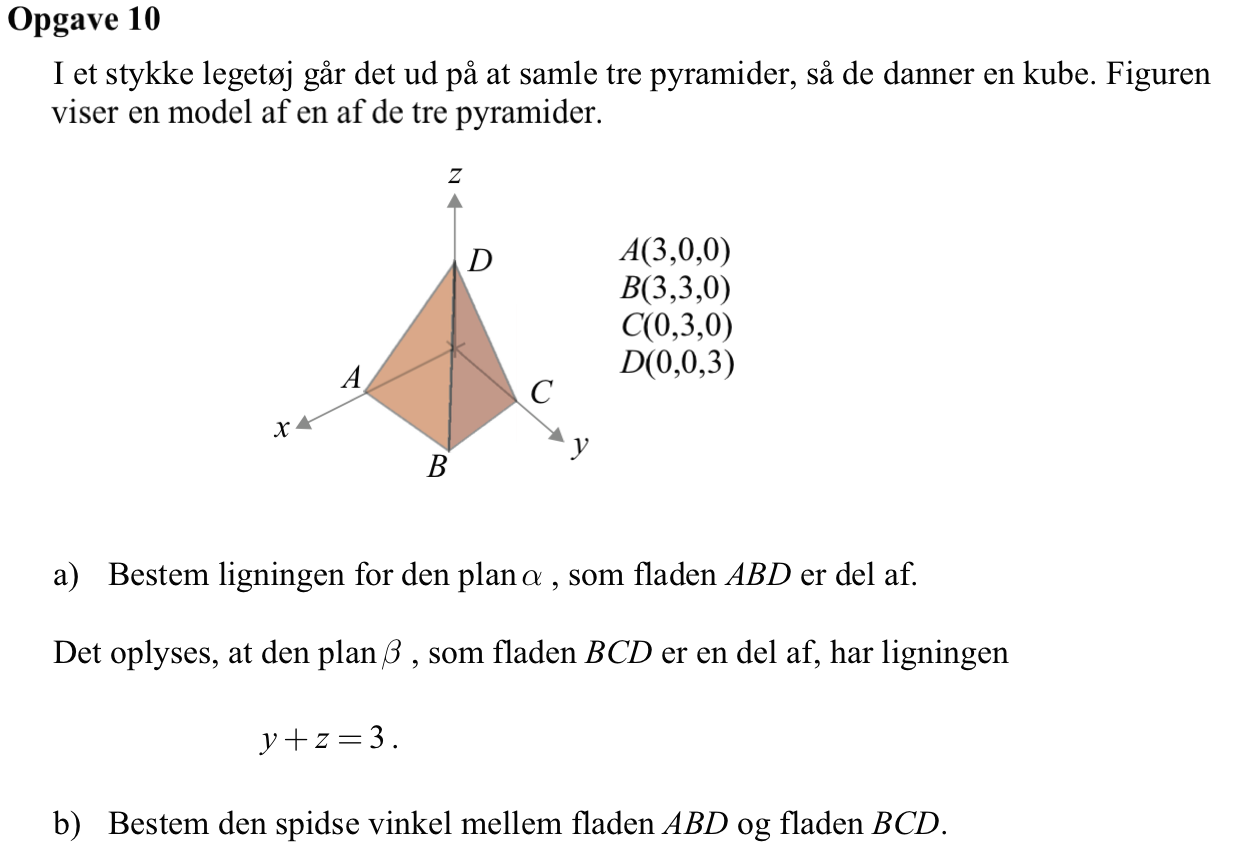
Svar på opgave 10:

1. Punkterne oprettes som stedvektorer:

   a:=[3,0,0] ▸ [3,0,0]

   b:=[3,3,0] ▸ [3,3,0]

   c:=[0,3,0] ▸ [0,3,0]

   d:=[0,0,3] ▸ [0,0,3]

   Vektorerne ab og ad oprettes:

   ab:=b-a ▸ [0,3,0]

   ad:=d-a ▸ [−3,0,3]

   abxad:=crossP(ab,ad) ▸ [9,0,9]

   Planen α's normalvektor oprettes som denne vektor divideret med største fælles divisor for at få små hele tal:

   n:=[9,0,9]/9 ▸ [1,0,1]

   Planens ligning findes med kommandoen:

   dotP(n,[x,y,z]-a)=0 ▸ x+z-3=0

   Her benytter man, at skalarproduktet mellem normalvektoren og en vilkårlig vektor i planen er 0.

   Ligningen for planen α er x + z - 3 = 0

2. Normalvektoren til β aflæses af β's ligning til m = (0,1,1). Den spidse vinkel mellem planerne findes som den spidse vinkel mellem deres normalvektorer:

   solve(cos(x*1.°)=abs(dotP(n,m))/(norm(n)*norm(m)),x)|0<x<180 ▸ x=60.

   Dvs. at den spidse vinkel mellem fladerne ABD og BCD er 60°

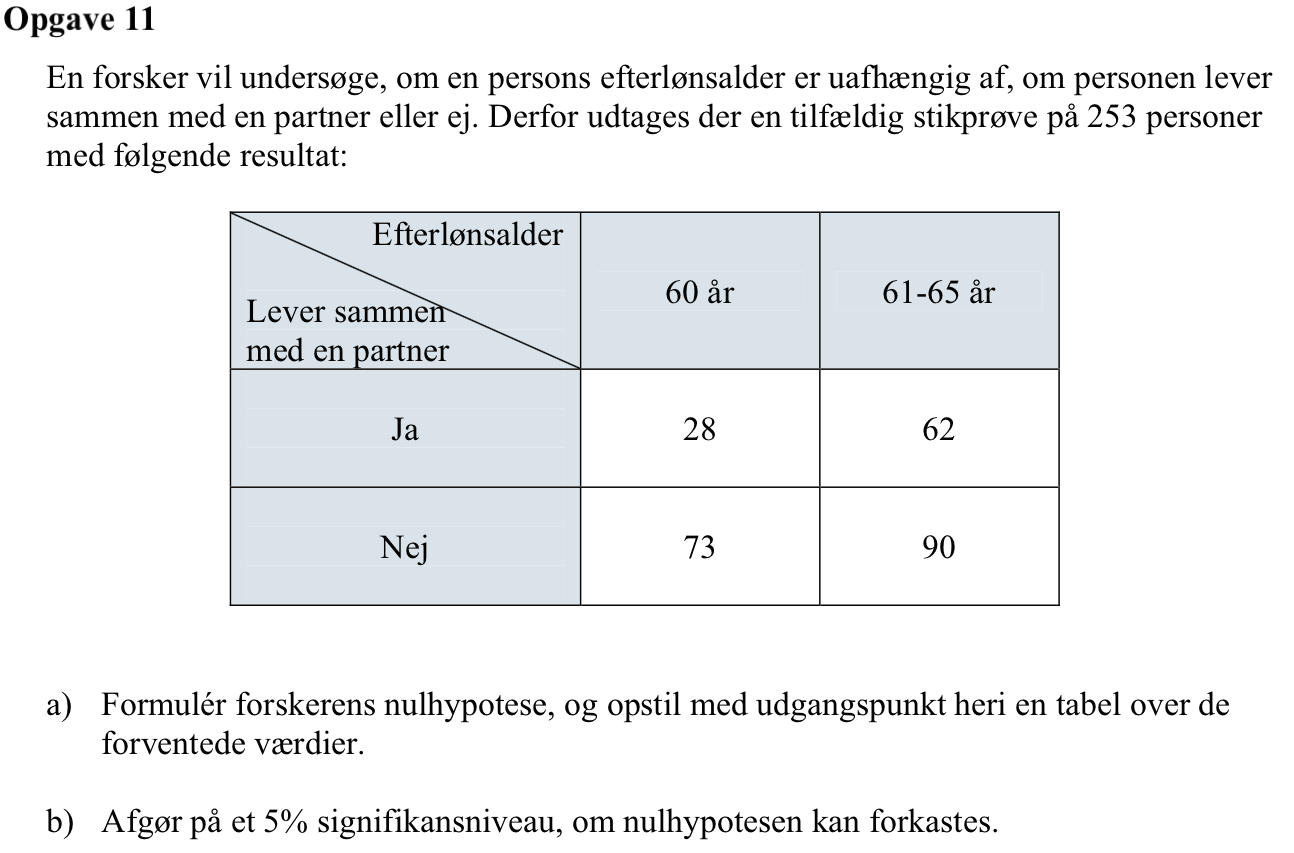
Svar på opgave 11:

1. Nulhypotesen er, at efterlønsalder er afhængig af om, man har en partner

   Man definerer en matrice med data:

   

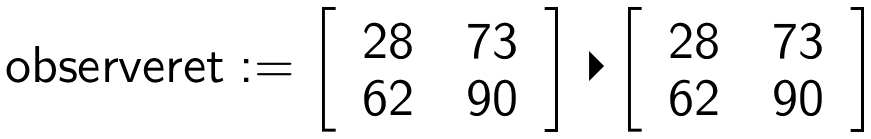
   Man laver en chi-i-anden uafhængighedsanalyse på data:

   χ²2way observeret: stat.results ▸

   [["Titel","χ²-uafhængighedstest"]
   ["χ²",4.5205086330396]
   ["PVal",0.033490873150682]
   ["df",1.]
   ["ExpMatrix","[...]"]
   ["CompMatrix","[...]"]]
   

   Herfra findes de forventede værdier med kommandoen:

   χ²2way observeret: stat.ExpMatrix ▸

   

2. Af resultatlisten i a) ses at PVal = 0,033 = 3,3 %. Da dette er mindre end 5 % forkastes nulhypotesen.

Svar på opgave 12:

1. Man opretter f(x):

   f(x):=a*x²+b*x+c

   Man bruger solve-kommandoen til at finde a, b og c:

   solve(f(0)=220 and f(1280./2)=80 and f(1280)=220,a,b,c) ▸ a=0.0003418 and b=−0.4375 and c=220.

   Disse værdier indsættes og man får forskriften: f(x) = 0,000342x² - 0,4375x + 220

   Denne forskrift oprettes :

   f(x):=0.000342*x²-0.4375*x+220 ▸ Udført

   Længden beregnes, idet x₁ = 0 og x₂ = 1280:

   integral(sqrt(1+(derivative(f(x),x))²),x,0,1280) ▸ 1319.78

   Længden af bærekablet er 1319,8 m

Svar på opgave 13:

1. Man skal finde c(t)', når c(t) = 1,5 μg/L: −0,035·1,5 μg/L/time = −0,0525 μg/L/time

2. Man bruger desolve() kommandoen:

   deSolve(c'=−0.035*c and c(0)=2.,t,c) ▸ c=2.*0.965605^t

   Dvs. løsningen er c(t) = 2·0.9656^t

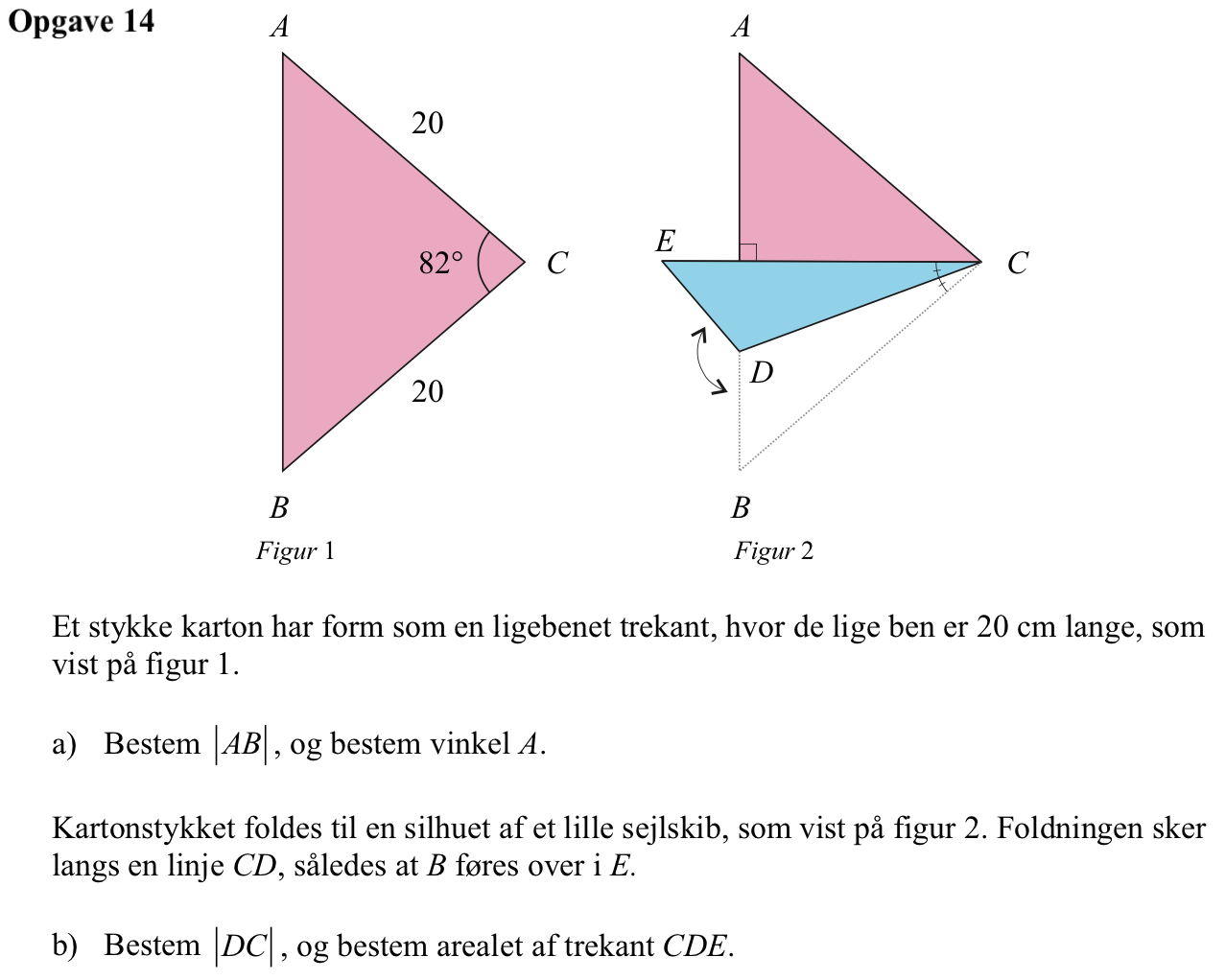
Svar på opgave 14:

1. Topvinklen i den ligebenede trekant er 82°.

   ∠A er grundvinklen i trekanten. ∠A = (180° - 82°)/2 = 49°

   |AB| er grundlinjen i trekanten. |AB| = 2·20·sin(82°/2) = 26,24

2. Det bemærkes, at trekant BCD og trekant CDE er kongruente. Dette fremgår af, at de to trekanter forestiller det sammen stykke papir før og efter foldningen.

   Dette gør, at ∠BCD = ∠DCE = 82°/4 = 20,5°.

   Man bruger en sinusrelation: |DC|/sin(∠B) = |CE|/sin(∠CDE). Her er:

       ∠B = (180° - 82°)/2 = 49°.

       ∠CDE = 180° - 49° - 20,5° = 110,5°.

       |CE| = 20.

   Dette indsættes i sinusrelationen og man får, idet |DC| kaldes x:

   solve(x/sin(49*1.°))=20/sin(106.5*1.°),x) ▸ x=16.1147

   Dvs. |DC| = 16,11

   Arealet er 0,5·[højde]·grundlinje =

       0,5·[|DC|·sin(∠DCE)]·20 = 0.5·[16,1147·sin(20,5°)]·20 = 56,43

Svar på opgave 15:

1. Graferne tegnes i Geogebra, mellemrummet M af træ markeres med brun:

   

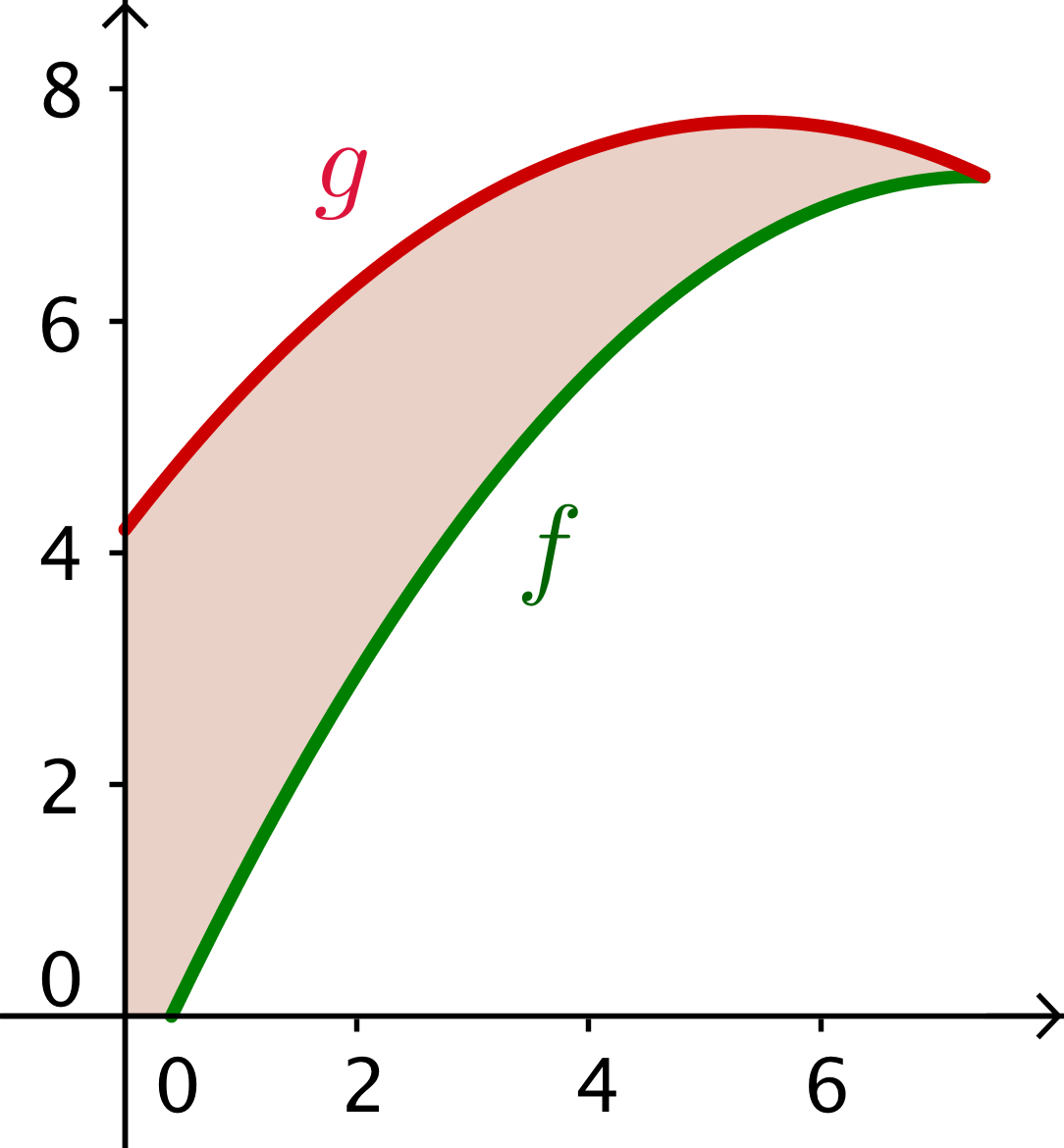
   Højden af skålen er x-værdien af det første skæringspunkt mellem f og g i første kvadrant:

   f(x):=−0.15*x²+2.205*x-0.858 ▸ Udført

   g(x):=−0.12*x²+1.3*x+4.2 ▸ Udført

   solve(f(x)=g(x),x) ▸ x=7.4082 or x=22.758

   Dvs. højden er 7,408 cm

2. Rumfanget beregnes ved formlen for omdrejningslegemer.

   Man finder først f's skæring med x-aksen:

   solve(f(x)=0,x) ▸ x=0.4 or x=14.3

   Dvs. [f(x)]² skal integreres fra x = 0,4 til x = 7,408, mens [g(x)]² integreres fra 0 til 7,408. Man får:

   π*integral((g(x))²,x,0,7.40825)-π*integral((f(x))²,x,0.4,7.40825) ▸ 485.22

   Dvs. rumfanget af træet er 485,22 cm³