Svar på opgave 1:

1. Mangler

Svar på opgave 2:

1. Mangler

Svar på opgave 3:

1. Mangler

Svar på opgave 4:

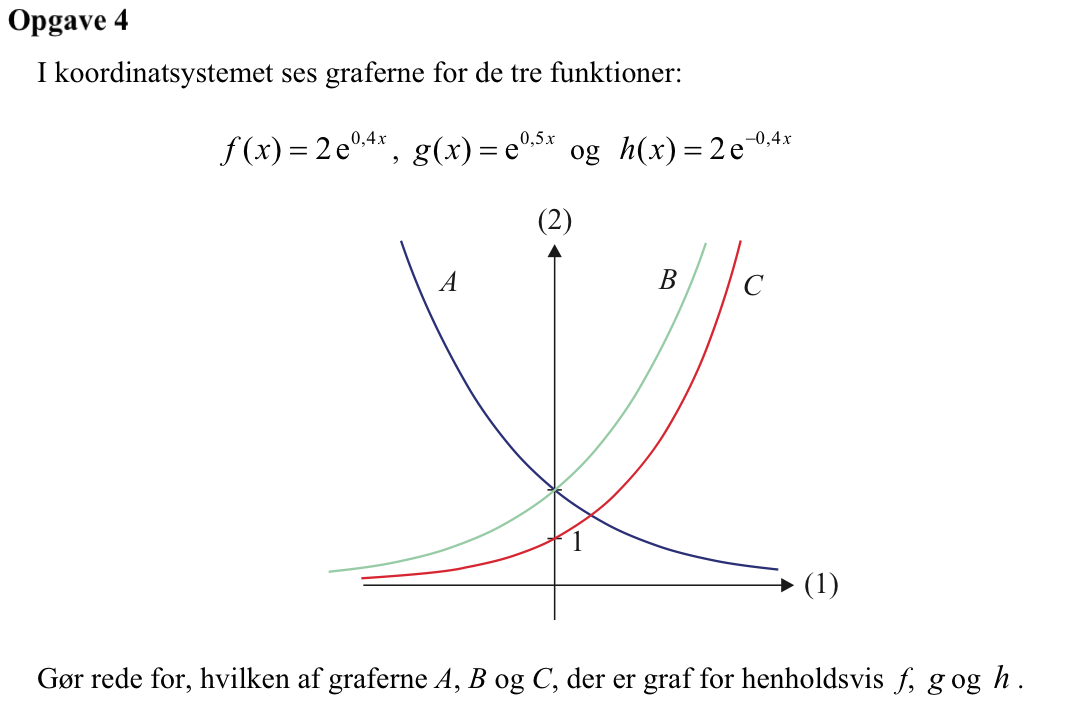
1. De tre funktioner er af formen b·a^x (eksponentialfunktioner). For disse gælder, at b = skæring med y-aksen, a>0 viser, at funktionen er voksende, mens a<0 viser, at funktionen er aftagende.

   Heraf ses at f(x) (b=2 og a<0) svarer til kurve B, g(x) (b=1 og a<0) svarer til kurve C og h(x) (b=2 og a<0) svarer til A.

Svar på opgave 5:

1. l har retningsvektoren (8,3). Det betyder at m's retningsvektor er tværvektoren til retningsvektoren for l.

   Tværvektoren til (8,3) er (-3,8) og da m skal gå igennem punktet (8,10), får man dens parameterfremstilling til:

   m: (8,10) + s·(-3,8), s∈R

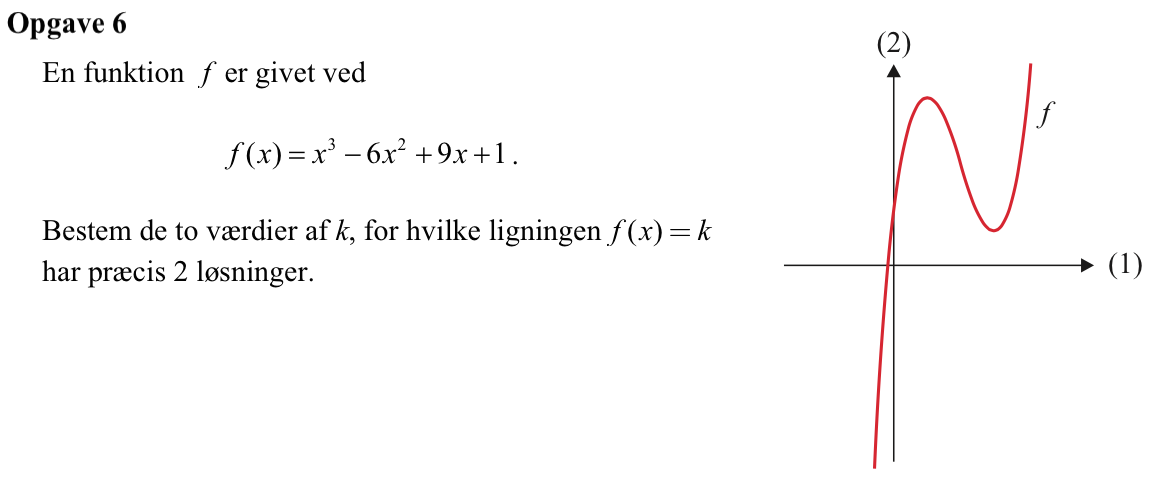
Svar på opgave 6:

1. De værdier af k, hvor ligningen f(x) = k har netop 2 løsninger, er y-værdierne for de lokale ekstrema til f(x). Dette er vist på nedenstående figur:

   

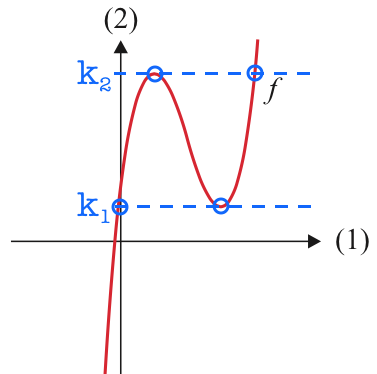
   Man differentierer f(x) og sætter den afledte funktion lig med 0 for at finde ekstremums­punkterne.

   f´(x) = 0 ⇒ 3x² - 12x + 9 = 0 ⇒ x = 1 ∨ x = 3. Disse x-værdier indsættes i f(x) for at finde y-værdierne af ekstremums­punkterne: f(1) = 5 og f(3) = 1.

   Dette vil sige, at værdier af k, der giver netop 2 løsninger af ligningen f(x) = k er: k = 1 og k = 5

Svar på opgave 7:

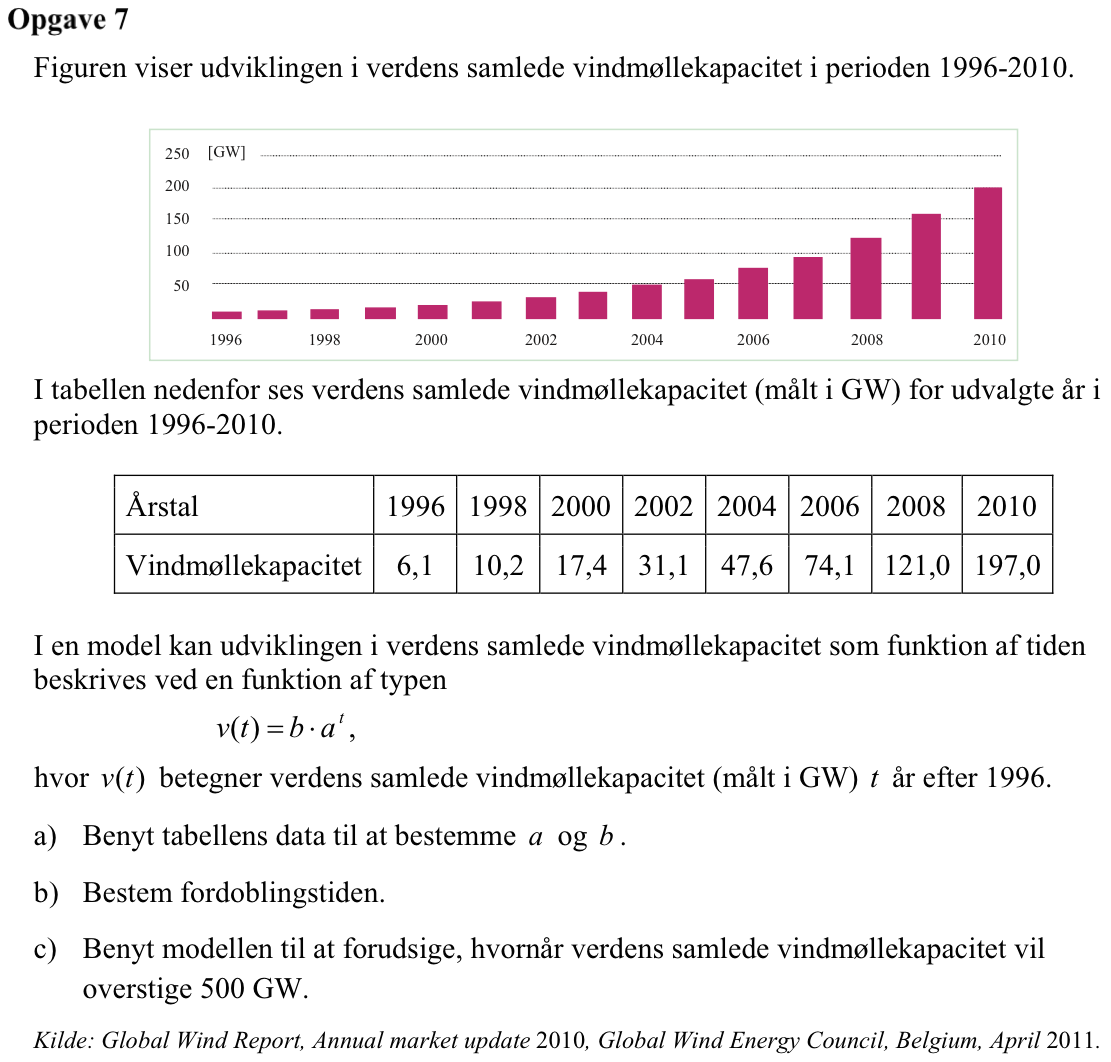
1. Antal år efter 1996 og udvinklingen i vindmølle­kapacitet oprettes som lister:

   antal_år:={1996,1998,2000,2002,2004,2006,2008,2010}-1996 ▸ {0,2,4,6,8,10,12,14}

   kapacitet:={6.1,10.2,17.4,31.1,47.6,74.1,121.,197.} ▸ {6.1,10.2,17.4,31.1,47.6,74.1,121.,197.}

   Man laver eksponentiel regression på de to lister:

   ExpReg antal_år,kapacitet,1: CopyVar stat.RegEqn,f1: stat.results ▸

   

   Det bemærkes, at Ti-Nspire bruger a og b modsat opgaven. Man får derfor:

   a = 1,2799 og b = 6,3999

2. Fordoblingstiden er ln(2)/ln(a) år = ln(2)/ln(1,2799) år = 2,80 år

3. Man bruger f1(x), som man fandt ved regressionsanalysen. Man skal løse f1(x) = 500 med hensyn til x og lægge dette tal til 1996 og runde op. Man får:

   solve(f1(x)=500,x) ▸ x=17.659

   Dvs. at verdens vindmøllekapacitet vil overstige 500 GW i 1996 + 18 = 2014

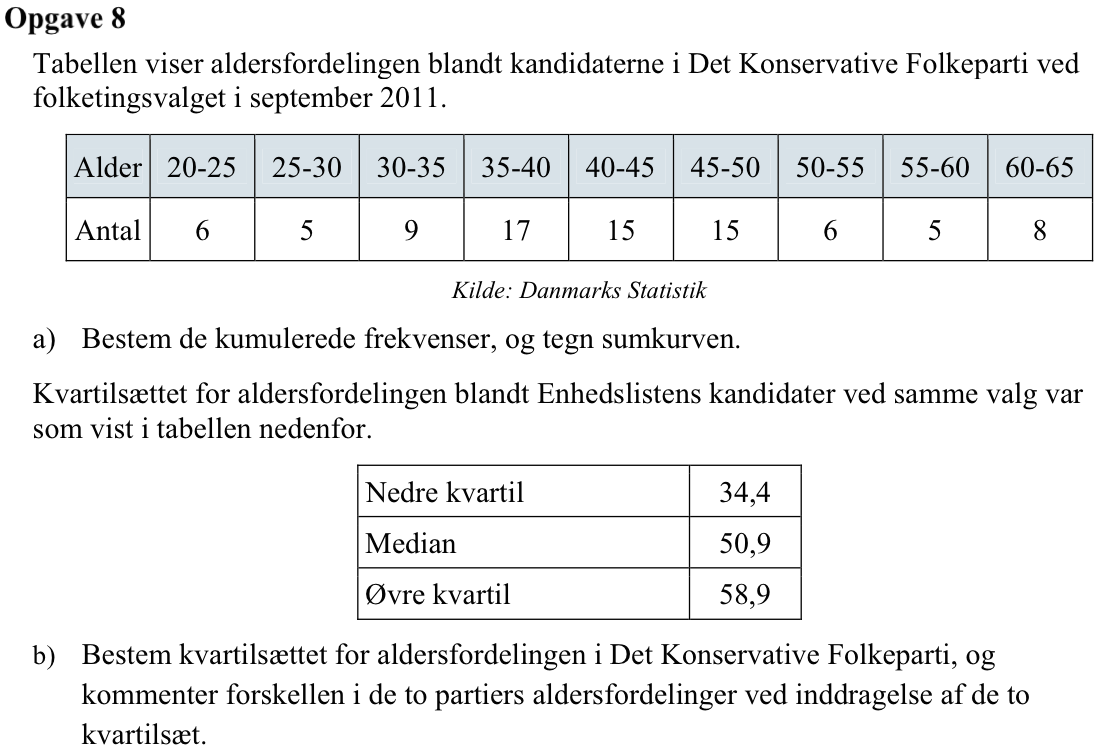
Svar på opgave 8:

1. Man opretter lister for alder, antal personer i hvert aldersinterval og den kummulerede frekvens for personer i hvert interval.

   alder:={25,30,35,40,45,50,55,60,65} ▸ {25,30,35,40,45,50,55,60,65}

   antal:={6,5,9,17,15,15,6,5,8} ▸ {6,5,9,17,15,15,6,5,8}

   kumm_frekvens:=cumulativeSum(antal/sum(antal))*1. ▸ {0.06977,0.12791,0.23256,0.43023,0.60465,0.77907,0.84884,0.90698,1.}

   Ved hjælp af alders-listen og listen over kummulerede frekvenser tegnes en sumkurve som vist nedenunder.

   

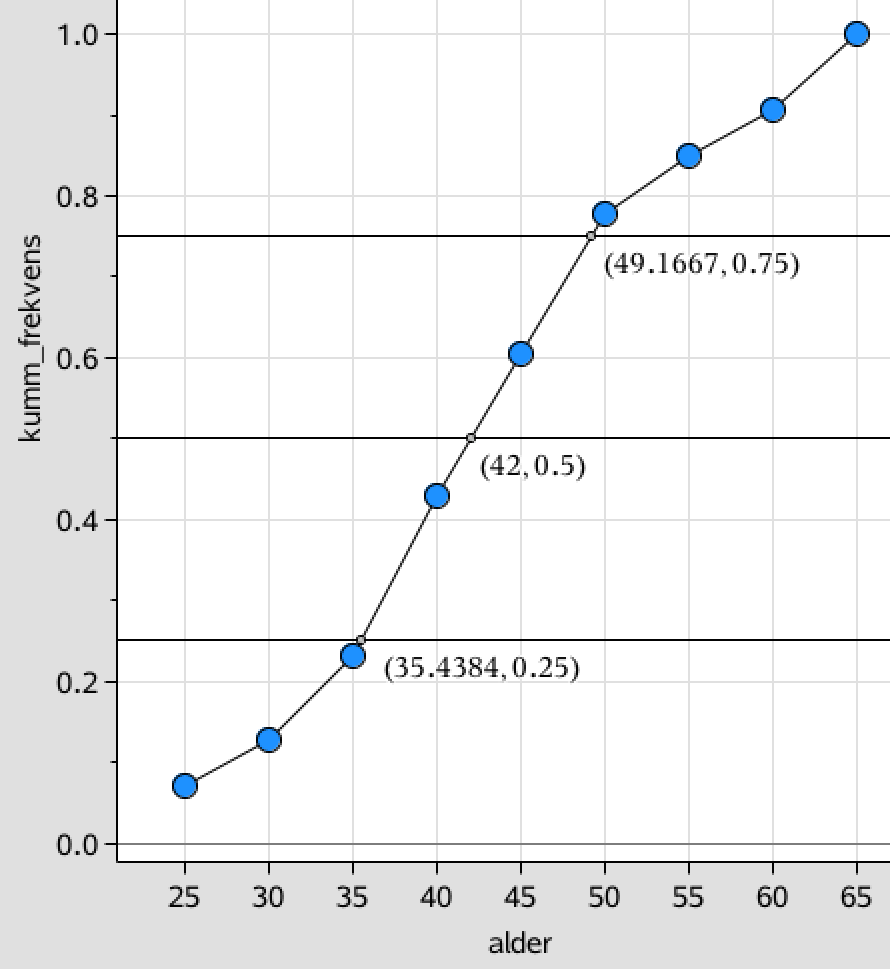
   Figuren indeholder også sumkurvens skæringspunkter med linjerne for de kummulerede frekvenser 0,25; 0,50 og 0,75, der skal bruges til kvartilsættet.

2. Af skæringspunkterne på ovenstående figur fremgår det, at kvartilsættet for alderen de konservative folketingskandidater er 1. kvartil = 35,4 år, median = 42,0 år og tredje kvartil = 49,2 år.

Svar på opgave 9:

1. Man opretter B(x):

   b(x):=0.69*x^1.48 ▸ Udført

   Bladarealet for et 10 cm langt blad er

   b(10) ▸ 20.838

   Dvs. arealet er 20,8 cm²

2. Man finder den procentvise forøgelse af bladets areal ved hjælp af procent-procent formlen, der gælder for potensfunktioner:

   (1.25^1.48-1)*100 ▸ 39.132

   Dvs. bladarealet øges med 39 %, når bladlængden øges med 25 %.

3. Man opretter O(x):

   o(x):=3*x-8 ▸ Udført

   Man finder skæringspunkter mellem de to kurver for bladlængder mellem 3 cm og 17 cm:

   solve(b(x)=o(x),x)|3≤x≤17 ▸ x=5.652 or x=13.52

   Dvs. de bladlængder hvor de to modeller giver samme areal er længderne 5,65 cm og 13,5 cm

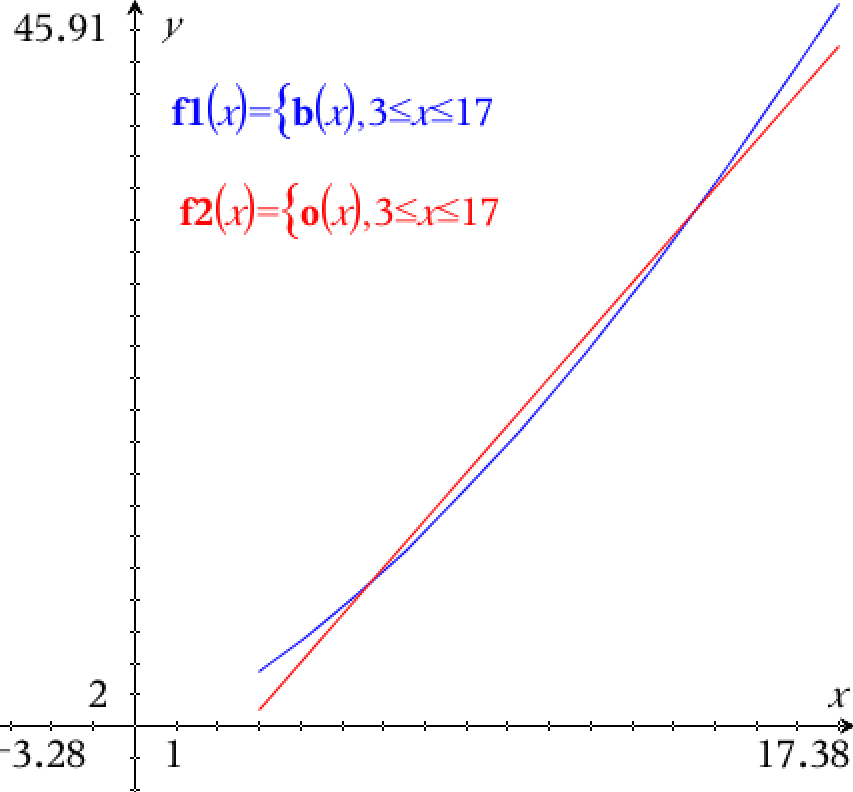
   De to funktioner B(x) og O(x) er afbildet nedenunder.

   

Svar på opgave 10:

1. Man opretter f(x):

   f(x):=3*x⁴-8*x³-30*x²+72*x+27 ▸ Udført

   Man finder f´(x):

   derivative(f(x),x) ▸ 12*x³-24*x²-60*x+72

   Dvs. f´(x) = 12x³ - 24x² - 60x + 72

   Man skal bestemmer de x for hvilke f´(x) = 0 og lave en fortegnsbestemmelse for f´(x) omkring disse x-værdier for at finde ud af f´(x) skifter fortegn omkring nulpunktet. Hvis den gør, er der tale om ekstremum, hvis ikke er der tale om en vandret vendetangent og dermed ikke ekstremum.

   Man finder nulpunkterne for f´(x):

   solve(derivative(f(x),x)=0,x) ▸ x=−2 or x=1 or x=3

   Fortegnsundersøgelse:

   derivative(f(x),x)|x=−3 ▸ −288

   derivative(f(x),x)|x=0 ▸ 72

   derivative(f(x),x)|x=2 ▸ −48

   derivative(f(x),x)|x=4 ▸ 216

   Det ses at f´(x) skifter fortegn omkring alle nulpunkter, som dermed alle er ekstremums­punkter.

   Dvs. f(x) har ekstremumspunkter for x=−2, x=1 eller x=3

Svar på opgave 11:

1. Man bruger en sinusrelation til at finde vinkel B:

   solve(sin(vb*1.°)/8=sin(40.°)/6,vb)|0<vb<90 ▸ vb=58.987

   Dvs. vinkel B er 59,0°

2. Nedenstående tegning viser trekant ABC med trekant ABD. Punktet E er fodpunktet for højden (h) fra D til siden AB.

   

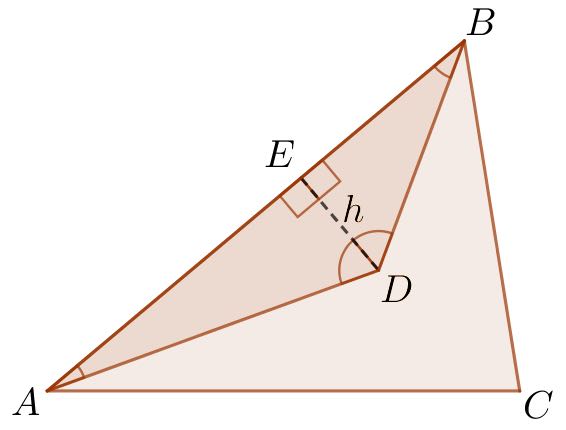
   Arealet af ΔABD er 0,5·|AB|·h.

   Man finder først |AB| ved hjælp af en sinusrelation:

   solve(sin(180°-(40°+58.987°))/ab=sin(40.°)/6,ab) ▸ ab=9.21975

   Højden findes dernæst ved en trigonometriske formel h = |AD|·sin(∠DAB).

   Her ved man, at ∠DAB er halvdelen af ∠A, dvs. 20°.

   |AD| kan igen findes ved hjælp af en sinusrelation, idet man ved, at AD er den modstående side til ∠DAB:

   |AD|/sin(29,493°) = 9,21975/sin(130,507°) ⇒|AD| = 9,21975·sin(29,493°)/sin(130,507°) ⇒ |AD| = 5,9699

   Højden er dermed |AD|·sin(∠DAB) = 5,9699·sin(20°) = 2,0418

   Dvs. areal af ΔABD = 0,5·højde·grundlinje = 0,5·h·|AB| = 0,5·2,0418·9,2198 = 9,41

   Idet man kender |AB| samt AB's hosliggende vinkler ∠DAB = 20° og ∠ABD = 58,987°/2 = 29,493°, kan man også bruge formlen:

   Areal(ΔABD) = 0,5·|AB|²·(1/tan(∠DAB)+1/tan(∠ABD)) = 9,413.

   Udledning af formel. Man betragter følgende trekant ABC, hvor α og β er mindre end 90°:

   

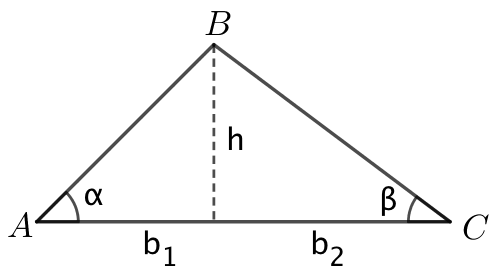
   Areal af ΔABC = 0,5·h·|AC| = 0,5·h·(b₁ + b₂) = 0,5·h·[h/tan(α) + h/tan(β)] = 0,5·h²·[1/tan(α) + 1/tan(β)].

Svar på opgave 12:

1. Man opretter punkterne A, B, C og E som stedvektorer (D viser sig at kunne udelades).

   a:=[3,0,0] ▸ [3,0,0]

   b:=[4,3.5,1] ▸ [4,3.5,1]

   c:=[1,3.5,4] ▸ [1,3.5,4]

   e:=[0,3,0] ▸ [0,3,0]

   Man finder krydsproduktet AB×AC som er en normalvektor til planen:

   crossP(b-a,c-a) ▸ [10.5,−6,10.5]

   Denne vektor divideres med 1,5 for at få små hele tal, og man får normalvektoren n:

   n:=[10.5,−6,10.5]/1.5 ▸ [7.,−4.,7.]

   For at et punkt P = (x,y,z) skal ligge i planen, må der gælde, at AP·n = 0 eller (OP-OA)·n = 0. Denne betingelse omskrives til en ligning i x, y og z:

   dotP(n,[x,y,z]-a)=0 ▸ 7.*x-4.*y+7.*z-21.=0

   Dvs. planens ligning er 7x - 4y + 7z = 21

2. Planen α's normalvektor n = (7,−4,7) er en retningsvektor for l, da l er vinkelret på α. Da l desuden går i gennem punktet E = (0,3,0) har den parameterfremstillingen:

   [x,y,z]=e+t*n ▸ [x=7*t,y=3-4*t,z=7*t]

   Dvs. linjens parameterfremstilling kan skrives (x,y,z) = (7t,3-4t,7t) eller l: (x,y,z) = (0,3,0) + t·(7,-4,7), t∈R

   Man har fire ligninger til at bestemme værdierne for x, y, z og t for skæringspunktet. Værdien af t er man ikke bedt om, men den indgår i beregningen. Disse fire ligninger er 1) planens ligning, 2) linjens parameterfremstillingen for x, 3) linjens parameterfremstillingen for y og 4) linjens parameterfremstillingen for z. Man får:

   solve(7.*x-4*y+7*z-21=0 and x=7*t and y=3-4*t and z=7*t,t) ▸ t=0.28947 and x=2.0263 and y=1.8421 and z=2.0263

   Dvs. koordinaterne for F er (2,026;1,842;2,026)

3. Vinklen mellem planerne findes ud fra vinklen mellem deres normalvektorer. Planen β har ligningen: 7x + 4y + 7z = 21. Normalvektoren til β aflæses af denne ligning til (7,4,7). Denne oprettes som vektoren m:

   m:=[7,4,7] ▸ [7,4,7]

   Planen α har som før nævnt normalvektoren n = (7,-4,7). Heraf finder man vinklen mellem normalvektorerne ved hjælp af ligningen for vinklen mellem to vektorer, der løses med hensyn til vinklen x:

   solve(cos(x*1.°)=dotP(n,m)/(norm(n)*norm(m)),x)|0<x<180 ▸ x=44.0034

   Det fremgår af tegningen, at man søger den stumpe vinkel mellem planerne, så vinklen mellem dem bliver 180° - 44° = 136°

Angående a): Enhver ligning på formen k·(7x - 4y + 7z - 21) = 0, hvor k∈R vil være rigtigt svar.

Angående c): x*1.° betyder, at der regnes i grader, selvom Ti-Nspire er indstillet til radianer.

Svar på opgave 13:

1. Væksthastigheden er dM/dt og findes ved at indsætte de oplyste værdier for t og M på højre side i ligningen.

   Det giver væksthastigheden: 50 - 5·1 - 0,086·45,5 mg/døgn = 41,09 mg/døgn

2. Man finder M(t) ved hjælp af følgende kommando:

   deSolve(m'=50-5*t-0.086*m and m(0)=0,t,m) ▸ m=−58.140*(0.91759)^t*((t-21.628)*(1.0898)^t+21.628)

   Dvs. M(t) = −58.140·(0,91759)^t·((t-21,628)·(1,0898)^t+21,628) = −58,14·(t-21,63) − 1258·0,9176^t

   Grafen for M(t) tegnet (med x som uafhængig variabel istedet for t)

   

Svar på opgave 14:

1. Man opretter f(x):

   f(x):=4-(4.6^x+4.6^−x)/2 ▸ Udført

   Vinduets bredde er afstanden mellem nulpunkterne for f(x), dvs. de x, for hvilke f(x) skærer x-aksen. Nulpunkterne findes:

   solve(f(x)=0,x) ▸ x=−1.3521 or x=1.3521

   Dvs. bredden af vinduet er: |−1,3521 - 1,3521| m = 2,7 m

   Man finder det x, hvor f(x) har maksimum:

   fMax(f(x),x) ▸ x=0.

   Dvs. f(x) har maksimum på y-aksen, som det også fremgår af figuren. Man finder maksimum af f(x) ved at indsætte x = 0:

   f(0) ▸ 3.

   Dvs. højden af vinduet er 3 m

2. Arealet af vinduet er integralet af f(x) fra x = -1,3521 til x = 1,3521. Man får:

   Integral(f(x),x,−1.35214,1.35214) ▸ 5.741

   Dvs. vinduets areal er 5,741 m²

3. Parablen har ligningen g(x) = ax² + bx + c. Her kendes c, der skal være lig med 3, da c er parablens skæring med y-aksen.

   Desuden kendes b som er lig med 0, fordi parablen har toppunkt på y-aksen.

   Man finder a med følgende solve-kommando:

   solve(a*(1.35214)²+3=0,a) ▸ a=−1.64088

   Dvs. forskriften for parablen er −1,641·x² + 3