Svar på opgave 1:

1. Der gælder, at arealet af parallelogrammet er lig med den numeriske værdi af determinanten af vektor a og vektor b.

   Areal = |det(a,b)| = |5·6 - 3·4| = 18

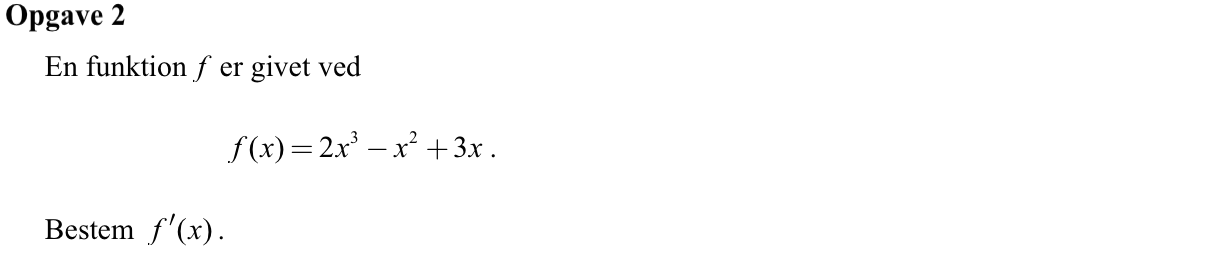
Svar på opgave 2:

1. Man får differentialkvotienten: f´(x) = 6x² - 2x + 3

Svar på opgave 3:

1. Tallet 124 er den årlige vækst, dvs det tal der skal lægges til sidste års mælkeydelse for at få dette års ydelse.

   Tallet 4783 er startværdien, dvs. mælkeydelsen for t = 0, dvs. år 1975.

Svar på opgave 4:

1. Man skal bruge ligningen for tangenten gennem punktet (1,3) = (1,f(1)). Den er y = f´(1)(x - 1) + f(1) ⇒ y = f´(1)(x - 1) + 3. Her har man, at

   f´(x) = dy/dx = 2x + xy, hvilket for (x,y) = (1,3) giver: f´(x) = 2·1 + 1·3 = 5.

   Dvs. tangentens ligning er y = 5·(x - 1) + 3 ⇔ y = 5x - 2

Svar på opgave 5:

1. Man bruger substitutionen u = x² + 3, du = 2x·dx. Man får (idet x² + 3 > 0 for alle x):

   

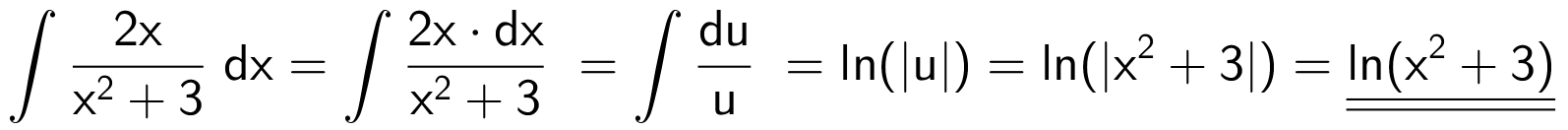
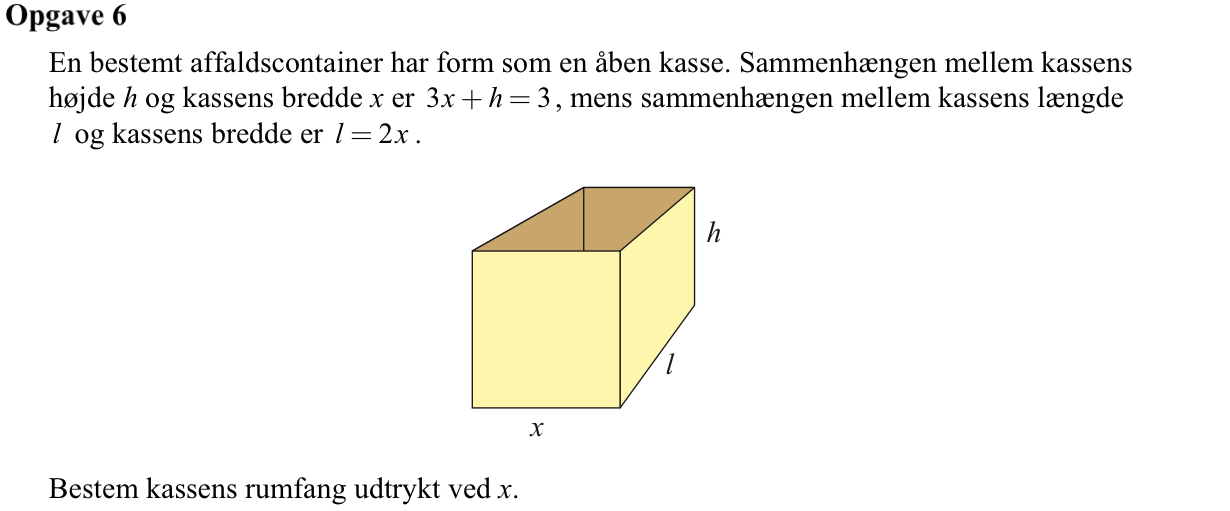
Svar på opgave 6:

1. Man isolerer h i udtrykket for sammenhængen mellem h og x: 3x + h = 3 ⇔ h = 3 - 3x.

   Rumfanget er x·l·h = x·(2·x)·(3 - 3x) = 6x² - 6x³

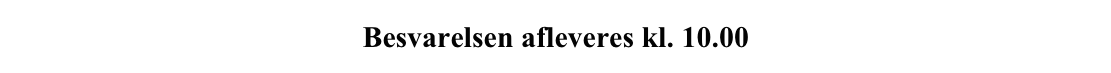
Svar på opgave 7:

1. Af forskriften for f(x) ses det, at der er tale om en potensfunktion. Man opretter derfor lister for L og V og foretager en potensregression.

   liste_l:={50,60,70,80,90,100,105} ▸ {50,60,70,80,90,100,105}

   liste_v:={1.29,2.19,3.47,5.11,7.45,10.36,12.05} ▸ {1.29,2.19,3.47,5.11,7.45,10.36,12.05}

   (Potensregression findes i Ti-Nspire under menuen Beregninger ▸ Statistik ▸ Statistiske beregninger ▸ Potens regression..., hvorefter man vælger de lister, der er oprettet for L og V).

   PowerReg liste_l,liste_v,1: CopyVar stat.RegEqn,v: stat.results ▸
   [["Titel","Potensregression"]
   ["RegEqn","a*x^b"]
   ["a",0.0000095]
   ["b",3.015812]
   ["r²",0.9996973]
   ["r",0.9998486]
   ["Resid","{...}"]
   ["ResidTrans","{...}"]]

   Heraf ses at a = 3,0158 og b = 0,0000095

   (Det bemærkes at a og b bruges i modsat betydning i Ti-Nspire i forhold til hvordan de bruges i opgaven).

   Som det fremgår af kommandoen PowerReg liste_l,liste_v,1: CopyVar stat.RegEqn,v: stat.results er det valgt at sætte regressionens navn lig med v. Man kan få regressions funktionen frem ved at skrive v(l) og trykke Enter i Ti-Nspire som vist:

   v(l) ▸ 0.0000095*l^3.015812

2. Man skal beregne V(87) for finde vægten af laksen.

   v(87) ▸ 6.742866

   Dvs. vægten af en laks med længden 87 cm 6,7 kg

   For at finde længden skal man løse ligningen V(x) = 2,56.

   solve(v(l)=2.56,l) ▸ l=63.10341

   Dvs. længden af en laks, der vejer 2,56 kg er 63,1 cm

3. Man skal bruge formlen for procent-procent vækst for potensfunktioner. Den giver:

   (1.25^3.015812-1)*100 ▸ 96.00285

   Dvs. når laksens længde øges med 25% øges vægten med 96 %

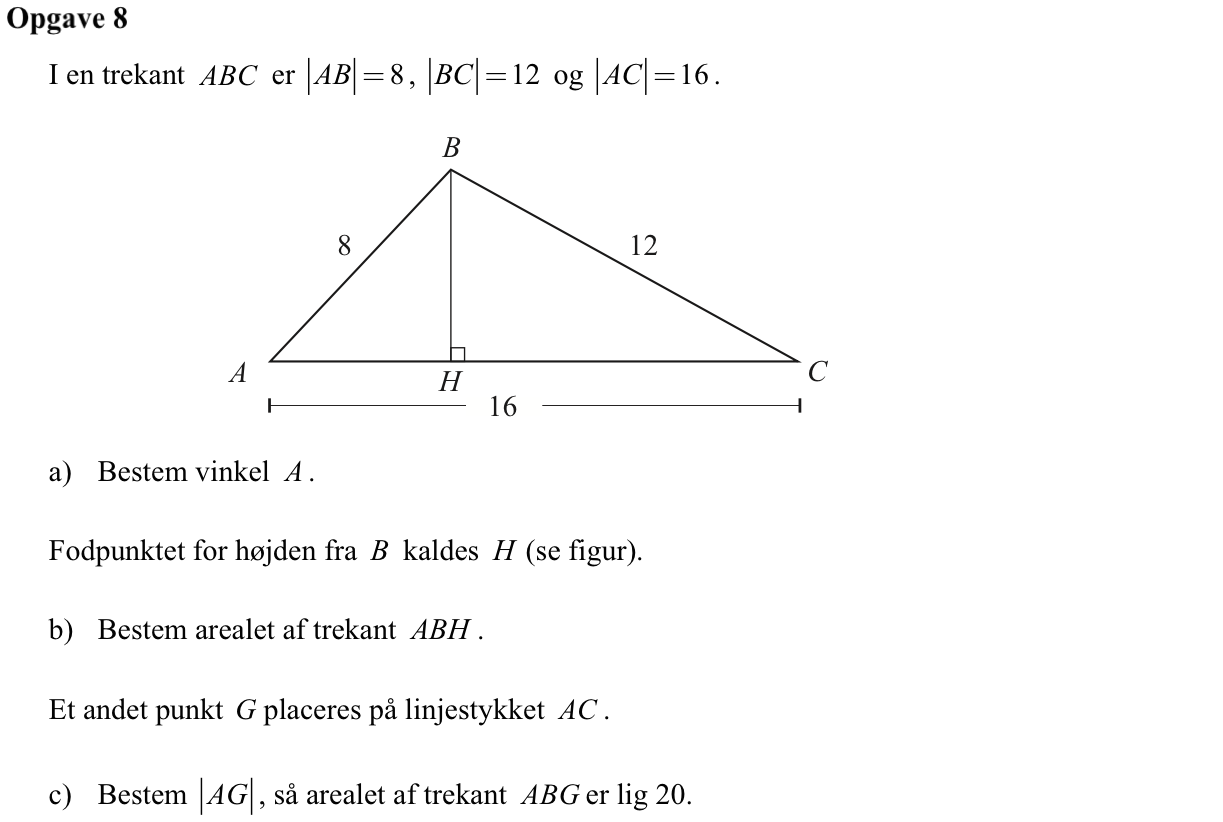
Svar på opgave 8:

1. Man kender alle sider i trekanten og finder ∠A ved hjælp af en cosinusrelation:

   solve(cos(x*1.°)=(8²+16²-12²)/(2*8*16),x)|0<x<180 ▸ x=46.56746

   Dvs. ∠A = 46,6°

2. Arealet af trekant ABH er 0,5·(højden i B)·|AH|. Højden i B = 8·sin(∠A), mens |AH| = 8·cos(∠A). Man får:

   0.5*8*cos(46.567°)*8*sin(46.567°) ▸ 15.97607

   Dvs. arealet af trekant ABH er 16,0

3. Arealet af trekant ABG er 0,5·(højden i B)·|AG| = 0,5·cos(∠A)·|AG|.

   Man sætter |AG| = x og skal løse ligningen: 0,5·[8·sin(46.567°)]·x = 20. Det giver

   solve(0.5*8*sin(46.567°)*x=20,x) ▸ x=6.885356

   Dvs. |AG| = 6,89

Svar på opgave 9:

1. Man opretter lister med data for de to typer pølser i Ti-Nspire:

   oksekødspølser:={111,131,132,149,149,153,157,158,184,190} ▸ {111,131,132,149,149,153,157,158,184,190}

   kyllingepølser:={86,94,102,132,135,142,143,144,146,152} ▸ {86,94,102,132,135,142,143,144,146,152}

   Man opretter to boksplot i Ti-Nspire:

   

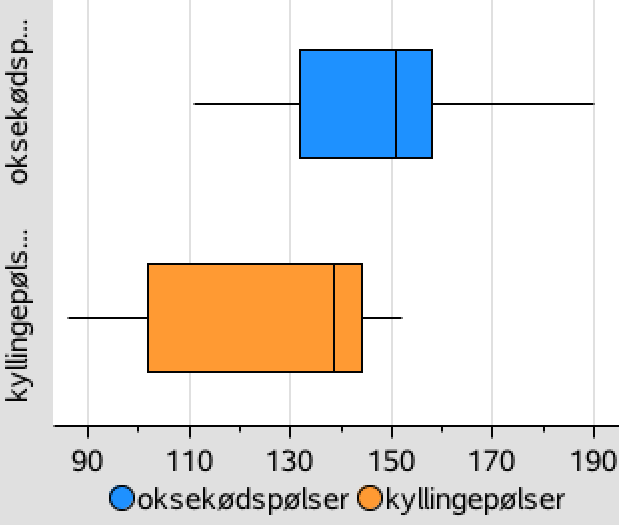
   Boksplottene viser, at kvartilsættet for kalorieindholdet i oksekødspølser er højere end kvartilsættet for kyllingepølser. Dvs. kalorieindholdet er generelt højere i oksekødspølser.

Svar på opgave 10:

1. Man opretter N(t) i Ti-Nspire:

   n(t):=b*a^(t) ▸ Udført

   For at bestemme a og b skal man løse de sammenhørende ligninger N(10) = 110 og N(30) = 160 med hensyn til a og b. Det gøres i Ti-Nspire:

   solve(n(10)=110 and n(30)=160.,a,b)|a>0 ▸ a=1.018911 and b=91.20718

   Dermed er forskriften: N(t) = 91,21·1.019^t

2. Man skal beregne N(5) og får følgende i Ti-Nspire:

   n(5)|a=1.018911 and b=91.20718 ▸ 100.1637

   Dvs. efter 5 sekunder var antallet af inficerede computere 100

   Fordoblingstiden findes af formlen: ln(2)/ln(a):

   ln(2)/ln(1.018911) ▸ 36.99861

   Dvs. fordoblingstiden er 37 sekunder

Svar på opgave 11:

1. Funktionerne oprettes i Ti-Nspire:

   g(x):=4*(1-exp(−x)) ▸ Udført

   h(x):=exp(x)-1 ▸ Udført

   Man får følgende graf i Ti-Nspire:

   

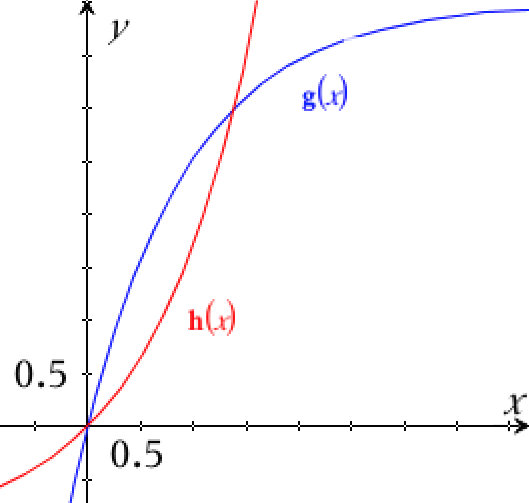
   Man finder x-værdierne for skæringspunkterne for graferne ved at løse ligningen g(x) = h(x) med hensyn til x i Ti-Nspire:

   solve(g(x)=h(x)*1.,x) ▸ x=0. or x=1.386294

   Dvs. førstekoordinaterne til skæringspunkterne for graferne af g og h er x = 0 eller x = 1,386

2. Arealet af M er integralet af g(x) - h(x) mellem x-værdierne af skæringspunkterne af de to grafer. Det giver følgende i Ti-Nspire:

   integral(g(x)-h(x),x,0,1.386294) ▸ 0.9314718

   Dvs. arealet af M er 0,931

3. g´(x) findes i Ti-Nspire:

   derivative(g(x),x) ▸ 4*exp(−x)

   Dvs. g´(x) = 4·e^-x

   Denne funktion er positiv for alle x da e^-x er en eksponentialfunktion og dermed altid positiv.

Svar på opgave 12:

1. Man opretter punkterne C og P som stedvektorer i Ti-Nspire:

   c:=[0,0,5] ▸ [0,0,5]

   p:=[2,−1,3] ▸ [2,−1,3]

   Man opretter dernæst vektoren CP:

   cp:=p-c ▸ [2,−1,−2]

   Denne vektor er en radius til kuglen. Vektorens længde er lig med radius i kuglen:

   radius:=norm(cp) ▸ 3

   Dvs. kuglens radius er 3 og den har centrum i C = (0,0,5). Dermed er dens ligning: (x - 0)² + (y - 0)² + (z - 5)² = 3² ⇒ x²+y²+(z-5)²=3²

   Vektor CP er normalvektor til tangentplanen i P, da en radiusvektor fra P til centrum af kuglen står vinkelret på tangentplanen i P.

   Tangent planen kan nu fastlægges, da man kender et punkt i planen og en normalvektor.

   Om et vilkårligt punkt X = (x,y,z) i planen gælder: PX·CP = 0. Man opretter først PX i Ti-Nspire:

   px:=[x,y,z]-p ▸ [x-2,y+1,z-3]

   Dernæst beregner man skalarproduktet PX·CP og sætter det lig med nul.

   dotP(cp,px)=0 ▸ 2*x-y-2*z+1=0

   Dvs. tangentplanens ligning er 2x - y - 2z + 1 = 0

2. Q har den egenskab at dens afstand til C = 3, dvs. længden (normen) af vektor CQ er 3. Desuden opfylder Q's koordinater ligningen for planen β. Man løser disse ligninger i Ti-Nspire med hensyn til x, y og z:

   solve((norm(cx))²=9 and 3*x+6*y-6*z+3=0,x,y,z) ▸ x=1 and y=2 and z=3

   Dvs Q's koordianter er (x,y,z) = (1,2,3)

   (Bemærk at man er nød til at skrive "(norm(cx))²=9" for at få solve-kommandoen til at virke. "norm(cx)=3" virker ikke).

Svar på opgave 13:

1. Væksthastigheden til t=10 er ifølge differentialligningen lig med 0,82·0,88¹⁰·N(10) = 0,82·0,88¹⁰·266 = 60,75

2. Man bruger desolve-kommandoen til at løse differentialligningen med startbetingelsen N(10) = 266:

   deSolve(n'=0.82*(0.88)^t*n and n(10)=266,t,n) ▸ n=1587.584*(0.0016375)^(0.88)t

   Dvs. N(t) = 1587,6·0,001638^0,88t mio.

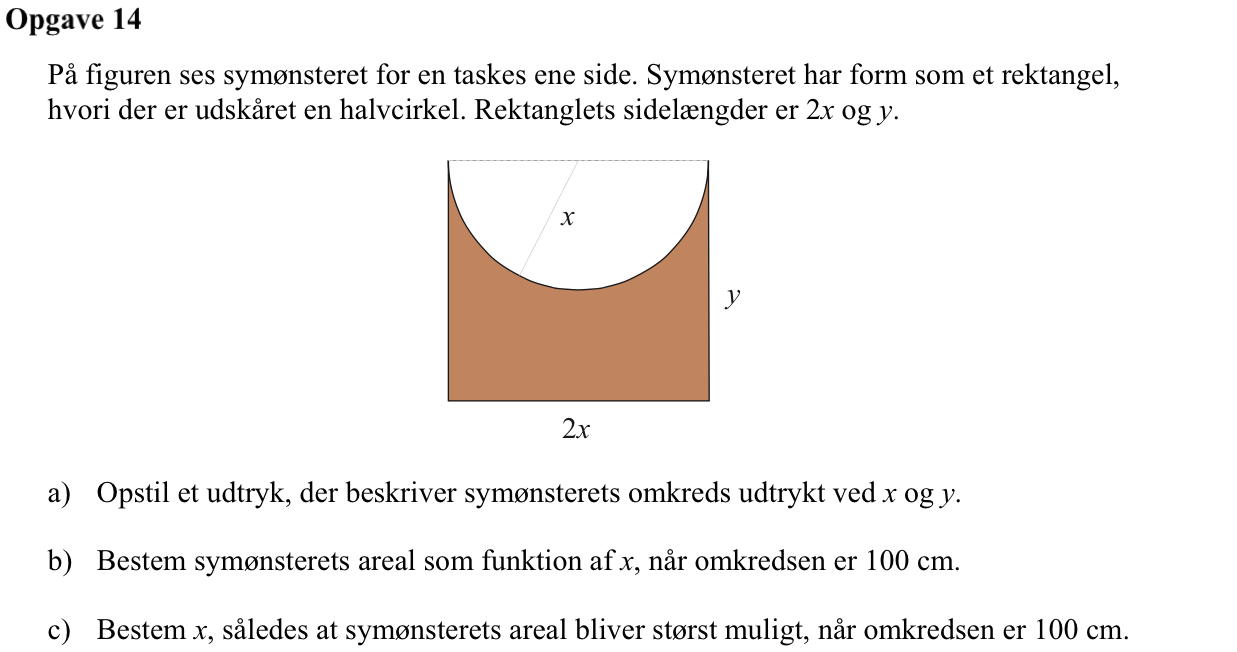
Svar på opgave 14:

1. Omkredsen = 2x + 2y + π·x = (π+2)x + 2y

2. Man finder y som funktion af omkreds = 100 og x: 100 = (π+2)x + 2y ⇒ y = 50 − (0,5π + 1)·x

   Arealet af figuren er 2·x·y - (π·x²)/2. Man indsætter udtrykket for y og får:

   Arealet = 2·x·(50 − (0,5π + 1)·x) - (π·x²)/2 = 100·x - (3·π/2 + 2)·x²

3. Man opretter arealet som en funktion af x i Ti-Nspire:

   areal(x):=100*x-(3*π/2+2)*x² ▸ Udført

   Man finder det x, som giver det største areal ved hjælp af fMax-kommandoen i Ti-Nspire:

   fMax(areal(x)*1.,x) ▸ x=7.448913

   Dvs. det x, som giver det største areal for symønstret, er x = 7,45