Svar på opgave 1:

1. Løsning:

   x² + x - 12 = 0 ⇔

   x = -1/2 ± (1/2)·√[1+4·12] ⇔

   x = -1/2 ± (1/2)·√49 ⇔

   x = -1/2 ± (1/2)·7 ⇔

   x = -1/2 - 7/2 ∨ x = -1/2 + 7/2 ⇔

   x = −4 ∨ x = 3

Svar på opgave 2:

1. Vektorerne a og b er ortogonale, når de er egentlige, og når a·b = 0.

   De egentlige, da de hver har en koordinat, der er en konstant forskellig fra 0. Man får for skalarproduktet:

   a·b = 0 ⇒ (2,t+1)·(t-1,3) = 0 ⇔ 5·t + 1 = 0 ⇔ t = −1/5

Svar på opgave 3:

1. Tallet 23 er startværdien (værdien til t = 0) og 1,386 er fremskrivningsfaktoren, som man skal gange antallet med hvert minut for at få det nye antal. (1,386 er også 1 + vækstraten.)

Svar på opgave 4:

1. Man skal indsætte f(x) i differentialligningen og gøre prøve, dvs. man skal vise, at f´(x) er lig med f(x) + x = e^x - 1. Man får:

   f'(x) = d/dx(e^x - x - 1) = e^x - 1.

   Dette vser, at f(x) er en løsning til differentialligningen.

Svar på opgave 5:

1. Man integrerer f(x) for at finde en vilkårlig stamfunktion til f. Denne kaldes F(x):

   F(x) = ∫f(x) dx = ln(x) + x² + k.

   Man skal nu finde det k, der gør, at F(1) = 3. Man får:

   F(1) = ln(1) + 1² + k = 3 ⇔ k = 3 - 1 = 2

   Dvs. stamfunktionen er F(x) = ln(x) + x² + 2

Svar på opgave 6:

1. På grafen ses, hvornår f´(x) er mindre end henholdsvis større end 0.

   

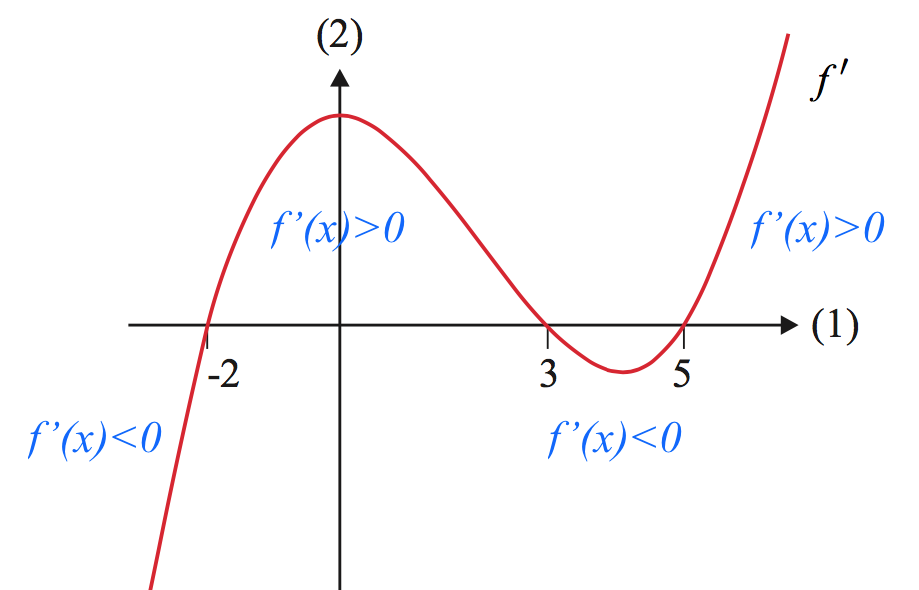
   Af dette fremgår det, at monotoniforholdene for f er:

   -3<x<-2 f er aftagende (f´<0)

   -2<x<3 f er voksende (f´>0)

   3<x<5 f er aftagende (f´<0)

   x>5 f er voksende (f´>0)

Svar på opgave 7:

1. Man opretter lister med faldhøjde og antal fald:

   faldhøjde:={1.7,2.,2.9,4.1,5.6,6.3,7.,8.,10.,13.9} ▸ {1.7,2.,2.9,4.1,5.6,6.3,7.,8.,10.,13.9}

   antal_fald:={42,21,10.3,6.9,5.1,4.8,4.4,4.1,3.7,3.2} ▸ {42,21,10.3,6.9,5.1,4.8,4.4,4.1,3.7,3.2}

   Man laver en potensregrssion på de to lister:

   PowerReg faldhøjde,antal_fald,1: CopyVar stat.RegEqn,f1: stat.results ▸
      [["Titel","Potensregression"]
      ["RegEqn","a*x^b"]
      ["a",46.2171]
      ["b",−1.1543]
      ["r²",0.897823]
      ["r",−0.947535]["Resid","{...}"]
      ["ResidTrans","{...}"]]

   Heraf ses, at a = −1,1543 og b = 46,2171

   (Det bemækes at Ti-Nspire bruger a og b modsat opgaven).

2. Man skal finde det x for hvilket f(x) = 15. Man bruger regressionsfunktionen f1(x), som Ti-Nspire har fundet:

   solve(f1(x)=15,x) ▸ x=2.65085

   Dvs. faldhøjden er 2,65, når det gennemsnitlige antal fald er 15.

3. Man bruger formlen for procent-procent vækst og får: (1 + r_y) = (1 + r_x)^a ⇒ r_y = (1 + r_x)^a - 1, hvor r_y er ændringsprocenten for antal fald og r_x er ændringsprocenten til faldhøjden. Det giver for r_y:

   (1.5^−1.1543-1)*100 ▸ −37.3764

   Dvs. antal fald aftager med 37,4 %

Svar på opgave 8:

1. Man opretter lister med mængde og antal kunder. (Start med nedre grænse for første interval og derefter øvre grænse for alle intervaller inklusive første).

   mængde:={0,10,20,30,40,50,60} ▸ {0,10,20,30,40,50,60}

   antal_kunder:={0,10,23,16,21,10,9} ▸ {0,10,23,16,21,10,9}

   Man beregner frekvenser for kunder ved at dividere med summen af antal kunder:

   frekvens_kunder:=antal_kunder*1./sum(antal_kunder) ▸ {0.,0.11236,0.258427,0.179775,0.235955,0.11236,0.101124}

   Man beregner kumulerede frekvenser ved at lægge frekvenser sammen styk for styk:

   kum_frekv_kunder:=cumulativeSum(frekvens_kunder) ▸ {0.,0.11236,0.370787,0.550562,0.786517,0.898876,1.}

   Man tegner en sumkurve i Ti-Nspire:

   

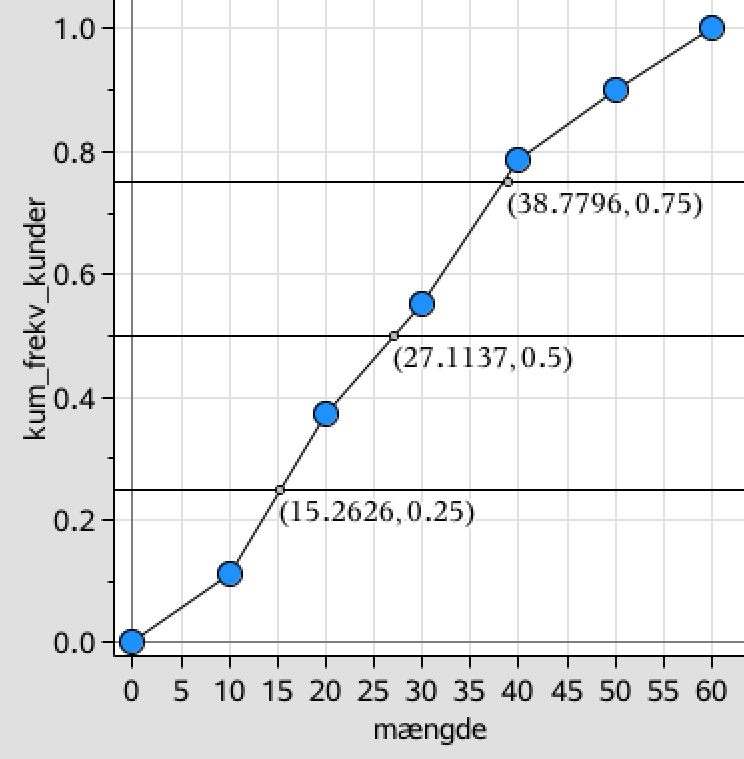
   Kvartilerne beregnes ved at finde de steder, hvor sumkurven skærer linjerne for kumulereret frekvens = 0,25; 0,50 henholdsvis 0,75.

   Disse tal aflæses:

   nedre kvartil (25%-kvartil) = 15,3 l

   anden kvartil eller median (50%-kvartil) = 27,1 l

   øvre kvartil (75%-kvartil) = 38,8 l

Svar på opgave 9:

1. Som det fremgår af nedenstående figur, er s en katete i en retvinklet trekant og tan(40,7°) = 2,7/s.

   

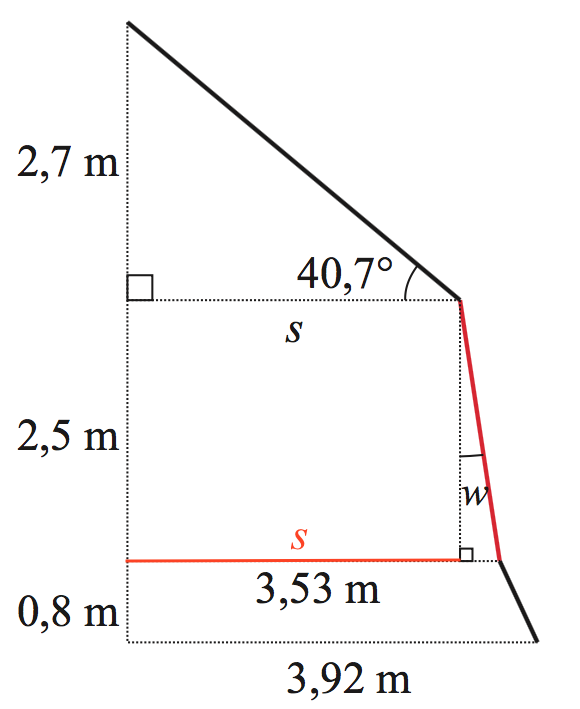
   Man får:

   solve(tan(40.7°)=2.7/s,s) ▸ s=3.13904

   Dvs. s = 3,14

   Af figuren fremgår endvidere, at w er en vinkel i en anden retvinklet trekant, hvor den modstående katete til w er 3,53 - s = 3,53 - 3,13904 = 0,39096. Man får følgende ligning for w:

   solve(tan(w*1.°)=0.39096/2.5,w)|0<w<90 ▸ w=8.88815

   Dvs. w = 8,9°

2. Ottekanten består af otte ligebenede trekanter. Hver trekant har arealet 0,5·højde·grundlinje = 0,5·(3,92·sin(v))·3,0. Her v lig med grundvinklen til trekanten.

   Denne vinkel er halvdelen af hjørnevinklen i en regulær ottekant, som er (8·180° - 360°)/8 = 180° - 45° = 135°. Dvs. v = 135°/2 = 67,5°. Vinklerne er vist nedenunder.

   

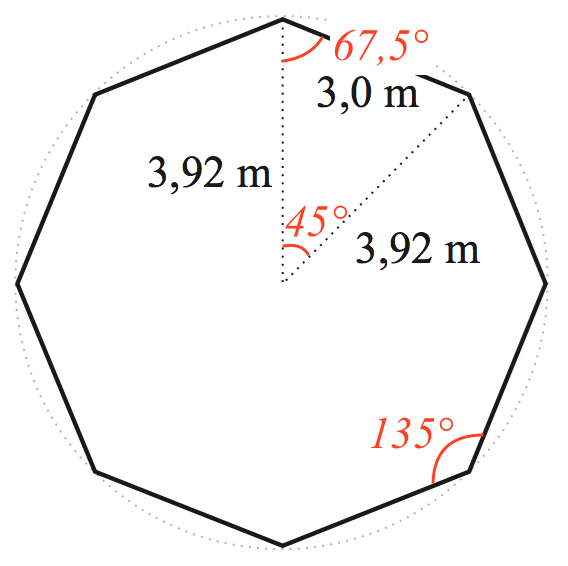
   Arealet af ottekanten er dermed 8·0,5·3,92·sin(67,5°)·3 = 43,5

Svar på opgave 10:

1. Man bruger afstandsformlen mellem punkt og plan. Punktet har koordinaterne: (0,0,20). Planen har ligningen: 1x + 0y + 3z + 20 = 0

   Afstanden er |1·0 + 0·0 + 3·20 + 20|/√[1² + 0² + 3²] = 25,30 meter

2. Man finder vinklen mellem de to flader ud fra deres normalvektorer. Normalvektoren til α kaldes m og aflæses af αs ligning : 1x + 0y + 3z + 20 = 0, dvs. m = (1,0,3).

   Normalvektoren (eller rettere en normalvektor) til sidefladen, der indeholder C,D og T, findes ved hjælp af krydsproduktet mellem vektorerne TC og TD.

   Man opretter de nævnte vektorer:

   m:=[1,0,3] ▸ [1,0,3]

   tc:=[−20,20,0]-[0,0,20] ▸ [−20,20,−20]

   td:=[−20,−20,0]-[0,0,20] ▸ [−20,−20,−20]

   Man finder krydsproduktet af TC og TD:

   crossP(tc,td) ▸ [−800,0,800]

   Dette divideres med 800 for at få mindre koordinater:

   n:=[−800,0,800]/800 ▸ [−1,0,1]

   Normalvektorerne indsættes i formlen for vinklen mellem to vektorer:

   solve(cos(x*1.°)=dotP(m,n)/(norm(m)*norm(n)),x)|0<x<180 ▸ x=63.4349

   Dvs. vinklen mellem α og fladen, som indeholder punkter C, D og T er 63,4°

   (Man kan også få 180° - 63,4° = 116,6°, som er den stumpe vinkel mellem α og den plan, der indeholder C, D og T. For at afgøre, hvad, der er det rigtige, må man støtte sig til tegningen.)

3. Vektoren TF er lig med (20,20,0)-(0,0,20) = (20,20,−20) og proportional med retningsvektoren til linjen.

   Man vælger linjens retningsvektor til at være r = TF/20 = (1,1,-1).

   Parameterfremstilling for l er dermed l: (0,0,20) + t·(1,1,-1)

   Man opretter paramterfremstillingen som funktion af t:

   l(t) ▸ [t,t,20-t]

   Man skal finde det t, der gør at (x,y,z) = (t,t,20-t) opfylder α's ligning: 1x + 0y + 3z + 20 = 0 ⇒ 1·t + 0·t + 3·(20-t) + 20 = 0 ⇔ t = 40.

   Koordinaterne for skæringspunktet findes ved at indsætte t=40 i l(t):

   l(40) ▸ [40,40,−20]

   Dvs. skæringspunktet B er (40,40,-20)

Svar på opgave 11:

1. Arealet af M findes som integralet af f(x) - g(x) mellem skæringspunkter for graferne til f og g. Graferne er vist nedenunder.

   

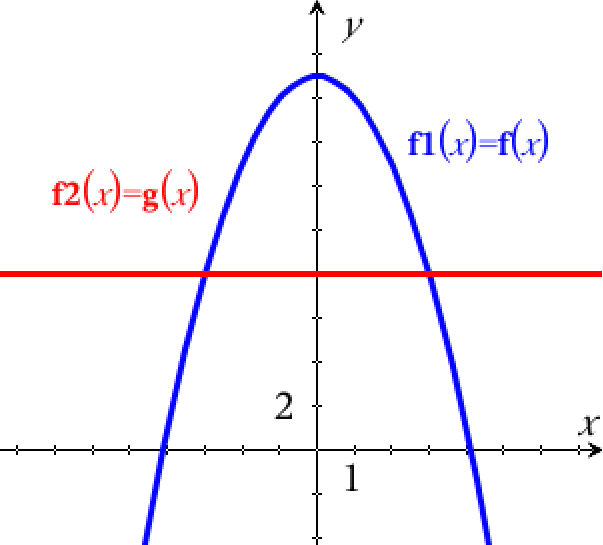
   Man opretter funktionerne:

   f(x):=17-x² ▸ Udført

   g(x):=8 ▸ Udført

   Førstekoordinaterne til skæringspunkterne mellem f og g findes:

   solve(f(x)=g(x),x) ▸ x=−3 or x=3

   Integralet beregnes:

   integral(f(x)-g(x),x,−3,3) ▸ 36

   Dvs. arealet af M er 36

2. Man bruger formlen for rumfanget af et omdrejningslegeme ved rotation om x-aksen:

   1.*π*integral(f(x)²-g(x)²,x,−3,3) ▸ 2623.86

   Dvs. rumfanget er 2623,9

   (Bemærk at man integrerer [f(x)² - g(x)²] og ikke [f(x) - g(x)]².)

Svar på opgave 12:

1. Man skal bestemme f(100) og opretter sínusfunktionen

   f(t):=6.61*sin(0.0167*t-1.303)+12.2 ▸ Udført

   Man indsætter t = 100:

   f(100) ▸ 14.5718

   Dvs. dagens længde er 14,6 timer 100 dage efter 1. januar.

2. En sinusfunktion antager sin største værdi (i intervallet 0<t<2π), når indholdet af funktionen er π/2. Dvs. størsteværdien antages for 0,0167·t - 1,303 = π/2. Man får:

   solve(0.0167*t-1.303=π/2,t) ▸ t=172.084

   Dvs. den længste dag er dag nummer 172 (21. juni).

   (Man kan også finde størsteværdien ved at differentiere og sætte lig med 0, men så skal man vælge mellem to ekstremumspunkter, hvor den ene er maksimum og den anden er minímum.)

3. Man beregner f´(100):

   derivative(f(t),t)|t=100 ▸ 0.103036

   Dvs. f´(100) = 0,103 timer/døgn

   Dette tal er det antal timer, som dagslængden vokser pr. døgn efter 100 døgn.

Svar på opgave 13:

1. Væksthastigheden findes ved at indsætte I(t) = 0,3 og løse ligningen med hensyn til I'(t):

   0,4·I'(t) + 10·0,3 = 9 ⇒ I'(t) = (9-10·0,3)/0,4 = 15.

   Dvs. ændringen i strømstyrke er 15 A/s

2. Forskriften for I(t) findes ved at løse differentialligningen med hensyn til I(t):

   deSolve(0.4*i'+10*i=9 and i(0)=0,t,i) ▸ i=0.9-0.9*exp(−25*t)

   Dvs. I(t) = 0,9·(1 - e^−25t)

Svar på opgave 14:

1. Tangentens ligning er y = f´(1)·(x - 1) + f(1).

   Man har: f´(x) = 2·(x-3)

   Man indsætter x=1 i f´(x) og f(x) for tangentens ligning:

   2·(1-3)·(x-1)+(1-3)² = 8-4x.

   Dvs. tangentens ligning er y = 8 - 4x

2. Man opretter funktionen g(x,a), der er forskriften for tangenten gennem P(a,f(a)):

   g(x,a):=fm(a)*(x-a)+f(a) ▸ Udført

   Q er punktet (0,g(0,a)), hvor g(0,a) er:

   g(0,a) ▸ −(a-3)*(a+3)

   Dvs. Q = (0,9-a²)

   R er punktet (x₀,0), hvor x₀ er nulpunktet til g(x,a) for 0<a<3. Man finder x₀:

   solve(g(x,a)=0,x)|0<a<3 ▸ x=(a+3)/2 and 0<a<3

   Dvs. R = ((a+3)/2,0)

3. Man opretter funktionen T(a):

   t(a):=0.25*(9-a²)*(a+3) ▸ Udført

   Man finder nulpunkterne for T'(a) for 0>a>3:

   solve(derivative(t(a),a)=0,a)|0>a>3 ▸ a=1.

   Dvs. T'(a) har nulpunkt for a = 1. Man undersøger værdien af T(a) i dette punkt og i yderpunkterne, som er a = 0 og a = 3:

   T(0) = 27/4 = 6,75

   T(1) = 8

   T(3) = 0

   Dvs. trekanten OQR har sit største areal for a = 1