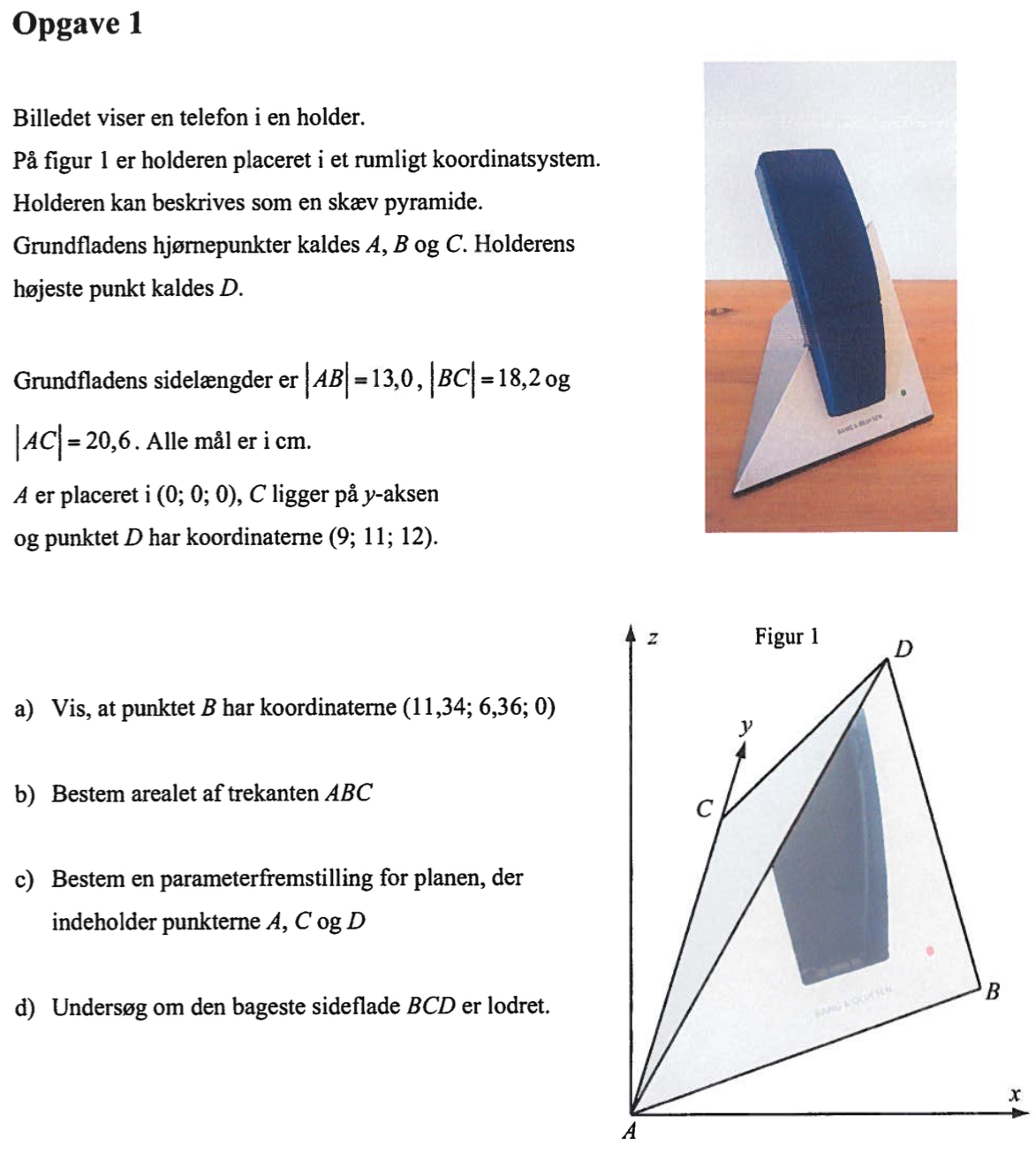
Svar på opgave 1:
Løst i Ti-Nspire.
-
Tegningen nedenunder er lavet i Geogebra. Den viser trekant ABC i xy-planen. Koordinaterne til B i xy-planen kaldes (xB,yB).
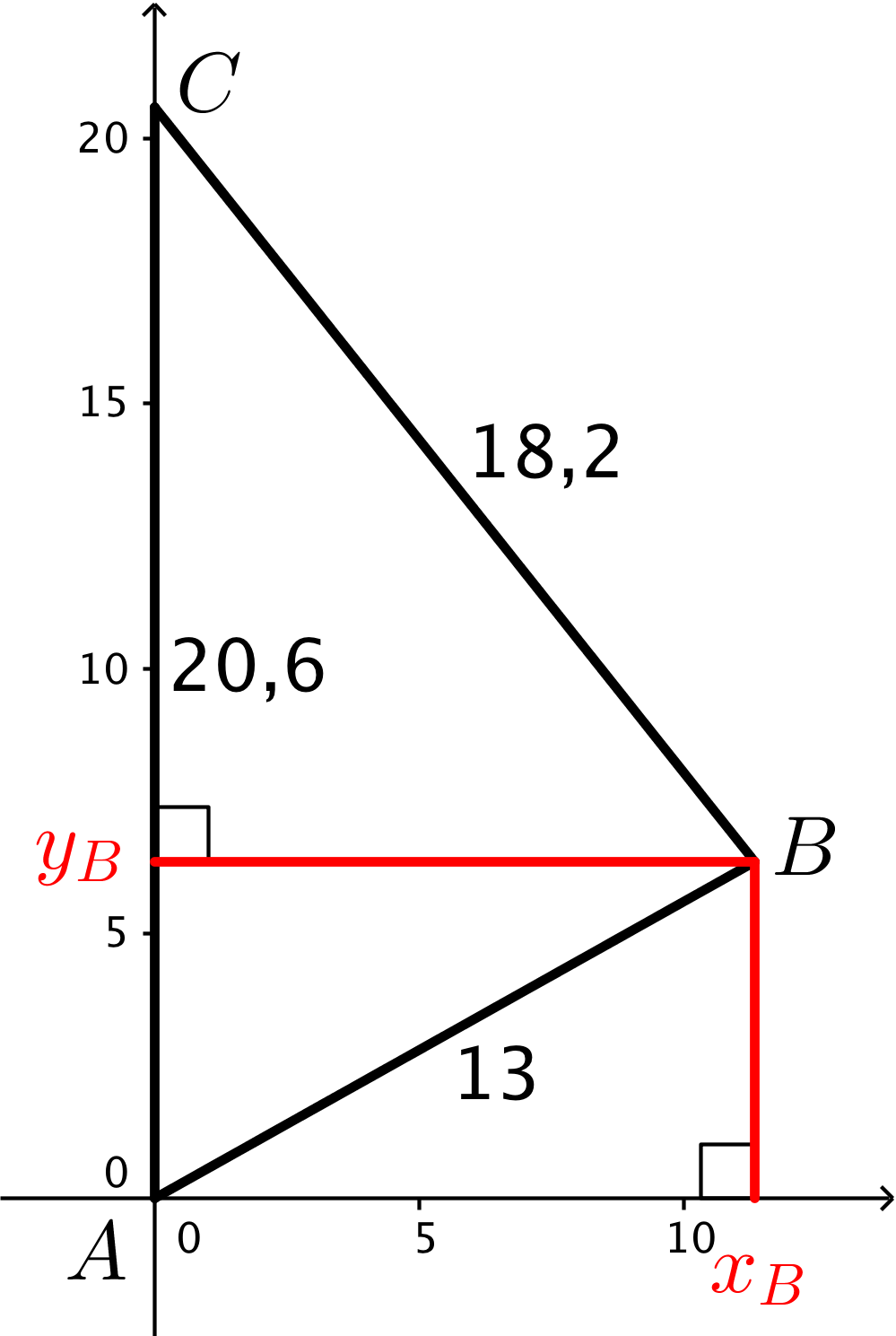
Det ses af figuren, at xB og yB kan findes ved hjælp af Pythagoras læresætning. Det gøres i Ti-Nspire:
solve((20.6-y)2+x2=(18.2)2 and y2+x2=(13.)2,x,y)|x>0 and y>0 ▸ x=11.3368 and y=6.3621
Dvs. da z-koordinaten til B er 0, får man, at B = (11,3;6,36;0)
-
Arealet af trekant ABC er 0,5·|AC|·xB = 0,5·20,6·11,34 = 116,8
-
Planens går gennem A = (0,0,0) og udspændes af vektorerne AB og AC. Dens parameterfremstilling kan skrives:
(x,y,z) = s·AB + t·AC = s·(11,34;6,36;0) + t·(0;20,6;0)
-
Hvis sidefladen ACD er lodret, vil en normalvektor til den stå vinkelret på en normalvektor til xy-planen.
En normalvektor til sidefladen er krydsproduktet af vektor BC = (−11,34;14,24;0) og BD = (−2,34;4,64;12). Dette giver i Ti-Nspire:
bc:=[−11.34,14.24,0] ▸ [−11.34,14.24,0]
bd:=[−2.34,4.64,12] ▸ [−2.34,4.64,12]
crossP(bc,bd) ▸ [170.88,136.08,−19.296]
Hernæst benytter man, at xy-planen har normalvektoren (0,0,1). Man finder skalarproduktet af normalvektorerne til sidefladen og xy-planen:
dotP([170.88,136.08,−19.296],[0,0,1]) ▸ −19.296
Da dette skalarprodukt er forskelligt fra 0, står sidefladen ikke vinkelret på xy-planen og den er dermed ikke lodret
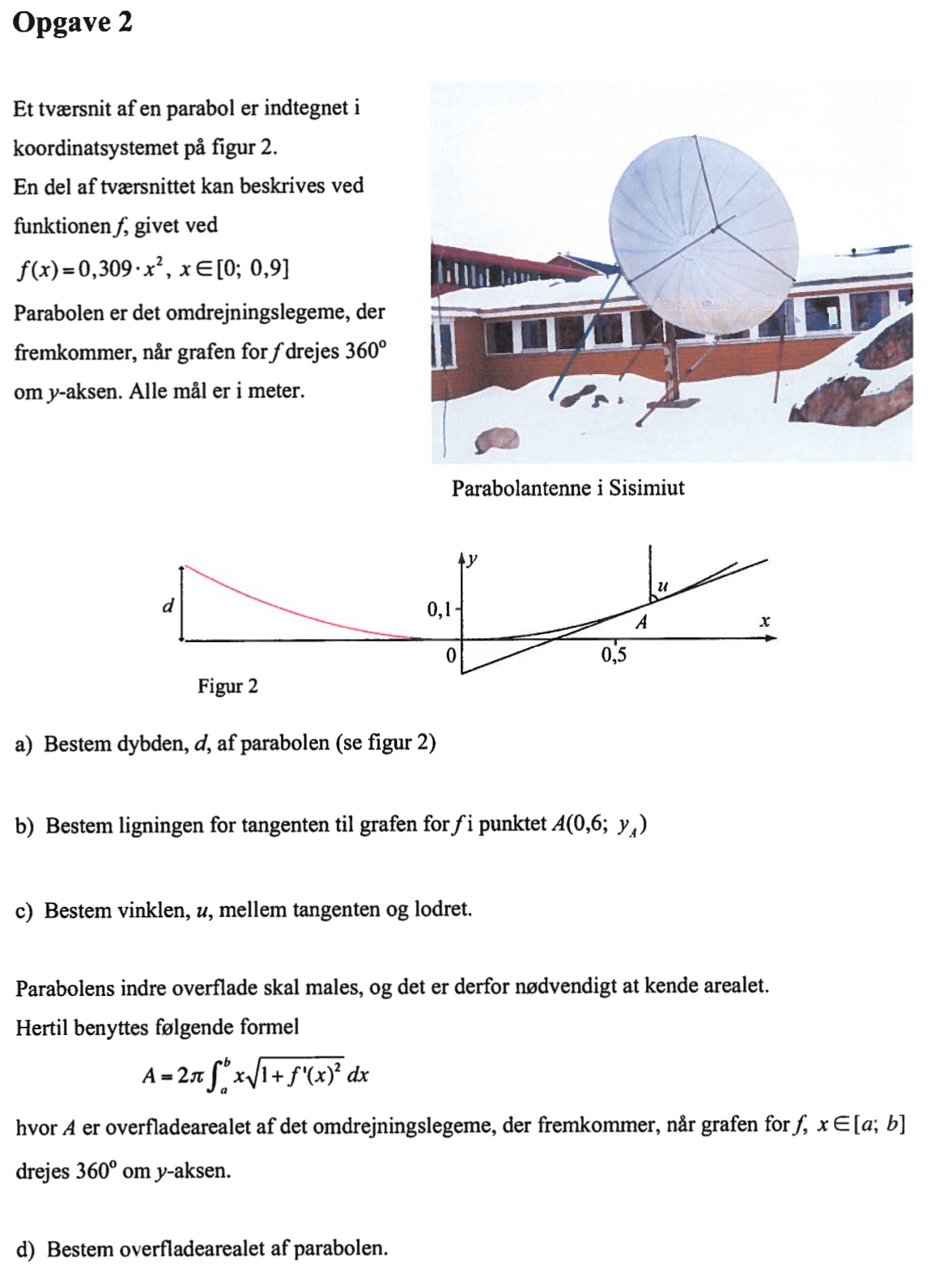
Svar på opgave 2:
-
Man opretter f(x) i Ti-Nspire:
f(x):=0.309*x2 ▸ Udført
Dybden d findes som f(0,9) i Ti-Nspire:
f(0.9) ▸ 0.25029
Dvs. d = 0,25
-
Man bruger kommandoen tangentLine i Ti-Nspire. Man kan som her sætte "y=" foran kommandoen for syns skyld:
y=tangentLine(f(x),x,0.6) ▸ y=0.3708*x-0.11124
Dvs. tangentens ligning i punktet (0,6;yA) = (0,6;f(0,6)) er: y = 0,371·x - 0,111
-
Tangens til vinklen mellem tangenten og vandret er 0,3708, som er hældningen til tangenten. Denne vinkel, kaldet x, findes i Ti-Nspire ved at løse ligningen tangens(x) = 0,3708 (for 0<x<90°):
solve(tan(x*1.°)=0.3708,x)|0<x<90 ▸ x=20.3448
Vinklen u er 90° minus denne vinkel:
90-20.3448 ▸ 69.6552
Dvs. vinklen u = 69,7°
-
Man indsætter f(x) = 0,309·x2, a = 0 og b = 0,9 i formlen og beregner arealet i Ti-Nspire:
2*π*integral(x*sqrt(1+(derivative(f(x),x))2),x,0,0.9) ▸ 2.73237
Dvs. overfladearealet af parabolen er 2,73 m2
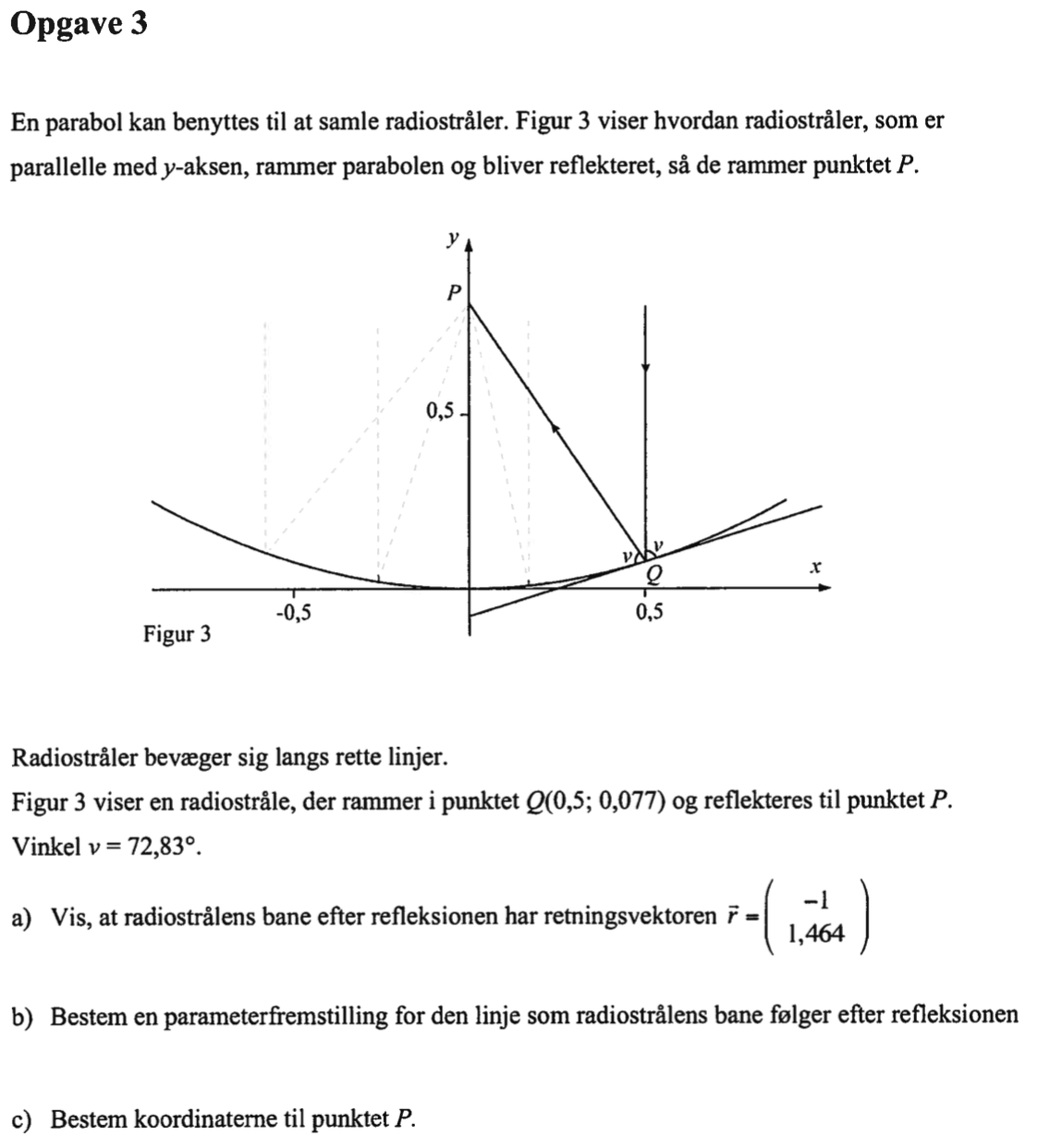
Svar på opgave 3:
-
Man skal kende vinklen mellem vandret og vektoren QP. Denne findes som w ud fra nedenstående tegning.
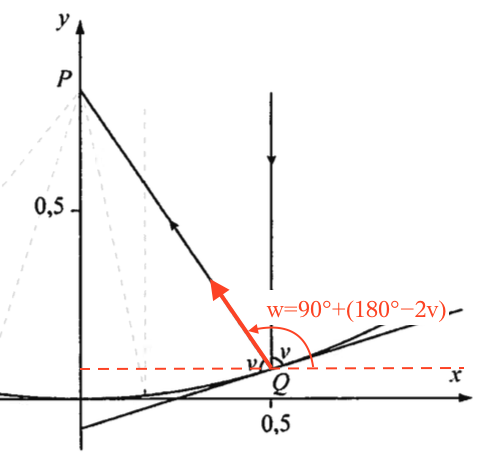
Man får at w = 90° + (180° - 2·72,83°) ▸ 124,34°. Dermed er QP = (cos(124,34°),sin(124,34°)) = (−0,5641;0,8257). Denne vektor er proportional med (−0,5641/0,5641;0,8257/0,5641) = (-1;1.464)
-
Lysstrålen er en halvlinje der starter i Q = (0,5;0,077) og som har retningsvektoren r = (-1;1,464). Parameterfremstillingen for lysstrålen l er
l: (1;−1,46375)·t + (0,5;0,077), hvor t>0
-
Man skal finde det t i parameterfremstillingen for l der giver skæringspunktet for l med y-aksen. Dette punkt har x-koordinaten 0, dvs. man skal løse ligningen x(t) = 0 ⇒ t + 0,5 = 0 ⇒ t = -0,5. Dette t indsættes i parameterfremstillinge for l og man får:
P = l(0,5) = (1;−1,464)·0,5 + (0,5;0,077) = (0;0,809)

Svar på opgave 4:
-
Differentialligninge løses ved hjælp af desolve-kommandoen i Ti-Nspire (T kaldes y, da Ti-Nspire ikke skelner mellem store og små bogstaver):
deSolve(y'=−k*(y-yr),t,y) ▸ y=c1*exp^(−k*t)+yr
Dvs. løsningen er T(t) = Tr - b·e−k·t
(Hvis Tr > T fra starten og b er positiv vil det betyde, at temperaturen nærmer sig Tr mere og mere med tiden nede fra).
-
Nedenstående graf er tegnet i Geogebra.
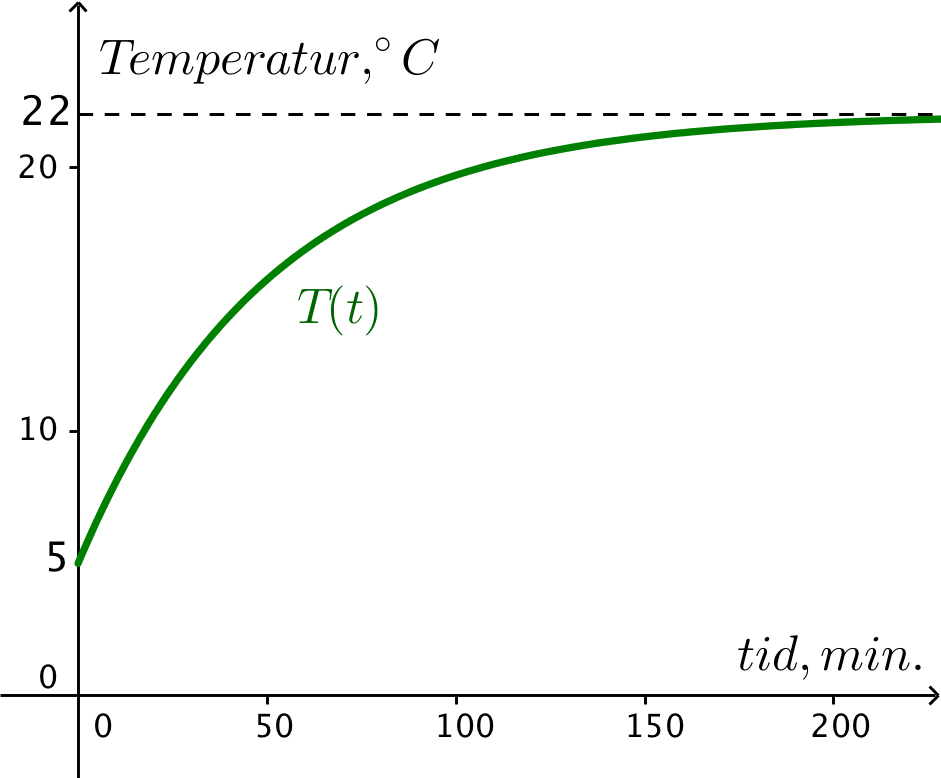
-
Når k mindskes med 20 % bliver dens værdi: 0,02·0,8 = 0,016. Man skal løse ligningen 22 - 17·e−0,016·t = 15
solve(22-17*exp(−0.016*t)=15,t) ▸ t=55.4564
Dvs. væskens temperatur kan holde sig under 15 °C i 55,5 min.

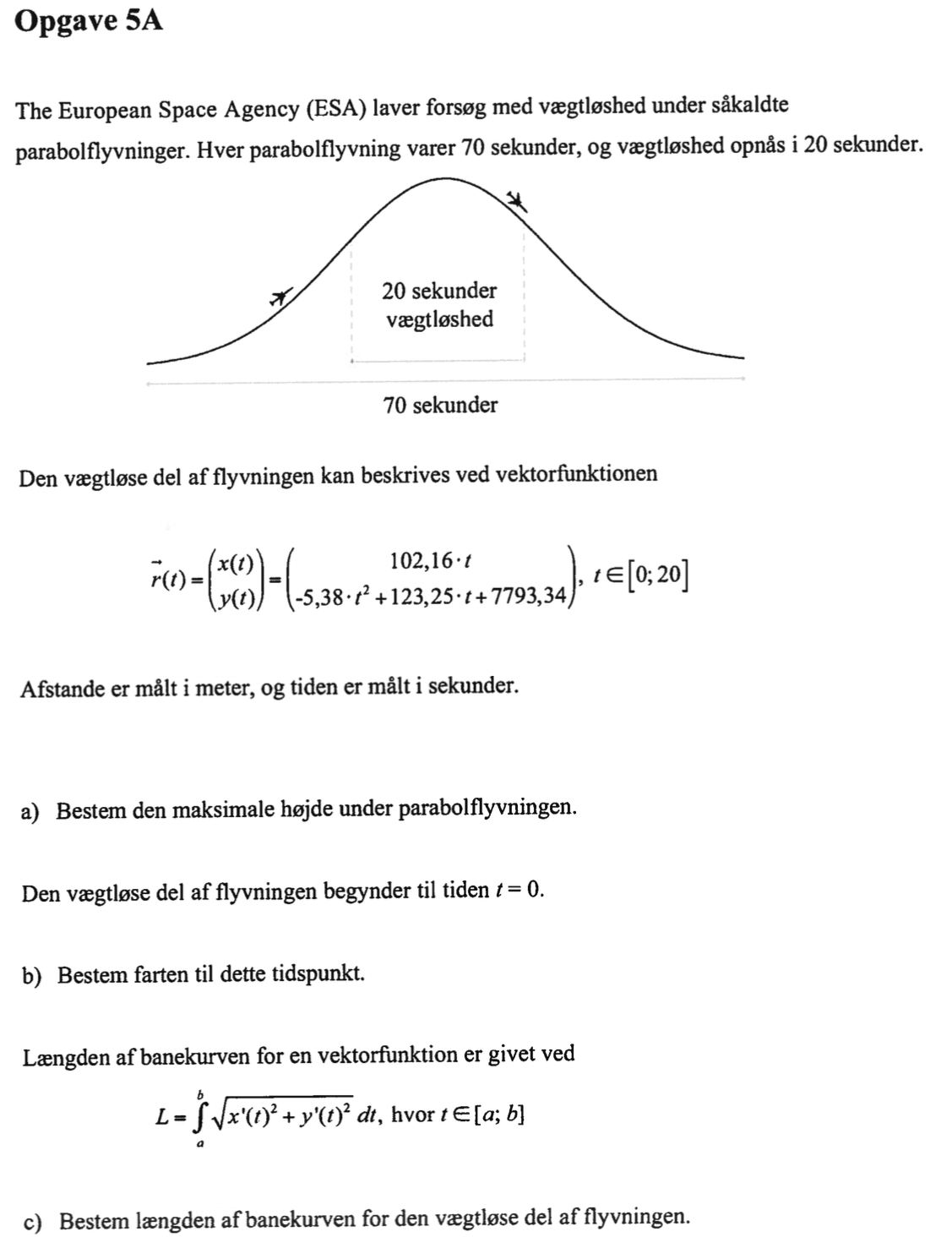
Svar på opgave 5a:
-
Den maksimale højde fås når y(t) = −5,38·t2 + 123,25·t + 7793,34 er størst. Dette maksimum beregnes i Ti-Nspire ved først at finde det t som giver den største y(t) og dernæst indsætte dette t i y(t):
fMax(−5.38*t2+123.25*t+7793.34,t) ▸ t=11.4545
−5.38*t2+123.25*t+7793.34|t=11.4545 ▸ 8499.22
Dvs. den maksimale højde for parabolflyvningen er 8499 m
-
Farten findes ved at beregne længden af vektoren (x'(t),y'(t)), når t = 0. Man får:
x'(t) = 102,16 m/s, y'(t) = 23,25 - 10,76·t
Farten er derfor for t = 0:
√[102,162 + (23,25 - 10,76·0)2] m/s = √[102,162 + 23,252] m/s = √[10436,7 + 15190,6] m/s = 160,1 m/s
-
Længden af kurven findes ved at indsætte x'(t), y'(t), a = 0 og b = 20.
integral(sqrt((102.16)2+(123.25-10.76*t)2),t,0,20) ▸ 2391.14
Dette giver, at kurvens længde er 2391 m
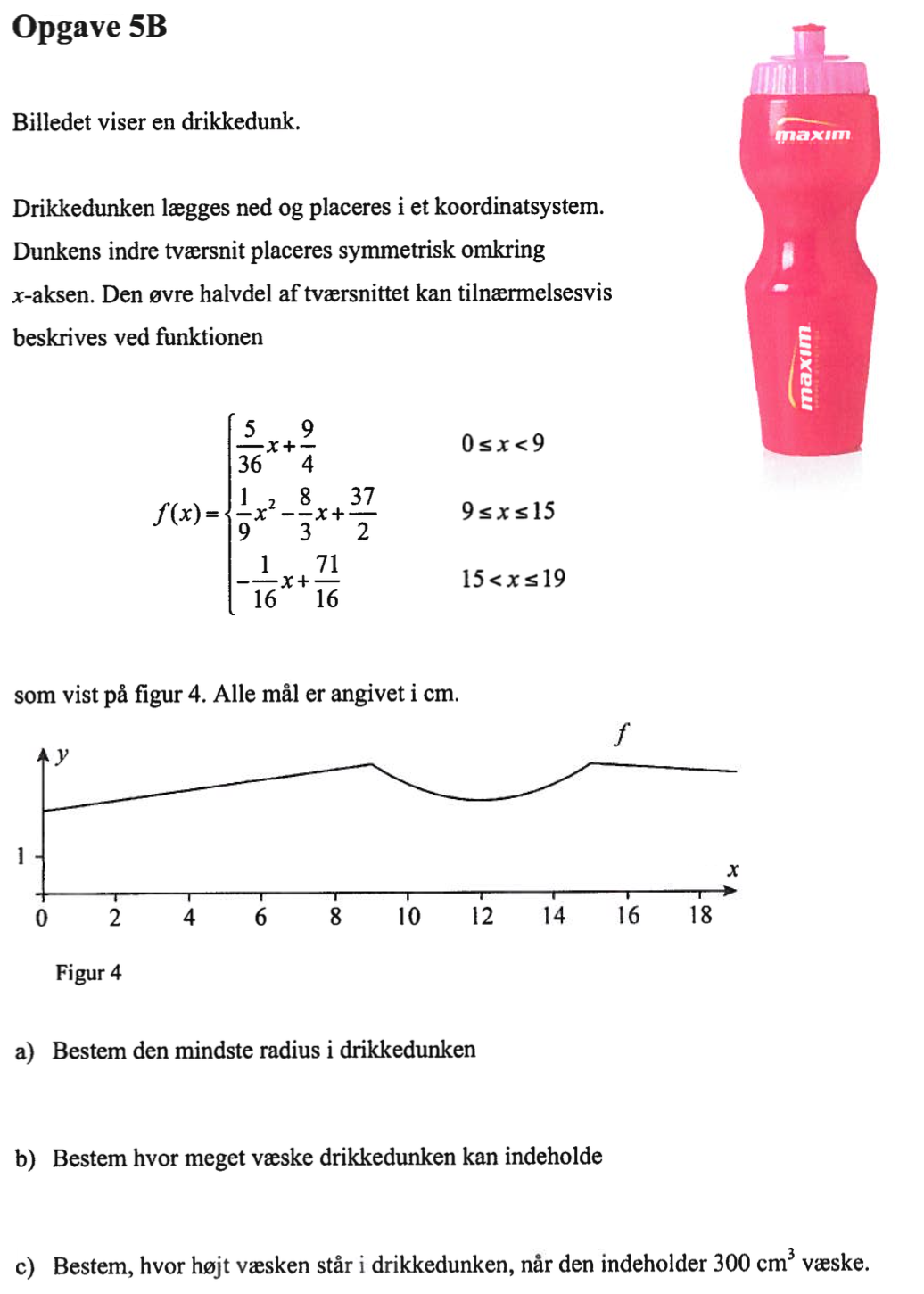
Svar på opgave 5b:
-
Man opretter f(x) i Ti-Nspire som en stykvis funktion:
f(x):=piecewise((5/36)*x+(9/4),0≤x≤9,(1/9)*x2-(8/3)*x+(37/2),9≤x≤15,(−1/16)*x+(71/16),15≤x≤19) ▸ Udført
Mandste radius er lig med mindste værdi af f(x) i definitionsintervallet. Man finder det x der giver mindsteværdien ved hjælp af fMin-kommandoen i Ti-Nspire:
fMin(f(x),x) ▸ x=0
Dvs. mindste radius er f(0) = (5/36)·0 + 9/4 = 9/4 = 2,25
-
Man skal beregne rumfanget af omdrejningslegemet, der fremkommer, når f drejes 360° om x-aksen.
π*integral((f(x))2,x,0,19) ▸ 533.586
Dvs. flaskens rumfang er 533,6 cm3.
-
Man skal beregne den øvre grænse, b, i ovenstående rumfangsformel, der giver rumfanget 300.
solve(π*integral((f(x))2,x,0,b)=300,b) ▸ b=11.303
Dvs. væskens højde er 11,3 cm.

Svar på opgave 5c:
-
Nedenstående billede viser forklaringen indsat.

-
Arealet er 2·x·f(x) = 18·x - 2·x3
-
Man ved fra spørgsmål (a), at nulpunkterne for f er x = -3 eller x = 3. Dvs. man skal søge maksimum af A(x) for -3≤x≤3. Det gøres i Ti-Nspire ved først at finde det x, hvor maksimum antages:
fMax(18*x-2.*x3,x)|−3<x<3 ▸ x=1.73205
Denne x-værdi indsættes i forskriften for arealfunktionen:
18*x-2.*x3|x=1.73205 ▸ 20.7846
Dvs. det største areal er 20,8 .