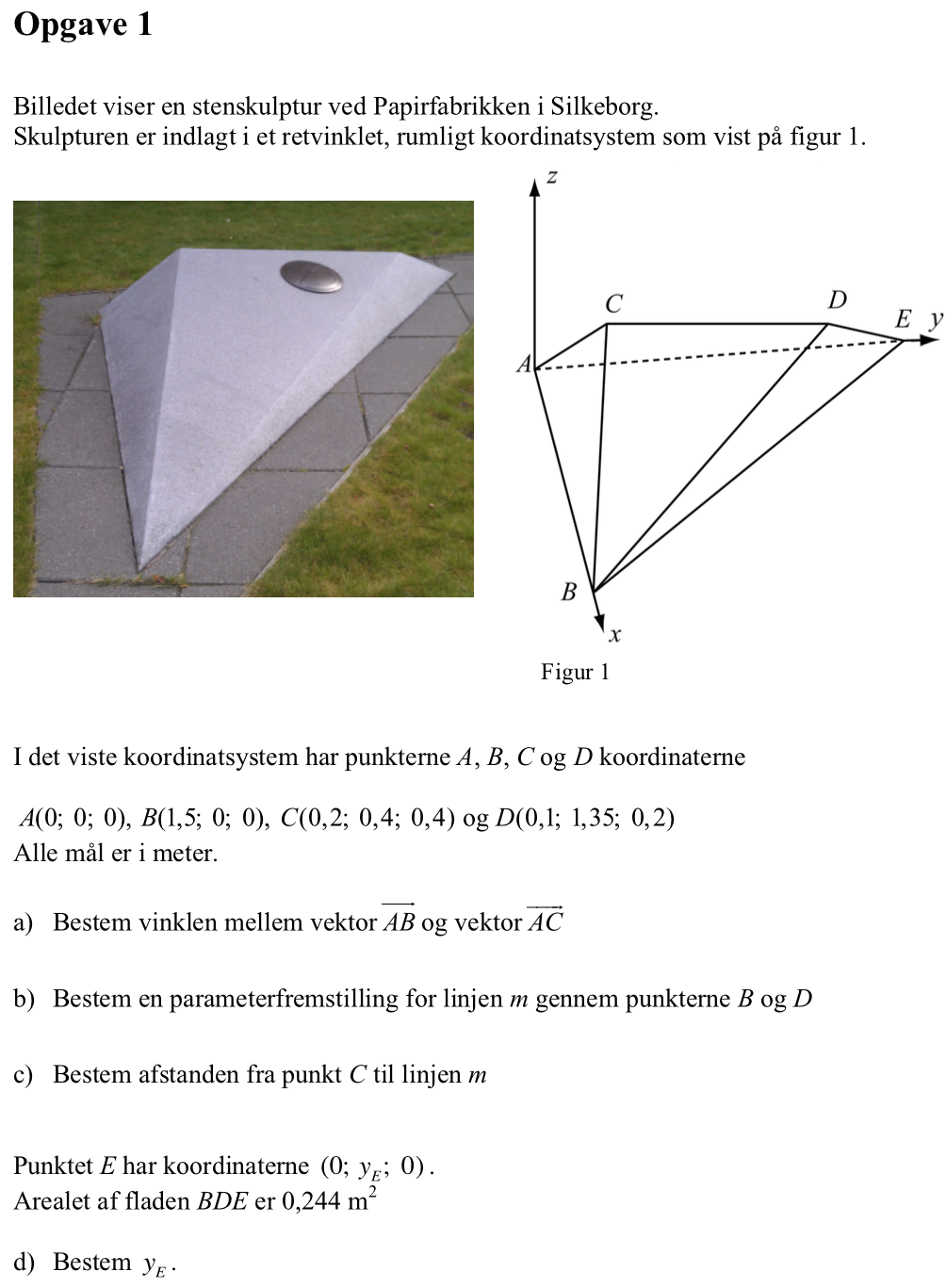
Svar på opgave 1:

1. Man opretter punkterne A-D som stedvektorer:

   a:=[0,0,0] ▸ [0,0,0]

   b:=[1.5,0,0] ▸ [1.5,0,0]

   c:=[0.2,0.4,0.4] ▸ [0.2,0.4,0.4]

   d:=[0.1,1.35,0.2] ▸ [0.1,1.35,0.2]

   Vektorerne AB og AC oprettes:

   ab:=b-a ▸ [1.5,0,0]

   ac:=c-a ▸ [0.2,0.4,0.4]

   Vinklen mellem vektor AB og AC beregnes:

   solve(cos(x*1.°)=dotP(ab,ac)/(norm(ab)*norm(ac)),x)|0<x<180 ▸ x=70.5288

   Dvs. vinklen mellem vektorerne er 70,5°

2. Linjen m skal gå igennem punktet B og have vektoren BD som retningsvektor:

   bd:=d-b ▸ [−1.4,1.35,0.2]

   m(t):=b+t*bd ▸ Udført

   m(t) ▸ [1.5-1.4*t,1.35*t,0.2*t]

   Det giver parameterfremstillingen: m = (1,5;0;0) + t·(-1,4;1,35;0,2), hvor t er et reelt tal

3. Man finder det punkt X på m, hvorom det gælder, at vektor BX er en egentlig vektor og BX står vinkelret på vektor XC. t-værdien for X på linjen m findes ved hjælp af følgende ligning:

   solve(dotP(b-m(t),m(t)-c)=0,t) ▸ t=0 or t=0.638326

   Her er t = 0 en ugyldig løsning, da den giver BX = 0. Den gyldige værdi t = 0,6383 indsættes i m(t), og man bestemmer længden af vektoren XC:

   norm(m(0.638326)-c) ▸ 0.67267

   Dvs. afstanden fra m til C er 0,673 meter

4. Man opretter punktet E = (0,y,0) og vektoren BE

   e:=[0,y,0] ▸ [0,y,0]

   be:=e-b ▸ [−1.5,y,0]

   Arealet af trekant BDE er halvdelen af længden (normen) af krydsproduktet af vektorerne BD og BE. Den y-værdi til E som giver arealet 0,244 findes ved ligningen:

   solve(0.5*norm(crossP(bd,be))=0.244,y) ▸ y=1.23566 or y=1.59934

   Efter billedet at dømme skal y_E være større end y-koordinaten for D, som er 1,35. Dvs. y_E = 1,60

Svar på opgave 2:

1. Man opretter N(t) med konstanterne a og b i Ti-Nspire:

   Man løser ligningerne b·a³ = 27 og b·a²⁸ = 4039 med hensyn til a og b:

   solve(b*a³=27 and b*a²⁸=4039.,a,b) ▸ a=1.22179 and b=14.8038

   Dvs. N(t) = 14,80·1,222^t

2. Man opretter en liste med antal år efter 1962 i Ti-Nspire:

   liste_år:={1965,1986,1987,1988,1990}-1962 ▸ {3,24,25,26,28}

   Tilsvarende opretter man en liste med antal moskusokser

   liste_antal:={27,1715,1968,2383,4039} ▸ {27,1715,1968,2383,4039}

   Derudover opretter man funktionen N(x) = 14,80·1,222^x, som skal bruges til at tegne grafen i Ti-Nspire.

   Man får nedenstående grafer. Den røde kurve er N(t), mens de blå punkter er de sammenhørende værdier af antal år og antal moskusokser.

   

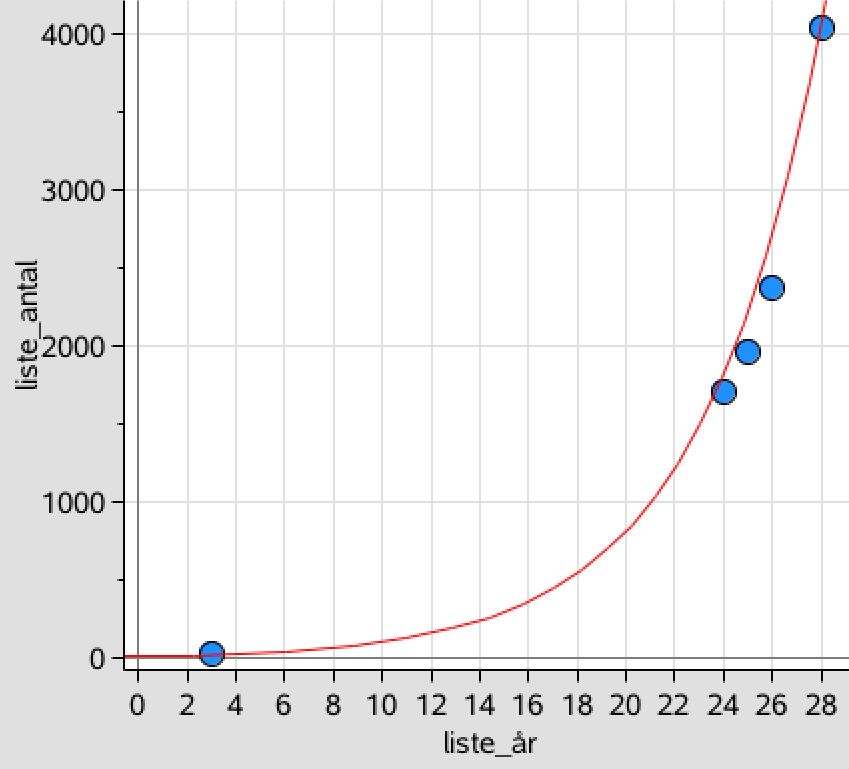
3. Man skal vise at N'(t) er proportional med N(t). Man får:

   N'(t) = 2,966·1,222^t

   N(t) = 14,80·1,222^t

   De to forskrifter ses at være proportionale, da de kun afviger på det konstante led foran potensen.

   Dermed er N en løsning til en differentialligning af formen dN/dt = k·N.

4. Man skal finde N'(1990-1962) = N'(28). Det gøres i Ti-Nspire:

   derivative(n(t),t)|t=1990-1962 ▸ 809.086

   Dvs. væksten i antallet af moskusokser i 1990 er 809 om året

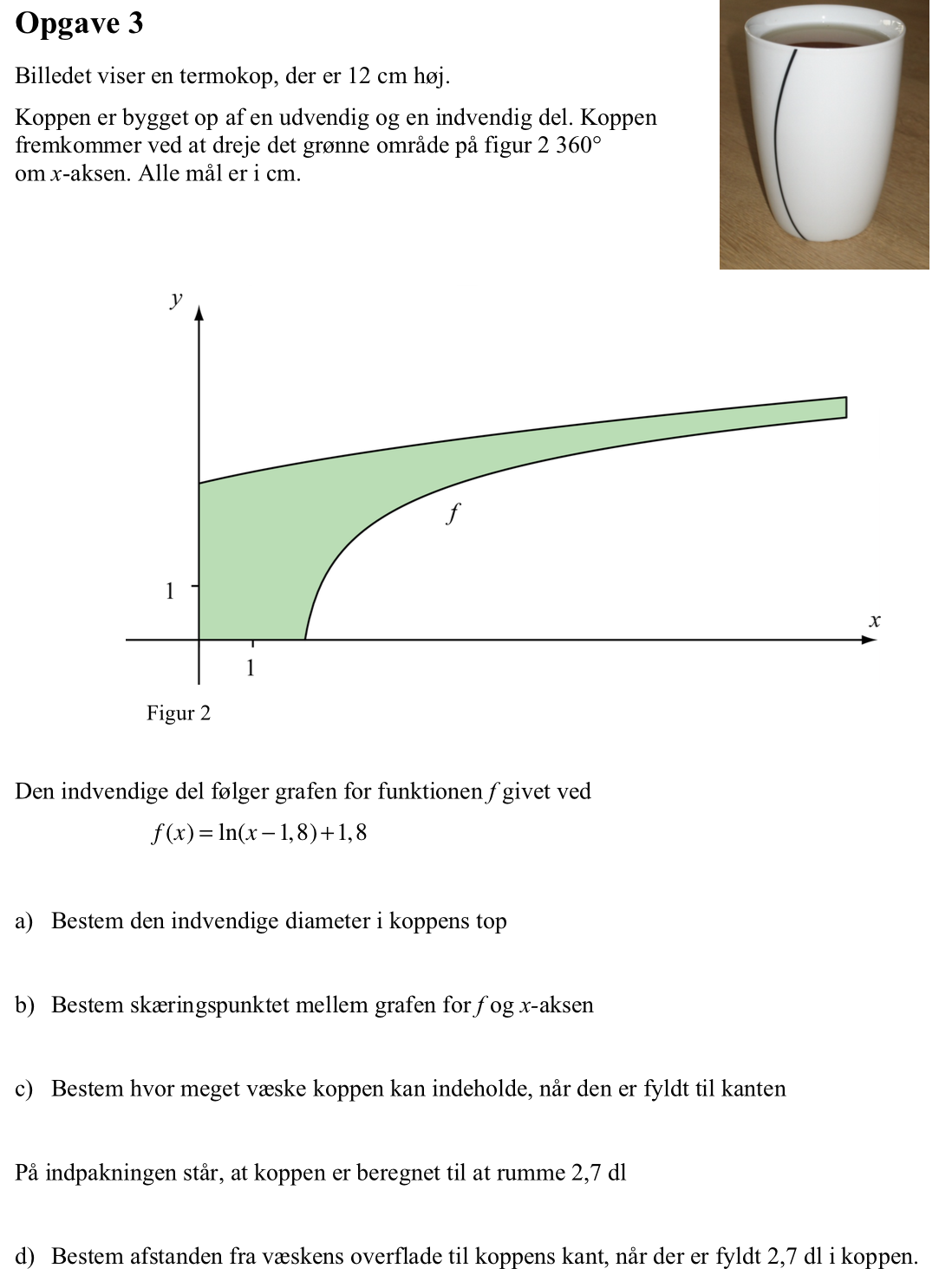
Svar på opgave 3:

1. Man opretter f(x) i Ti-Nspire:

   f(x):=ln(x-1.8)+1.8 ▸ Udført

   Den indvendige diameter i koppens top er 2 gange f(12):

   2·f(12) ▸ 8.24478

   Dvs. diameteren er 8,24 cm

2. Skæringspunktet mellem f og x-aksen findes af ligningen f(x) = 0, der løses med hensyn til x.

   solve(f(x)=0,x) ▸ x=1.9653

   Dvs. (x-værdien af) skæringspunktet er 1,97

3. Man beregner koppens rumfang i Ti-Nspire ved hjælp af volumenformlen for et omdrejningslegeme, der roteres 360° om x-aksen.

   π*integral((f(x))²,x,1.9653,12) ▸ 343.415

   Dvs. koppens indvendige volumen er 343,4 cm³

4. Man indsætter b som øvre grænse i formlen for volumenet og beregner det b, som giver volumenet 2,7 dL = 2,7·0,1L·1000 cm³/L = 270 cm³.

   solve(π*integral((f(x))²,x,1.9653,b)=270,b) ▸ b=10.5748

   Dvs. afstanden for væskens overflade til kantens top er 12 cm - 10,57 cm = 1,43 cm

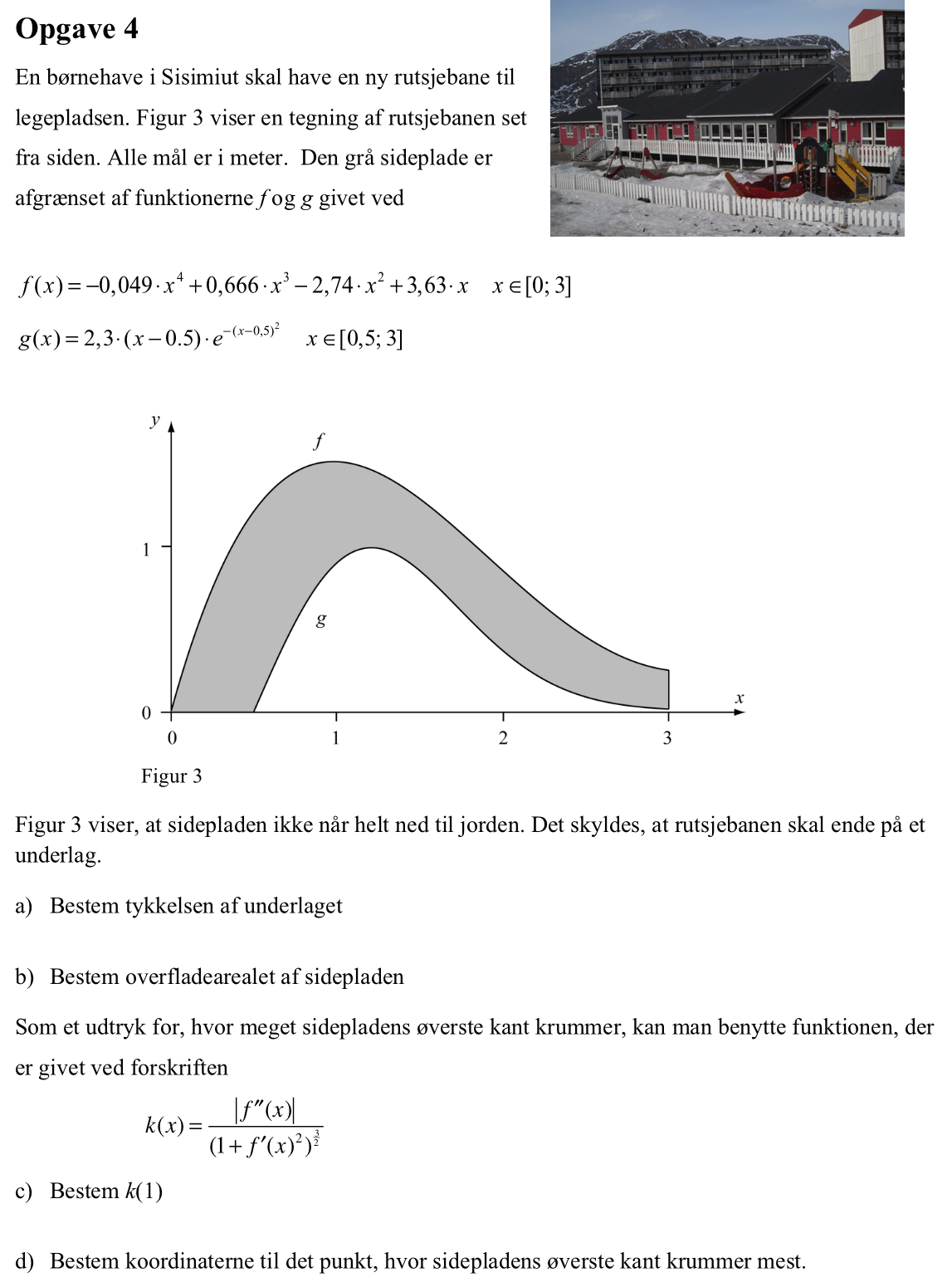
Svar på opgave 4:

1. Man opretter f(x) og g(x) i Ti-Nspire:

   f(x):=−0.049*x⁴+0.666*x³-2.74*x²+3.63*x ▸ Udført

   g(x):=2.3*(x-0.5)*exp(−(x-0.5)²) ▸ Udført

   tykkelsen af underlaget er g(3):

   g(3) ▸ 0.0111

   Dvs. tykkelsen af underlaget er 0,011 m

2. Overfladearealet er integralet af f fra x = 0 til x = 0,5 plus integralet af f - g fra x = 0,5 og x = 3. Dette giver i Ti-Nspire:

   integral(f(x),x,0,0.5)+integral(f(x)-g(x),x,0.5,3) ▸ 1.63232

   Dvs. arealet af sidepladen er 1,63 m²

3. k(x) oprettes i Ti-Nspire.

   k(x):=abs(derivative(f(x),x,2))/(1+(derivative(f(x),x))²)^3/2) ▸ Udført

   Dernæst beregnes k(1):

   k(1) ▸ 2.06486

   Dvs. k(1) = 2,065

4. Den x-værdi, der giver den maksimale krumning, findes i Ti-Nspire ved hjælp af fMax-kommandoen:

   fMax(k(x),x)|0<x<3 ▸ x=0.897061

   Denne x-værdi indsættes i f(x) for at finde y-værdien til punktet:

   f(0.897061) ▸ 1.50044

   Dvs. den maksimale krumning er i punktet (0,897;1,500)

Svar på opgave 5a:

1. Man starter med at finde længden af diagonalen d som vist på nedenstående tegning.

   

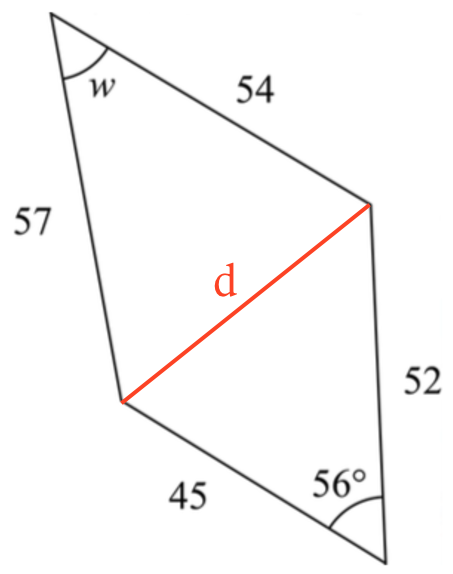
   Dette gøres ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(56.°)=(45²+52²-d²)/(2*45*52),d)|d>0 ▸ d=45.9563

   Værdien af d anvendes derefter til at finde w i en ny cosinusrelation:

   solve(cos(w*1.°)=(54²+57²-45.956²)/(2*54*57),w)|0<w<180 ▸ w=48.8228

   Dvs. w = 48,8°

2. Det fremgår af billedet i opgaven at:

   u = 180° - 158° = 22°.

   Af oplysningen u + v = 50° fås: v = 50° - 22° = 28°

   Dvs. u = 22° og v = 28°

3. Der gælder følgende to ligninger for vektorsummen F1 = F2 + F3: |F₂|·cos(22.°) + |F₃|·cos(28°) = 265 og |F₂|·sin(22.°) = |F₃|·sin(28°). Dette løses med hensyn til |F₂| og |F₃| i Ti-Nspire:

   solve(f2*cos(22.°)+f3*cos(28°)=265 and f2*sin(22.°)=f3*sin(28°),f2,f3) ▸ f2=162.406 and f3=129.589

   Dvs. |F₂| = 162 N og |F₃| = 130 N

Svar på opgave 5b:

1. Man opretter x(t), y(t) og r(t) i Ti-Nspire:

   x(t):=0.5*cos(t)+0.5*sin(0.5*t) ▸ Udført

   y(t):=0.5*sin(t)+0.5 ▸ Udført

   r(t):=[[x(t)][y(t)]] ▸ Udført

   Man får følgende figur i Ti-Nspire:

   

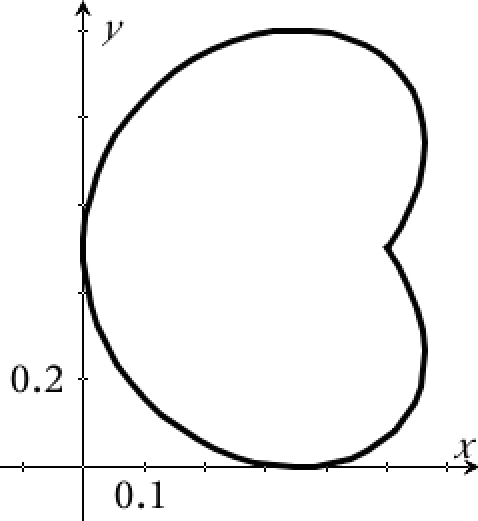
   Nedenfor er vist indtastningsfeltet i Ti-NSpire. Bemærk at man går et step længere end 2π = 6,28 for at få en lukket kurve.

   

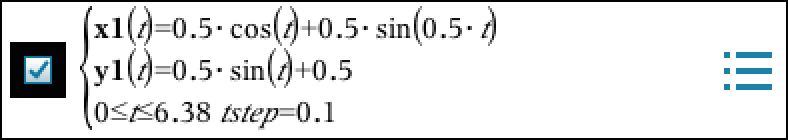
2. Man beregner de x- og y-koordinater, som kurven ligger indenfor ved hjælp af fMin- og fMax-kommandoene i Ti-Nspire:

   fMin(x(t),t)|0<t<2*π ▸ t=3.14159 (minimum for x)

   x(π) ▸ 0.

   fMax(x(t),t)|0<t<2*π ▸ t=0.505361 or t=5.77782 (maksimum for x)

   x(0.505361) ▸ 0.5625

   fMin(y(t),t)|0<t<2*π ▸ t=4.71239 (minimum for y)

   y(4.71239) ▸ 2.6E−13

   fMax(y(t),t)|0<t<2*π ▸ t=1.5708 (maksimum for y)

   y(1.5708) ▸ 1.

   Kassens længde = 1,5708 m - 0 m = 1,5708 m. Kassens bredde = 0,5625 m - 0 m = 0,5625 m.

   Dvs. kassens indvendige dimensioner = Længde x Bredde = 1,57 m x 0,56 m.

3. Man opretter tværvektoren til r(t) (kaldet r_hat(t)) i Ti-Nspire:

   r_hat(t):=[[−y(t)][x(t)]] ▸ Udført

   Arealet af bordpladen beregnes ved hjælp af formlen i TI-Nspire:

   (1/2)*integral(dotP(r_hat(t),derivative(r(t),t)),t,0,2*π) ▸ 0.452065

   Dvs. bordpladens areal er 0,452 m²

Svar på opgave 5c:

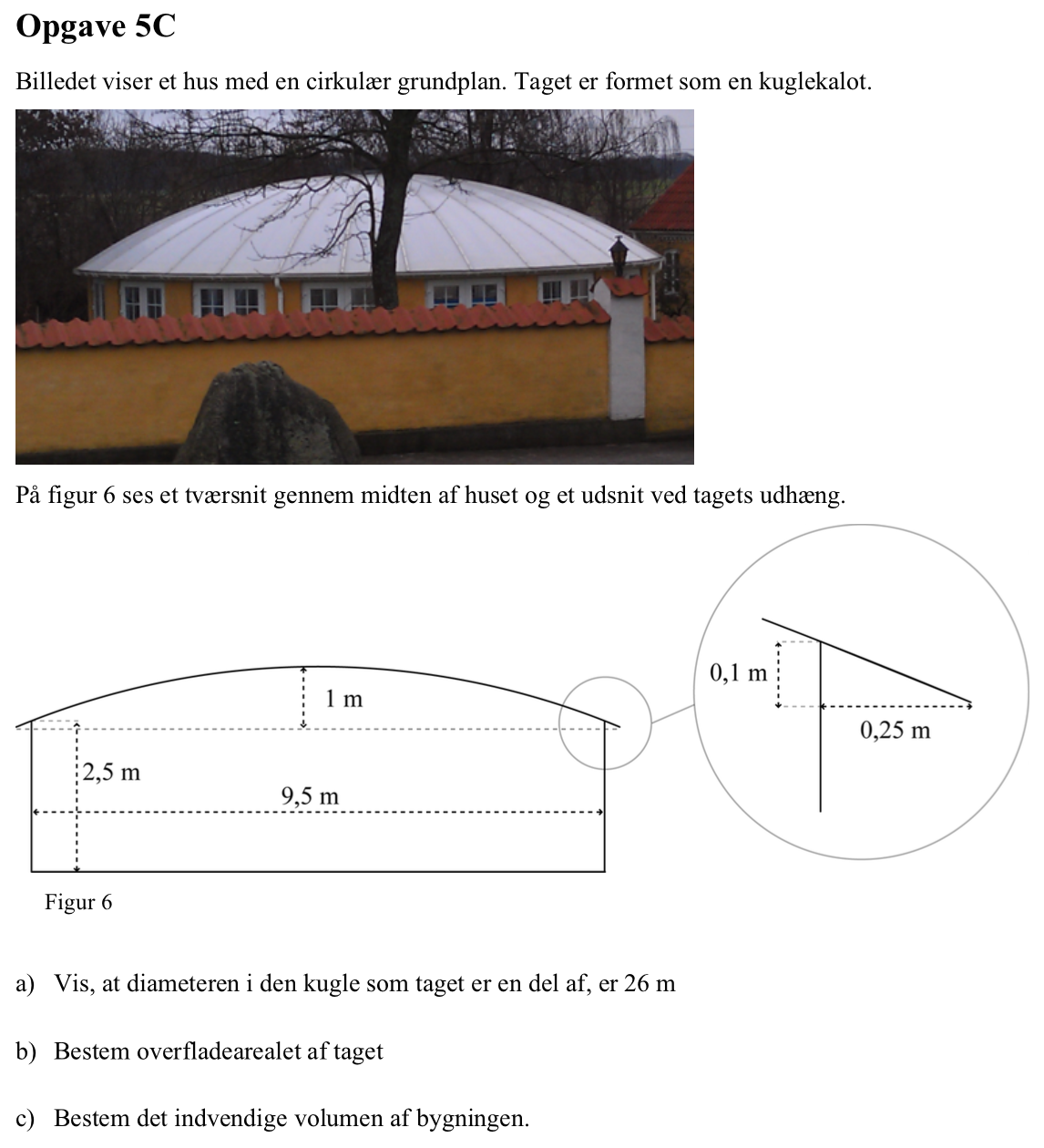
1. Tag-buen mellem væggene er et cirkelafsnit med korden 9,5/2 m og pilhøjden (1 - 0,1) m = 0,9 m. Man kan finde radius ved hjælp af Pythagoras læresætning som vist på nedenstående figur:

   

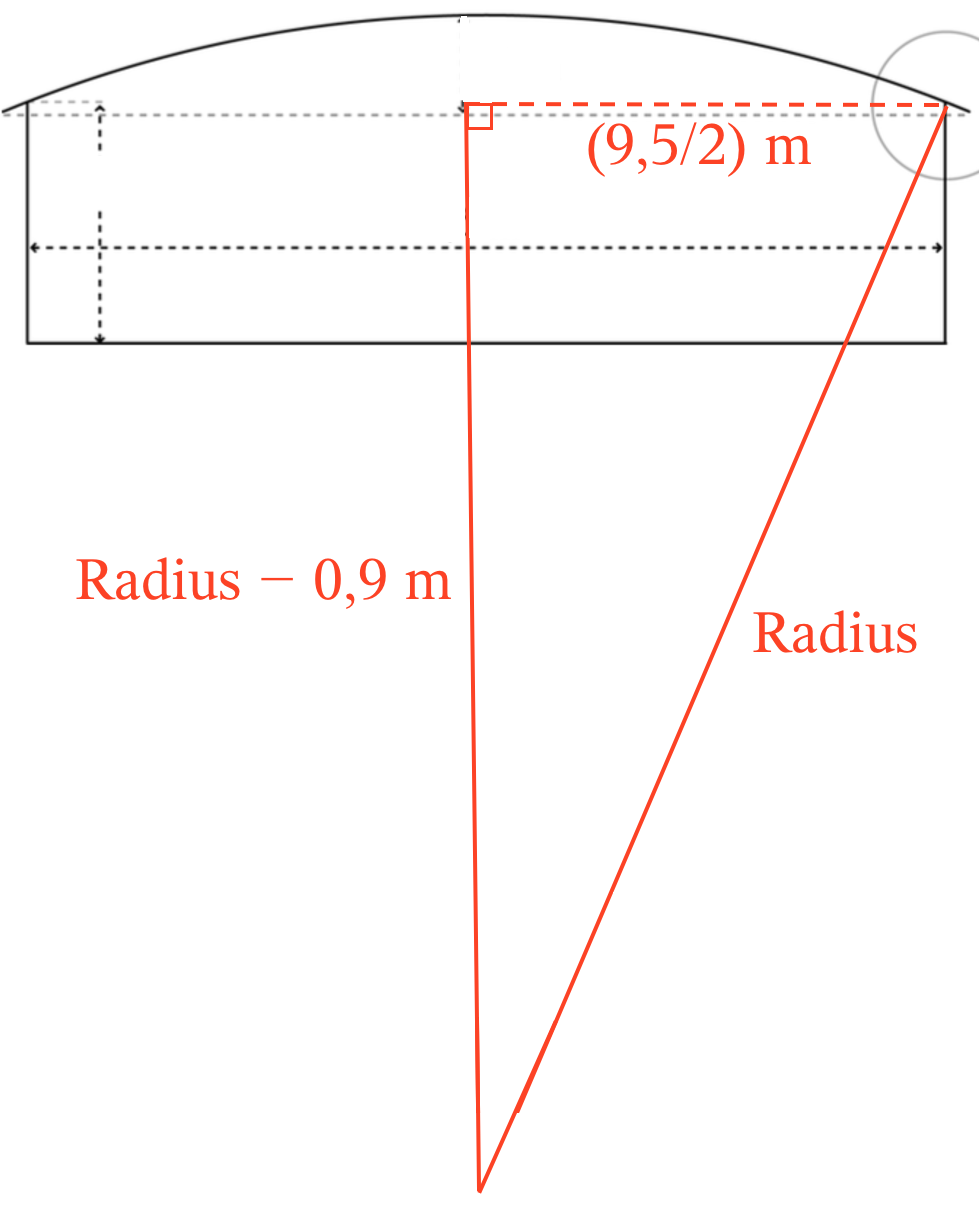
   Radius findes i Ti-Nspire:

   solve(r²=(9.5/2)²+(r-0.9)²,r) ▸ r=12.9847

   Dvs diameteren af kuglen = 2·12,98 m = 26,0 m

2. Arealet findes af formlen overfladearealet af et kugleafsnit: π·h·d, hvor h er pilhøjden og d er kuglens diameter.

   Arealet er dermed: π·(26,0 m)·(1 m) = 81,7 m²

3. Den indvendige volumen af bygningen er volumenet af en kuglekalot plus rumfanget af en cylinder. Man får:

   (π/6)·0,9·(3·(9,5/2)² + 0,9²) + π·(9,5/2)²·2,5 m³ = 209,5 m³.