Svar på opgave 1:
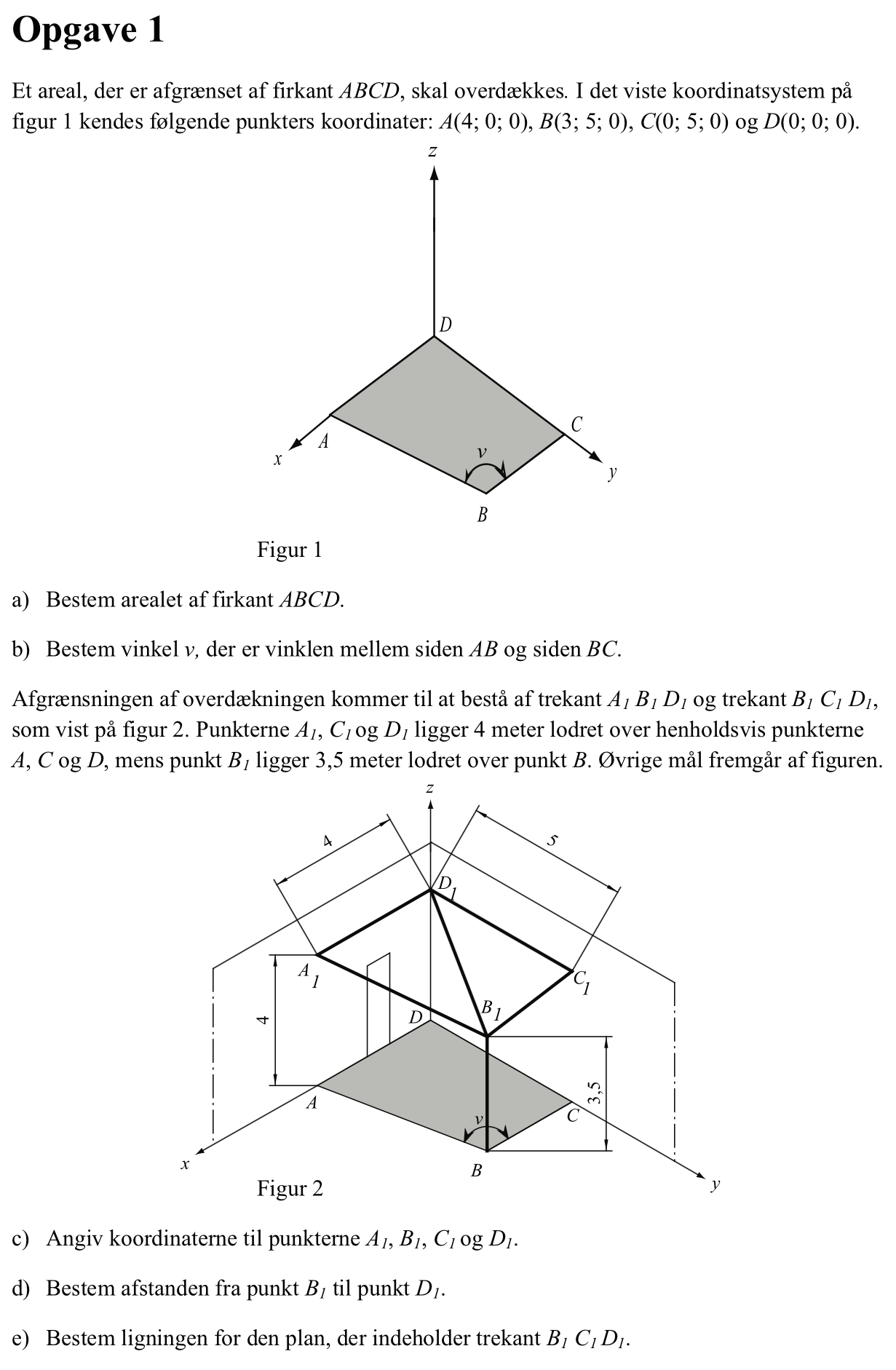
Opgaven løst i Geogebra. De røde bogstaver i værktøjslinjen foroven henviser til underopgaver.
-
Arealet af ABCD findes i Geogebra ved at tegne et polygon efter punkterne ABCD. Dette areal ses at være 17,5
-
Man måler vinklen med vinkelværktøjet ved at klikke A-B-C. Det giver 101,3°
-
A1, B1, C1 og D1 fremkommer af A, B, C og D ved at lægge punktet højde over jorden til z-koordinaten. Man får A1 = (4,0,4), B1 = (3;5;3,5), C1 = (0,5,4) og D1 = (0,0,4)
-
Man bruger afstandsværktøjet og klikker på B1-D1. Afstanden er 5,85
-
Man bruger værktøjet plan-gennem-tre-punkter og klikker på B1-C1-D1. Planens ligning aflæses til 2,5x + 15z = 60 eller ved at dividere igennem med 2,5: x + 6z = 24
Løst i Ti-Nspire:
-
Arealet findes som summen af arealerne af trekanterne ABD og trekant BCD. Man opretter fire vektorer i Ti-NSpire: ab:=[−1,5,0], ad:=[−4,0,0], cb:=[3,0,0] og cd:=[0,−5,0].
Man finder trekanternes arealer som halvdelen af krydsproduktet af ab og ad plus halvdelen af krydsproduktet af cb og cd. Man bruger følgende Ti-Nspire kommando:
(1/2)*norm(crossP(ab,ad))+(1/2)*norm(crossP(cb,cd)) ▸ 35/2
(crossP() er beregner krydsproduktet af to vektorer og norm beregner længden af en vektor.)
Dvs. arealet af ABCD er 35/2 = 17,5
-
Man bruger formlen for vinklen mellem to vektorer, her er det vektorerne BA (= -AB) og BC. Man bruger følgende kommando:
solve(cos(x*1.°)=dotP(−ab,bc)/(norm(−ab)*norm(bc)),x)|0<x<180 ▸ x=101.31
Dette giver vinklen v = 101,3°
-
Som ovenfor.
-
Man bruger afstandsformlen for to punkter i rummet. Det giver: Afstand mellem B1 og D1 = √[(0-3)2 + (0-5)2 + (4-3,5)2] = √[9 + 25 + 0,25] = 5,852
-
Man finder planens ligning ved at benytte at skalarproduktet mellem normalvektoren til planen (n) og en vilkårlig vektor i planen er 0. Som vilkårlig vektor i planen oprettes vektoren C1P, hvor P = (x,y,z). Det giver følgende i Ti-Nspire:
n:=crossP(c1b1,c1d1) ▸ [−2.5,0.,−15] (normalvektoren oprettes som krydsproduktet af C1B1 og C1D1)
p:=[x,y,z] ▸ [x,y,z] (opret tilfældigt punkt i rummet med koordinaterne (x,y,z))
c1p:=p-c1 ▸ [x,y-5,z-4] (opret tilfældig vektor C1P i planen)
dotP(n,c1p)=0 ▸ −2.5*x-15*(z-4)=0 (sæt skalarproduktet af n og C1P lig med 0)
Dvs. planens ligning er −2,5·x - 15·(z-4) = 0 eller x + 6z - 24 = 0

Svar på opgave 2:
-
Nedenstående tegning er lavet i Geogebra. Den viser placeringen af cirklens centrum, C.
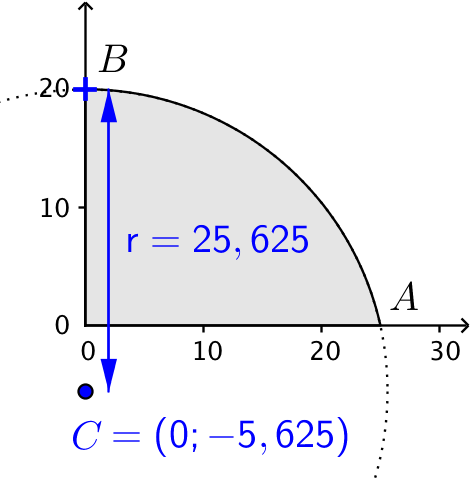
På grundlag af denne tegning finder man cirklens ligning til: (x - 0)2 + (y + 5,625)2 = 25,6252 eller x2 + (y + 5,625)2 = 656,641
-
Rumfanget kan beregnes som rumfanget af et omdrejningslegeme, men også som rumfanget af en kuglekalot.
For at beregne beregnes først x-koordinaten til punktet A, dvs. cirklens skæring med x-aksen.
A findes ved at sætte y = 0 i cirklens ligning og vælge den positive. Man får :
x2 + (0 + 5,625)2 = 656,641 ⇒
x2 = 656,641 - 5,6252 ⇒
x2 = 625 ⇒
x = 25, dvs. cirklen skærer x-aksen i x = 25
Dernæst oprettes en funktion f(x), der er cirklens ligning omskrevet, så man har y som funktion af x:
x2 + (y + 5,625)2 = 656,641 ⇒
(y + 5,625)2 = 656,641 - x2 ⇒
y + 5,625 = √[656,641 - x2] ⇒
y = √[656,641 - x2] - 5,625
Dvs. man opretter følgende funktion på intervallet 0 < x < 25:
f(x):=√(656.641-x2)-5.625 ▸ Udført
Man bruger nu formlen for rumfanget af omdrejningslegemet af en kurve der roteres 360° omkring y-aksen:
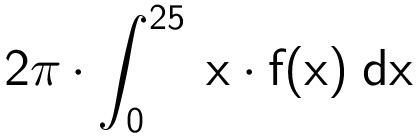
Dette giver i Ti-Nspire:
2*π*Integral(x*f(x),x,0,25) ▸ 23823.7.
Formlen for rumfanget af en kuglekalot giver tilsvarende: (π/6)*20*(3*25.2+202) ▸ 23823.7.
Dvs. rumfanget af underdelen er = 23824 cm3
-
For at finde yT opretter man en funktion, g(y), der er ciklens ligning omskrevet, så man har x som funktion af y (efter samme metode som i opgave b):
g(y):=sqrt((25.625)2-(y+5.625)2) ▸ Udført
Man skal finde det yT, hvor integralet langs y-aksen fra 0 til yT giver halvdelen af arealet af det grå område. Dvs. man skal løse ligningen:
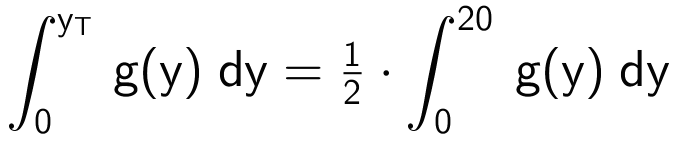
Man bruger følgende Ti-Nspire kommando:
solve(Integral(g(y),y,0,yt)=(1/2)*Integral(g(y),y,0,20),yt) ▸ yt=7.8822
Dvs. yT = 7,88 cm
-
Man finder rumfanget af den nye underdel ved at bruge formlen for rumfanget af et omdrejningslegeme omkring y-aksen:
2.*π*Integral(x*20*cos((π/50)*x),x,0,25) ▸ 18169
Rumfanget af den nye underdel er dermed: 18.169 cm3
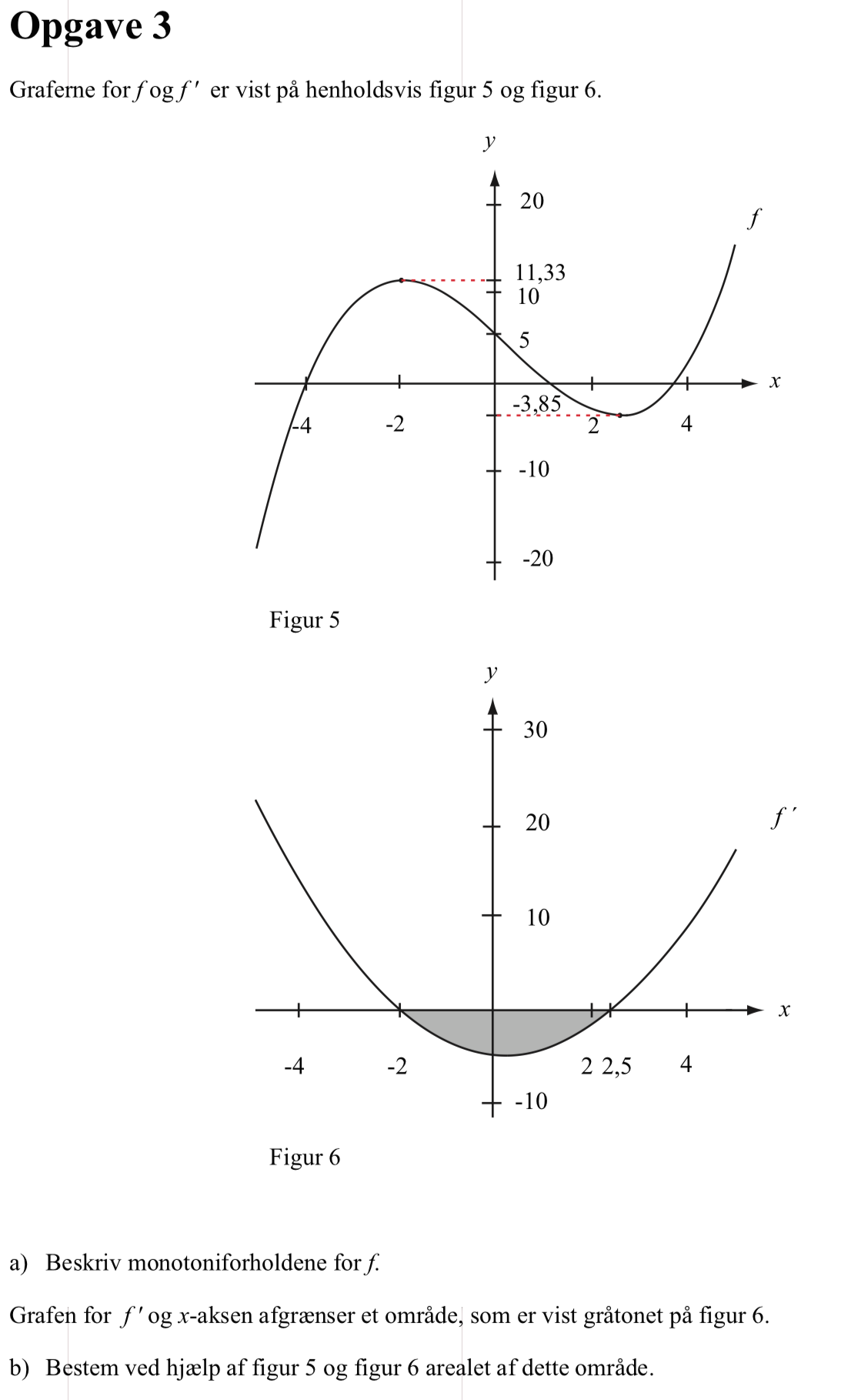
Svar på opgave 3:
-
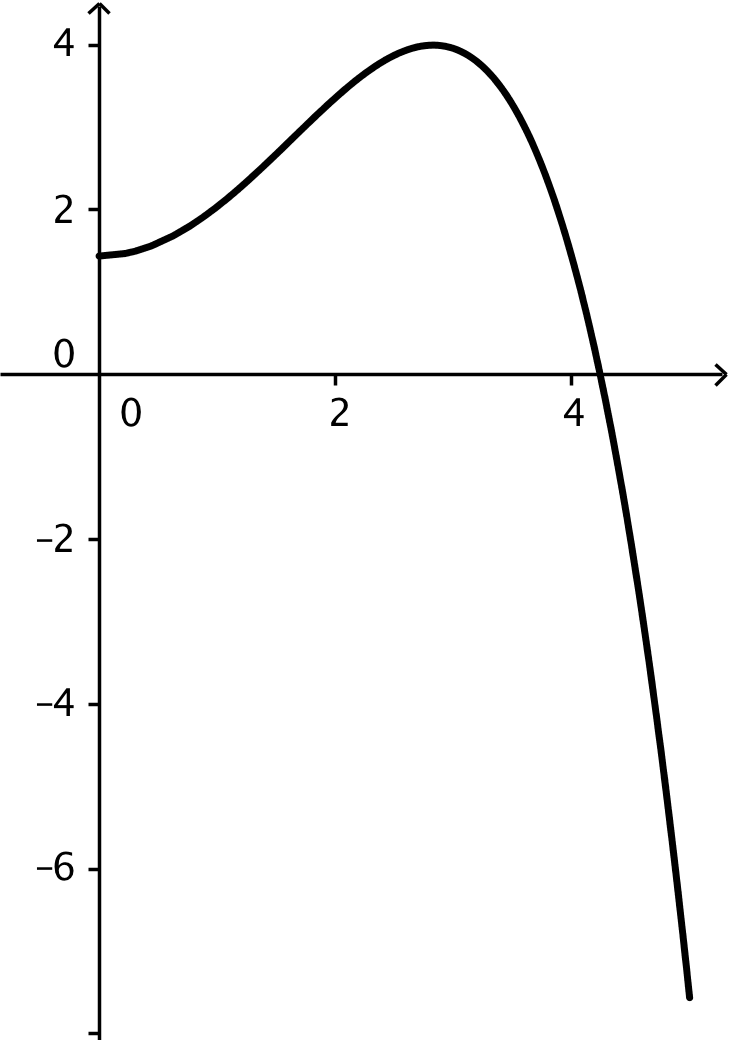
Monotoniforholdene for f fremgår af grafen for f´.
Da f´ > 0 for x < -2 ∨ x > 2,5 og da f´ < 0 for -2 < x < 2,5
...gælder, at...
f er voksende for x < -2 ∨ x > 2,5 og f er aftagende for -2 < x < 2,5
-
Arealet af området under kurven er
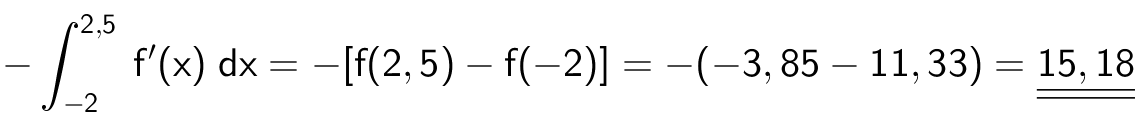
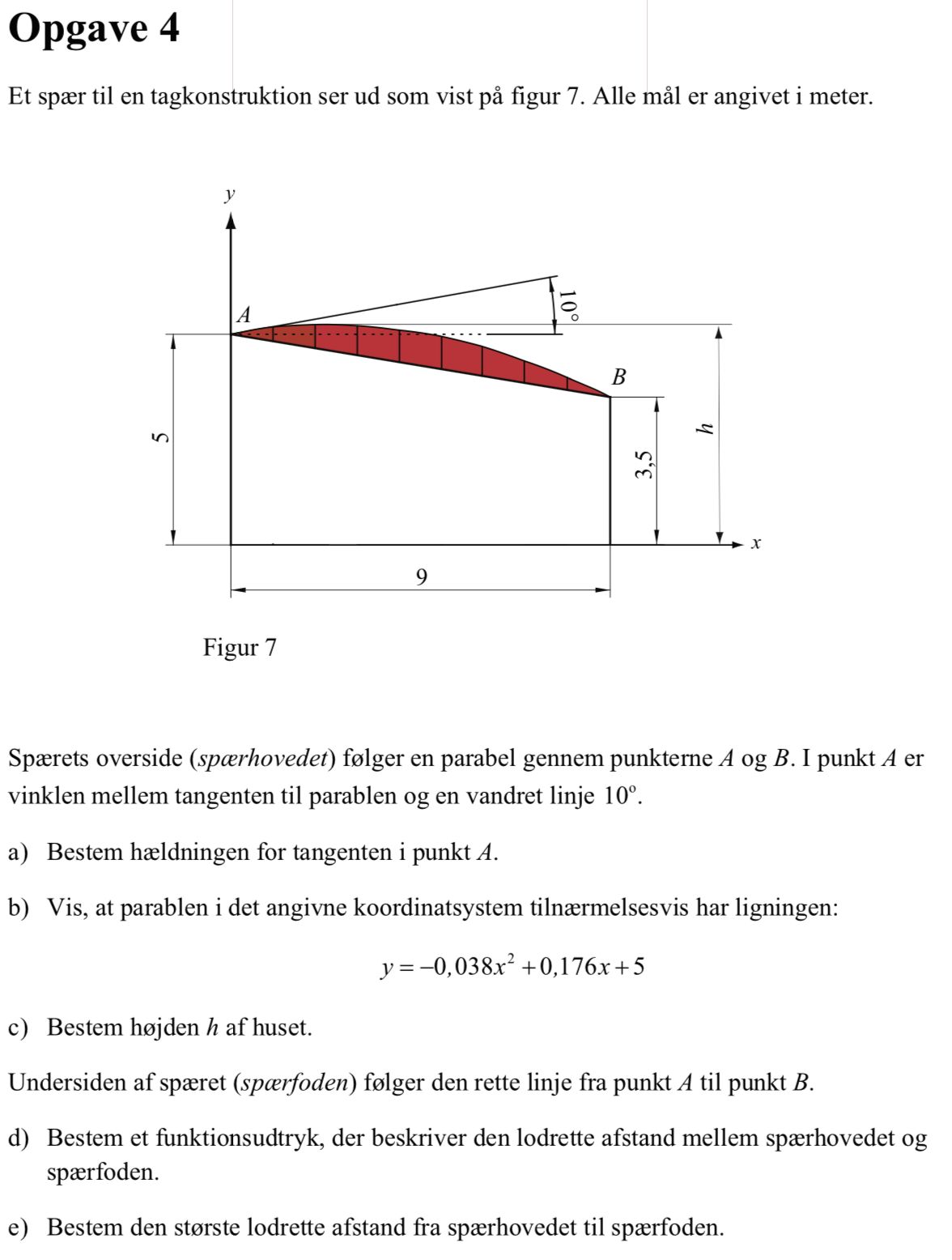
Svar på opgave 4:
-
Der gælder, at hældning = tan(10°) ⇒ hældning = 0,1763
-
Ligningen har formen y = ax2 + bx + c, som er ligningen for en parabel eller forskriften for et andengradspolynomium.
For parabel-ligningen gælder, at c er skæringen med y-aksen og b er hældningen i skæringen med y aksen. Det giver her, at c = 5 og b = 0,1763, som man fandt i delopgave a).
Man har nu y = ax2 + 0,1763x + 5. Koefficienten a kan bestemmes ud fra et punkt, hvor x er forskelligt fra 0, blev brugt til at finde b og c. Man bruger punktet B = (9;3,5).
Man indsætter x = 9 og y = 3,5 i ligningen y = ax2 + 0,1763x + 5 og får:
3,5 = a·92 + 0,1763·9 + 5 ⇒ a·92 = -0,1763·9 - 5 + 3,5 ⇒ a = (-0,1763·9 - 5 + 3,5)/·92 ⇒ a = −0.0381
Dvs. man får, at parablens ligning er -0,038·x2 + 0,176·x + 5, som man skule vise.
-
For at finde højden bruger man formlen for y-værdien af toppunktet for en parabel:
yT = c - b2/(4a) = 5 - 0,1762/(4·(−0.038)) = 5,2038
Dvs. højden er 5,20 m
-
For at finde afstanden mellem spærhoved og spærfod, skal man finde ligningen for den rette linje gennem A og B og trække denne y-værdi fra parablens ligning.
Linjen gennem A og B kan skrives som y = αx + β. Der er β = 5, som er y-værdien for A, der er det punkt, hvor x = 0.
Det giver y = αx + 5. Man indsætter derefter punktet B = (9;3,5) for at finde α: 3,5 = α9 + 5 ⇒ α = (3,5 - 5)/9 ⇒ α = −0,167. Det giver ligningen for spærfoden: y = -0,167x + 5. Dette trækkes fra parablens ligning og man får, at afstand =
-0,038·x2 + 0,176·x + 5 - (-0,167x + 5) = -0,038·x2 + 0,3427·x
-
Afstandsformlen er også et andengradspolynomium. Man bruger igen formlen for y-værdien af toppunktet for en parabel:
Her er a = -0,038, b = 0,3427 og c = 0. Man får den største afstand er:
-0,34272/(4·(−0,038)) meter = 0,77 meter

Svar på opgave 5:
-
Banekurve tegnet i Geogebra.
-
Banekurven skærer x-aksen når y(t) = 0, dvs. når -0,04·t2 + 0,8·t = 0 (2 < t ≤ 27) ⇒ t = 20.
Det giver: skæringspunkt med x-aksen = r(10) = (√(20 - 2),0) = (4,243;0)
-
Man skal finde det punkt hvor y'(t) = 0. y'(t) = -0,08·t + 0,8. Man finder det t der gør at dette er lig med 0: -0,08·t + 0,8 = 0 ⇒ t = -0,8/(-0,08) ⇒ t = 10.
Det punkt, der har vandret tangent (vandret hastighedsvektor) er derfor: r(10) = (√(10 - 2), -0,04·102 + 0,8·10) = (2,828;4)
-
Man skal finde det punkt hvor skalarproduktet af stedvektoren r(t) og hastighedsvektoren v(t) er 0.
v(t) = (x'(t),y'(t)) = (1/(2·√(t - 2)),(-0,08·t + 0,8)).
Man får: r(t)·v(t) = 0 ⇒ x(t)·x'(t) + y(t)·y'(t) = 0 ⇒ [√(t - 2)]/[2·√(t - 2)] + [-0,04·t2 + 0,8·t]·[-0,08·t + 0,8] = 0 ⇒ 0,5 + 0,0032·t·(t-20)·(t-1) = 0. Dette løses i CAS:
solve(0.5+0.0032*t*(t-20)*(t-1)=0,t) ▸ t=−0.70495 or t=11.6037 or t=19.1012
Af disse t-værdier er t = 11,6 og t = 19,1 gyldige.
Det er dermed de t-værdier, hvor stedvektoren r(t) står vinkelret på hastighedsvektoren v(t).
(Det bemærkes, at der er to værdier, hvor opgaven kun taler om en.)
Svar på opgave 6:
-
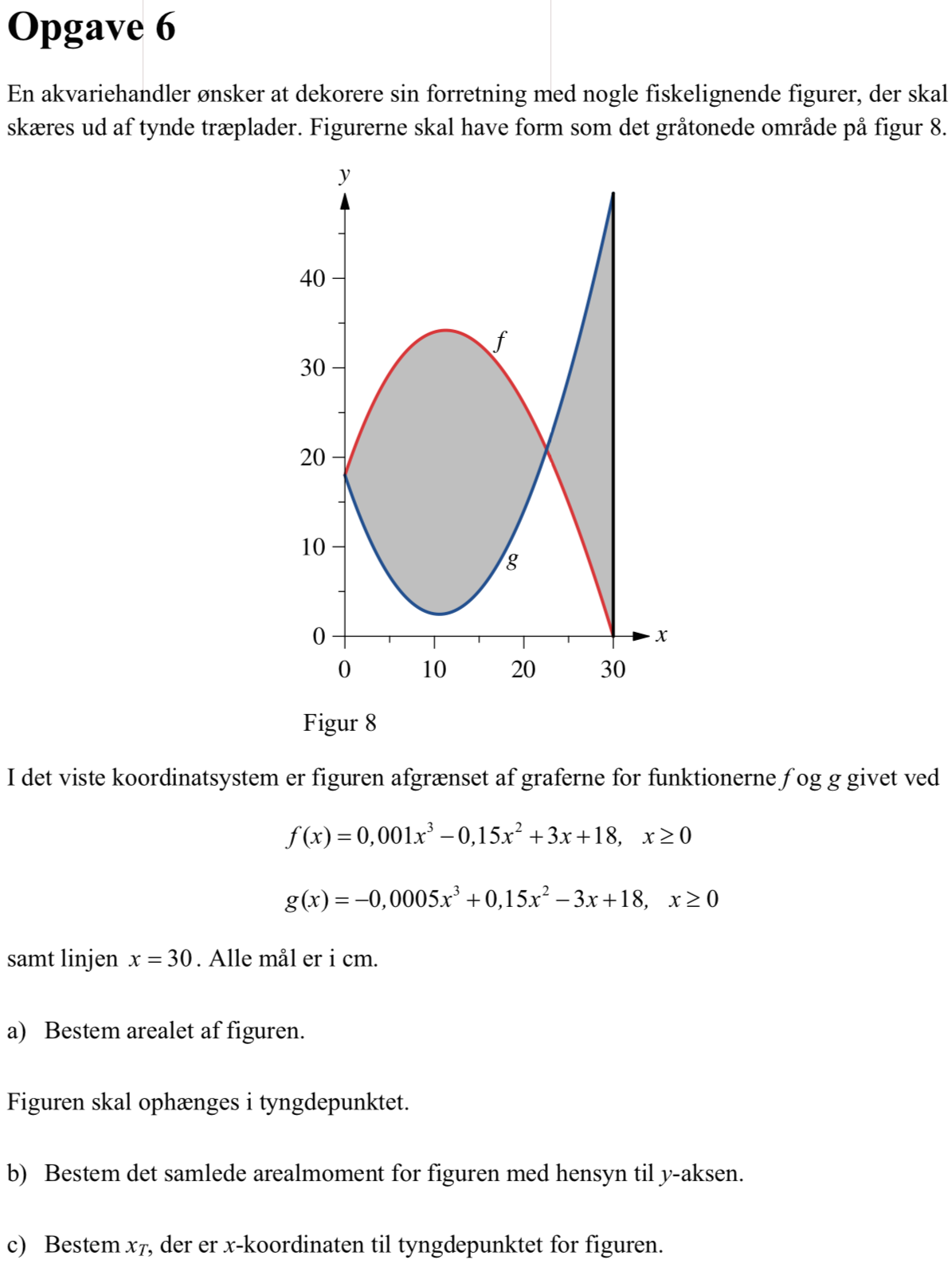
Man opretter funktionerne f(x) og g(x) i Ti-Nspire:
f(x):=0.001*x3-0.15*x^(2)+3*x+18 ▸ Udført
g(x):=−0.0005*x3+0.15*x^(2)-3*x+18 ▸ Udført
Man skal finde skæringspunktet for funktionerne for at kunne beregne arealet mellem dem. Man får:
solve(f(x)=g(x),x) ▸ x=0. or x=22.540 or x=177.46
Det eneste gyldige skæringspunkt er x = 22,54. Man skal integrere f(x) - g(x) fra x = 0 til x = 22,54 og g(x) - f(x) fra x = 22,54 til x = 30. Man får arealet:
Integral(f(x)-g(x),x,0,22.5403)+Integral(g(x)-f(x),x,22.5403,30) ▸ 647.85
Dvs. arealet mellem kurverne er 647,9 cm2
-
Arealmomentet findes ved at gange integranden med x i formlen for arealet:
Integral(x*(f(x)-g(x)),x,0,22.5403)+Integral(x*(g(x)-f(x)),x,22.5403,30) ▸ 10039.2
Dvs. arealmomentet er 10.040 cm3
-
x-koordinaten for tyngdepunktet er arealmomentet divideret med arealet, dvs. xT = 10039.23/647.8503 cm = 15,5 cm