

Svar på opgave 1:
-
Grafen for f tegnet i Excel.
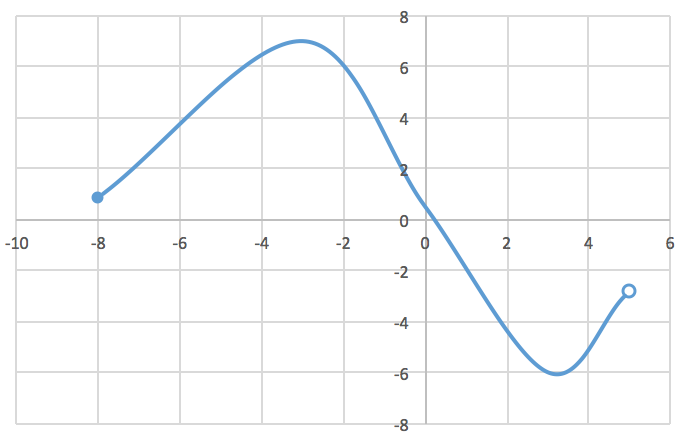
Det bemærkes at hverken minimum- eller maksimum-værdien kan antages i definitionsmængdens højre endepunkt (5), da det ikke er en del af definitionsmængden. Maksimum og minum skal enten antages i venstre endepunkt eller et lokalt ekstremum.

Svar på opgave 2:
-
dy/dx = f´(x) = 6x2 - 2x. y = f(x). Man skal vise at højre og venstre side giver det samme, når man indsætter f(x) og f´(x) i differentialligningen. Man får:
Venstre side: dy/dx + 2y = 6x2 - 2x + 2·(2x3 - x2) = 6x2 - 2x + 4x3 - 2x2 = 4x3 + 4x2 - 2x
Højre side: 4x3 + 4x2 - 2x
Da højre og venstre side i differentialligningen giver det samme med f(x) indsat, er f(x) en løsning til differentialligningen
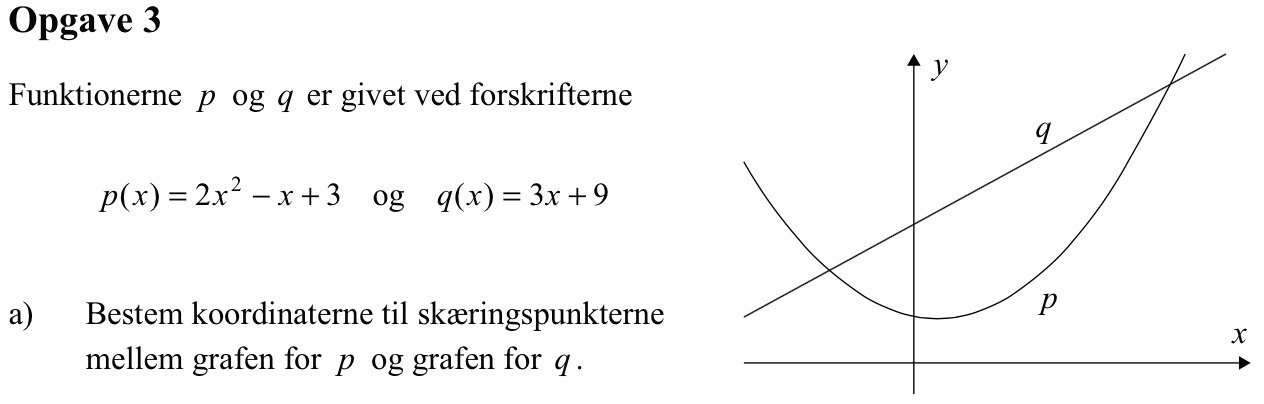
Svar på opgave 3:
-
Man skal løse ligningen p(x) = q(x) med hensyn til x. Man får:
p(x) = q(x) ⇒ 2x2 - x + 3 = 3x + 9 ⇔
2x2 - x + 3 - 3x - 9 = 0 ⇔
2x2 - 4x - 6 = 0 ⇔
x2 - 2x - 3 = 0 ⇔
x = 1 ± 0,5·√[4 + 12] ⇔
x = 1 ± 2 ⇔
x = -1 ∨ x = 3

Svar på opgave 4:
-
En vilkårlig stamfunktion, F(x), til f(x) er givet ved
F(x) = 0,5·x6 - 2x3 + 0,5·x + k, hvor k er en konstant.
Den stanfunktion, der går i gennem P(1,3) skal opfylde ligningen: F(1) = 3 som medfører:
F(1) = 3 ⇒ 0,5·16 - 2·13 + 0,5·1 + k = 3 ⇔ 0,5 - 2 + 0,5 + k = 3 ⇔ k = 4
Dvs. den søgte stamfunkton til f(x) er F(x) = 0,5·x6 - 2·x3 + 0,5·x + 4

Svar på opgave 5:
-
a er givet ved: a = (2100-2400)/(60-50) = -30.
Man har dermed A(x) = -30x + b. Derefter findes b ved at indsætte x = 50, det giver:
A(50) = -30·50 + b = 2100 ⇒ b = 2100 + 1500 = 3900.
Det giver: A(x) = -30x + 3.900
Når x stiger med 5 kr., vil afsætningen falde med 30·5 stk. = 150 stk.


Svar på opgave 6:
-
Man skal isolere a i følgende udtryk:
1 + a/b = a + b ⇒
b + a = ab + b2 ⇒
a - ab = -b + b2 ⇒
a·(1 - b) = -b·(1 - b) ⇒
a = - b (b ≠ 0 og b ≠ 1)
For b = 0 er udtrykket ikke er defineret, og for b = 1, får man 1 + a = a + 1, dvs. a ∈R.
-
2) Man opløfter begge sider i anden potens
3) Man ganger på begge sider med P
4) Man dividerer på begge sider med 2·F·O
5) Man ganger på begge sider med R·(2·F·O)/(P·Q2), hvorved R er isoleret

Svar på opgave 7:
-
Opgaven løst i Excel (se også excel-filen Golf).
I Excel bruges kommandoen "=MIDDEL(B:B)" for at finde middelværdien af tallene i kolonne B, der indehoilder udbudspriser.
Dette giver middelværdien 197.662
Første kvartil af udbudspriserne findes med kommandoen "=KVARTIL(B:B;1)". Det giver 1 kvartil = 142.150
Medianen af udbudspriserne findes med kommandoen "=KVARTIL(B:B;2)". Det giver median = 212.400
3. kvartil af udbudspriserne findes med kommandoen "=KVARTIL(B:B;3)". Det giver 3. kvartil = 249.900
-
Nedenstående graf med tendenslinje er tegnet i Excel.
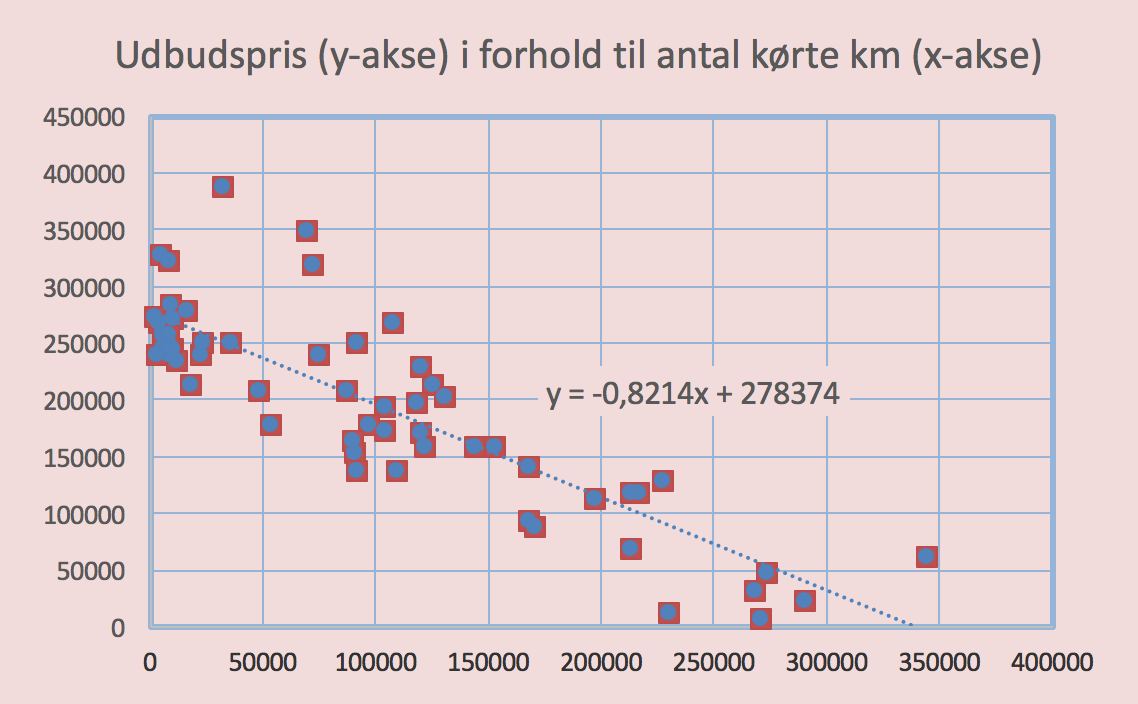
u(x) aflæses af tendenslinjen som -0,821x + 278.374
-
Man vælger "Funktioner - Dataanalyse - Regression" i Excel.
I den øverste del af dialogboksen vælges kolonne A som x-værdier og kolonne B som y-værdier. Desuden vælges 95% konfidensinterval.
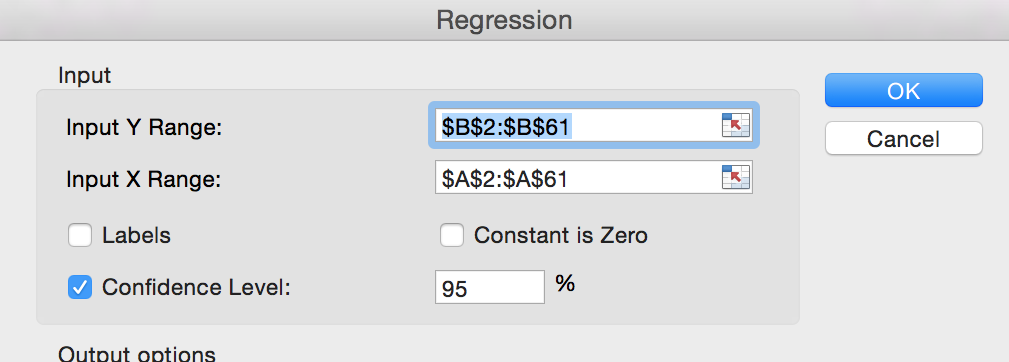
Endelig trykkes OK og man får:
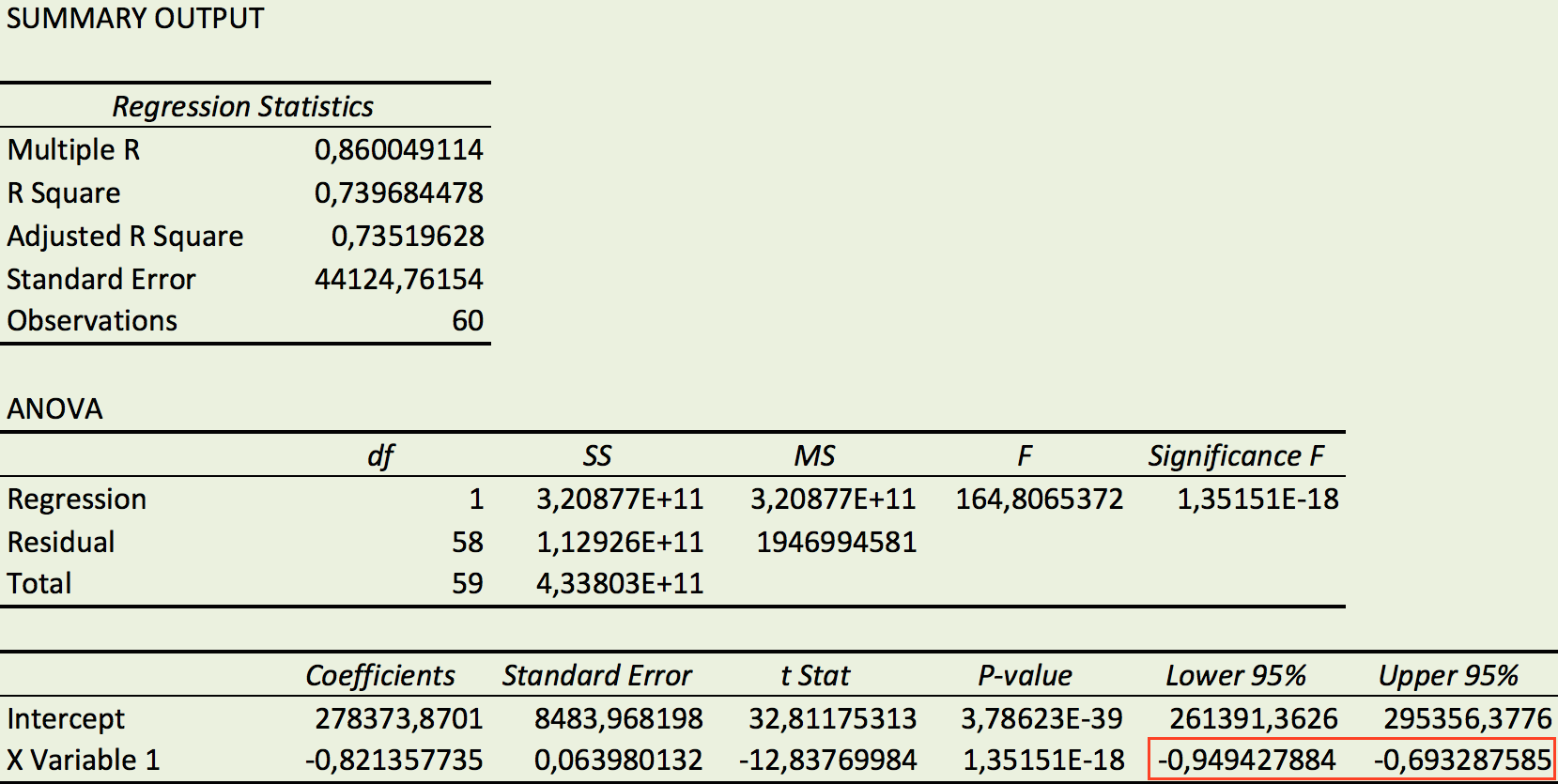
Man finder 95 %-konfidensintervallet (markeret med rødt på figuren): [-0,9494;-0,6933]
Da -1 ligger uden for konfidensintervallet er det ikke rimeligt at antage at udbudsprisen kan falde med 1 kr. pr. kørt kilometer.
-
En undersøgelse af priser for brugte biler viser, at de som nye i gennemsnit koster 278.000 kr. og at de falder med 0,8 kr. pr. kørt kilometer.

Svar på opgave 8:
-
Man skal løse ligningen f(x) = 0 med hensyn til x. Funktionen oprettes i Ti-Nspire:
f(x):=(1/3)*x3-8*x2+28*x ▸ Udført
Dernæst bruges solve-kommandoen:
solve(f(x)=0.,x) ▸ x=0. or x=4.254 or x=19.75
Dvs. nulpunkterne er x = 0, x = 4,254 eller x = 19,75
-
Man skal finde fortegn for f´(x). Man bruger solve- og derivative-kommandoerne i Ti-Nspire:
solve(derivative(f(x),x)<0.,x) ▸ 2.<x<14. (f´(x) < 0, f(x) aftagende)
solve(derivative(f(x),x)>0.,x) ▸ x<2. or x>14. (f´(x) > 0, f(x) voksende)
Dvs. f(x) er aftagende for 2 < x < 14 og voksende for x < 2 ∨ x > 14
Svar på opgave 9:
-
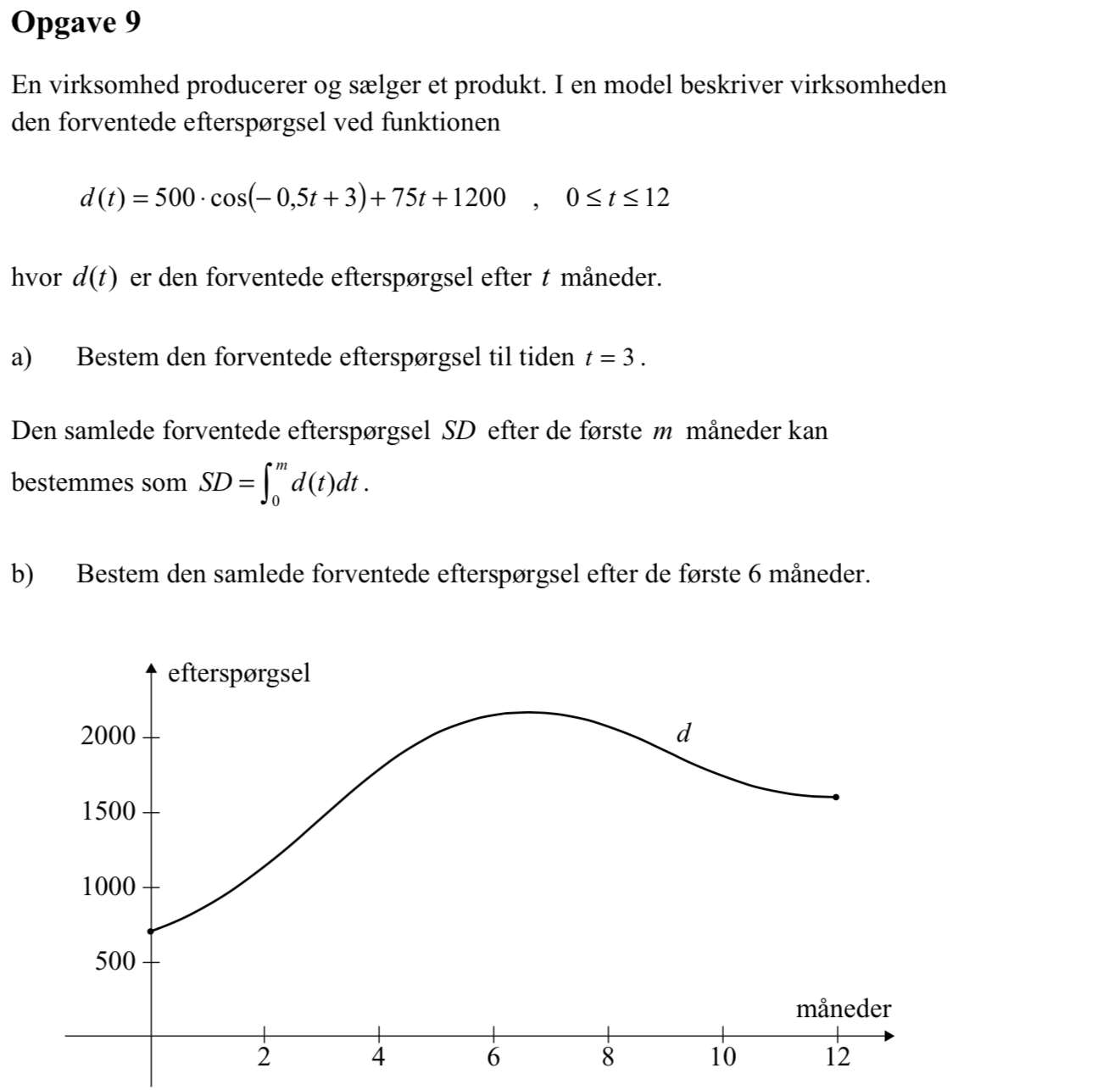
Man skal beregne d(3). Man opretter d(t) i Ti-Nspire:
d(t):=500*cos(−0.5*t+3)+75*t+1200 ▸ Udført
Det giver:
d(3) ▸ 1460.4
Dvs. efterspørgslen til tiden 3 måneder er 1.460 stk.
-
Man finder SD som integralet af d(t) fra t = 0 til t = 6. Dette gøres i Ti-Nspire:
integral(d(t),t,0,6) ▸ 8691.12
Dvs, den samlede efterspørgsel i de 6 første måneder er 8.691 stk.

Svar på opgave 10:
-
(Excel-filen, som er brugt: Fakturering.)
Man finder andelsen ved at tælle antal forekomster af "EUR" i kolonne A i Excelarket og dividere dette med 144. Dertil bruges kommandoen =TÆL.HVIS(A:A;A3)/144. Dette giver resultatet: 0,541667
Dvs. andelen p = 0,542
-
I Excel benytter man kommandoen: =1-BINOMIAL.FORDELING(71;144;0,54;SAND) som giver 0,8523.
71 er antal successer, 144 er prøvens størrelse, 0,54 er sandsynligheden for success og SAND betyder, at man akkumulerer sandsynligheden for successer fra 0 til 71. Man skal så trække dette tal fra 1 for at få den akkumulerede sandsynlighed for 72 til 144 successer.
Dvs. sandsynligheden for, at mindst halvdelen af ordrene er afgivet i euro, er 0,8523 = 85 %
Svar på opgave 11:
-
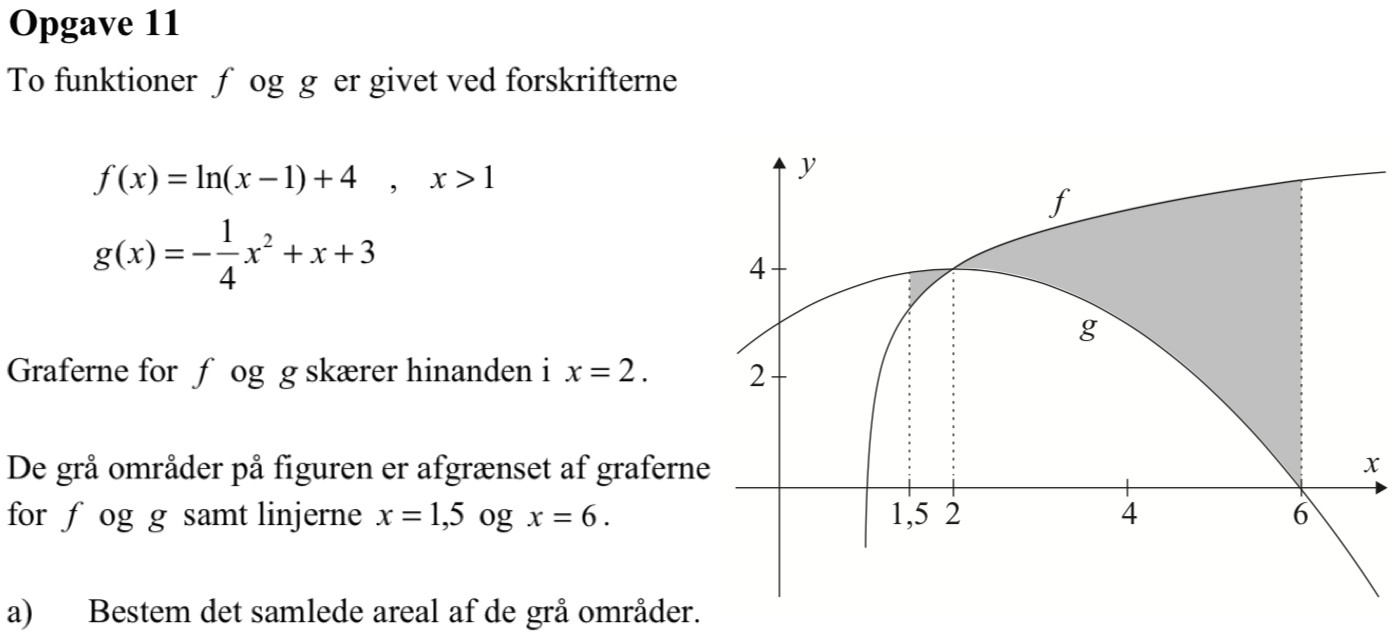
Arealet mellem kurverne er integralet af |f(x) - g(x)| fra x = 1,5 til x = 6. Man opretter f(x) og g(x) i Ti-Nspire:
f(x):=ln(x-1)+4 ▸ Udført
g(x):=(−1/4)*x2+x+3 ▸ Udført
Dernæst beregnes integralet:
Integral(abs(f(x)-g(x)),x,1.5,6) ▸ 9.5235
Dvs. arealet af det grå område er 9,52

Svar på opgave 12:
-
Dækningsbidraget ioprettes og beregnes i Ti-Nspire:
db(x,y):=−x2+800*x-0.25*y2+300*y ▸ Udført
db(300,600) ▸ 240000.
Dvs. at dækningsbidraget for x = 300 stk. og y = 600 stk. er 240.000 kr.
-
Man skal omskrive lignngen til formen: [(x-a)/b]2 + [(y-c)/d]2 = 1.
Man stater med at lave en kvadrat komplettering for led med x og y hver for sig:
Led med x: completeSquare(−x2+800*x,x) ▸ 160000-(x-400)2
Led med y: completeSquare(−0.25*y2+300*y,y) ▸ 90000.-0.25*(y-600.)2
Dette sættes ind i den oprindelige ligning:
DB(x,y) = 240000 ⇒ 160.000 - (x - 400)2 + 90.000. - 0,25*(y - 600.)2 = 240.000 ⇒
(x - 400)2 + [(y - 600)/2]2 = 10.000 ⇒ [(x - 400)/100]2 + [(y - 600)/200]2 = 1
Stillet op på den form ser man, at niveaukurven er en ellipse med centrum i (x,y) = (400,600). Desuden er lilleaksen (parallelt med x-aksen) = 100 og storaksen (parallet med y-aksen) 200.
-
Polygonområdet er tegnet i Geogebra nedenunder sammen med niveaukurven for DB(x,y)=240.000:
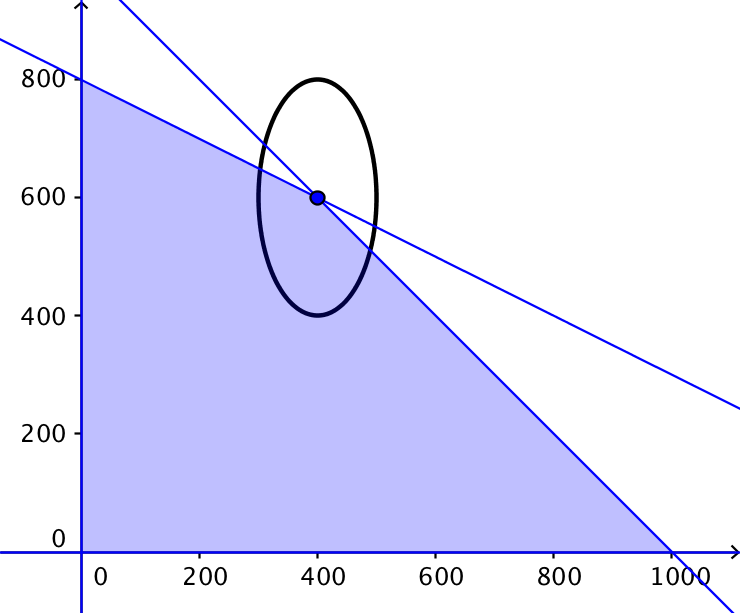
Størsteværdien antages i centrum som ligger i polygonområdet. Værdien er
DB(400,600) = 250.000 kr.


Svar på opgave 13a:
-
Man bruger annuitets-opsparingsformlen og finder ydelsen ved hjælp af solve-kommandoen i Ti-Nspire:
solve(44208.3=x*(1.042)4,x) ▸ x=37500.14
Dvs. det oprindelige beløb var 37.500 kr.
-
Man bruger gælds-annuitetsformlen og finder ydelsen i Ti-Nspire:
solve(44208.3=x*(1-1.042-5)/0.042,x) ▸ x=9986.24
Dvs. den årlige ydelse fra det indsatte beløb bliver 9.986,24 kr.

Svar på opgave 13b:
-
Man løser differentiallignigen i Ti-Nspire:
deSolve(p'=−0.82*(1/x),x,p) ▸ p=c1-0.82*ln(x)
Dvs. den fuldstændige løsning er p(x) = C - 0,82·ln(x)
-
Man skal finde C i den fuldstændige løsning, når der gælder, at p(10000) = 89. Dette løses med solve i Ti-Nspire:
solve(c-0.82*ln(10000)=89,c) ▸ c=96.552
Dvs. forskriften for p bliver: p(x) = 96,55 - 0,82·ln(x)
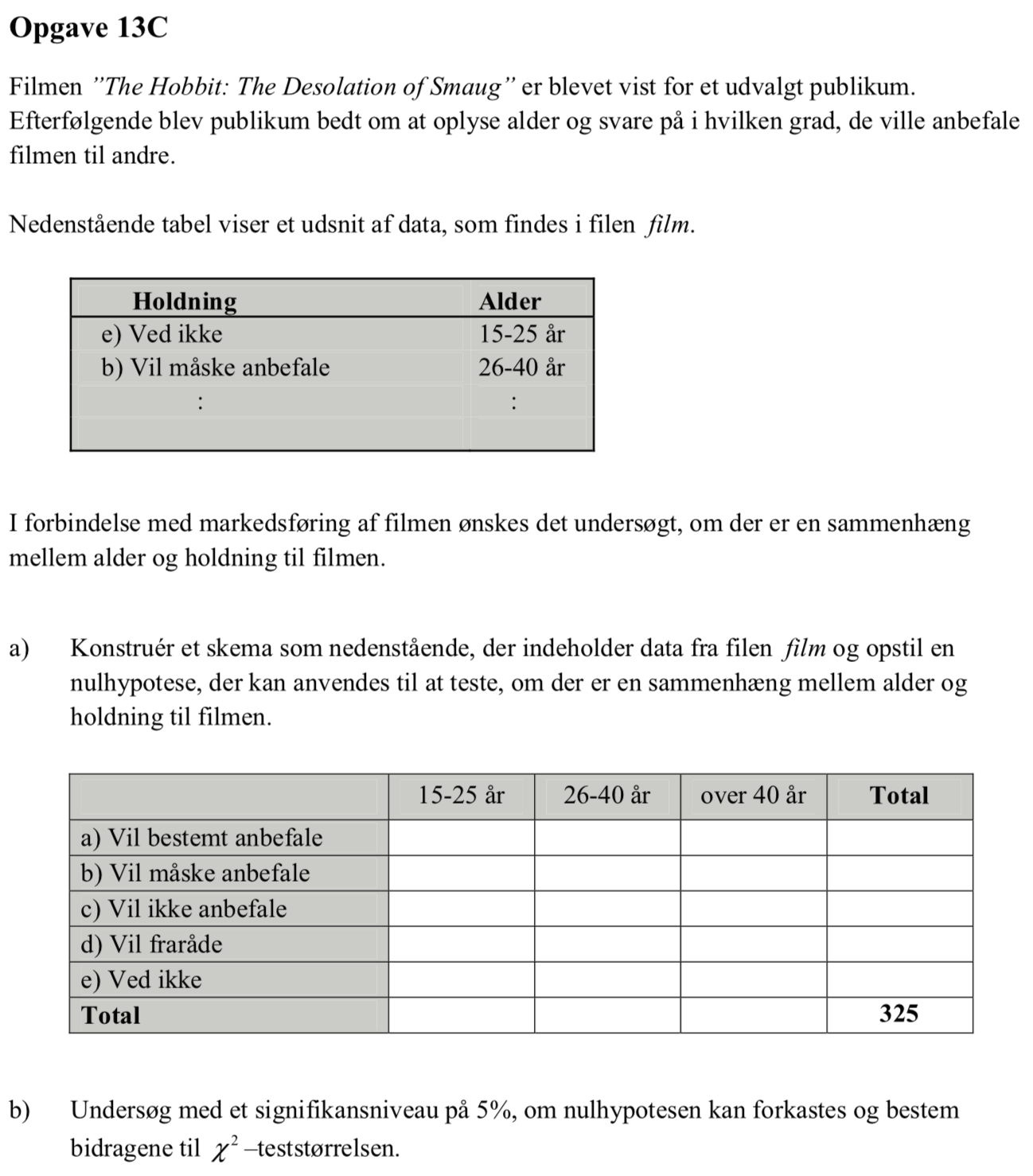
Svar på opgave 13c:
-
Man laver nedenstående skema kaldet "Observeret" ved hjælp af TÆL.HVISER kommandoen i Excel. (De formler, som er anvendt, kan se i Excel-filen Film.)
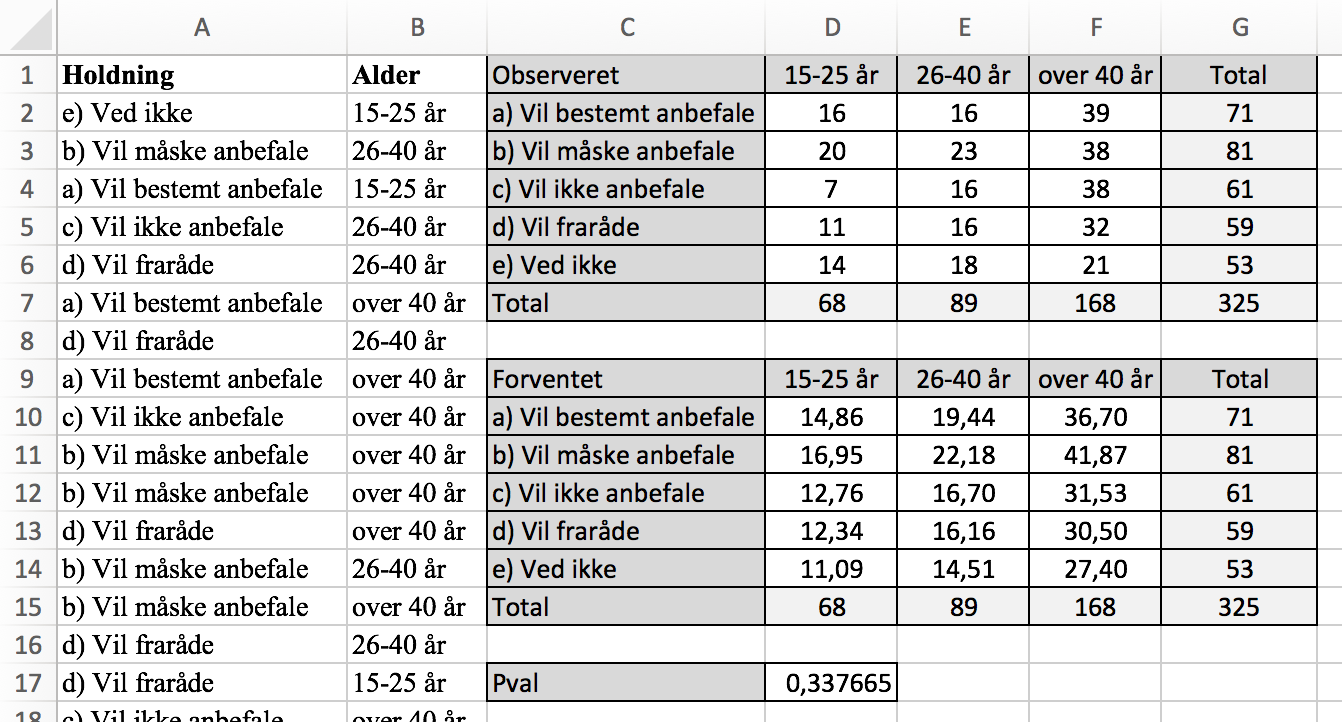
Nulhypoteen er at "overskrifter lodret" er uafhængige af "overskrifter vandret", dvs. at alder er uafhængig af holdning til filmen (eller omvendt: holdning til filmen er uafhængig af alder). Desuden kan man sige, at afvigelser mellem obeserverede og forventede data kan forklares med tilfældigheder.
Et siknifikansniveau på 5 % betyder i den forbindelse, at der er 5 %'s sandsynlighed for, at afvigelser mellem observerede værdier og forventede ikke kan forklares med tilfældigheder. Hvis der er mindre end 5%'s sandsynlighed for dette forkastes hypotesen.
-
Billedet ovenfor viser en tabel over forventede værdier, hvor hver værdi findes ud fra summerne i skemaet med observerede værdier.
En CHI-i-anden test med 8 frihedsgrader giver resultatet 0,34, som er større end 5 % = 0,05, hvilket vil sige, at nulhypotesen accepteres.