
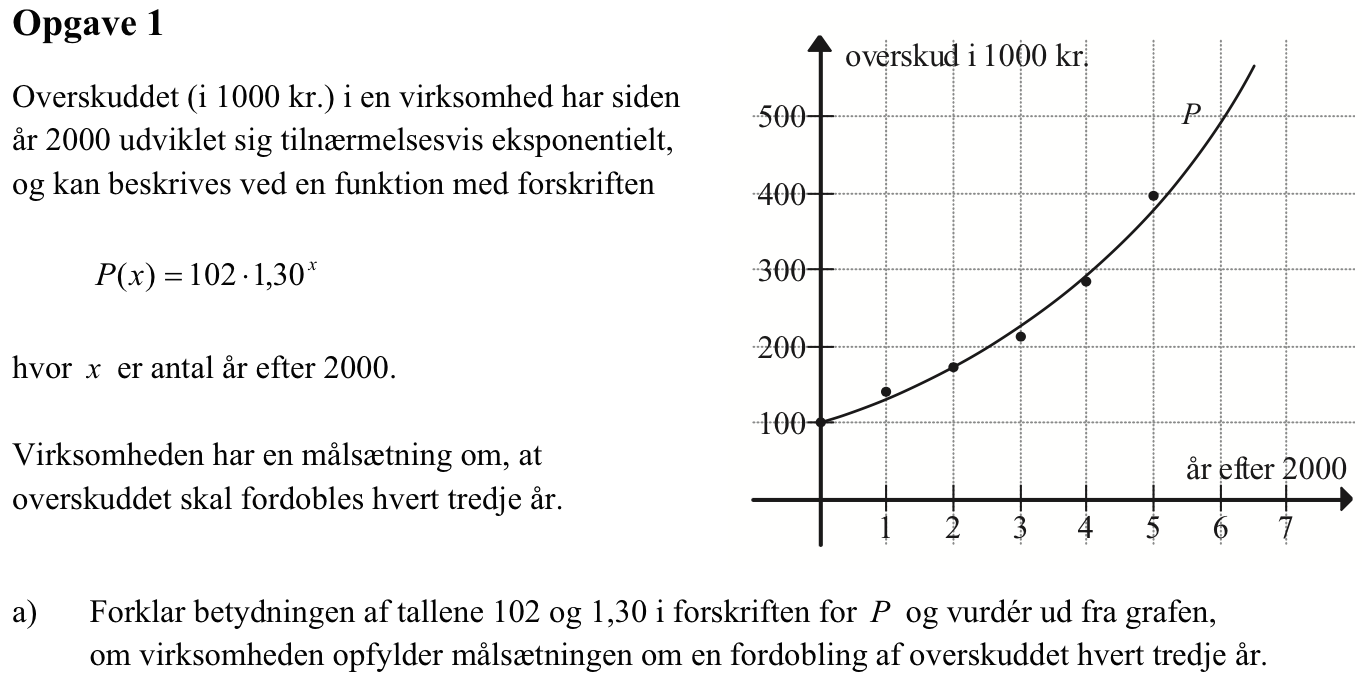
Svar på opgave 1:
-
Tallet 102 er startværdien, dvs. overskuddet er 102.000 kr. år 2000. Tallet 1,30 er fremskrivningsfaktoren dvs. det man skal gange sidste års overskud med for at få dette års overskud.
Ved at se på grafen kan man se at overskuddet er ca. 100.000 i år 0 og at det 3 år efter er lidt over 200.000. Dermed ser det ud til at passe, at det mere end fordobles hvert 3. år.
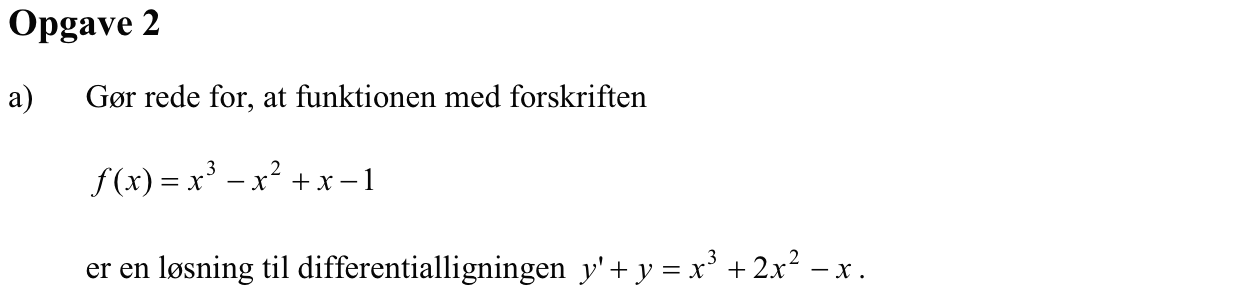
Svar på opgave 2:
-
At vise at f(x) er en løsning til differentialligningen y' + y = x3 + 2x2 + x, betyder at man skal indsætte f(x) i stedet for y i differentialligningen og f´(x) i stedet for y' og gøre prøve, dvs. undersøge om venstre side og højre side af differentialligningen giver det samme ved indsættelsen.
Man får at f´(x) = 3x2 - 2x + 1. Dette indsættes sammen med f(x) = x3 - x2 + x - 1. Dette giver venstre og højre side:
Venstre: 3x2 - 2x + 1 + (x3 - x2 + x - 1) = x3 + 2x2 + x
Højre: x3 + 2x2 + x
Da venstre og højre side er ens, er det bevist, at f(x) er en løsning til differentialligningen.

Svar på opgave 3:
-
Arealet af det grå område er integralet af f(x) fra x = 0 til x = 1. Dvs. arealet er:
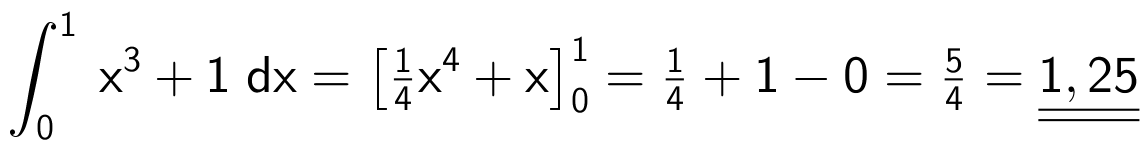

Svar på opgave 4:
-
Nedenstående graf til f(x) er lavet i Excel.
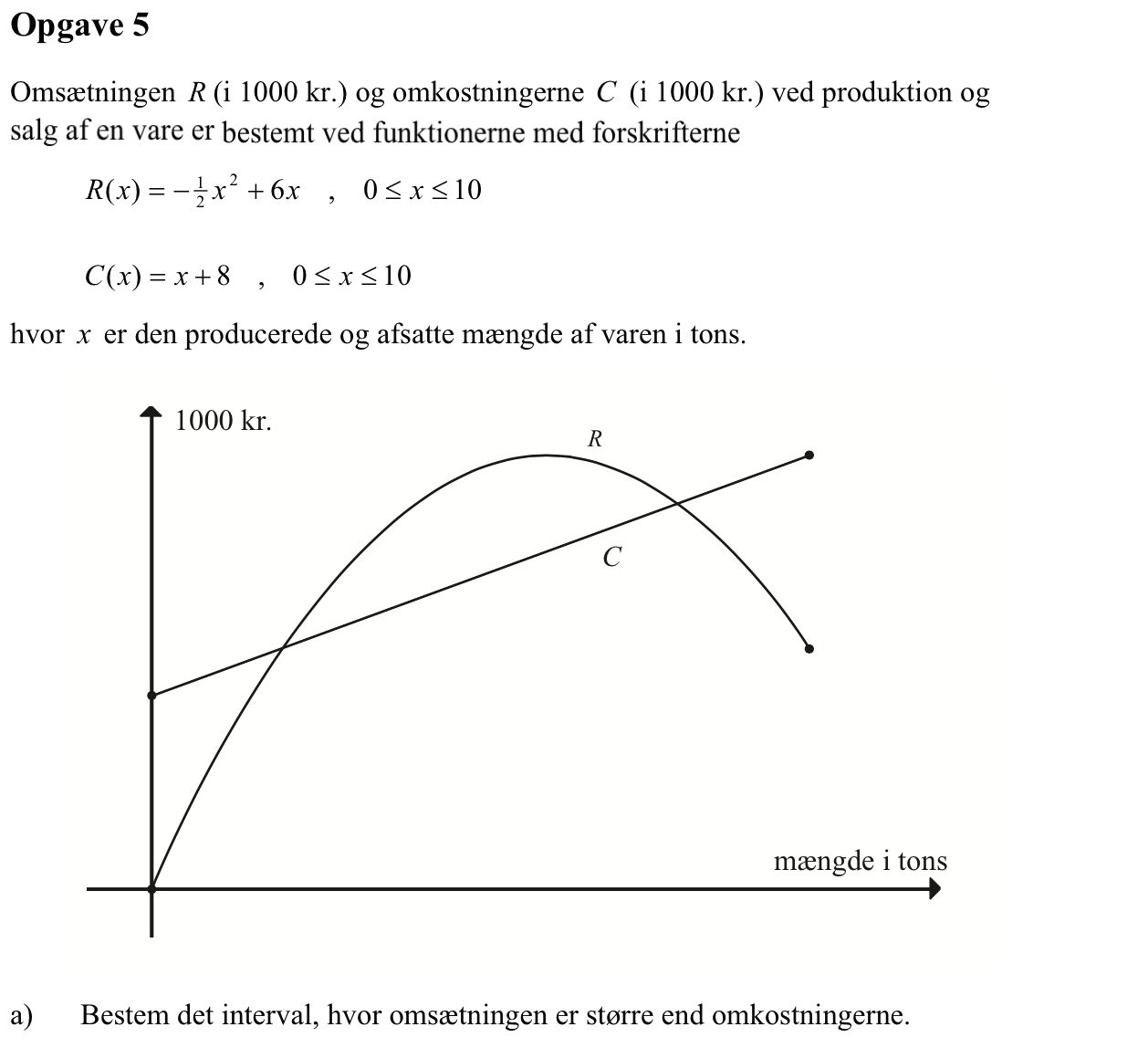
Svar på opgave 5:
-
Man skal løse uligheden R(x) > O(x) i intervallet 0 ≤ x ≤ 10. Dette giver en andengrads-ulighed i x:
-0,5·x2 + 6·x > x + 8 ⇒ -0,5·x2 + 5·x - 8 > 0
Man løser nu den tilsvarende andengradsligning: -0,5·x2 + 5·x - 8 = 0. Der vil gælde at de x, der opfylder uligheden, vil ligge mellem løsningerne til andengradsligningen, da y = -0,5·x2 + 5·x - 8 er en parabel, der vender grenen nedad, og som derfor er større end 0 mellem sine nulpunkter. Man får:
-0,5·x2 + 5·x - 8 = 0 ⇒
x = -(5/-1) ± √(25 - 16) ⇒
x = 5 ± 3 ⇒
x = 2 ∨ x = 8
Dvs. omsætningen er større end omkostningerne for 2 tons < x < 8 tons



Svar på opgave 6:
-
Man finder a ved hjælp af solve- og integral-kommandoerne i Ti-Nspire:
solve(Integral(sqrt(x+a),x,0,15)=42,a) ▸ a=1
Dvs. den a-værdi, der opfylder betingelsen er a = 1
-
2. Man indsætter udtrykket for f(x,y) på venstre side af lighedstegnet
3. Man sætter 4 uden for en parantes af led, der indeholder y
4. Man laver kvadratkomplettering med hensyn til x og y
5. Man samler konstante led på højre side af lighedstegnet
6. Man dividerer igennem med de 10.000, der står på højre side af lighedstegnet, og omskriver nævnerne på venstre side til kvadrater.

Svar på opgave 7:
-
Nedenstående sumkurve er tegnet i Excel. Lønsummerne er inddelt i intervaller på 5 fra 45 til 95, lønsummer mindre end de viste grænser er lagt sammen og afbildet ud for grænsen.
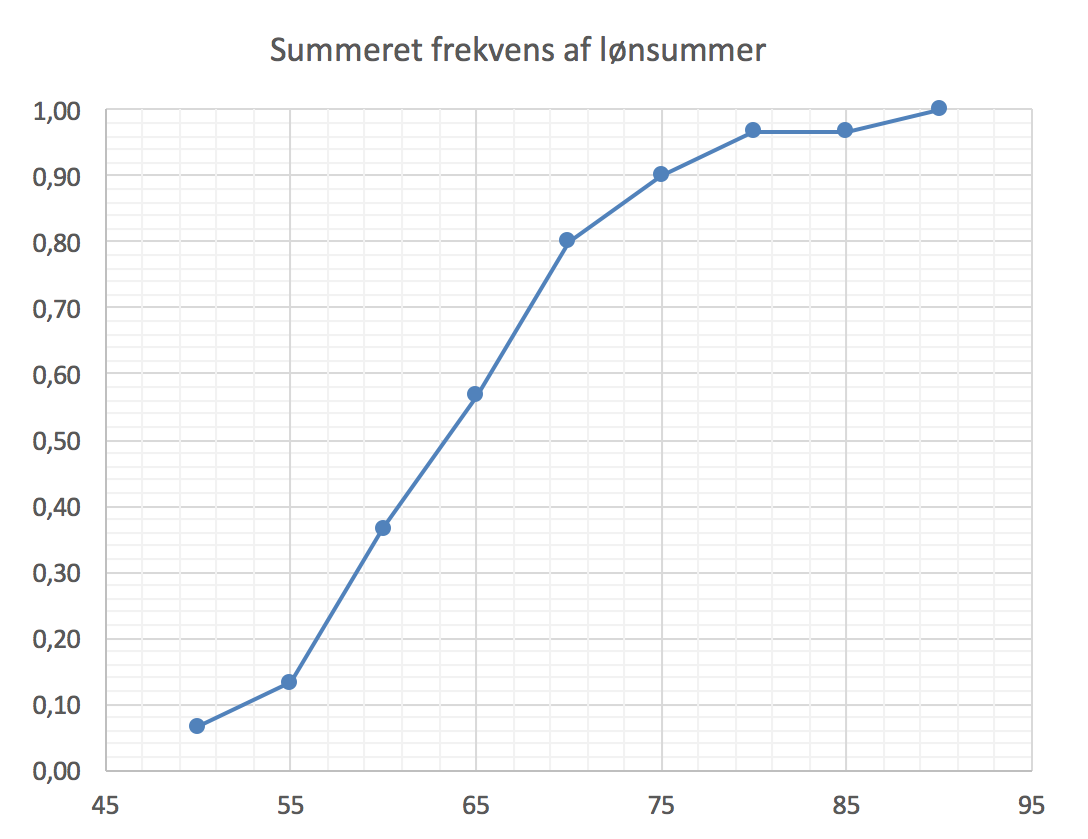
-
Man bruger Excel-kommandoen Funktioner - Dataanalyse - Deskriptiv Statistik og får:
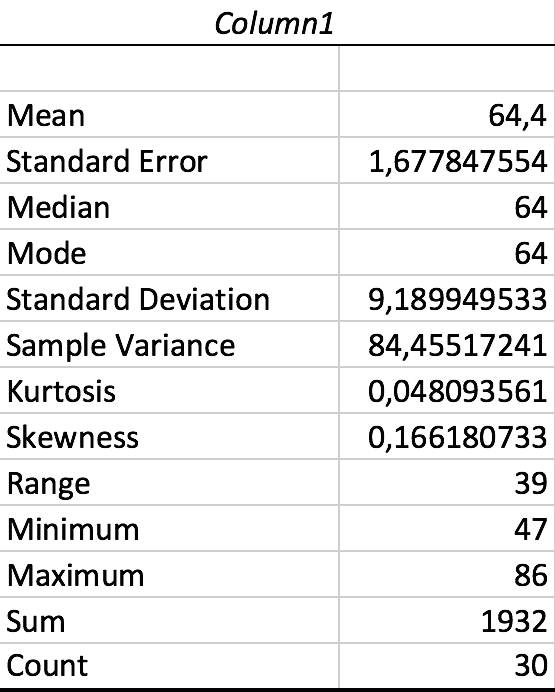
Mer af ses at median er 64, middel er 64,4 og standardafvigelse er 9,19
-
Nedenstående punktplot er tegnet i Excel. Det viser lønsummen for de enkelte klubber (y) som funktion af antal sejre for klubben (x).
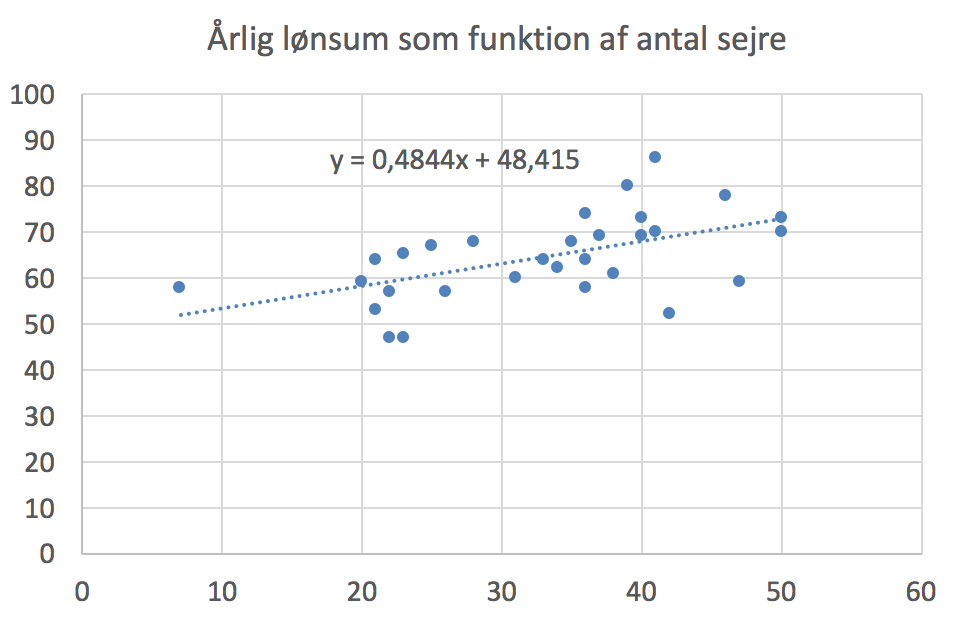
Den lineære regtressionsmodel er fundet som tendenslinjen i Excel og aflæses til: y = 0,4844x + 48,415
-
Baseret på grafen ser man at der er en tendens til at lønnen stiger med antal sejre omend svagt og med en forhold for usikkerhed i tallene. Forskellen på mindst vindende hold og mest vindende er $ 20 mio.
(Se også Excelfilen NBA)
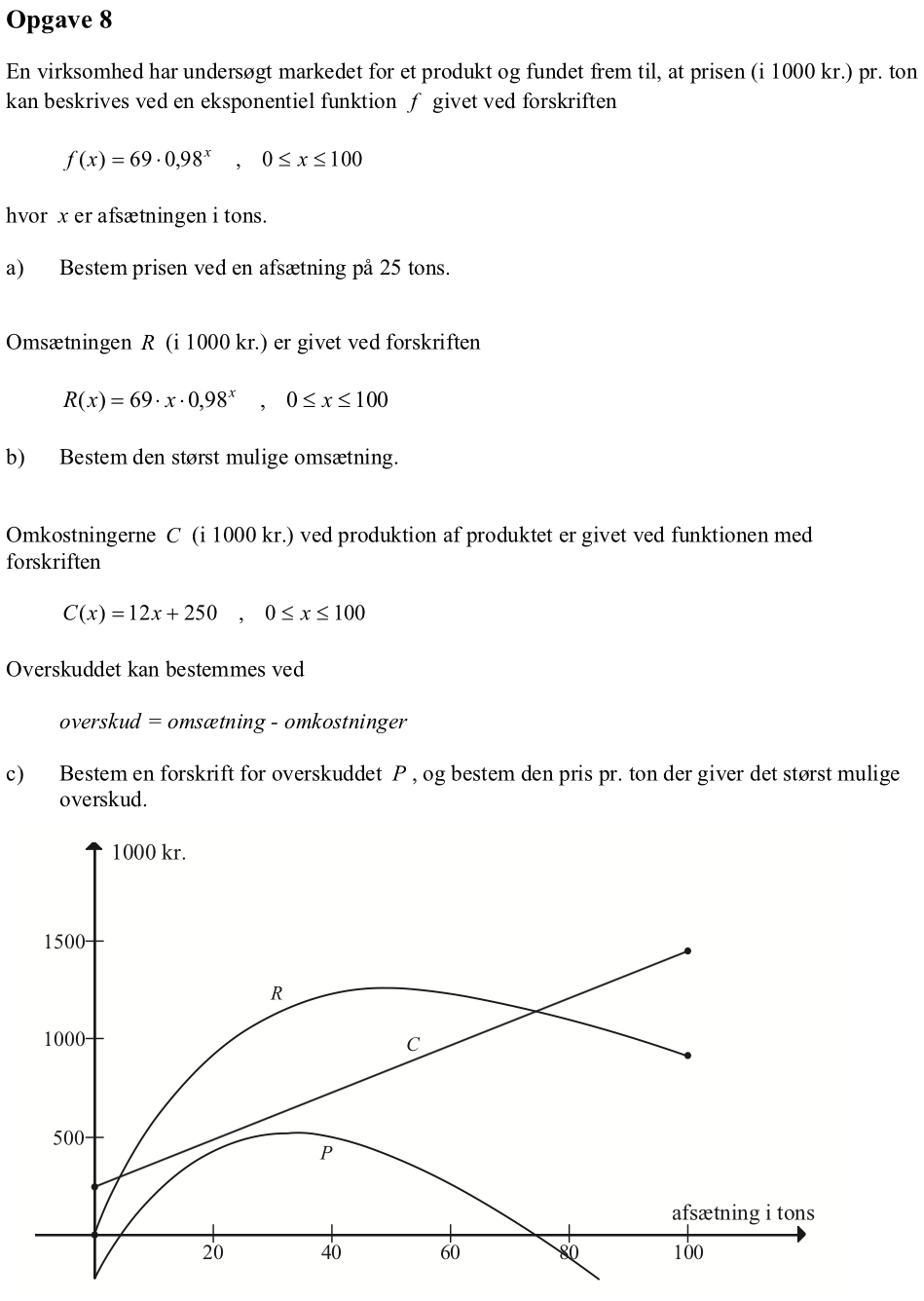
Svar på opgave 8:
-
Man skal finde f(25). Først oprettes funktionen i Ti-Nspire:
f(x):=69*0.98x ▸ Udført
Dernæst beregnes prisen:
f(25) ▸ 41.639
Dvs. prisen pr. ton er 41639 kr.
-
Man opretter R(x) i Ti-Nspire:
r(x):=69*x*0.98x ▸ Udført
Herefter finder man det x, der giver størsteværdien:
fMax(r(x),x) ▸ x=49.498
Dette indsættes i R(x) for at finde størsteværdien:
r(49.498) ▸ 1256.449
Dvs. den størst mulige omsætning er 1.256.449 kr.
-
Man opretter C(x) og P(x) i Ti-Nspire:
c(x):=12*x+250 ▸ Udført
p(x):=r(x)-c(x) ▸ Udført
Man finder dernæst det x, der giver den største værdi af P(x):
fMax(p(x),x) ▸ x=32.799
Dette x indsættes i f(x) for at få den pris, der giver det største overskud:
f(32.799) ▸ 35.569
Dvs. den pris, der giver størst overskud, er 35569 kr. pr. ton
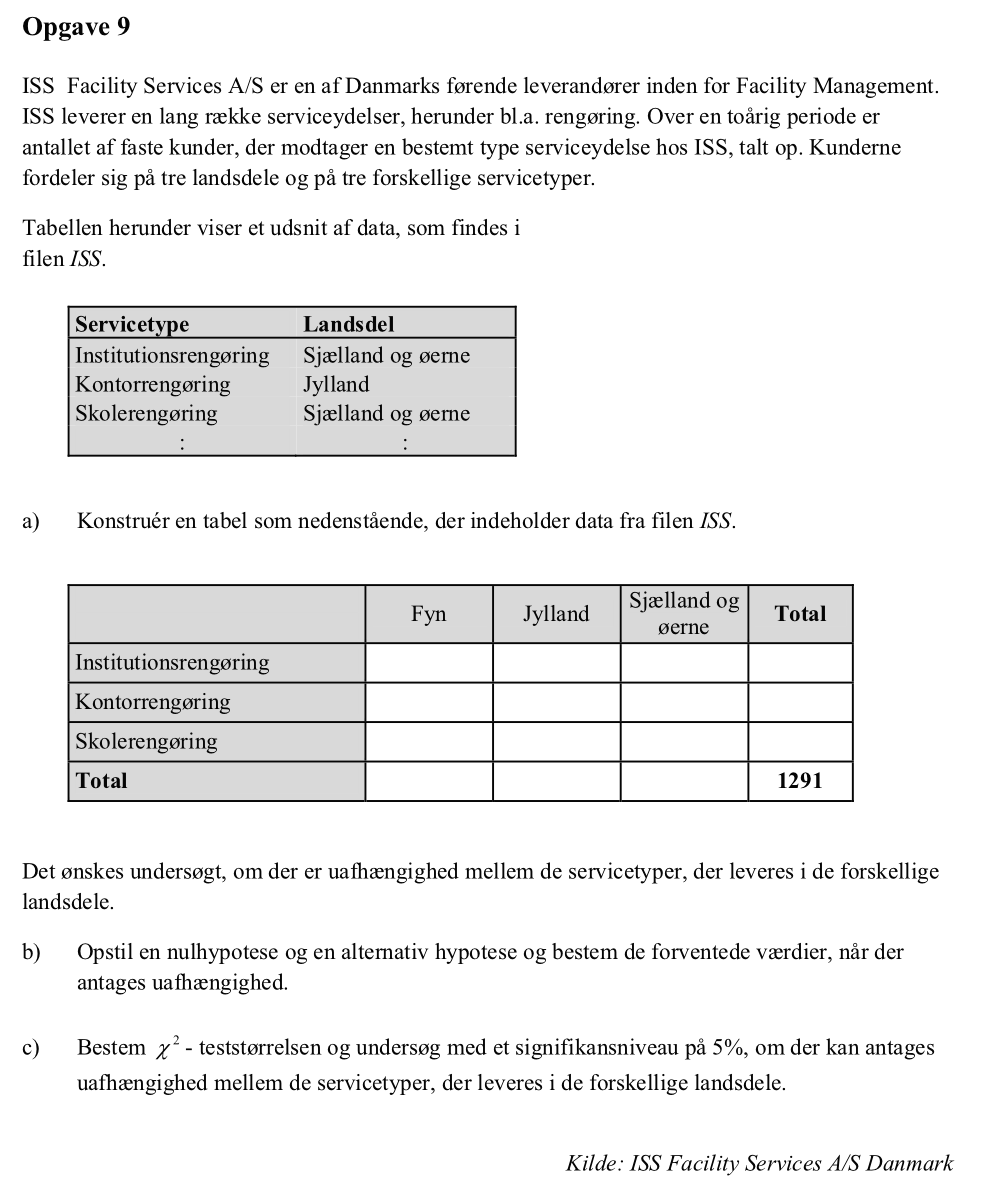
Svar på opgave 9:
-
I Excel får man:
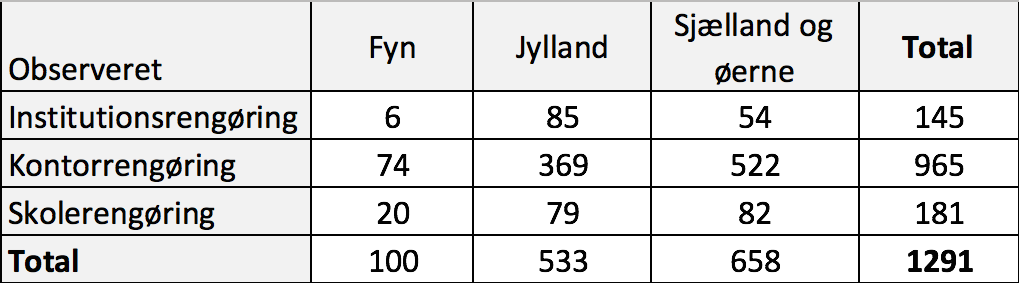
-
Nulhypotesen er at den leverede servicetype er uafhængig af landsdel. Alternative hypoteser er, at det ikke gælder.
Man finder de forventede værdier ud fra summerne i tabellen med observerede værdier:
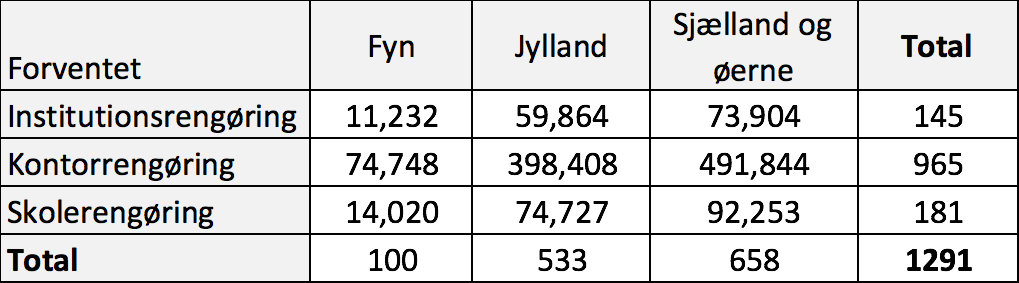
-
Man laver en Chi-i-anden test i Excel og får resultatet PVal = 2,737·10-5, som er mindre end 5% og dermed er nulhypotesen forkastet.
(Se også Excel filen ISS under regnearket "Svar".)

Svar på opgave 10:
-
Man løser differentialligningen i Ti-Nspire med følgende kommando:
deSolve(y'=−0.05*y+10 and y(0)=0,x,y) ▸ y=200.-200.*0.9512x
Dvs. at A(x) = 200 - 200·0,9512x
-
Man skal finde A(30), det gøres i Ti-Nspire:
200.-200.*0.951229x|x=30 ▸ 155.37
Dvs. afsætningen efter 30 dage er 155370 stk.
Svar på opgave 11:
-
Vendetangenten findes for f´´(x) = 0. Man får at f´´(x) = -2x + 12. f´´(x) = 0 ⇒ -2x + 12 = 0 ⇒ x = 6
Tangenten gennem punktet (6,f(6)) har ligningen: y = f´(6)·(x - 6) + f(6), f´(x) = -x2 + 12x - 32. Dette giver: f´(6) = -(6)2 + 12·6 - 32 = -36 + 72 - 32 = 4. f(6) = -⅓·63 + 6·62 - 32·6 + 60 = 12. Man får tangentligningen:
y = 4·(x - 6) + 12 = 4x - 12
-
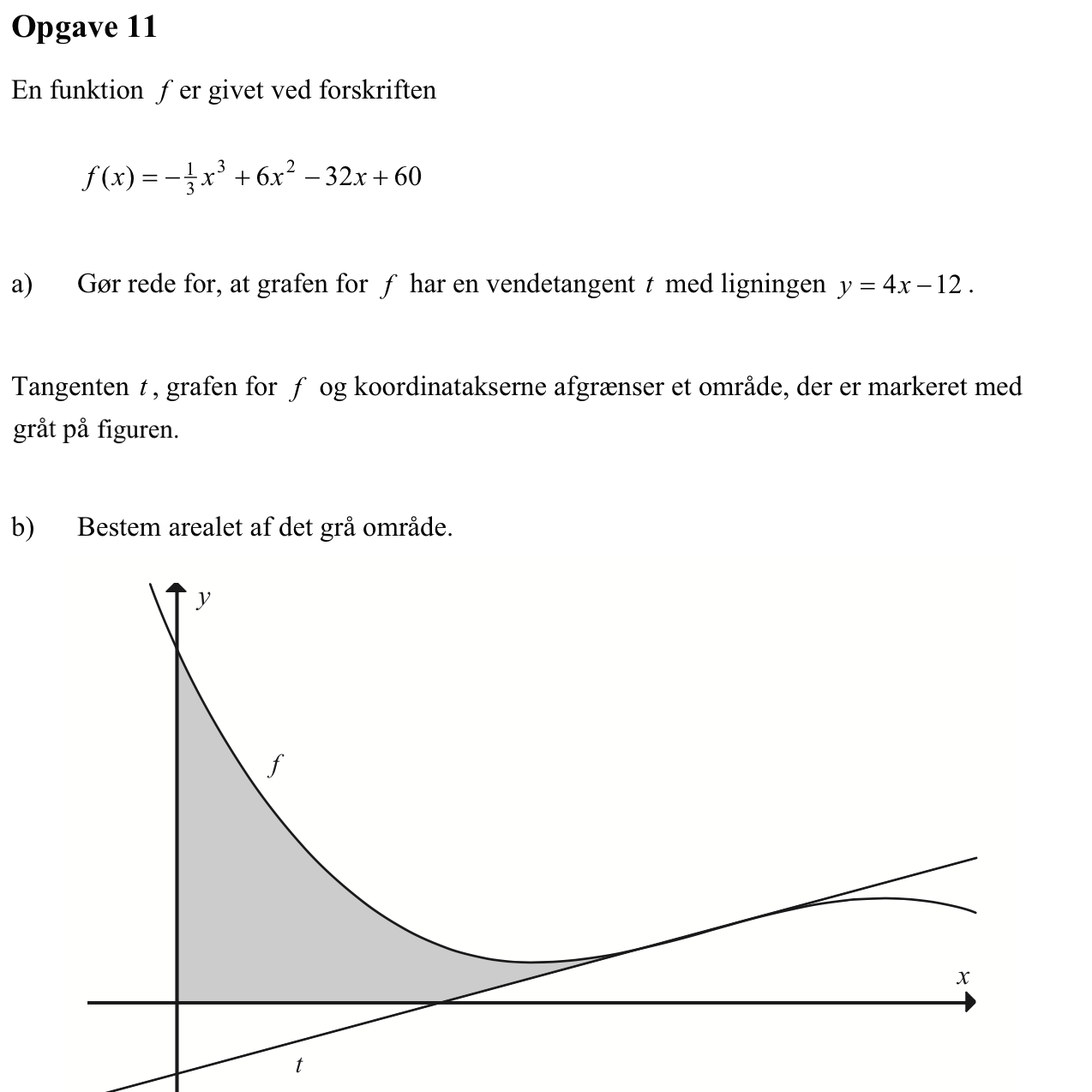
For at finde arealet af det grå område skal man finde det punkt, hvor tangenten skærer x-aksen. Man får: 4x - 12 = 0 ⇒ x = 3.
Man indfører funktionen g(x) = 4x - 12 og får formlen for arealet:
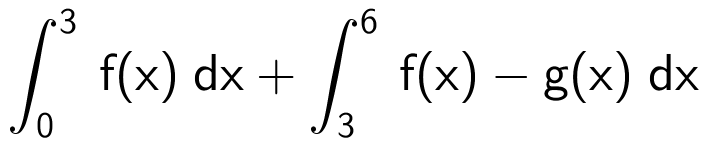
Dette beregnes i Ti-Nspire:
Integral(f(x),x,0,3) + Integral(f(x)-g(x),x,3,6) ▸ 90
Dvs. arealet af det grå område er 90


Svar på opgave 12a:
-
Man bruger formlen for ydelse for annuitetslån: ydelse = G·r/(1-(1+r)-n), hvor G er det lånte beløb, r er rentesatsen og n er antal terminer. Man får:
y = 175000·0,022/(1-(1,022)-10) = 19686,56
-
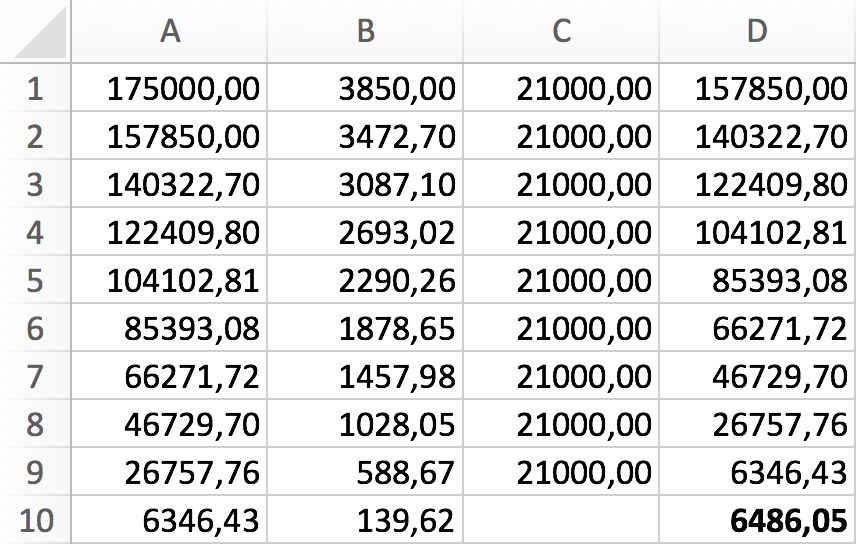
Man beregner det betalte beløb efter 9 år med en ydelse på 21000 kr. ved hjælp af formlen for restgælden af et annuitetslån: Restgæld = G·(1 + r)n - y·[(1 + r)n - 1]/r
Dette giver: restgæld = 175000·1,0229 - 21000·[1,0229 - 1]/0,022 kr. = 6346,43 kr.
Af denne restgæld betales der rente og dette beløb lagt til restgælden efter ni år giver sidste ydelse:
6346,43·1,022 kr. = 6486,05 kr.
Sidste ydelse beregnet i Excel:

Svar på opgave 12b:
-
Den estimerede værdi for p = 450/1500 = 0,3.
95%-konfidensintervallet er [0,3 - 1,96·√(0,3·0,7/1500); 0,3 + 1,96·√(0,3·0,7/1500)] = [0,2768; 0,3232]
Købmandens mælp kan godt have samme andel af økologisk mælk som på landsplan.
-
Man skal finde P(X > 450) i en binomialfordeling med p = 0,28 og n = 1500. Dette beregnes i Ti-Nspire:
binomCdf(1500,0.28,450,1500) ▸ 0.04562
Dvs. sandsynligheden for at der er mindst 450 L økologisk mælk i prøven er 0,046.

Svar på opgave 12c:
-
Formlen for niveau-kurven for dækningsbidraget kan generelt skrives: -0,04·x2 + 60x + 5y - 1000 = t ⇒ y = 0,008·x2 - 12x + 200 + t/5.
Derfor har punktmængden eller niveaukurven N(20000) formlen: y = 0,008·x2 - 12x + 200 + 20000/5 ⇒ y = 0,008·x2 - 12x + 4200.
Dette er formlen for en parabel. Niveaukurven for N(20000) er tegnet herunder i Geogebra.
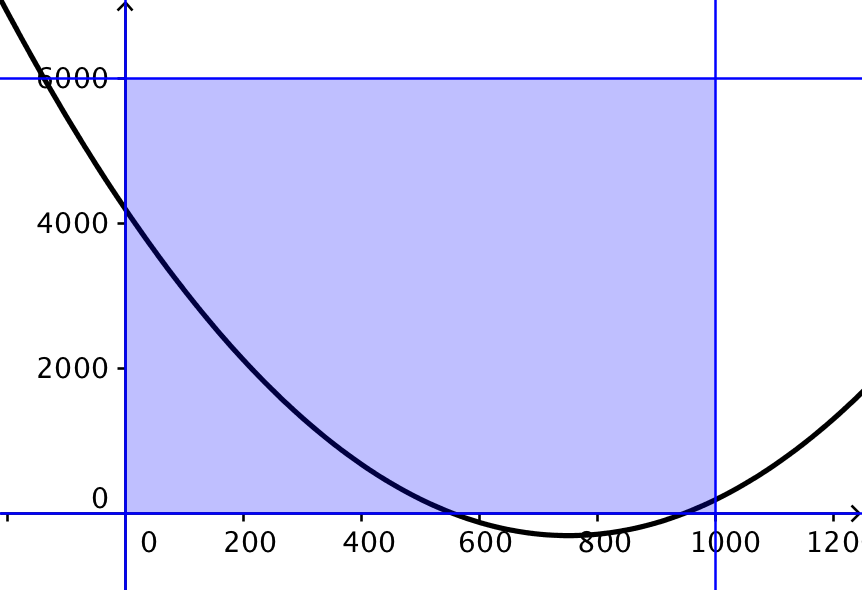
Begrænsningerne er: 0 ≤ x ≤ 1000 og 0 ≤ y ≤ 6000.
-
Når man man øger t, får man niveaukurven for et stadig større dækningsbidrag. En forøgning af t svarer til en parallelforskydning af parablen, som er niveaukurven for dækningsbidraget.
Man skal finde den parabel, der tangerer polygon-området, når man parallelforskyder parablen som vist på tegningen nedenunder:
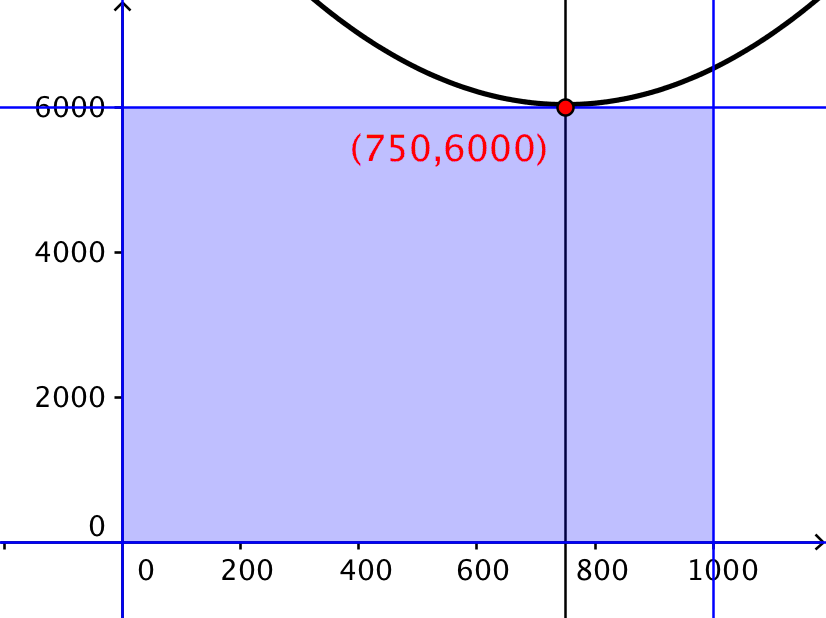
Dette giver det optimale antal A = 750 og det optimale antal af B = 6000.
Det optimale dækningsbidrag er -0,04·7502 + 60·750 + 5·6000 - 1000 kr. = 51500 kr.