Svar på opgave 1:

1. Det indsatte beløb findes som K i ligningen: K·(1+3,5%)⁵ = 59.384,32.

   Man får følgende i Ti-Nspire: solve(k*(1+(3.5)%)⁵=59384.32,k) ▸ k=50000.

   Dvs. det indsatte beløb var 50000 kr.

2. Rentesatsen findes som r i ligningen: 100000·(1+r)⁵=125000.

   Man får følgende i Ti-Nspire: solve(100000*(1+r)⁵=125000.,r) ▸ r=0.04564

   Dvs. rentesatsen er 4,56 %

Svar på opgave 2:

1. -40900 er den årlige ændring af medlemstallet. Dvs. at der er en årlige nedgang i medlemstallet på 40900. 1400000 er medlemstallet for x = 0, dvs. medlemstallet i 2004.

2. For at finde årstallet skal man løse ligningen -40900·x + 1400000 = 1000000 med hensyn til x:

   −40900x + 1400000 = 1000000 ⇒ x = 9,78

   Dvs. det årstal, hvor 1.000.000 medlemmer passeres er 2004 + 10 = 2014

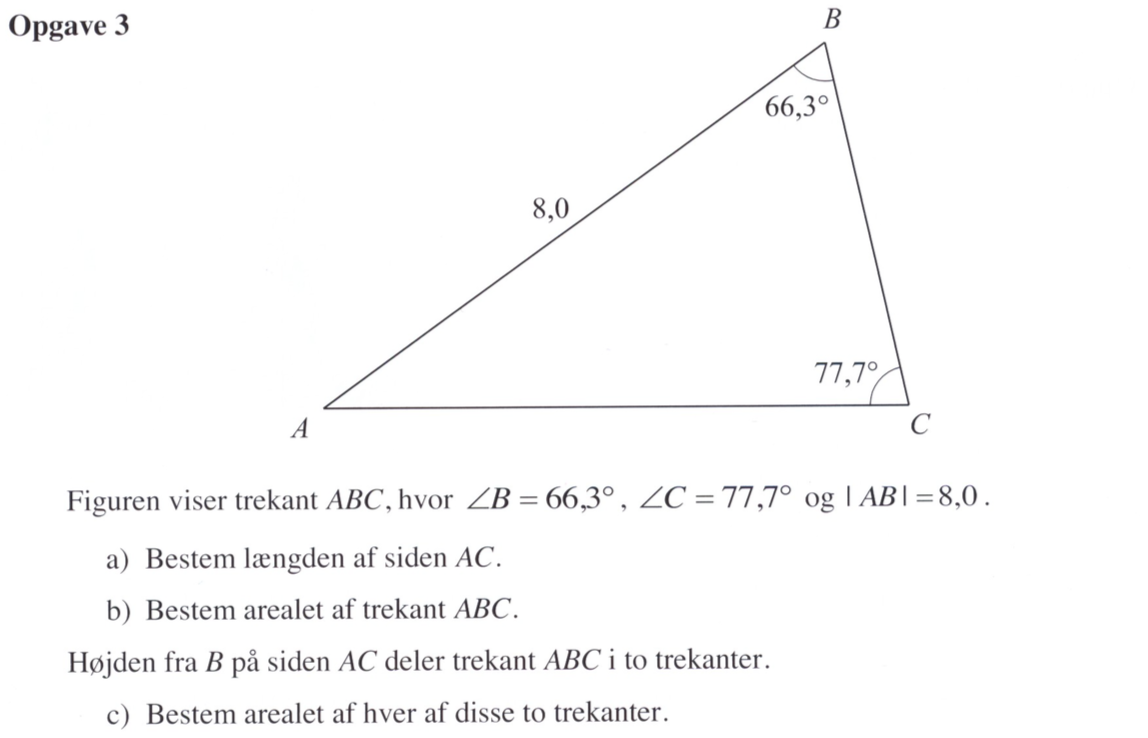
Svar på opgave 3:

1. |AC| bestemmes ved hjælp af en sinusrelation. Dette gøres i TI-Nspire:

   solve(8./sin(77.7°)=ac/sin(66.3°),ac) ▸ ac=7.4974

   Dvs. |AC| = 7,50

2. Arealet af trekant ABC er 0,5·grundlinje·højde = 0,5·|AC|·[8,0·sin(A)] = 0,5·|AC|·8,0·sin(180°-66,3°-77,7°) = 0,5·7,4974·8·sin(36°) = 17,627.

   Dvs arealet af trekant ABC er 17,6

3. Højdens fodpunkt på AC kaldes H som vist nedenfor. AH og BH er kateter i ABH. |AH| = 8,0·cos(36°).

   

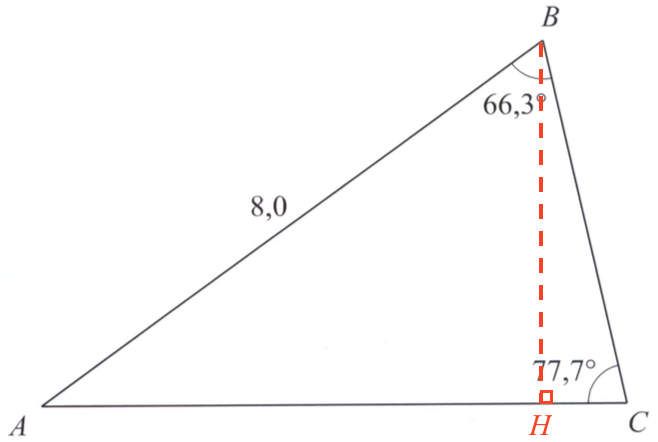
   Arealet af trekant ABH er 0,5·|AH|·|BH| = 0,5·8·cos(36°)·8·sin(36°) = 15,2

   Arealet af trekant BCH er 17,6274 - 15,2169 = 2,41

Svar på opgave 4:

1. Vægten af en 23 cm lang bækforel er: 0,0117·23^2,97 g = 129,6 g

2. Man skal bruge formlen for procent-procentvækst for potensfunktioner: (1,25^2,97-1)·100 % = 94,01 %.

   Dvs. den store bækforel er 94 % større end den lille.

Svar på opgave 5:

1. Man sætter nedre gænse for første interval til 2,0 og øvre grænse for sidste interval til 5. Det antages at ingen fødselesvægt ligger under 2 kg.

   Frekvenserne beregnes ud fra procenterne ved at dividere med 100. Frekvenserne lægges sammen, så man får de kummulerede frekvenser:

   0; 0,051; 0,174; 0,493, 0,828; 0,969 og 1,0. Dette giver sumkurven:

   

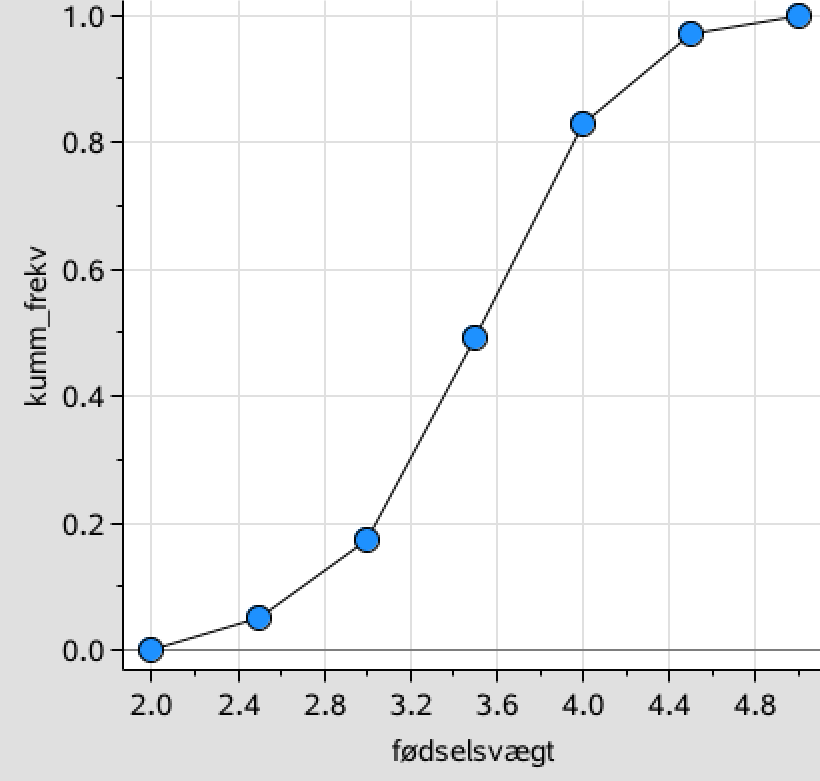
2. Procentdelen af børnene, som vejer over 3,8 kg, beregnes ved hjælp af sumkurven:

   

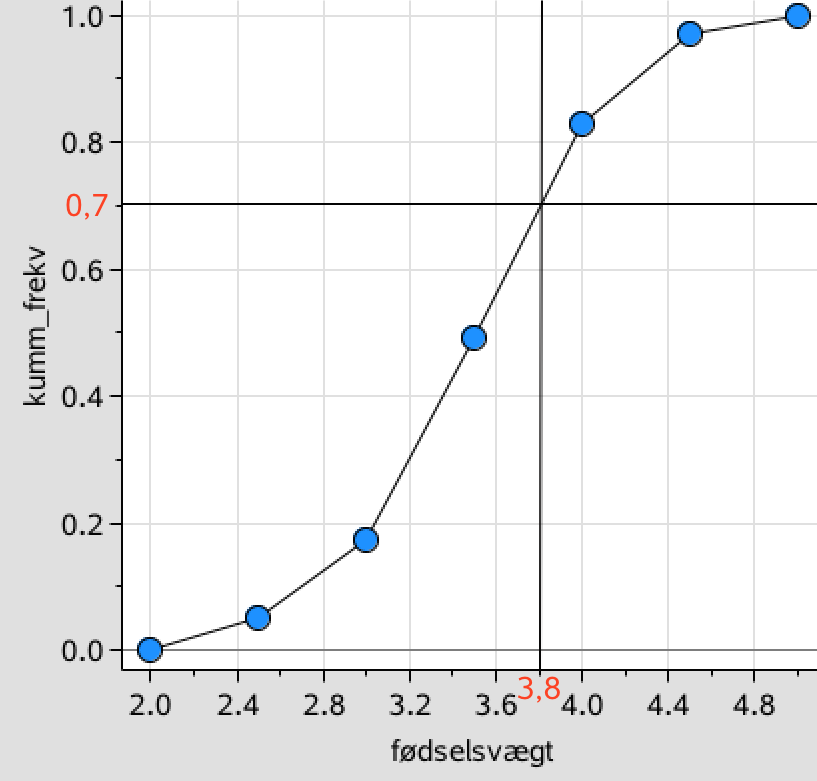
   Af sumkurven ses, at 70 % (y-aksen) af børnene vejer under 3,8 kg (x-aksen).

   Dette giver, at 100 % - 70 % = 30 % vejer over 3,8 kg.

Svar på opgave 6:

1. Man løser de sammenhørende ligninger: 3280 = b·a⁰ ∧ 10000 = b·a⁵ med hensyn til a og b. Dette gøres i Ti-Nspire:

   solve(3280=b*a⁰ and 10000.=b*a⁵,a,b) ▸ a=1.24976 and b=3280.

   Dvs. a = 1,250 og b = 3280

2. I år 2010 er x = 10 (2010 - 2000). Dette indsættes i forskriften: 3280·1,24976¹⁰ = 30488.8.

   Dvs. antallet af parakitter i 2010 er 30.489

3. Fordoblingstiden er ln(2)/ln(1.24976) år = 3,10896 år = 3,1 år

Svar på opgave 7:

1. Der gælder at forholdet: (antal familier et bestemt år)/(indeks et bestemt år) skal være det samme for alle år.

   Man sætter antal familier (i tusinder) med mere end en bil i 2009 = x. Man får: 364/100 = x/103,8 ⇒ x = 377,8.

   Dvs. antal familier med mere end en bil i 2009 = 378.000

   Man får for året 2007: 340/(indeks for 2007) = 364/100 ⇒ indeks for 2007 = 93,4