Svar på opgave 1:

1. Vægten af kyllingen efter 21 dage er (40 + 21·35) g = 775 g

   Forskriften er f(x) = 35x + 40, hvor f(x) er vægten af kyllingen og x er antallet af dage, som den har levet.

2. For at finde ud af hvor længe kyllingen lever, skal man løse ligningen f(x) = 2500 ⇒ 35x + 40 = 2500 ⇒ x = 70,29.

   Dvs. kyllingen lever 70 dage

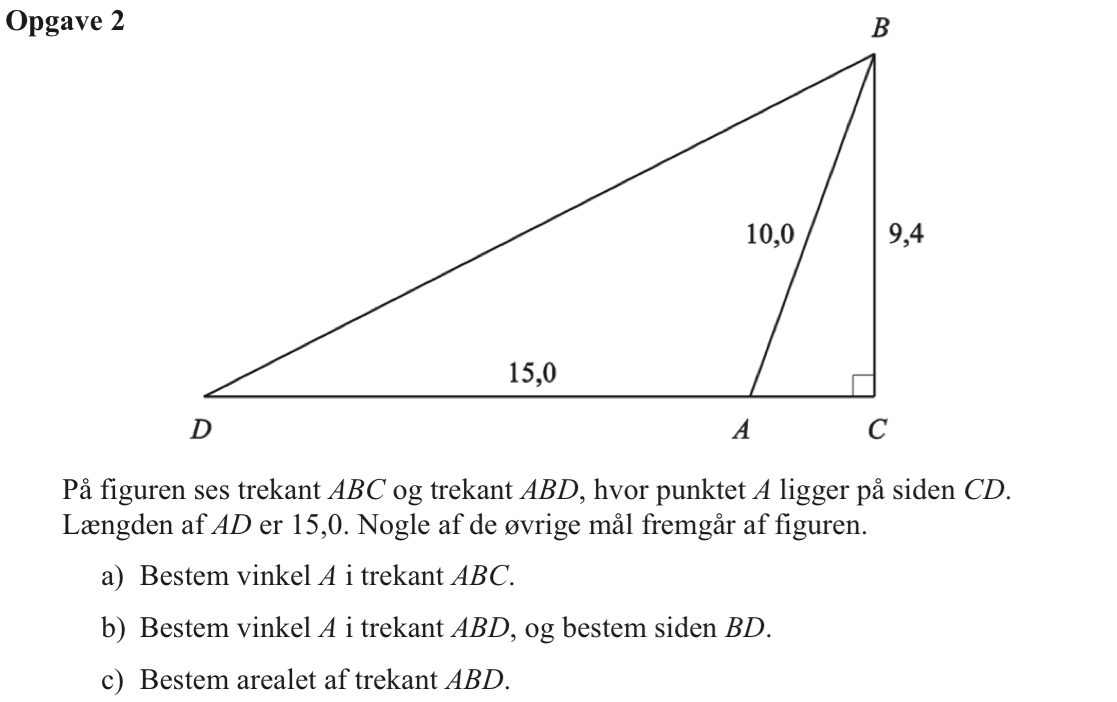
Svar på opgave 2:

1. Vinkel A er vinklen mellem hypotenusen og den ene katete i den retvinklede trekant ABC. Der gælder at:

   10·sin(∠A) = 9,4 ⇒ ∠A = sin^-1(9,4/10,0) ⇒ ∠A = 70,0516° = 70,1°

2. Vinkel A i trekant ABD er supplementvinkel til vinkel A i trekant ABC. Dermed er ∠BAD = 180° - 70,1° = 109,9°

   Man finder |BD| ved hjælp af en cosinusrelation i Ti-Nspire:

   solve(cos(109.9°)=(15²+10²-bd²)/(2*10.*15),bd) ▸ bd=−20.667 or bd=20.667. Her er kun den positive løsning gyldig.

   Dvs. |BD| = 20,7

3. Arealet af trekant ABD er 0,5·grundlinje gange højde = 0,5·15·9,4 = 70,5

Svar på opgave 3:

1. Man skal løse følgende to sammenhørende ligninger med hensyn til a og b: 120 = b·a¹¹ og 10 = b·a²². Man får følgende i Ti-Nspire:

   solve(120.=b*a¹¹ and 10=b*a²²,a,b) ▸ a=0.797797 and b=1440.

   Dvs. a = 0,798 og b = 1440

2. For at finde antallet af minutter, som man må arbejde, indsætter man x = 32 i formlen. Man får: (1440·0,798³²) min. = 1,04 min.

Svar på opgave 4:

1. Man opretter aldrene som en liste i Ti-Nspire:

   alder:={13,25,40,60,80} ▸ {13,25,40,60,80}

   Ligeledes oprettes procenterne som en liste:

   procent:={0,42,32,22,4} ▸ {0,42,32,22,4}

   De kummulerede frekvenser beregnes ud fra procenterne i Ti-Nspire:

   kumm_frekvens:=(cumulativeSum(procent)/100.) ▸ {0.,0.42,0.74,0.96,1.}

   Det giver følgende sumkurve i Ti-Nspire:

   

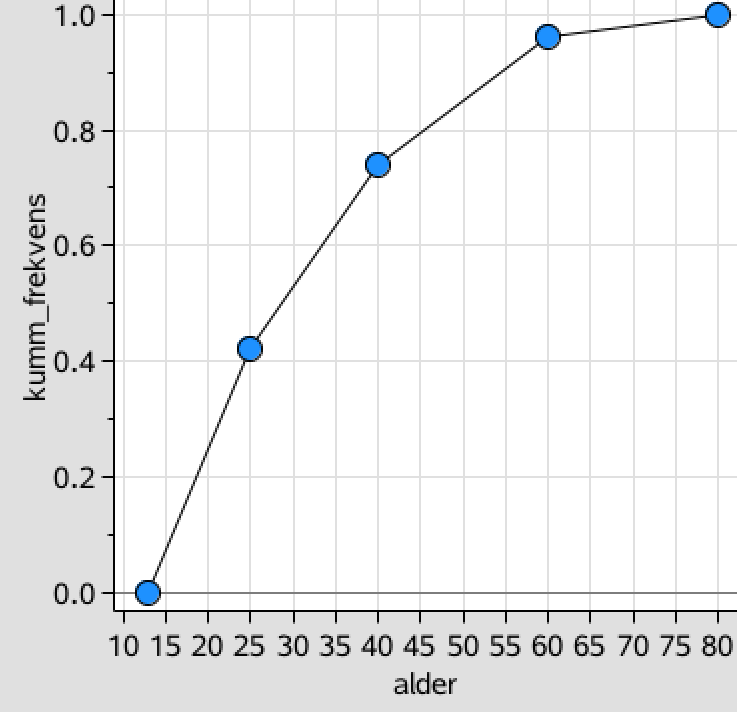
2. For at finde kvartilsættes indsætter man vandrette linjer ud for 0,25; 0,5 og 0,75 i sumkurven.

   

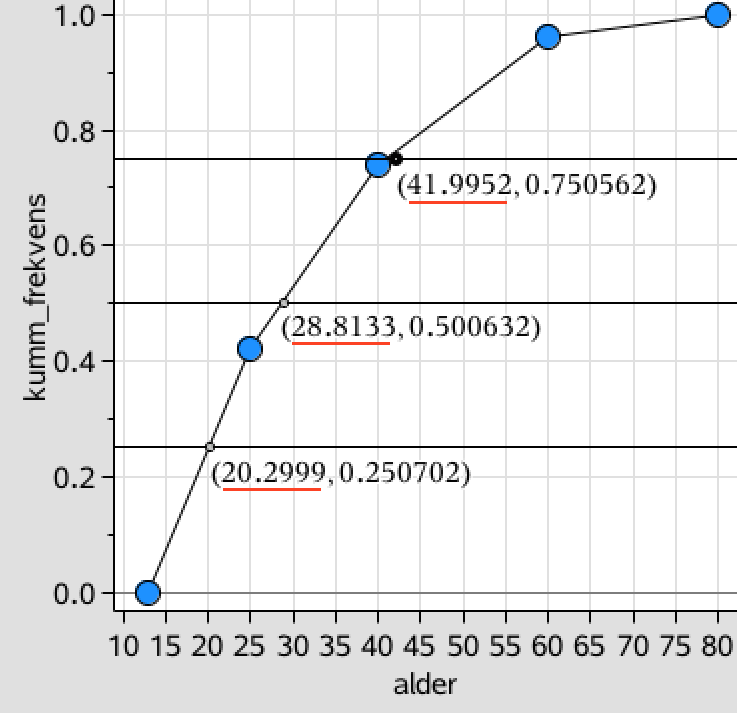
   Det giver kvartilsættet: {nedre kvartil, median, øvre kvartil} = {20,2;28,8;42,0}

   Medianen er den alder, som halvdelen af Facebookbrugerne ligger under.

Svar på opgave 5:

1. Tallet 3,4 er startværdien, dvs. antal mio. indbyggere i 1960. Tallet 1,0225 er fremskrivningsfaktoren, dvs. det tal man skal gange sidste års indbyggertal med for at få dette års indbyggertal.

2. Fordoblingstallet er ln(2)/ln(1,0225) år = 31,2 år.

Svar på opgave 6:

1. Der gælder, at prisen for brød divideret med indekstal for brød for et givet år skal give det samme for alle år.

   Man får defor følgende ligning, hvor x er prisen på brød i 2009: (15 kr.)/117 = x/137 ⇒ x = 17,60 kr.

Svar på opgave 7:

1. Kogetiden for et æg på 57 gram er i følge formlen: 18,2·57^0,67 sek. = 273 sek.

2. Man bruger formlen for procent-procentvækst for en potensfunktion. Det giver: (1,15^0.67-1)·100 % = 9.81649 %

   Dvs. kogetiden er 9,8 % længere for det store æg end for det lille.

Svar på opgave 8:

1. En mand, der vejer 70 kg, får følgende promille efter at have drukket 5 genstande: 12·5/(0,68·70) = 1,26

   Man kalder antallet af genstande for x. Man skal finde det x, som opfylder ligningen: 12·x/(0,68·70) = 0,5. Man får: 12·x/(0,68·70) = 0,5 ⇒ x = 0,5·0,68·70/12 ⇒ x = 1,98.

   Dvs. en mand på 70 kg skal drikke 2 genstande for at nå promillegrænsen.