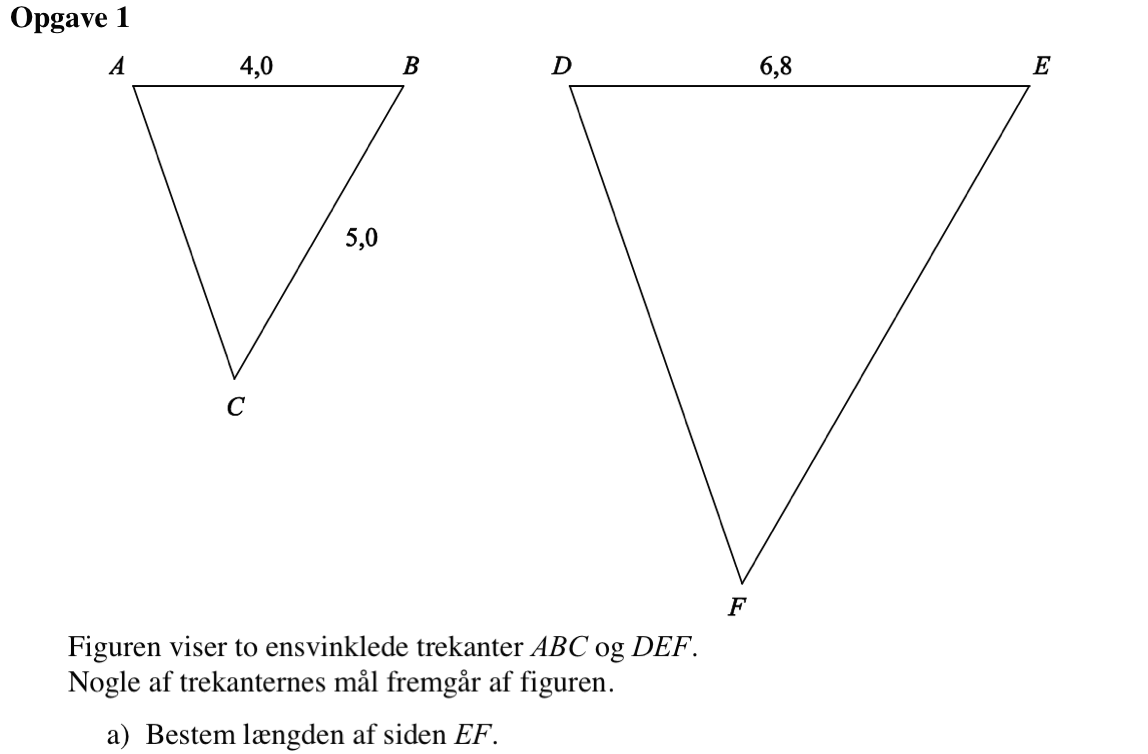
Svar på opgave 1:

1. Der gælder, at |EF|/|BC| = |DE|/|AB| ⇒ |EF| = |BC|·|DE|/|AB| ⇒ |EF| = 5,0·6,8/4,0 ⇒ |EF| = 8,5

Svar på opgave 2:

1. Tallet 300.841 er antallet af Facebook brugere i 2007, det år hvor x = 0.

   Tallet 1,147 er fremskrivningfaktoren, dvs. det tal som skal gange det gamle års antal brugere med for at få det nye års.

2. Man skal løse ligningen 300841·1,147^x = 1000000 med hensyn til x. Dette gøre i Ti-Nspire:

   y(x):=300841*(1.147)^x ▸ Udført (oprettelse af funktion)

   solve(y(x)=1000000,x) ▸ x=8.75811

   Dvs. der går 8,8 måneder før antallet af Facebookbrugere er oppe på 1000000.

3. Antallet af Facebookbrugere efter 22 måneder er 300841·1,147²² = 6,15 mio.

   Dvs. der er 6,15 millioner beregnede brugere. Det er ca. tre gange flere end i virkeligheden.

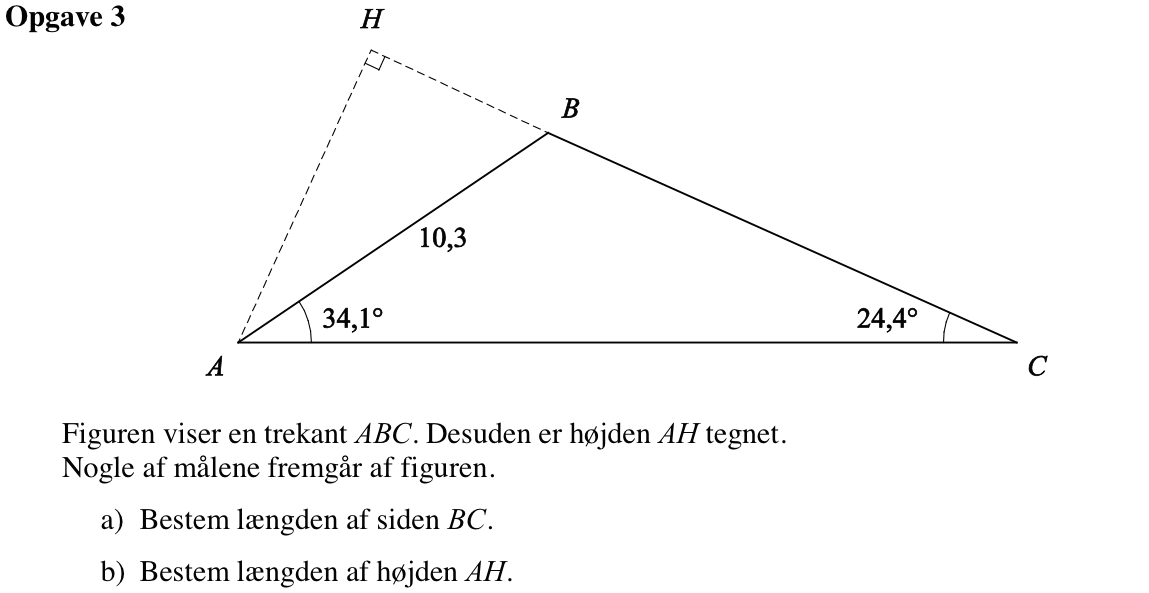
Svar på opgave 3:

1. |BC| findes ved hjælp af en sinusrelation: |BC|/sin(31,4°) = 10,3/sin(24.4°) ⇒ |BC| = sin(31,4°)·10,3/sin(24.4°) ⇒ |BC| = 13,0

2. Man starter med at beregne ∠ABH. Supplementvinklen ∠ABC = 180° - (34,1° + 24,4°). Dette giver: ∠ABH = 180° - ∠ABC = 180° - [180° - (34,1° + 24,4°)] = 34,1° + 24,4° = 58,5°. Dette er vist på nedenstående figur:

   

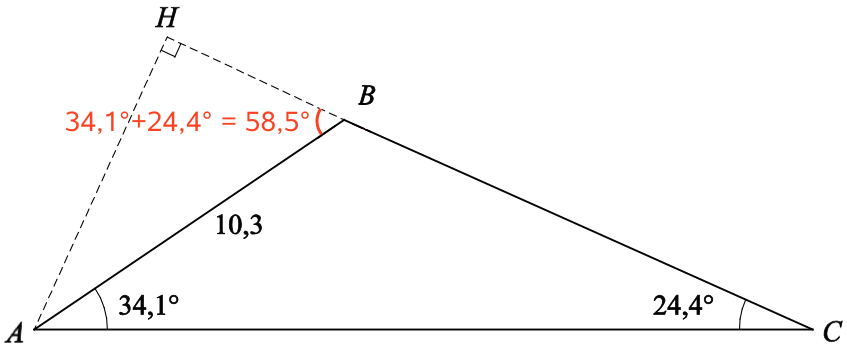
   Da trekant ABH er retvinklet med AB som hypotenuse, får man: |AH| = 10,3·sin(58,5°) = 8,78

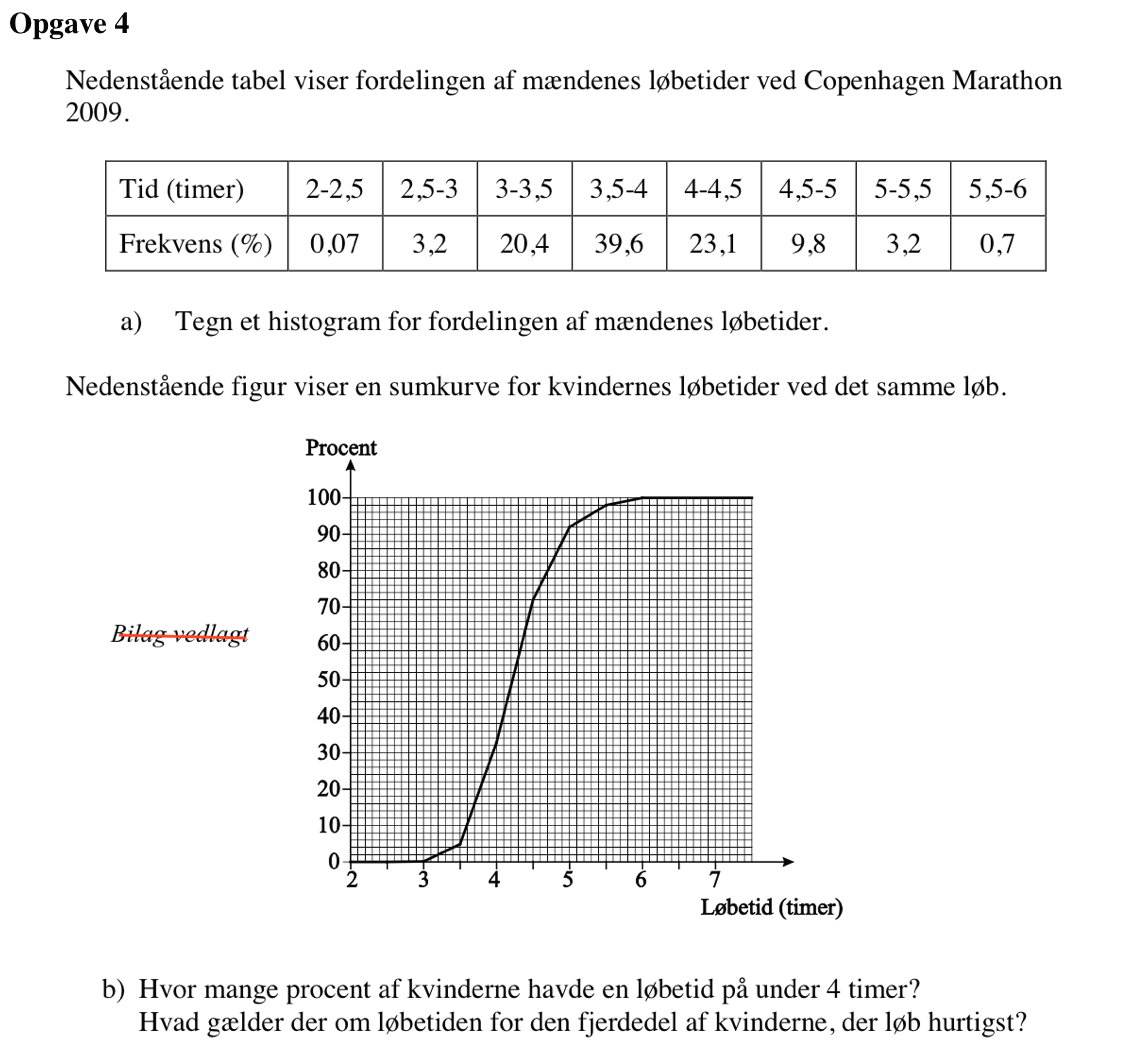
Svar på opgave 4:

1. Man opretter en liste med de nedre grænser til tidsintervallerne i Ti-Nspire:

   tid:={2,2.5,3,3.5,4,4.5,5,5.5} ▸ {2,2.5,3,3.5,4,4.5,5,5.5}

   Man opretter ligeledes en liste med frekvenserne:

   frekvens:={0.07,3.2,20.4,39.6,23.1,9.8,3.2,0.7} ▸ {0.07,3.2,20.4,39.6,23.1,9.8,3.2,0.7}

   Ud fra disse lister laves nedenstående histogram:

   

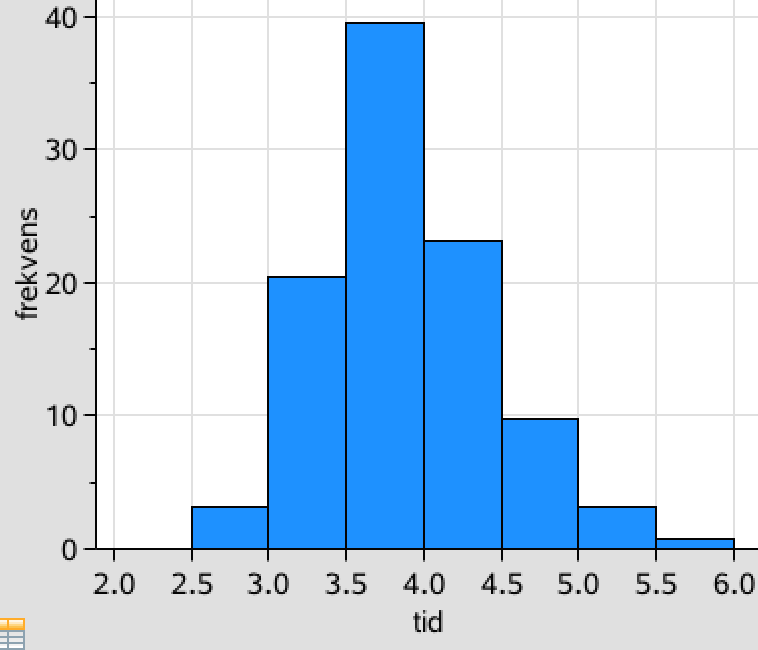
2. Den grønne pil på nedenstående figur viser, hvordan man finder den andel af kvinderne, der havde en løbstid på under 4 timer.

   Den røde pil viser hvordan man aflæser løbstiden for den fjerdedel af kvinderne, der løb hurtigst.

   

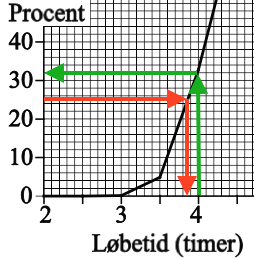
   Andelen af kvinder der løb på under fire timer aflæses til 32 %

   Tiden, som den bedste fjerdedel af kvinderne var under, aflæses til 3,85 timer = 3 timer og 51 min.

Svar på opgave 5:

1. Man skal løse følgende to sammenhørende ligninger med hensuyn til a og b: 2 = b·1^a og 16 = b·4^a. Dete gøres i Ti-Nspire: solve(2=b*1^a and 16.=b*4^a,a,b) ▸ a=1.5 and b=2.

   Dvs. a = 1,5 og b = 2

2. Når x = 2,25 er y = 2·2,25^1,5 = 6,75

   For finde det x som giver y = 31,25 skal man løse ligningen 2·x^1,5 = 31,25. Dette gøres i Ti-Nspire: solve(2.*x^1,5=31.25,x) ▸ x=6.25

   Dvs. det x, som giver y =31,25 er 6,25

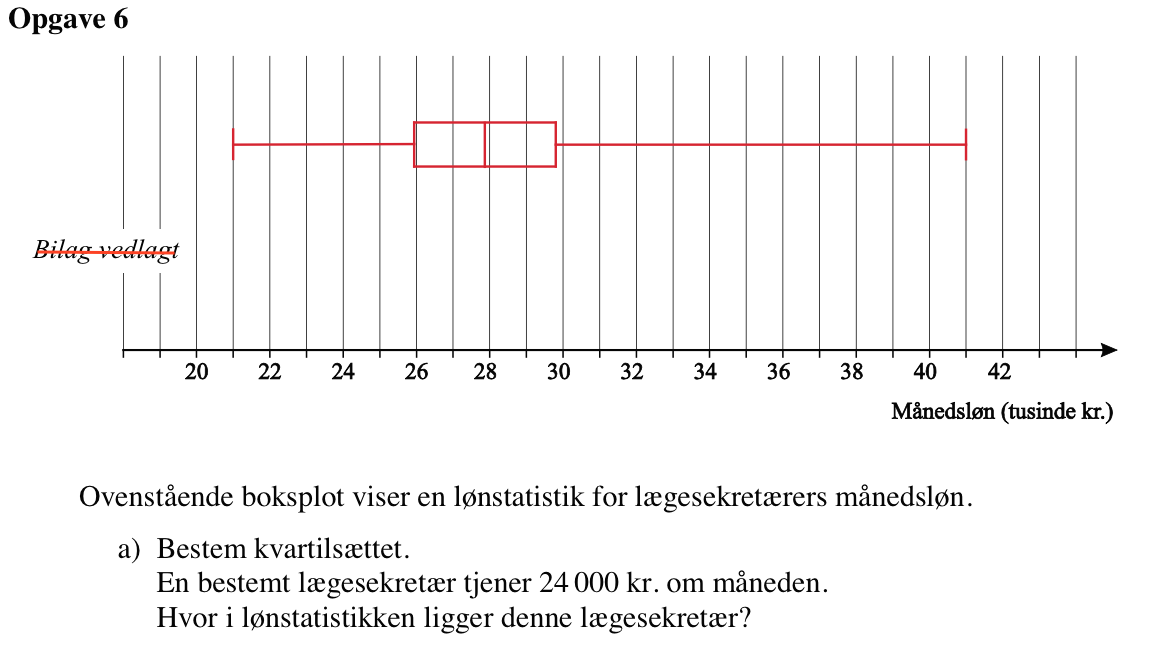
Svar på opgave 6:

1. Kvartilsættet aflæses til {nedre kvartil, median,øvre kvartil} = {25900,27800,29700}

2. Sekretæren ligger under nedre kvartil og er derfor blandt de 25 % lavest lønnede lægesekretærer.

Svar på opgave 7:

1. Mængden af saltvand, der er tilbage er 950 mL - (5 mL/min.)·(45 min.) = 725 mL

   Forskriften er f(x) = -5x + 950, hvor f(x) er mængden af tilbageværende saltvand og x er tiden i minutter.

2. Man skal løse ligningen 950 mL - (5 ml/min.)·x = 250 mL ⇒ x = 140 min.

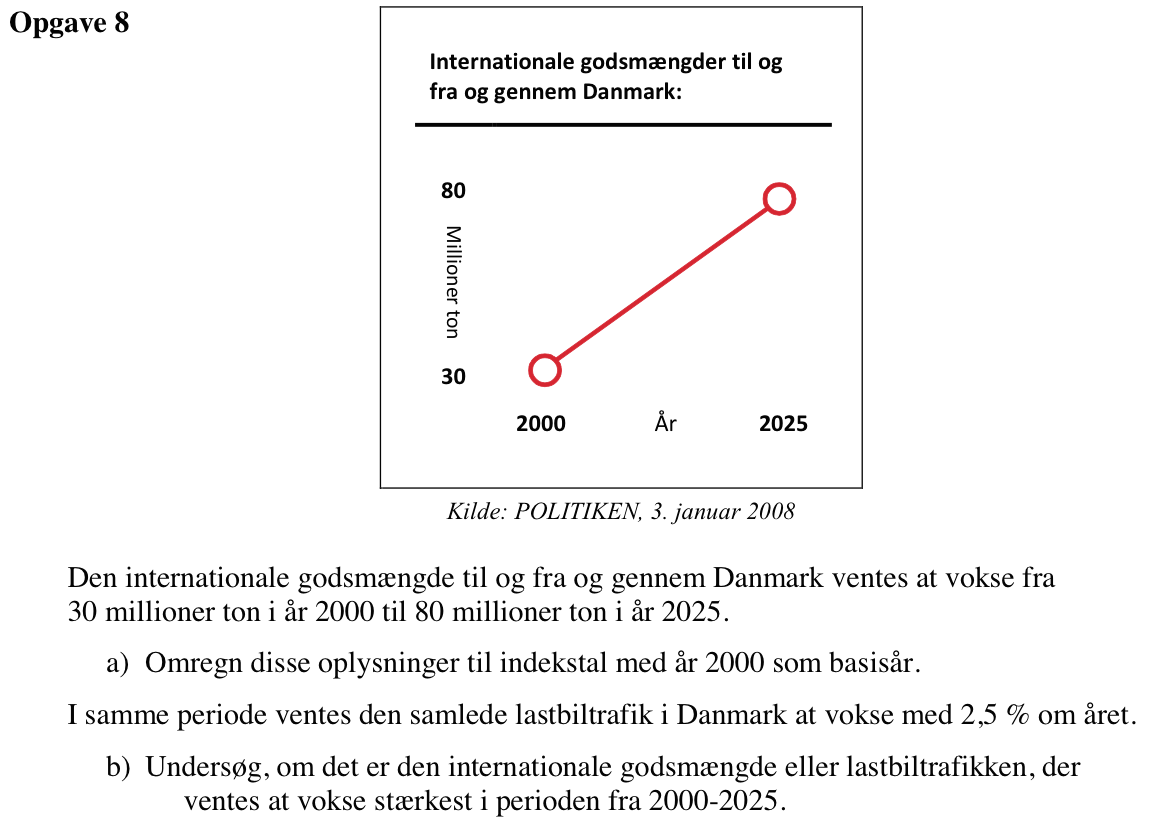
Svar på opgave 8:

1. Godsmængde for 2000 divideret med indeks for 2000 er lig med godsmængde for 2025 divideret med indeks for 2025. Det giver:

   Indeks for 2025 = 100·80/30 = 266,7

2. Lastbiltrafikken vokser med (1+(2.5)%)²⁵ = 1,854. Dvs. indeks for lastbiltrafikken vokser fra 100 i 2000 til 100·1,854 = 185 i 2025.

   Dermed vokser godsmængden mere end lastbiltrafikken.