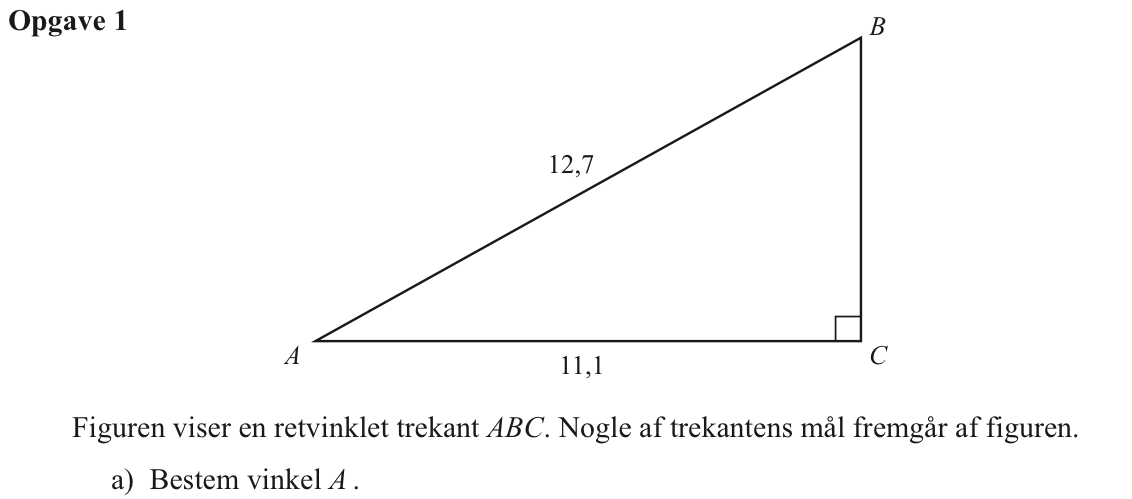
Svar på opgave 1:

1. Man benytter, at i den retvinklede trekant ABC, er |BC| = |AC|·cos(∠A) ⇒ 11,1 = 12,7·cos(∠A) ⇔ cos(∠A) = 11,1/12,7 ⇒ ∠A = cos^-1(11,1/12,7) = 29,1°

Svar på opgave 2:

1. Modellen er f(x) = 2795x + 17500, hvor f(x) er leasingudgifterne og x antal måneder, som bilen er leaset.

2. Man skal løse ligningen: 2795x + 17500 = 139000 ⇔ x = 43,5. Dvs. der går 43,5 mdr. før leasingudgifterne overstiger 139000 kr.

Svar på opgave 3:

1. For at finde højden af keglen skal man løse ligningen 150 = (1/3)·π·4²·h med hensyn til h:

   150 = (1/3)·π·4²·h ⇔ h = 150/[(1/3)·π·4²] = 8,95. Dvs. højden er 9,0 cm

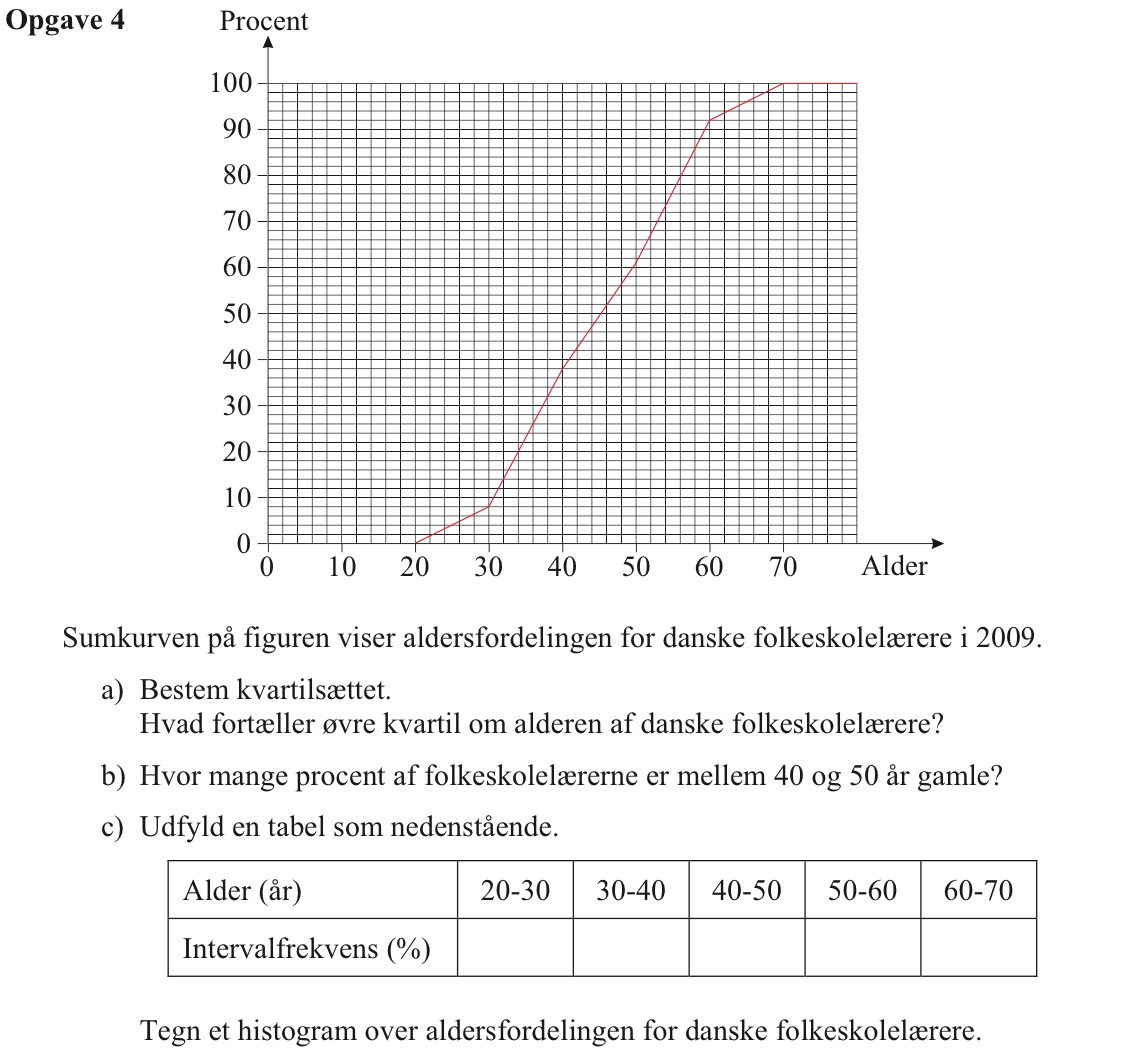
Svar på opgave 4:

1. Kvartilsættes findes som vist på figuren nedenunder:

   

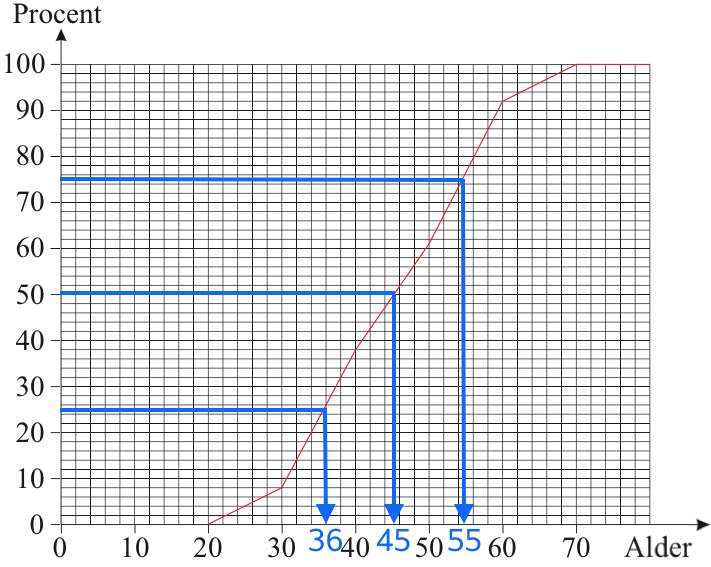
   For hver af tallene 25 %, 50 % og 75 % på anden-aksen finder man den tilsvarende værdi på førsteaksen. Disse tal giver: nedre kvartil = 36 år, median = 45 år og øvre kvartil = 55 år

2. Af figuren nedenunder aflæser man at andelen af lærere, som er under 40 år er 38 % og at andelen af lærere, som er under 50 år er 61 %. Andelen af lærere, som er mellem 40 og 50 år er andelen af lærere, som er under 50 år fratrukket andelsen som er under 40 år.

   

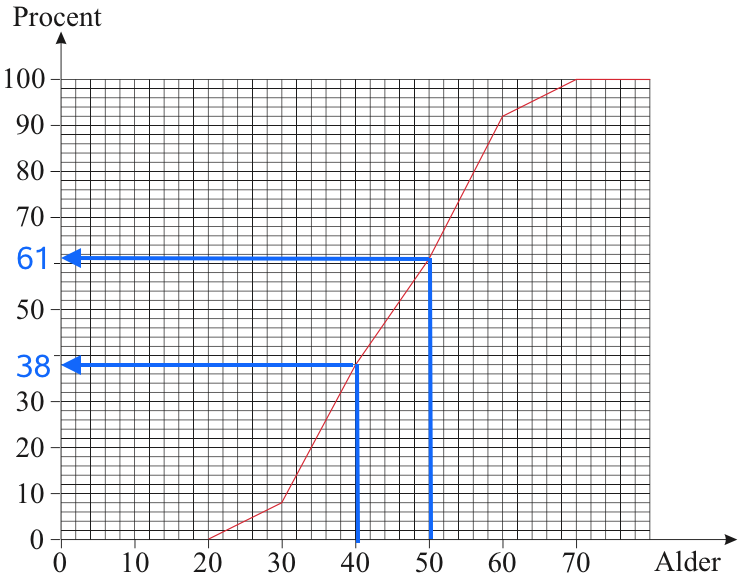
   Dette giver, at andelen af lærere, som er mellem 40 år og 50 år er 61 % - 38 % = 23 %

3. Intervalfrekvenserne kan udregnes fra sumkurven som vist nedenunder.

   

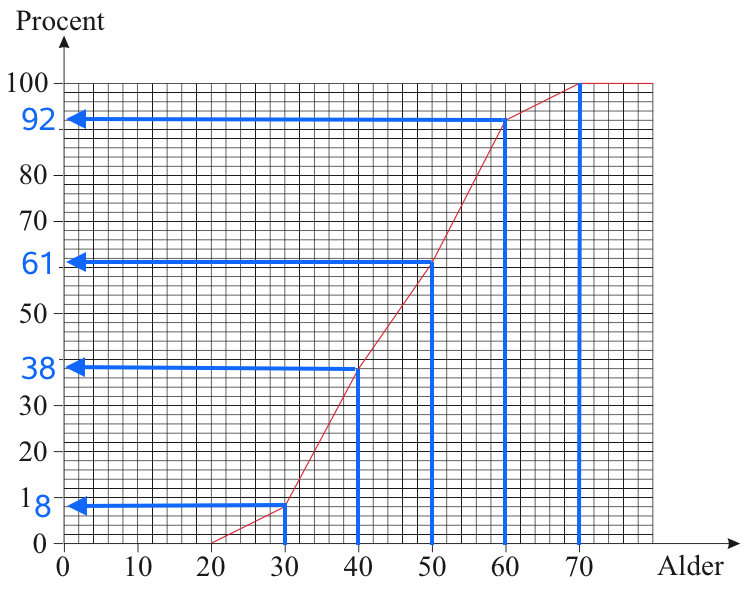
   Man får frekvenserne:

   ]20;30]: (8 - 0) % = 8 %

   ]30;40]: (38 - 8) % = 30 %

   ]40;50]: (61 - 38) % = 23 %

   ]50;60]: (92 - 61) % = 31 %

   ]60;70]: (100 - 92) % = 8 %

   Histogrammet kan laves ud fra disse intervalfrekvenser, men det kan også laves grafisk som vist på de to figurer nedenunder.

   På den første figur tegnes blå rektangler, der på den vandrette led går fra det ene intervalendepunkt til det næste. Hvert retangels nedre venstre hjørne ligger på sumkurven og det samme gælder øvre højre hjørne.

   

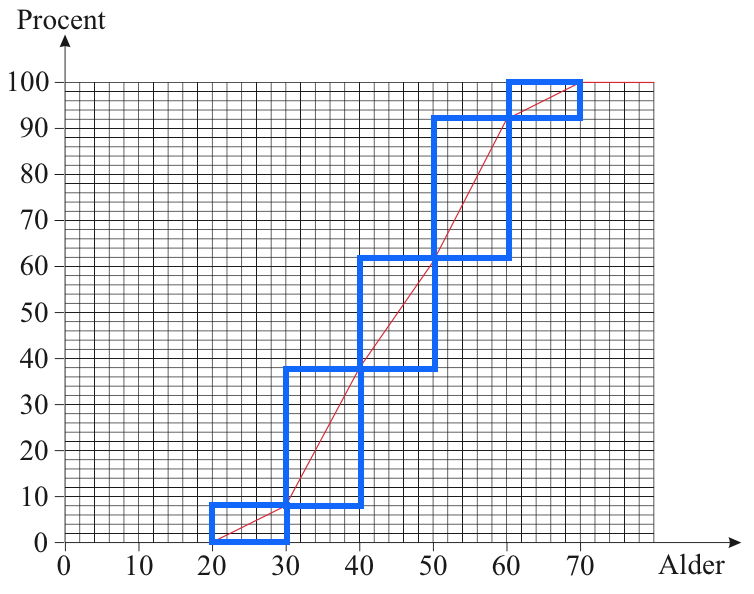
   Når disse rektangler er tegnet på sumkurven, flyttes de de ned til den vandrette akse som vist nedenunder, og man har histogrammet.

   

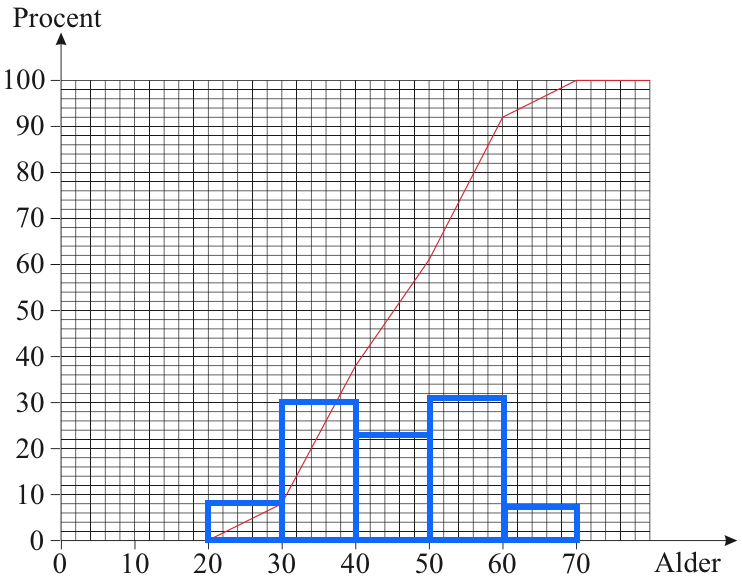
Svar på opgave 5:

1. Mængden af foder for en hund på 40 kg findes ved at indsætte x = 40 i formlen. Man får: 25·40^0,75 = 397,6.

   Dvs. den anbefalede mængde af foder er 398 g

2. Man benytter formlen for procent-procentvækst for en potensfunktion: (1,30^0,75 - 1)·100 % = 21,75 %.

   Dvs. den tunge hund skal have 22 % mere foder end den lette.

Svar på opgave 6:

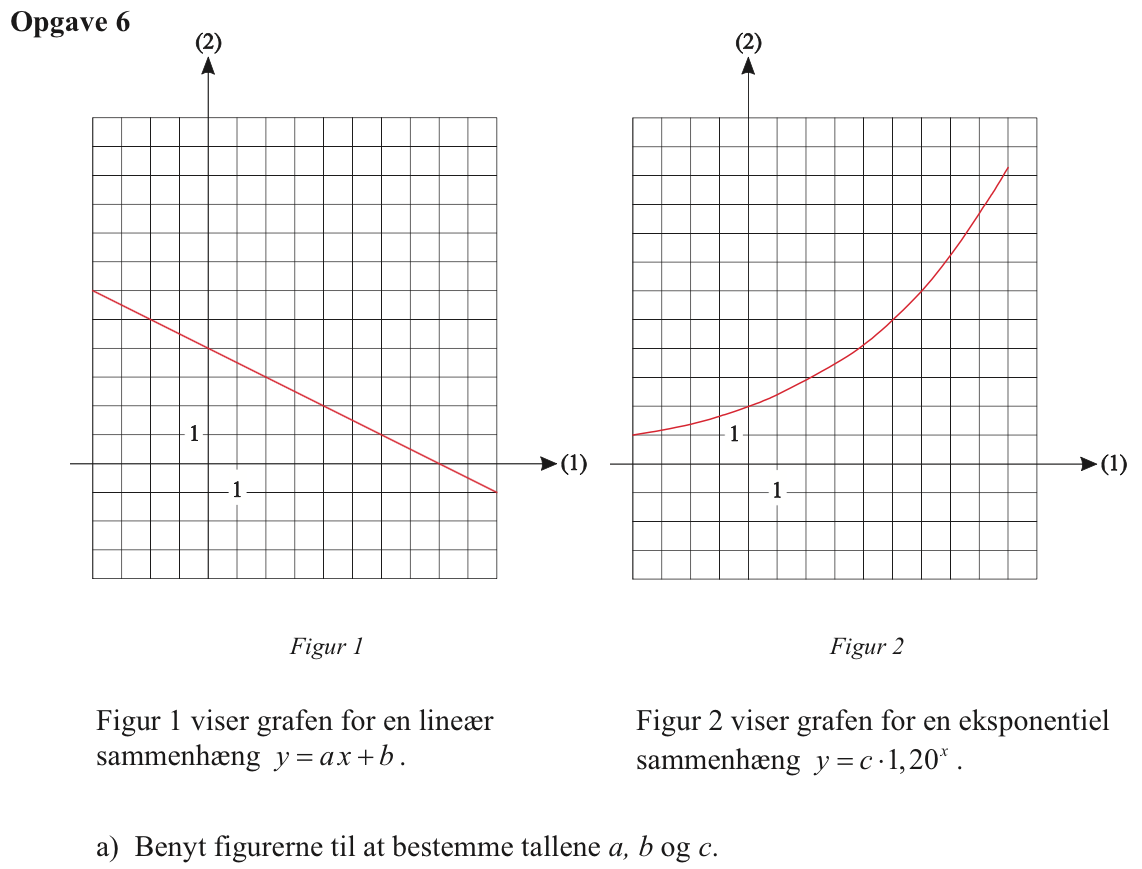
1. Konstanten b aflæses som grafens skæring med anden aksen på figur 1. Den aflæses til b = 4. (Indses ved at sætte x = 0 i y = ax + b.)

   På samme måde aflæses c som skæringen med andenaksen på figur 2. Dvs. c = 2. (Indses ved at sætte x = 0 i y = c·1,20^x.)

   Konstanten a findes som hældningen af kurven på figur 1. Den er: a = -4/8 = -1/2

Svar på opgave 7:

1. Man skal løse de to sammenhørende ligninger: 4714 = b·a⁰ og 6552 = b·a⁸. Dette gøres i Ti-Nspire: solve(4714=b*a⁰ and 6552.=b*a⁸ and a>0,a,b) ▸ a=1.04201 and b=4714..

   Dvs. a = 1,042 og b = 4714

2. Fordoblingskonstanten er ln(2)/ln(1,042) = 16,85, dvs. antallet af influenza-tilfælde fordobles hver 17. dag.

3. Man skal løse ligningen 4714·1,042^x = 21000 med hensyn til x. Man får følgende i Ti-Nspire: solve(4714.*(1.04201)^x=21000,x) ▸ x=36.3045

   Man runder op og får at 21000 influenza-tilfælde passeres efter 37 dage

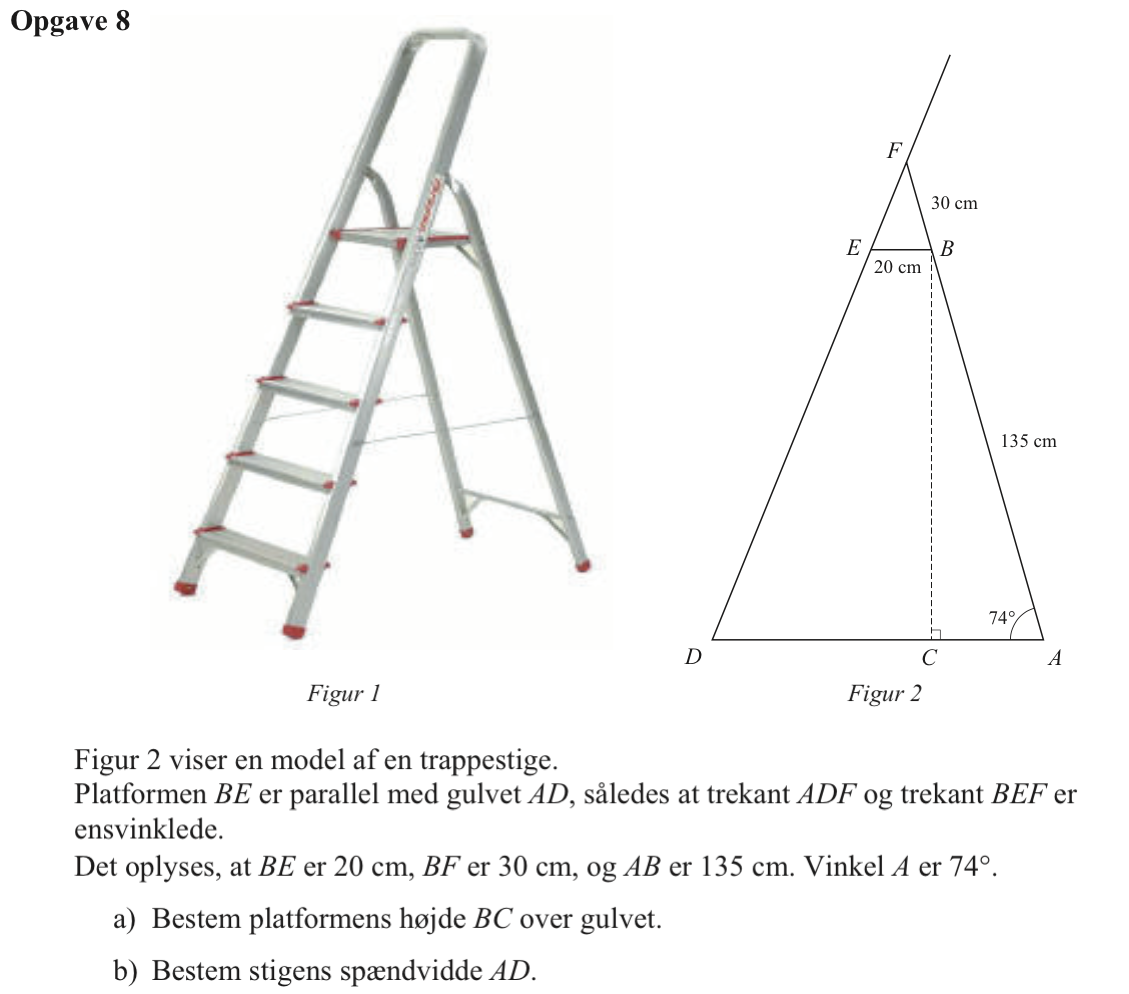
Svar på opgave 8:

1. Trekant ABC er retvinklet og man får at: |BC| = |AB|·sin(∠A) ⇒ |BC| = 135·sin(74°) = 129,8. Dvs. platformens højde over gulvet er 130 cm

2. Trekant BEF og trekant ADF er ensvinklede. Der gælder at |EB|/|FB| = |AD|/|AF| ⇒ 20/30 = |AD|/(135+30) ⇒ |AD| = 110. Dvs. at stigens spændvidde er 110 cm