Svar på opgave 1:

1. Man skal bruge kapitalformlen: K = K₀·(1 + r)ⁿ. Her skal man finde K. K₀ = 10.000, r = 2,5 % (= 0,025) og n = 6. Dette gver:

   K = 10.000·(1 + 2,5 %)⁶ = 10.000·1,025⁶ = 11.596,90.

   Dvs. beløbet på kontoen efter 6 år er 11.597 kr.

2. Man skal igen bruge kapitalformlen. Her skal man finde n, så K = 2·K₀ = 20.000 og r = 0,025. Dette gver:

   20.000 = 10.000·1,025ⁿ ⇔

   2 = 1,025ⁿ ⇔

   ln(2) = ln(1,025ⁿ) ⇔

   ln(2) = n·ln(1,02) ⇔

   ln(2)/ln(1,02) = n ⇔

   n = 35,00

   Dvs. beløbet på kontoen fordobles efter 35 år

Svar på opgave 2:

1. På figuren nedenunder er indtegnet trigonometriske formler til løsning af opgaverne:

   

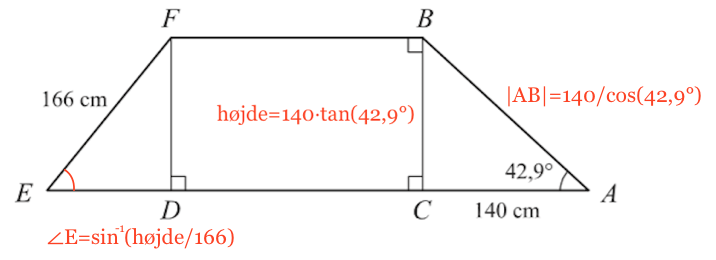
   Trekant ABC er retvinklet. Der gælder derfor, at |BC|/|AC| = tan(∠A). Idet teltets højde = |BC|, |AC| = 140 og ∠A = 42,9° får man:

   højde/140 = tan(42,9°) ⇔ højde = 140·tan(42,9°) ⇔ højde = 130,096.

   Dvs. teltets højde er 130 cm

   |AB| kan herefter enten findes ved hjælp af trigonometri eller ved hjælp af Pythagoras læresætning.

   Hvis man bruger trigonometri, får man den formel, som er vist til højre på ovenstående figur. Dette udledes på følgende måde:

   |AB|·cos(∠A) = |AC| ⇒ |AB| = |AC|/cos(∠A) ⇒ |AB| = 140/cos(42,9°) ⇒ |AB| = 191,1.

   Ved at bruge Pythagoras læresætning får man: |AB|² = |AC|² + |BC|² ⇒

   |AB|² = 140² + 130,1² ⇔ |AB|² = 36526,01 ⇒

   |AB| = √[36526,01] ⇔ |AB| = 191,1

   Dvs. |AB| = 191 cm

2. For vinklen E gælder, at |EF|·sin(∠E) = |DF| ⇒ |EF|·sin(∠E) = |BC| ⇒ 166·sin(∠E) = 130,1 ⇒

   sin(∠E) = 130,1/166 ⇒ ∠E = sin^-1(130,1/166) ⇔ ∠E = 51,6°

   Dvs. vinkel E = 51,6°

Svar på opgave 3:

1. Mennesker med en indkomst over 1 million kr. om året er i det følgende kaldet millionærer.

   Der er tale om en årlig vækst med et fast antal og dermed om lineær positiv vækst.

   Denne model har formlen: y = a·x + b, hvor y er antallet af danske millionærer og x er antal år efter 2000.

   Tallet a er den årlige vækst i antal og denne ved man er 1300.

   For x = 0 (år 2000) er y = b. Der 7600 danske millionærer i 2000, og dermed er b = 7600.

   Dvs. modellen bliver y = 1300·x + b, x> 0

2. Antal millinærer i 2009 er ifølge modellen: 1300·9 + 7600 = 19.300

   I det andet spørgsmål skal man først løse ligningen 1300·x + 7600 = 23000 med hensyn til x. Dette giver:

   1300·x + 7600 = 23000 ⇔ 1300·x = 23000 - 7600 ⇔

   x = (23000 - 7600)/1300 ⇔ x = 11,8

   Dette tal lægges til 2000 og man runder op til nærmeste hele årstal: 2000 + 12 = 2012

   Dvs. det år, hvor der hele hele året er mere end 23000 millionærer i Danmark er 2012

Svar på opgave 4:

1. Man sætter indeks for basisåret 1996 til 100. Indekset for 2006 kaldes x som vist i tabellen nedenunder:

   

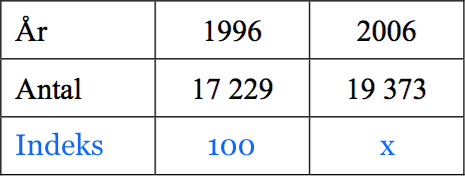
   Der gælder at: 17229/100 = 19373/x ⇔ x = 19373/(17229/100) = 100·(19373/17229) = 112,4

   Dvs. indekstallet for antallet af pædagogstuderende i 2006 er 112

Svar på opgave 5:

1. Man skal løse to ligninger med to ubekendte for at finde a og b. Man indsætter tallene fra tabellen i ligningerne:

   35.359 = b·a⁰ ∧ 50.118 = b·a⁴ ⇔

   35.359 = b ∧ 50.118 = 35.359·a⁴ ⇔

   b = 35.359 ∧ ⁴√[50.118/35.359] = ⁴√[a⁴] ⇔

   b = 35.359 ∧ a = 1,0911

   Dvs. a = 1,0911 og b = 35.359

2. 2007 svarer til x = 6. Ved at indsætte x = 6 i modellen y = 35.359·1,0911⁶ = 59.660,56

   Dette viser at modellen viser for lidt.

Svar på opgave 6:

1. Man har formlen T(x) = 0,28·x^1,5 og skal finde tallet T(0,5). Man får:

   T(0,5) = 0,28·0,5^1,5 = 0,098995

   Dvs. svingningstiden for en bladfjeder med længden 0,5 m er 0,099 s

2. Man skal bruge formlen for procent-procentvækst for en potensfunktion. Fremskrivningsfaktoren er 1,20. Man får:

   Procentvækst for T(x) er: ((1,20)^1,5 - 1)·100 % = 31,45 %.

   Dvs. svingningstiden øges med 35 %, når bladfjederen længde øges med 20 %.

Svar på opgave 7:

1. Nedenunder er boksplottet for person nr. 1 vist med blå farve.

   

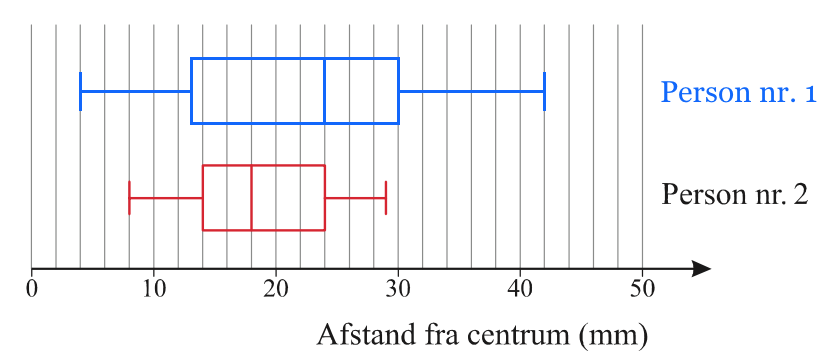
   Det ses, at medianen (stregen inde i firkanten) for person nr. 1 er større end for person nr.2. Dvs. at person generelt rammer dårligere end person nr. 2. Samtidig er variationsbredden (bredden af hele plottet) mindre for person nr. 2. Det viser at person nr. 2 rammer mere ens end person nr. 1.

Svar på opgave 8:

1. Sammenhængen kan skrives: I(x) = 21462/x². Man skal finde I(20). Dette giver:

   I(20) = 21462/20² = 53,655

   Dvs. lysstyrken er 53,7 μW/m² i en afstand af 20 m fra lygten.

    

   For at finde afstanden skal man løse lignigen I(x) = 95 med hensyn til x. Man får:

   I(x) = 95 ⇒ 21462/x² = 95 ⇔

   x² = 21462/95 ⇒ (kun positive værdier af x er gyldige, da det er en afstand)

   x = √[21462/95] = 15,0305

   Dvs. afstanden fra lygten, hvor lysstyrken er 95 μW/m² er 15,0 m

Svar på opgave 9:

1. Man finder middeltallet (for grupperede data) ved at gange midten af hvert interval med frekvensen for det enkelte interval og lægge produkterne sammen:

   Middeltal = [(40 + 60)/2]·8 % + [(60 + 80)/2]·18 % + [(80 + 100)/2]·39 % + [(100 + 120)/2]·30 % + [(120 + 140)/2]·5% =

   50·0,08 + 70·0,18 + 90·0,39 + 110·0,30 + 130·0,05 = 91,2