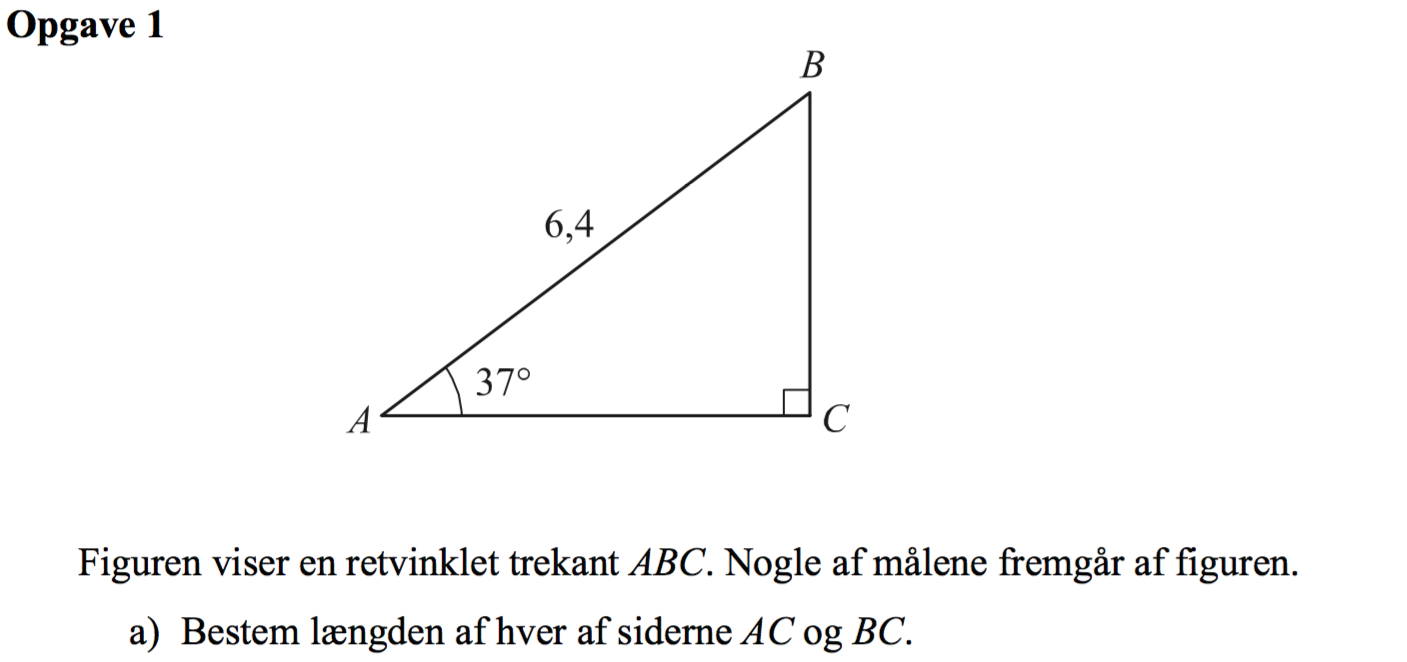
Svar på opgave 1:

1. |AC| = 6,4·cos(37°) = 5,111

   |BC| = 6,4·sin(37°) = 3,852

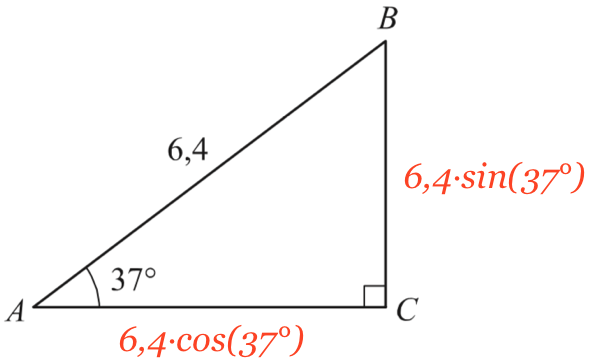
   Formlerne er vist på nedenstående tegning:

   

Svar på opgave 2:

1. Man bruger kapitalformlen for at finde det indsatte beløb: K = K₀·(1 + r)ⁿ. Her skal man finde K₀. K = 8.826,65 kr., r = 2,75 % = 0,0275 og n = 7. Dette giver:

   K = K₀·(1 + r)ⁿ ⇒ 8.826,65 = K₀·(1 + 0,0275)⁷ ⇔ 8.826,65 = K₀·(1,0275)⁷ ⇔

   K₀ = 8.826,65/1,0275⁷ = 8.826,65/1,2091 = 7.300

   Dvs. det indsatte beløb var 7.300 kr.

Svar på opgave 3:

1. Der er tale om en negativ lineær model (eller udvikling), idet der dels sker et fald, dels er faldet en konstant mængde eller konstant antal pr tidsenhed. (Et konstant procentvist fald pr. tidsenhed ville have betydet en aftagende eksponentiel udvikling).

   Modellen er: f(t) = 165.200 - 2.900·t,

   hvor t (0 ≥ t ≥ 20) er tiden i måneder fra og med april 2005 og f(t) er antallet af ledige en given måned.

Svar på opgave 4:

1. Tallet 15 er startmængden af amfetamin målt i mg. (Indses ved at sætte x = 0).

   Tallet 0,84 er fremskrivningsfaktoren for mængden af amfetamin, dvs. det tal, som man skal gange den gamle mængde med for at finde den nye for hver time.

2. Mængden af amfetamin i kroppen efter 2,0 timer er 15·0,84^2,0 mg. = 10,6 mg.

   Formlen for halveringstiden (T) er: T = ln(0,5)/ln(a) = ln(0,5)/ln(0,84) timer = 3,98 timer

Svar på opgave 5:

1. Løsning i Ti-Nspire:

   Man opretter en liste med aldersgrænser (kaldet alder_år). Man indsætter 79 som øvre grænse for sidste inteval(en højere alder kan også vælges).

   alder_år:={18,29,39,49,59,69,79} ▸ {18,29,39,49,59,69,79}

   Man opretter en liste med frekvenser for andelsen af personer under eller lig med en given grænse og ældre end den foregående:

   frekvens:={0,(19.)%,(22.)%,(31.)%,(18.)%,(8.)%,(2.)%} ▸ {0,0.19,0.22,0.31,0.18,0.08,0.02}

   (Dvs. 0 % af danske motorcykelejere er under 18 år, 19 % er ældre end 18 og yngre eller lig med 29 osv.)

   Man laver en liste kaldet kumm_frekvens over kummulerede frekvenser fra listen frekvens:

   kumm_frekvens:=cumulativeSum(frekvens) ▸ {0,0.19,0.41,0.72,0.9,0.98,1.}

   Ud fra listerne alder_år og kumm_frekvens laver man en sumkurve:

   

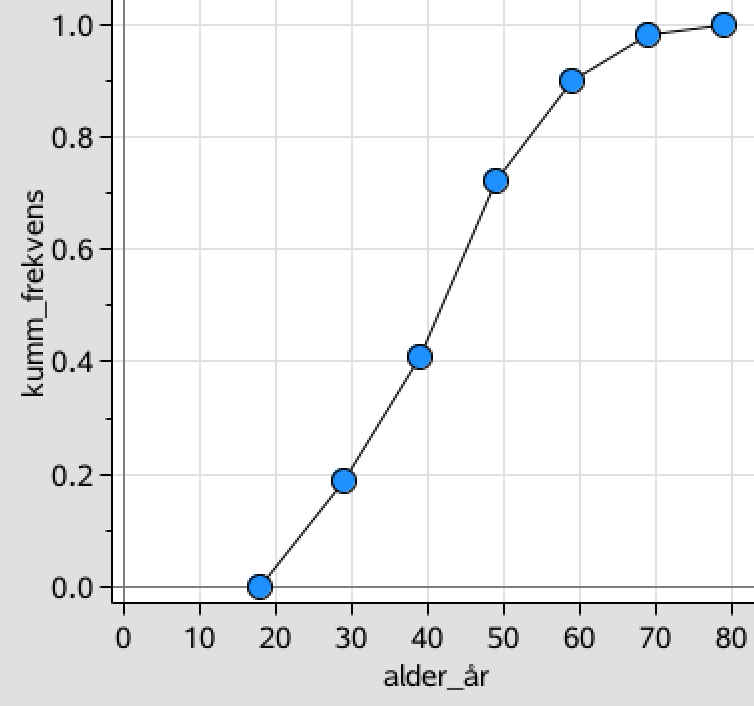
2. På ovenstående sumkurve indsætter man funktionerne f(x) = 0,25, f(x) = 0,5 og f(x) = 0,75. Det giver tre vandrette linjer. Ved hjælp af grafsporingsværktøjet finder man linjernes skæringer med sumkurven. Skæringspunkterner er (31,6;0,25), (42,0;0,5) og (50,7;0,75).

   

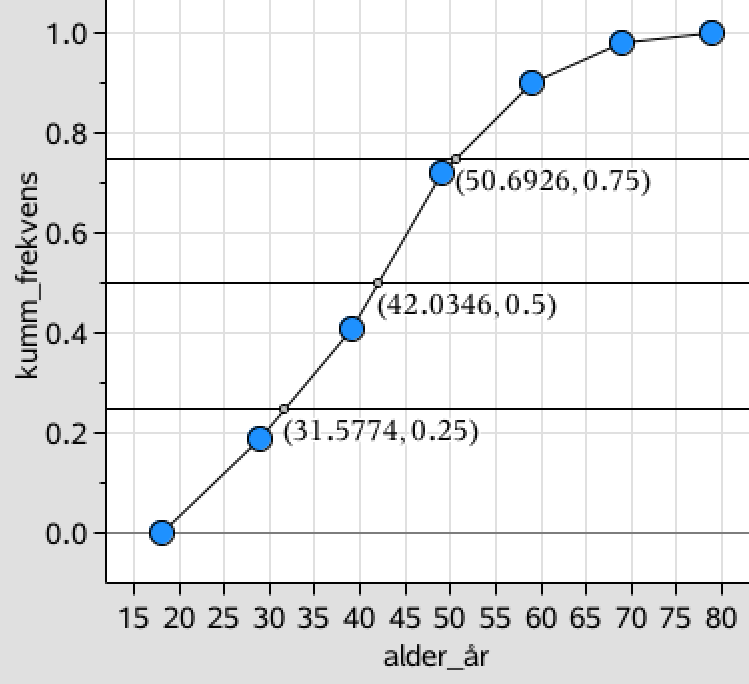
   Dvs. kvartilsættet er: {nedre kvartil; median; øvre kvartil} = {31,6; 42,0 og 50,7}.

   Nedre kvartil er den alder, som 25 % af de danske motorcykelejere har eller er under.

Svar på opgave 6:

1. Man skal finde vægten, y for x = 30. y = 0,00769·30^3,10 = 291,74.

   Dvs. vægten af en ørred på 30 cm er 291,7 g

2. Man skal finde x, når y = 500, dvs. løse ligningen 0,00769·x^3,10 = 500 med hensyn til x. Dette giver i Ti-Nspire:

   solve(0.00769*x^(3.1)=500,x) ▸ x=35.694

   Dvs. længden af en ørred på 500 g er 35,7 cm

3. For en vækst på 15 % er fremskrivningsfaktoren 1,15. Den procentuelle vækst for potensfunktionen er dermed:

   (1,15^3,10 - 1)·100 % = 54,23 %

   Dvs. ørredens vægt vokser med 54,2 %

Svar på opgave 7:

1. Trekant ABH er retvinklet. Dermed gælder, at tan(∠A) = |BH|/|AH| = 21/6,5 = 3.23077.

   Dermed er ∠A = tan^-1(3.23077) = 72,8°

2. Man forlænger siderne AB og DC, så de mødes i punktet T. Derved fremkommer en trekant BTC. Man skal finde højden |TS|.

   

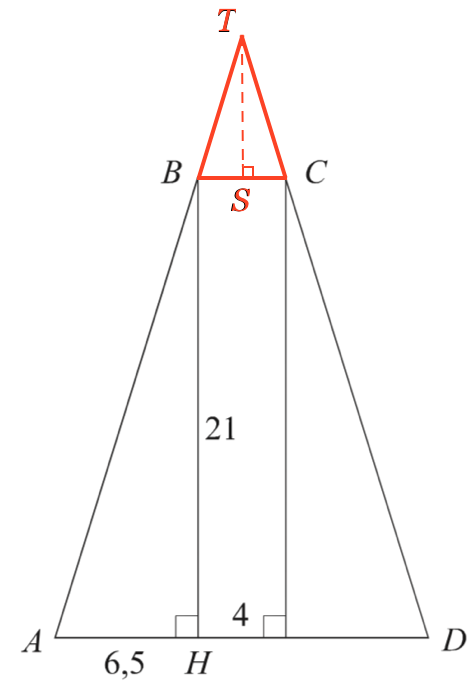
   På grund af parvis parallelitet mellem siderne i trekant ATD og trekant BTC er de ligedannede. Da vinklerne A og D er lige store er vinkel TBC og vinkel TCB det også. Dermed er trekant BTC ligebenet, og således halverer højden TS grundlinjen CB. Dvs. |BS| = 2.

   Man har nu: tan(72,8°) = |TS|/2 ⇒ |TS| = 2·tan(72,8°) = 6.46096.

   Dvs. hvis taget var spidst, ville det være 6,5 m højere.

Svar på opgave 8:

1. Tallet b er startværdien dvs. gennemsnitslevealderen i år 2005, dvs. b = 78,0.

   Tallet s er den gennemsnitlige stigning pr. år dvs: (80,3 - 78,0)/(2005 - 1995) = 2,3/10 = 0,23.

   Dvs. a = 0,23 og b = 78,0

2. Man skal løse ligningen 0,23·x + 78,0 = 81,5 med hensyn til x og finde det hele x, der giver en levealder der er større end eller lig med 81,5. Endelig skal dette x lægges til 1995 for at finde årstallet. Man får med hensyn til x:

   0,23·x + 78,0 = 81,5 ⇔

   x = (81,5 - 78,0)/0,23 ⇔

   x = 15,217. Man indsætter x = 15 henholdsvis x = 16 i formlen for at se om man skal runde op aller ned...

   x = 15 giver: 0,23·15 + 78,0 = 81,45

   x = 16 giver: 0,23·16 + 78,0 = 81,68

   Dvs x = 16 er det antal hele år, der går, før man når over en levealder på 81,5. Dvs. denne levealder opnås i år 1995 + 16 = 2011

   (Man kan også argumentere for, at x = 15,2 svarer til et tidspunkt i 2010, og at 2010 dermed er svaret. Spørg evt. lærer eller eksamensvagt.)