Svar på opgave 1:

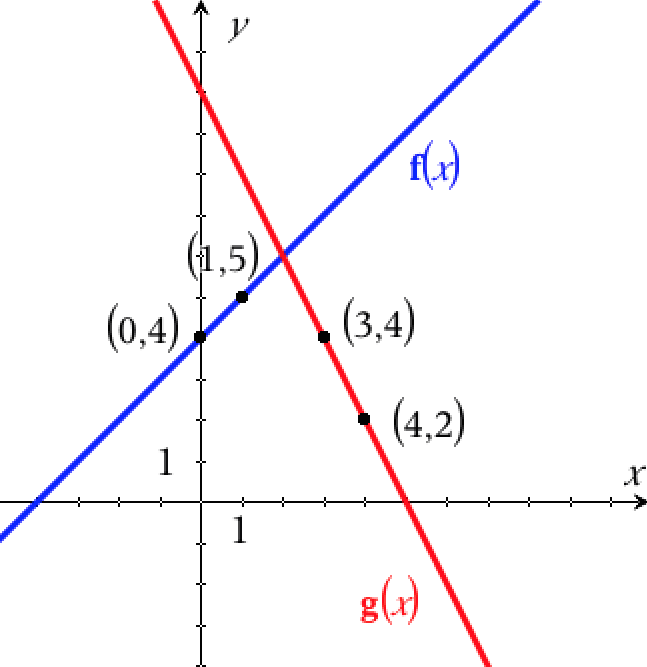
1. Det antages, at g er en lineær funktion selvom det ikke fremgår af opgaven. For at tegne graferne for f og g, så beregner man to punkter på hver linje.

   For f får man punkterne (0,4) og (1,5). For g vælger man (3,4), der er opgivet og (4,2), der beregnes ud fra (3,4) ved at lægge 1 til x og trække 2 fra y, da hældningen er -2.

   Det giver følgende grafer:

   

Svar på opgave 2:

1. Man indsætter s = 5 og L = 8 i formlen og får følgende løsning med hensyn til h:

   5 = h·100/8 ⇔ h = 0,4

   Dvs. højden er 0,4 km = 400 m

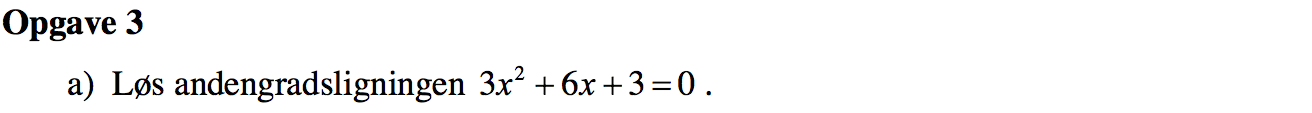
Svar på opgave 3:

1. 3x² + 6x + 3 = 0 ⇔

   x = -6/(2·3) ± [1/(2·3)]·√[36-4·3·3] ⇔

   x = -1 ± (1/6)·√0 ⇔

   x = -1

Svar på opgave 4:

1. Løsningerne til ligningen f(x) = 0 er de x-værdier, hvor grafen til f skærer x-aksen. For x-aksen gælder, at y = 0 og dermed også, at f(x) = 0.

   Man aflæser løsningerne til x = -3 ∨ x = 8 (vist med rødt på figuren nedenunder).

   

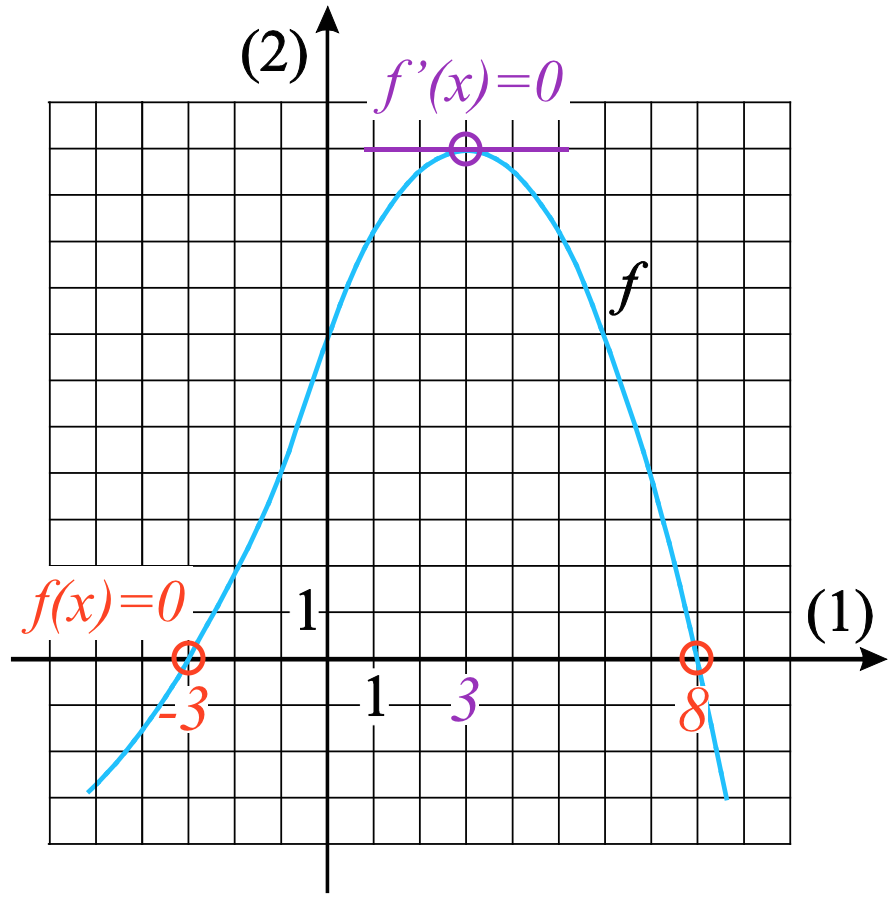
   Løsningerne til f´(x) = 0 er de x-værdier, hvor hældningen til tangenten til f er 0. Af figuren ovenfor ses det at gælde for x = 3 (vist med lilla).

   Dvs. ligningen f(x) = 0 har løsningerne x = -3 eller x = 8

   Ligningen f´(x) = 0 har løsningen x = 3

Svar på opgave 5:

1. Modellen er f(x) = 4770·(1-2%)^x = 4770·0,98^x,

   f(x) er familiernes forbrug i kWh, x er antal år efter 2005, 4770 er antallet af kWh, som familierne bruger i 2005 (x = 0) og 0,98 er fremskrivningsfaktoren, dvs. det tal, som man skal gange sidste års tal med for at finde det nye.

Svar på opgave 6:

1. Funktionen f er en stamfunktion til g, hvis f´(x) = g(x).

   Man får f´(x) = [3x²+ln(x)+3]' = 6x + 1/x

   Da dette er lig med g(x), så gælder, at f er en stamfunktion til g

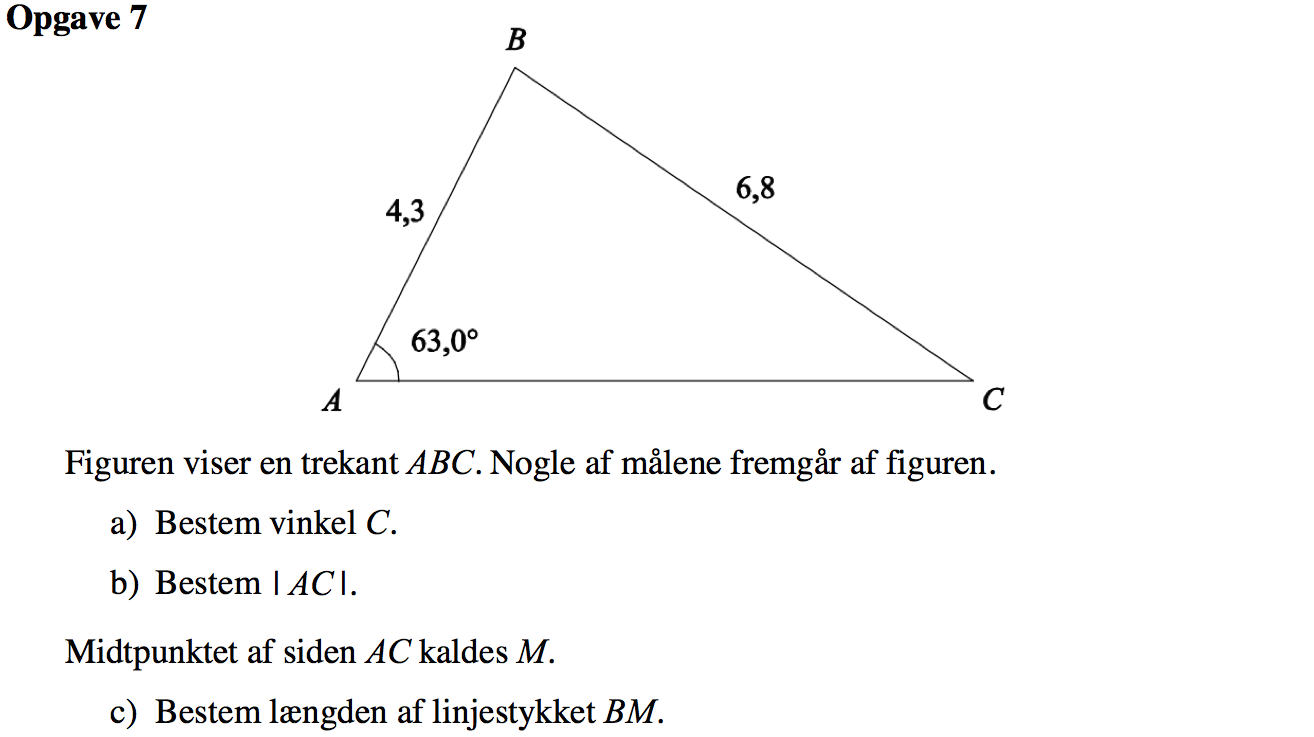
Svar på opgave 7:

1. Vinklen C findes ved hjælp af en sinusrelation.

   solve(sin(63.°)/6.8=sin(c*1.°)/4.3,c)|0<c<90 ▸ c=34.2934

   Dvs. ∠C = 34,2934° = 34,3°

2. Længden |AC| kan findes ved hjælp af en cosinusrelation.

   solve(cos(63.°)=(4.3²+ac²-6.8²)/(2*4.3*ac),ac)|ac>0 ▸ ac=7.57007 (ac er |AC|)

   Dvs. |AC| = 7,57007 = 7,57

3. Midtpunktet af siden AC kaldes M. |AM| = |AC|/2 = 7,57007/2 = 3,78504. BM er vist med rødt på tegningen nedenunder. Nogle fundne værdier af længder og vinkler er skrevet med blåt.

   

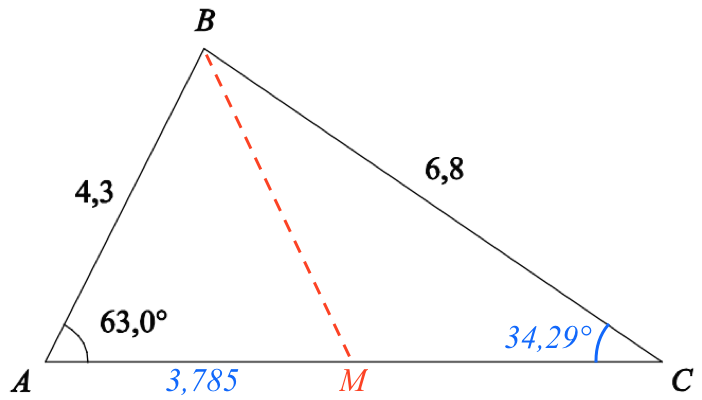
   Længden |BM| findes ved hjælp af en cosinusrelation.

   solve(cos(63.°)=(4.3²+3.78504²-bm²)/(2*4.3*3.78504),bm)|bm>0 ▸ bm=4.24718 (bm er |BM|)

   Dvs. |BM| = 4,24718 = 4,25

Svar på opgave 8:

1. Man starter med at omskrive spørgsmålet til: "Hvad er vægten af hjernen (y) hos et dyr med en vægt (x) på 100 gram?"

   Heraf ses at man skal finde y, når x = 100. Det giver y = 0,0635·100^0,822 = 2,79752.

   Dvs. vægten af hjernen er 2,80 g

   Man kan igen omformulere for at være sikker på, hvad der er x og y. "Hvor meget er vægten af et dyr (x), når vægtens af dets hjerne (y) er mindst 75 gram?"

   Man skal her løse ligningen 75 = 0,0635·x^0,822 med hensyn til x:

   solve(75=0.0635*x^0.822,x) ▸ x=5464.82

   Dvs. dyret skal mindst veje 5465 g

2. Her skal man bruge procent-procent vækst formlen for potensfunktioner: (1 + r_y) = (1 + r_x)^0,822, hvor man skal finde r_y = vækstprocenten for dyrets hjerne og r_x = vækstprocenten for dyrets vægt = 25 %.

   Man får: r_y = ((1 + 25 %)^0.822 - 1)·100 % = (1,25^0.822 - 1)·100 % = 20,1 %

   Dvs. vægten af dyrets hjerne vokser med 20,1 %

Svar på opgave 9:

1. Højden er 35 m, det er det konstante led i andengradspolynomiet.

   Bredden findes ud fra diskriminanten (D) til andengradsligningen -(1/35)x² + 35 = 0. Her er D = (-4)·(-1/35)·35 = 4.

   Der gælder at bredden er lig med afstanden mellem de to løsninger til andengradsligningen. Generelt gælder, at for andengradsligningen ax² + bx + c = 0 er denne afstand lig med 2·(1/2·|a|)·√D = (1/|a|)·√D.

   Her gælder at a = -1/35 og D = 4. Man får derfor bredden: (1/|-1/35|)·√4 m = 35·2 m = 70 m

2. Arealet af en parabel (eller parabelafsnit) er (2/3)·højde·bredde.

   Dette giver her, at arealet er (2/3)·35·70 m² = 1633,3 m²

Svar på opgave 10:

1. f(70) = 2200/(1 + 200·e^{−0,1·(70-25)} agern = 682,8 agern = 683 agern

   Dette er antallet af agern, som et 70-årigt træ producerer.

2. Man skal løse ligningen f(x) = 1000. Man får:

   solve(2200/(1+200*exp(−0.1*(x-25)))=1000,x) ▸ x=76.16

   Dvs. træet skal være 76,2 år gammelt

Svar på opgave 11:

1. distance:={2300,2500,2700,2900,3100,3300,3500,3700} ▸ {2300,2500,2700,2900,3100,3300,3500,3700}

   kondital:={40,45,49,54,58,62,67,71} ▸ {40,45,49,54,58,62,67,71}

   LinRegMx distance,kondital,1: CopyVar stat.RegEqn,f1: stat.results ▸
   [["Titel","Lineær regression (mx+b)"]
   ["RegEqn","m*x+b"]
   ["m",0.022024]
   ["b",−10.3214]
   ["r²",0.999241]
   ["r",0.99962]
   ["Resid","{...}"]]

   Heraf ses at a = 0,0220 og b = 10,32

   (a i opgaven svarer til m i Ti-Nspire).

2. Hans kondital er steget: 450·0,022024 = 9,9

   (Når sammenhængen er y = ax + b, vil en stigning af x på 450 føre til en stigning af y på a·x.)

Svar på opgave 12:

1. Man opretter f(x).

   f(x):=0.25*x⁴-x³+x² ▸ Udført

   Man skal lave en fortegnsundersøgelse af f´(x). Først løser man ligningen f´(x) = 0.

   solve(derivative(f(x),x)=0,x) ▸ x=0. or x=1. or x=2. (f´(x)=0 ⇒ x=0, x=1 eller x=2)

   Man undersøger fortegnet for f´(x) omkring nulpunkterne:

   derivative(f(x),x)|x=−1 ▸ −6.

   derivative(f(x),x)|x=0.5 ▸ 0.375

   derivative(f(x),x)|x=1.5 ▸ −0.375

   derivative(f(x),x)|x=2.5 ▸ 1.875

   Dette viser, at f er aftagende for x < 0, voksende for 0 < x < 1, aftagende for 1 < x < 2 og voksende for x > 2,

2. Tangentens ligning er y = f´(3)·(x - 3) + f(3). Man finder f´(3) og f(3):

   derivative(f(x),x)|x=3 ▸ 6. (f´(3) = 6)

   f(3) ▸ 2.25

   Dette giver følgende ligning for tangenten: y = 6·(x - 3) + 2,25 ⇔ y = 6x - 15,75

   (I Ti-Nspire kan man benytte tangentLine-kommandoen: y=tangentLine(f(x),x,3) ▸ y=6*x-15.75)

3. Man skal løse lignigen f´(x) = 0,375. Man får:

   solve(derivative(f(x),x)=0.375,x) ▸ x=0.348612 or x=0.5 or x=2.15139

   Dvs. første koordinaterne er x = 0,3486, x = 0,500 eller x = 2,151.