Svar på opgave 1: Olivers økonomi

1. Olivers månedsløn i oktober er: 75,35 kr./time · 160 timer = 12.056 kr.
2. Olivers arbejdstid i november er: 12.432,75 kr. : (75,35 kr./time) = 165 timer
3. Udbetalt løn = 12.432,75 kr. · 0,92 - (12.432,75 kr. · 0,92 - 4.673) · 0,38 = 8867,38 kr.
4. Den første rente er 99.000 kr. · 0,006 = 594 kr.
5. Olivers afdrag de første fire måneder er : 1906 kr. + 1917,44 kr. + 1928,94 kr. + 1940,51 kr. = 7692,89 kr.
6. Renten = (samlet ydelse) - lån = (45·2500 kr. + 875,44 kr.) - 99.000,00 kr. = 14.375,44 kr.
7. Faste månedlige udgifter = (890/6) kr. + (4000/6) kr. + 350 kr. + 2500 kr. = 3665 kr.
8. De samlede anslåede udgifter til bilen det første år = (0,6 · 20.000 + 43.980) kr. = 55.980 kr.
9. De samlede årlige udgifter = udgift til benzin + årlige faste udgifter.
   Tallet 0,6 i formlen er udgiften på benzin pr. kørt km, som er: (10,80 kr./L)/(18 km/L) = 0,60 kr./km.
   Tallet 43.980 er de samlede faste årlige udgifter i kr. til bilen: (12 mdr.)·(3665 kr./mdr.) = 43.980 kr.

Svar på opgave 2: Hvor mange arbejder som tømrere?

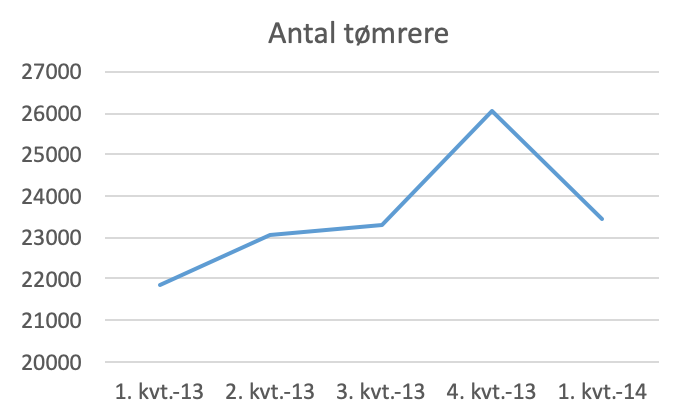
1. Man laver en ekstra kolonne til tabellen med forskellen på antal tømrere. Her finder man den største forskel, 7228, i første kvartal 2014
2. Værdiakserne skærer ikke første-aksen i samme værdi. Den første skærer i 13.500, den anden i 0. Derfor bliver den anden kurve fladere.
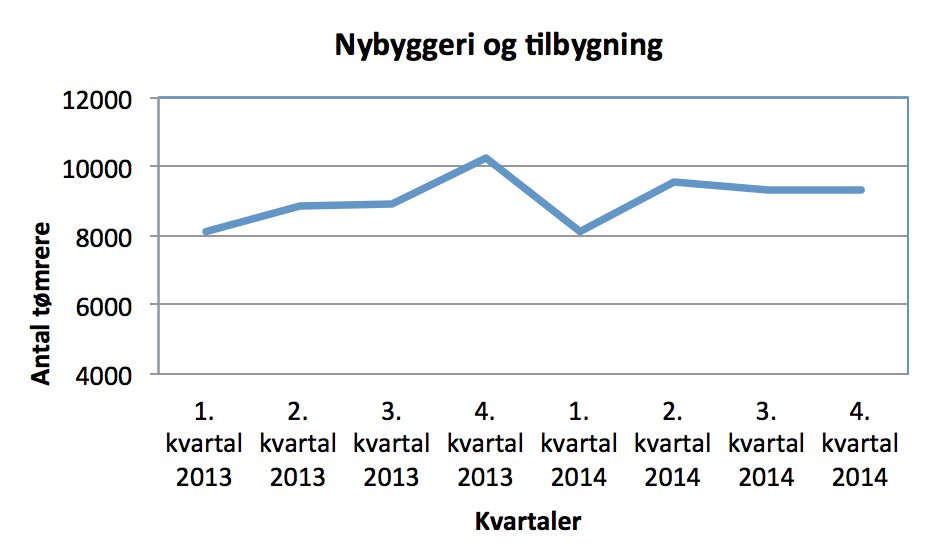
3. Nedenfor er et diagram i Excel over udviklingen i antallet af tømrere inden for nybyggeri og tilbygning fra 1. kvartal 2013 til 4. kvartal 2014.
   
4. Som vist nendenunder, stiger antallet af tømrere mellem 1. og 3. kvartal 2013 fra ca. 22.000 til ca. 26.000. Dette svarer til en stigning på: (26.000 - 22.000)/22.000 = 0,20 = 20 %. Herefter er der et fald fra 26.000 til 23.000 personer i 1. kvartal 2014, der svarer til 3000 personer eller (3000/26.000) = 0,115 ≈ 12 %.
   

Svar på opgave 3: Oliver og Albert bygger trapper

1. Hver trin skal have højden: 900 mm/5 = 180 mm = 18 cm
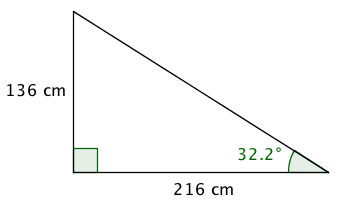
2. Tegningen er lavet i Geogebra. Vinklen ses at være 34,19°, hvilket opfylder kravet.
   
3. Man har at: S = 17 cm og 2·S + G = 61 cm ⇔ 2·17 cm + G = 61 cm ⇔ G = 61 cm - 34 cm = 27 cm
4. S = 136 cm/8 = 17 cm. I følge formlen skal der gælde, at 2·S + G ligger mellem 61 cm og 63 cm. Her vælges 61 cm, og man får: G = (61 - 2·17) cm ⇔ G = 27 cm. Trappens længde er: (antal trin)·G = 8·27 cm = 216 cm. Vinklen på trappen bliver 32,2° som vist på tegningen.
   

Svar på opgave 4: Oliver bygger en terrasse

1. Arealet af terrassegulvet er 4,2 m · 7,1 m = 29,82 m²
2. Afstanden mellem tværbjælkerne vælges til 50 cm. Antallet af tværbjælker sættes til x. Den samlede bredde af tværbjælker er x·5 cm. Der er (x - 1) mellemrum mellem tværbjælkerne. Man får ligningen:
   7,1 m = x·5 cm + (x - 1)·50 cm ⇔
   710 cm + 50 cm = x·55 cm ⇔
   x = 760 cm/55 cm = 14 tværbjælker.
3. For de korte sider får man summen af deres kvadrater til: 1,5² + 2,0² = 2,25 + 4,0 = 6,25. For den længste side får man: 2,5² = 6,25. Pythagoras' læresætning er opfyldt og dermed er trekanten retvinklet
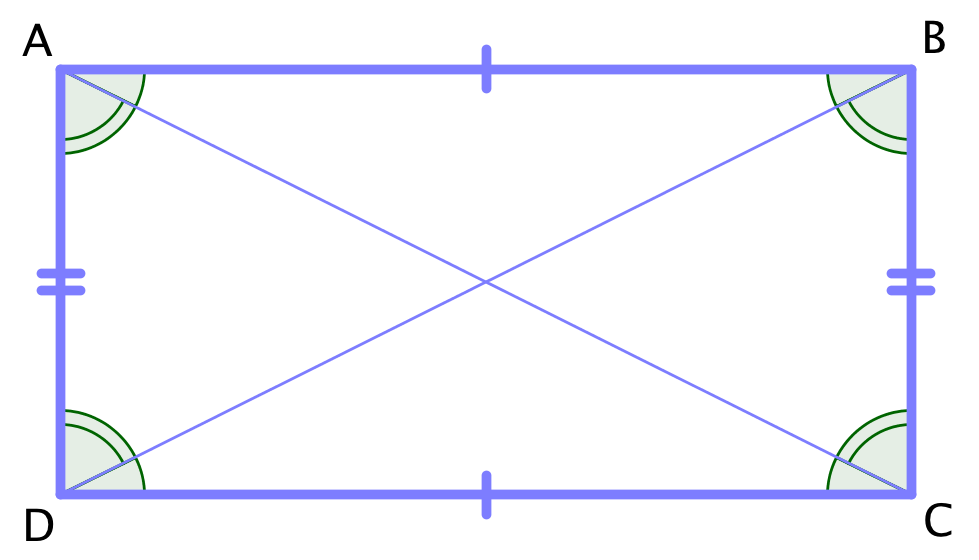
4. På nedenstående tegning har ΔABC, ΔBCD, ΔCDA og ΔDAC ens sider, og de er derfor kongruente. Dermed er firkantens vinkler ens, og den selv et rektangel.
   

Svar på opgave 5: Talkryds

1. Løsning i Geogebra:
   
2. Midtertallet kan være 1, 3 eller 5. De lige tal 2 eller 4 kan ikke bruges, da det vil give en lige sum på den ene led og en lige sum på den anden.
3. (Summen vandret)·2 = (sum af tal) + midtertal, da midtertallet tælles dobbelt. Lægger man tallene fra 1 til 9 sammen og dertil 5, så får man 50. Summen af tallene i den vandrette række er derfor 50/2 = 25
4. Antal tal i den vandrette række kaldes x. Det vil sige, at: 2·x = n + 1 ⇔ x = (n + 1)/2
5. Summen er [97·(97 + 1) + 2·45]/4 = 2399