Svar på opgave 1: Folkeskoler og privatskoler

1. Forskellen på elevtallet i 2005 og 2012 er 8243 - 9412 = -1169. Det vil sige, at der er 1169 færre elever i Hjørring kommune i 2012 end i 2005.
2. Det procentvise fald i antallet af elever er [(9412 - 8243)/9412]·100 % = 12,4 %
3. Man skal tage 12 % af 8243, som giver: 8243·12 % = 989 elever
4. Nedenfor er vist et diagram lavet i Excel, hvor den blå kurve viser udviklingen for folkeskoler og den røde udviklingen for privatskoler.
   
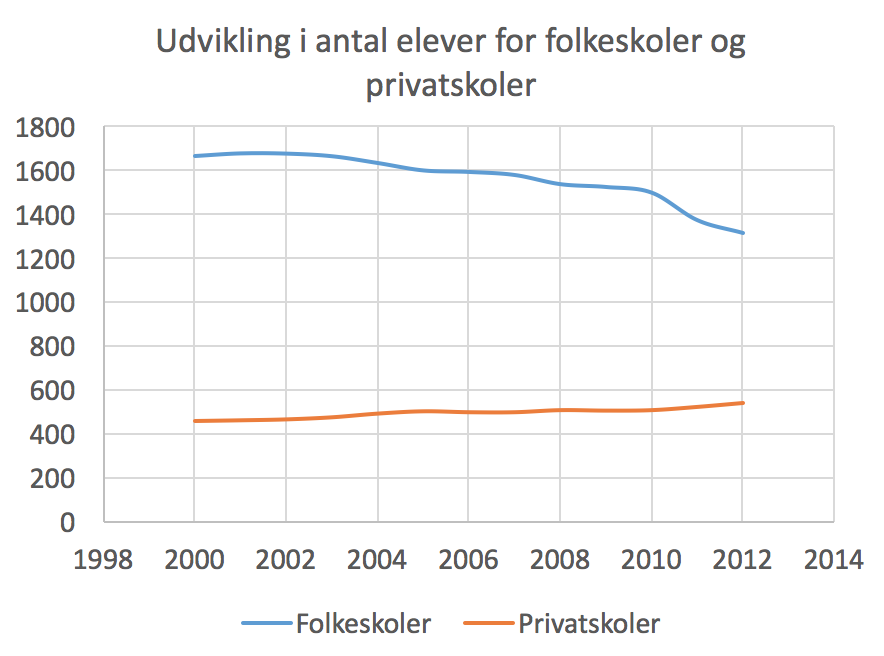
5. Hvis man antager aftagende procentuel udvikling, kan man udregne et gennemsnitlig procentuelt årligt fald ud fra første og sidste værdi for årene 2000 til 2012. Det gennemsnitlige procentuelle fald kaldes x. Man får:
   1318 = 1671·(1 + x)¹² ⇔
   (1318/1671)^1/12 = (1 + x) ⇔
   0,9804 = 1 + x ⇔
   x = −0,0196 = -1,96 %
   Man antager nu samme procentuelle udvikling i yderligere 5 år fra 2012 til 2017. Startværdien for antallet af elever i 2012.
   Antallet af folkeskoler i 2017 bliver: 1318·(1 - 0,0196)⁵ = 1194
6. Man antager en procentuel vækst bare med tallene fra privatskolerne i stedet for folkeskolerne. Man bruger værdien for 2000 som startværdi og skal vise at man med en årlig vækst på 1,3 % får værdien for 2012. Antal år er som forrige spørgsmål lig med 12. Man får:
   459·(1+1,3%)¹² =
   459·1,013¹² =
   459·1,16765 = 536, hvilket skulle vises.

Svar på opgave 2: Undervisningsudgifter

1. Undervisningsudgifterne på svararket er stillet op i nummerorden. Variationsbredden er derfor forskellen mellem det største og det mindste tal som vist nedenunder:
   
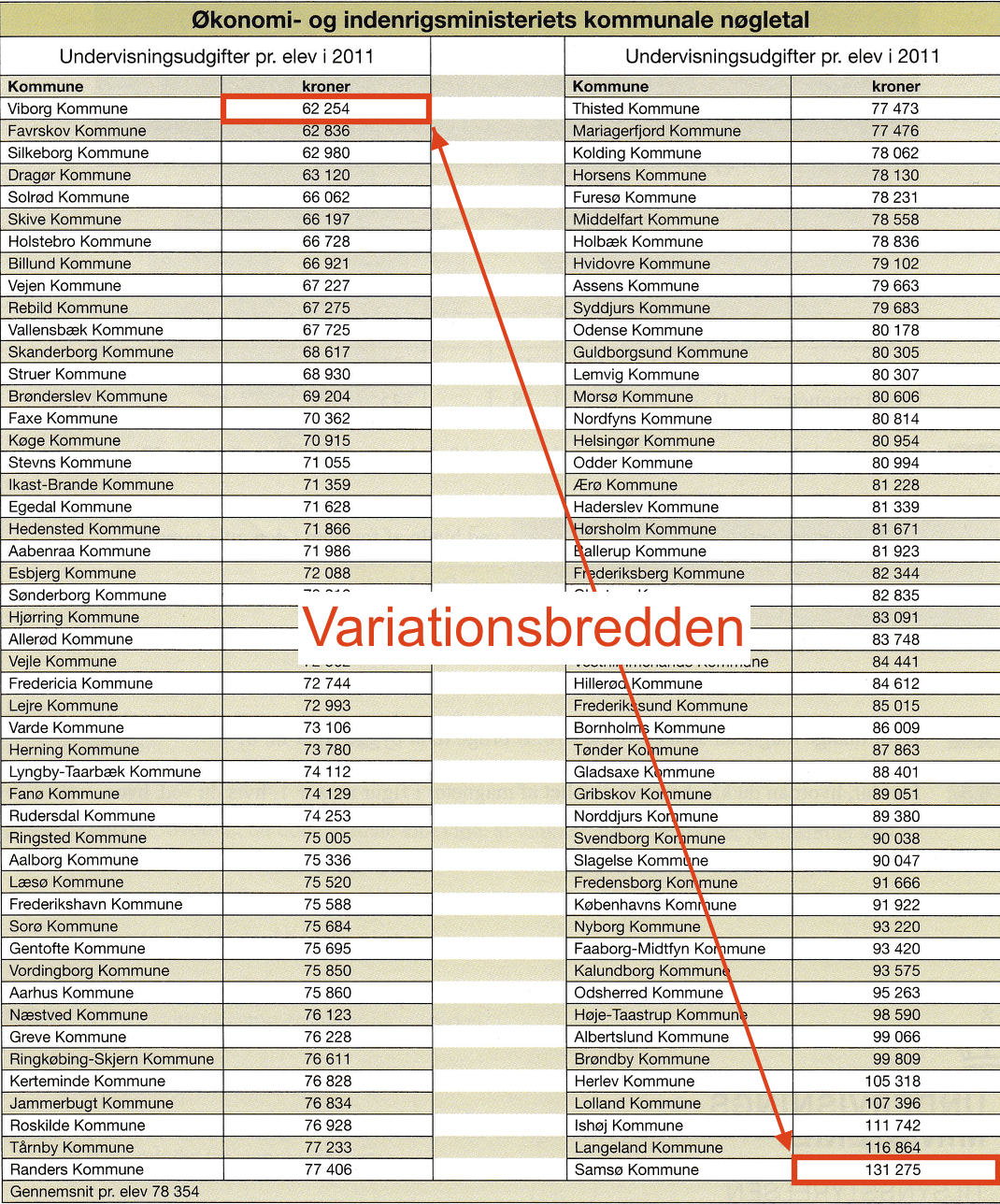
   Det vil sige, at variationsbredden er 131.275 kr. - 62.354 kr. = 69.021 kr.
2. Det bemærkes at der er et lige antal tal. Medianen er derfor gennemsnittet af de to midterste tal som vist nedenunder:
   
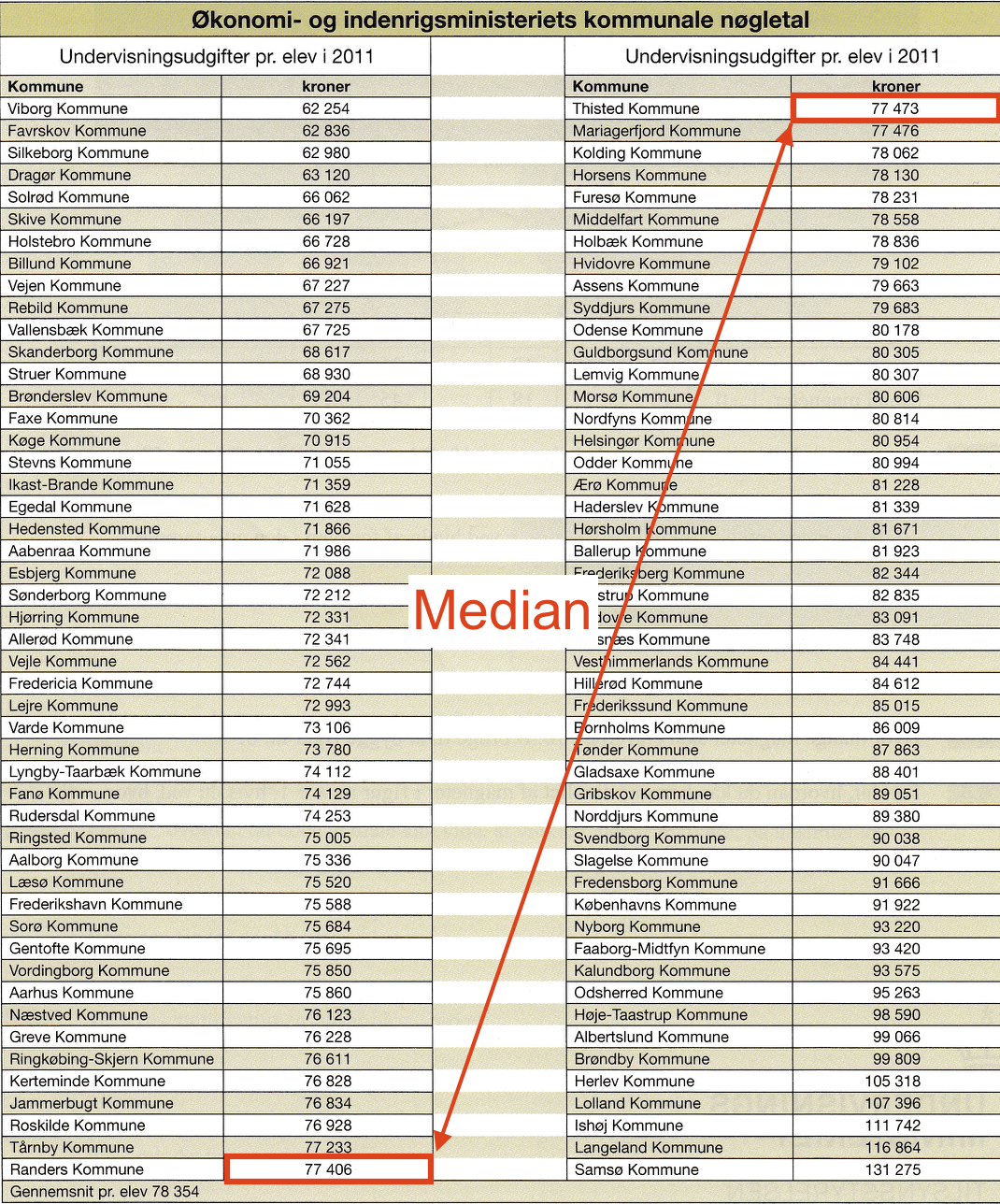
   Det vil sige, at medianen er (77.406 kr. + 77.473 kr.)/2 = 77.439,50 kr.
3. Påstand a: det dobbelte af Viborgs udgifter pr. elev er (62.254 kr.)·2 = 124.508 kr. Da dette er mindre end 131.275 kr. er påstanden rigtig.
   Påstand b: påstanden svarer til påstand a og er dermed rigtig. Man får ved beregning: (131.275 kr.)/2 = 65.637,50 kr. Da dette er større end 62.254 kr., er påstanden rigtig.
   Påstand c: Når 62.254 kr. vokser med 211 % bliver det til: 62.254 kr. + (62.254 kr.)·(211 %) = (62.254 kr.)·(1 + 211 %) = (62.254 kr.)·(1 + 211/100) = (62.254 kr.)·(1 + 2,11) = (62.254 kr.)·3,11 = 193.609,9 kr. Det vil sige, at påstand c er forkert
   Påstand d er rigtig, idet (62.254 kr.)·2,11 = 131.355,94 kr., som ca. er lig med udgiften pr. elev i Samsø kommune.
4. Diagrammet viser et boksplot for henholdsvis 2001 og 2011.
   
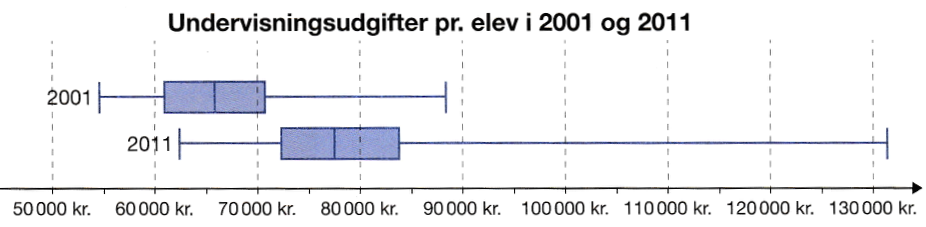
   Fordelingen af udgifter har en større variationsbredde i 2011 end i 2001. Det ses af, at boksplottet for 2011 er bredere end boksplottet for 2011.
   Kvartilsættet for de to fordelinger er de lodrette streger i den midterste firkant i hvert plot.
   Kvartilsættet er nedre kvartil, median og øvre kvartil. Den nedre kvartil for de to fordelinger er 61.000 kr. for 2001 og 72.000 kr. for 2011.
   Medianerne er 65.000 kr. for 2001 og 77.000 kr. for 2011.

Svar på opgave 3: En skoles idrætsområde

1. Hegnets omkreds er 2·(75 m) + 2·(110 m) = 150 m + 220 m = 370 m
2. Banen kan højst være 65 m bred og 100 m lang som vist på tegningen nendenunder:
   
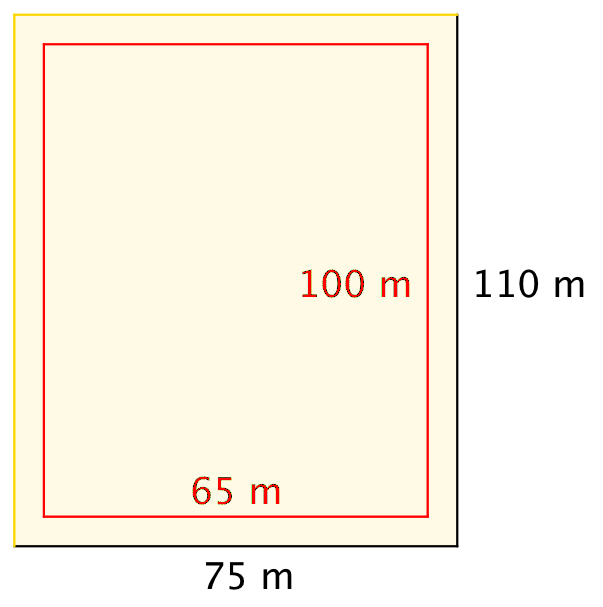
   Den røde firkant, hvor man tager hensyn til det 5 m brede område, er 10 m mindre end den gule firkant på hver led.
3. Nedenfor er tilløbsområdet tegnet og nogle mål skrevet ind:
   
   Man kan måle, at vinklen v for kasteområdet er 29°
4. Nedenfor er vist et forsøg på at passe spydkastområdet ind i den hvide firkant (her vist med brunt).
   
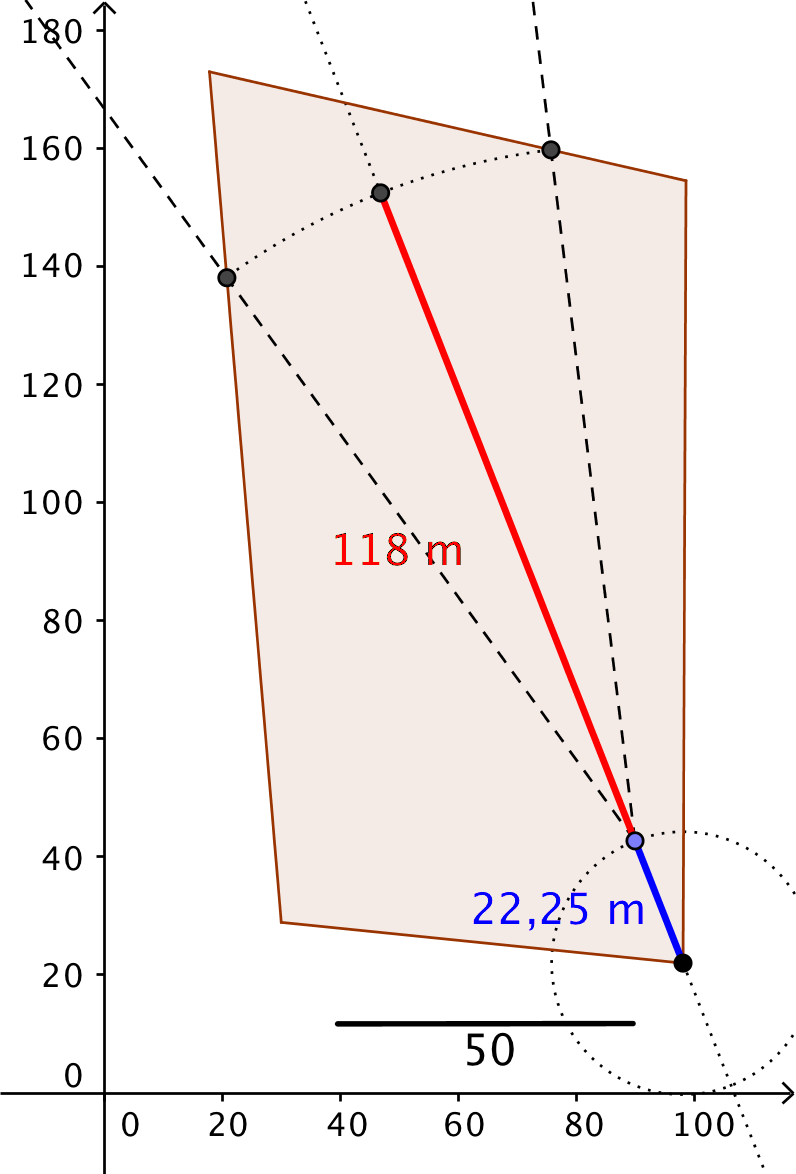
   Den størst mulige længde af spydkastområdet er målt til 22,25 m + 118 m ≈ 140 m

Svar på opgave 4: Et fysikforsøg

1. Den sidste måling er lavet efter 300 sekunder som vist.
   
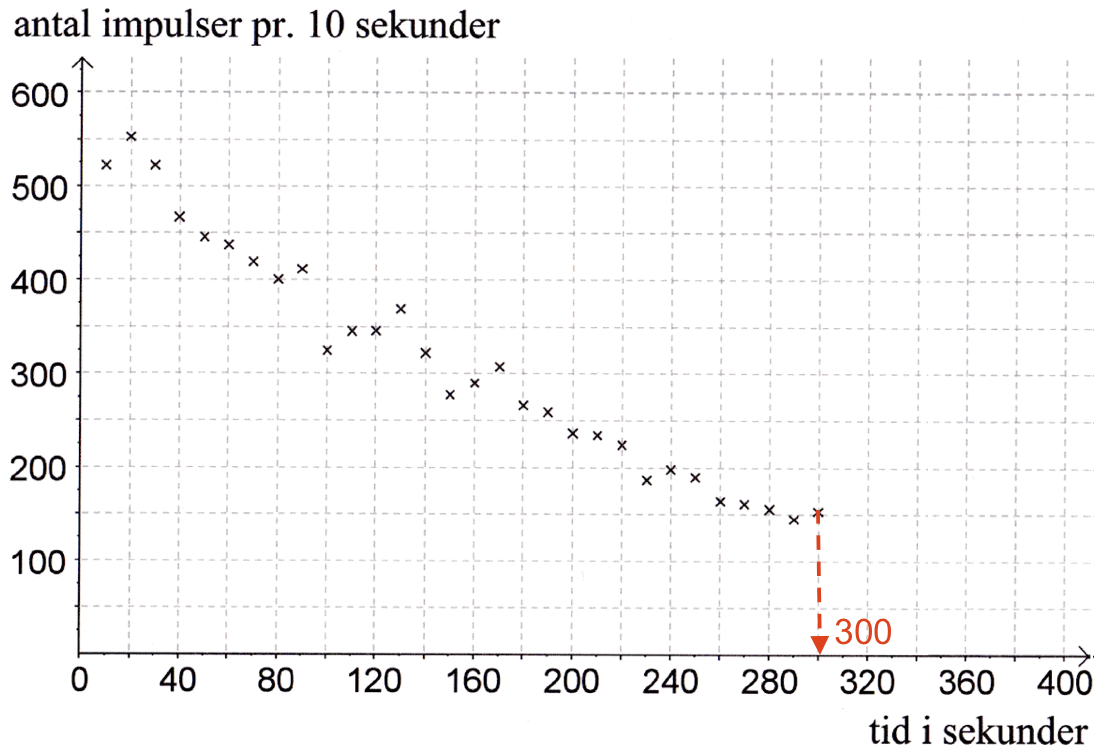
   Det vil sige, at 10. B foretog målinger i 300 s
2. Halveringstiden er den tid det tager at halvere antallet af impulser pr 10 sekunder. Man bestemmer selv, hvor man starter, da halveringstiden er konstant for en eksponentialfunktion. Nedenfor er halveringstiden målt som tiden, der går fra antallet af impulser er 400 pr. 10 sekunder til den er 200 pr. 10 sekunder.
   
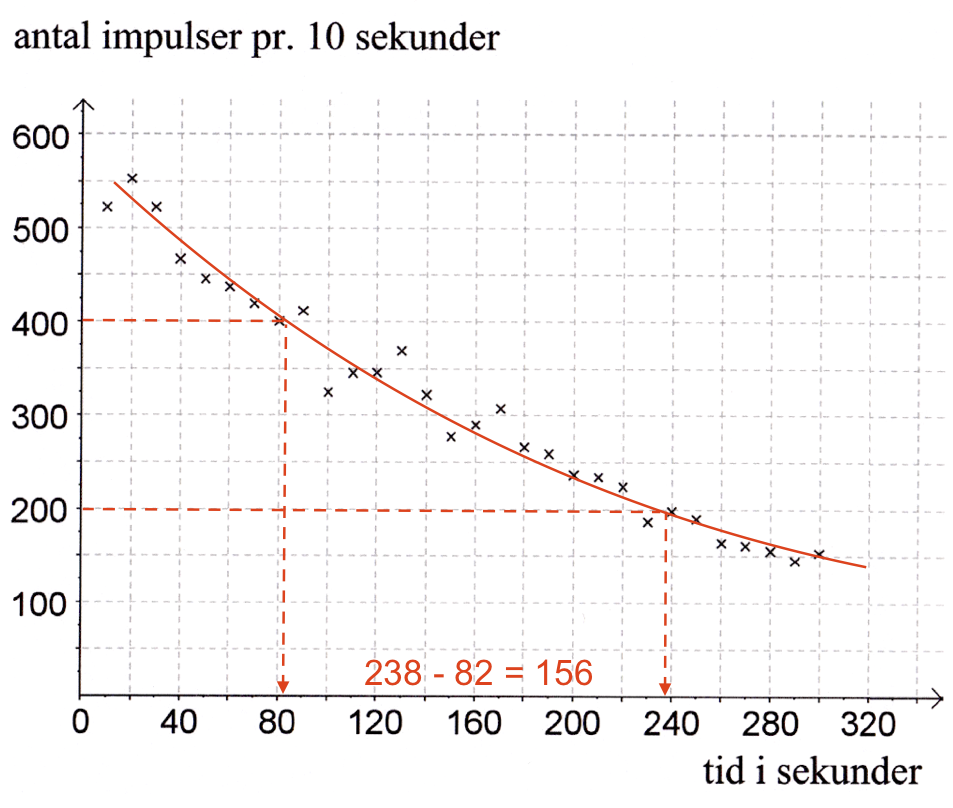
   Dette giver som vist halveringstiden 156 s.
3. Værdien for x = 0 er 586·0,99557⁰ = 586. Dette er startværdien af radioaktiviteten.
   Hvis halveringstiden er 156 s, betyder det at til tiden x = 156 vil denne værdi være halveret. Det vil sige, at værdien til x = 156 s skal være 586/2 = 293 (med enheden: impulser pr. 10 sekunder). Man får:
   586·0,99557¹⁵⁶ = 293,2
   Dette viser, at halveringstiden er 156 s
4. Nedenfor er vist en graf for f(x). Den er lavet i Geogebra.
   
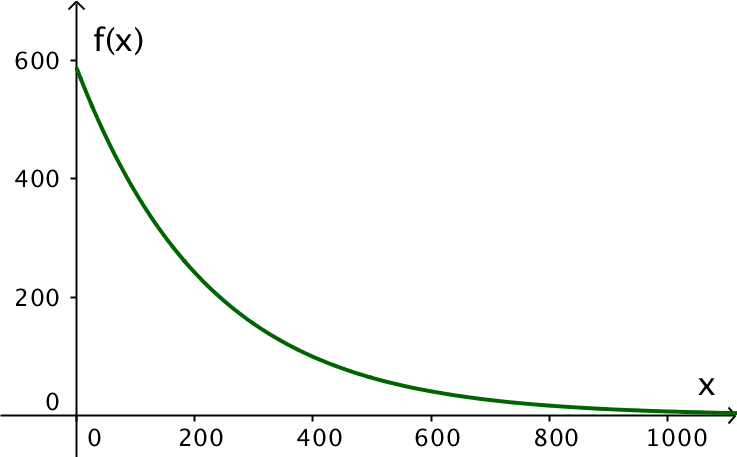
5. Man kan finde tiden ved at forstørre kurven op som vist nedenfor:
   
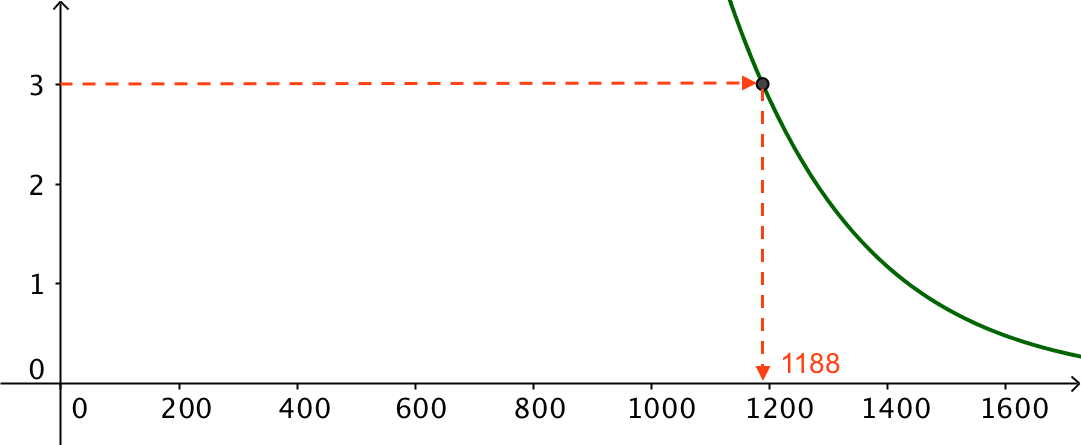
   Man aflæser tiden, hvor barium-137 holder op med at være radioaktivt, til 1188 s

Svar på opgave 5: En rosette

1. Der er tale om en drejning på 45° af den regulære ottekant omkring punktet O. Drejningen er foretaget 7 gange. (Den 8. gang er man tilbage, hvor man startede.)
2. Tegningen nedenunder viser, at vinklen dannes af to regulære ottekanter, som deler en side (markeret med grønt).
   
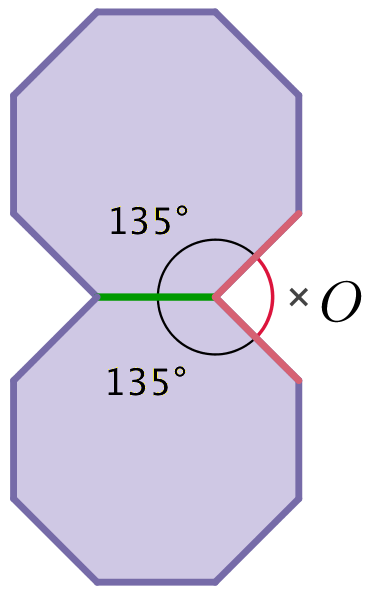
   De to vinkler, der ligger inde i ottekanterne, er begge 135° og tilsammen 270°. Sammen med den røde vinkel skal de give 360°, da de danner en fuld cirkel omkring et punkt.
   Det vil sige, at den røde vinkel er 360° - 270° = 90°
3. Rosetten har 8 symmetriakser, som er vist med hver sin farve på figuren nendenunder:
   
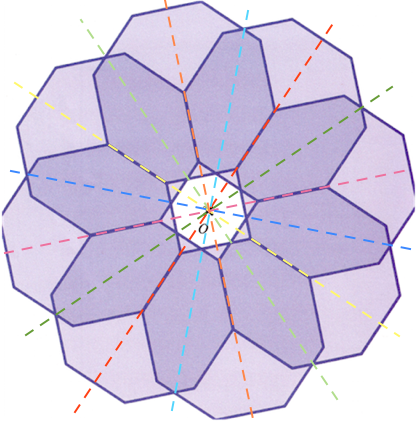
4. Nedenfor er tegnet en regulær femkant drejet 72° fem gange omkring det røde punkt, hvilket giver den viste roset.
   
   Tegningen er lavet i Geogebra.

Svar på opgave 6: Figurer af kugler og magneter

1. Tegning af figur 4 lavet i Geogebra:
   
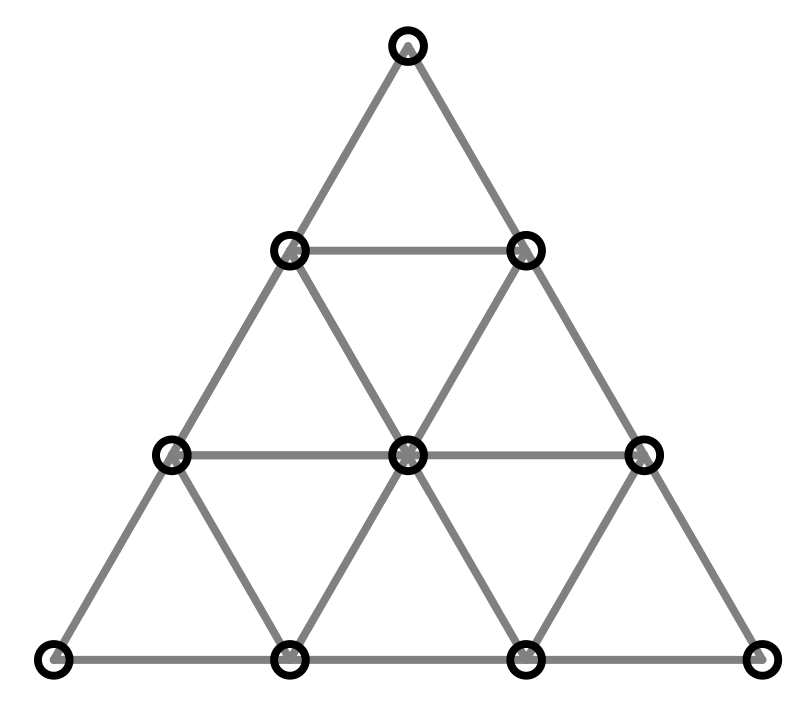
2. Tegning af figur 5 lavet i Geogebra:
   
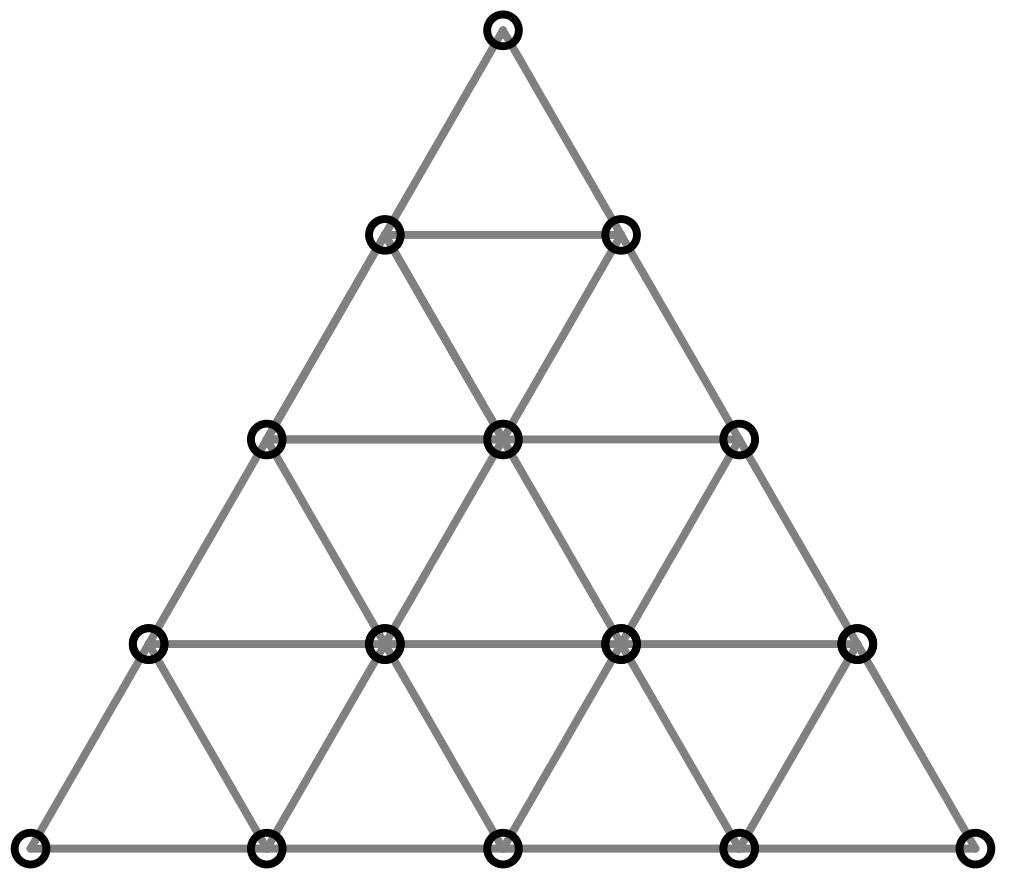
   Det ses, at figuren har 15 kugler og 30 magneter
3. Antal kugler for figur nr. 10 = 10·(10 + 1)/2 = 55
4. Antallet af magneter vokser som tre-tabellen: 3, 6, 9, 12, 15, 18, 21...det vil sige, at man skal lægge 1·3 til antallet af magneter i figur 1 for at få antallet af magneter i figur 2...2·3 til antallet af magneter i figur 2 for at få antallet af magneter i figur 3...osv.
   Derfor skal man lægge 7·3 til 63 for at få antallet af magneter i figur 8, det vil sige, at antallet af magneter i fígur 8 er 21 + 63 = 84
5. Man kalder antallet af magneter i figur n for M(n). Ud fra foregående spørgsmål kan man udlede, at
   M(n+1) = M(n) + 3·n