Svar på opgave 1: Jordvarme

1. Areal = (32 m)·(25 m) = 800 m²
2. Man får at 2,5 gange husets areal er: 2,5·(310 m²) = 775 m². Da dette er mindre end grundens areal på 800 m² er grunden stor nok til et jordvarmeanlæg.
3. En forenklet beregning, der giver en mindre længde af slangen end den rigtige er følgende:
   (antal vindinger af slangen minus den sidste) gange (længde af en vinding, hvor man ikke tager hele buens længde med) =
   (32m/1,25m)·(25m) = 640 m. Dette viser, at slangen er mindst 640 m og derfor større end 580 m. Dermed er der plads til mindst 580 m slange på jordstykket.
4. Man skal beregne rumfanget af slangen. Rumfanget er slangens længde gange dens tværsnitsareal. Man regner i dm for at få et resultat i L (der er dm³). Man får følgende: (5800 dm)·[π·(0,34dm/2)²] = 527 dm³ = 527 L
5. De skal betale følgende beløb for væske til slangen:
   Uden moms: [(527 L)/(20 L/dunk)]·(369,60 kr./dunk) = 9.738,96 kr.
   Med moms: (9.738,96 kr.)·125% = 12.174 kr.

Svar på opgave 2: Solenergi

1. Forskellen mellem dyreste tilbud (ABC-energi) og billigste tilbud (FK-energi) er: 10.389,75 kr. - 9.409,50 kr. = 980,25 kr.
2. Den procentvise forskel på Vindenergi's tilbud på 10.115 kr. og FK-energi's tilbud på 9.409,50 kr. beregnes på følgende måde:
   [(10.115 - 9.409,50)/9.409,5]·100% = 7 %
3. Nedenunder er der i Excel vist en beregning af den samlede pris for et årligt forbrug på 4500 kWt i ti år med en årlig prisstigning pr. kWt på 4%.
   
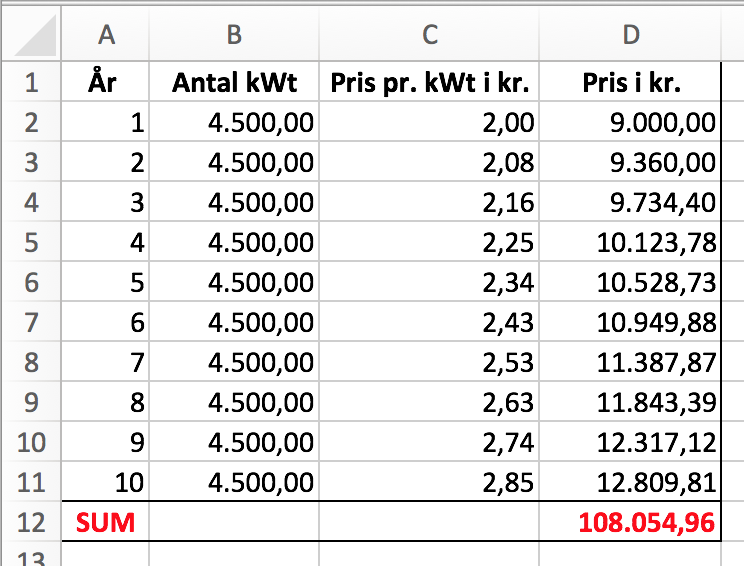
   Den samlede pris for 10 års normalt elforbrug er 108.055 kr., og dermed svarer 10 års elforbrug omtrent til udgiften til et solcelleanlæg.
4. Etableringsomkostningerne er (40.000 kr.)·2% = 800 kr. Til dette lægger man gebyret på 600 kr. og får samlet 1.400 kr. i udgifter til lånet. Trækker man dette fra det lånte beløb får man (40.000 - 1.400) kr. = 38.600 kr.
5. Beregnngerne i Excel er vist nedenunder. Man forsætter indtil saldoen bliver 0 eller negativ. Det år, den bliver negativ, er lånet betalt.
   Det ses, at saldoen bliver negativ efter 11 år. Derfor tager det 11 år at betale lånet.
   
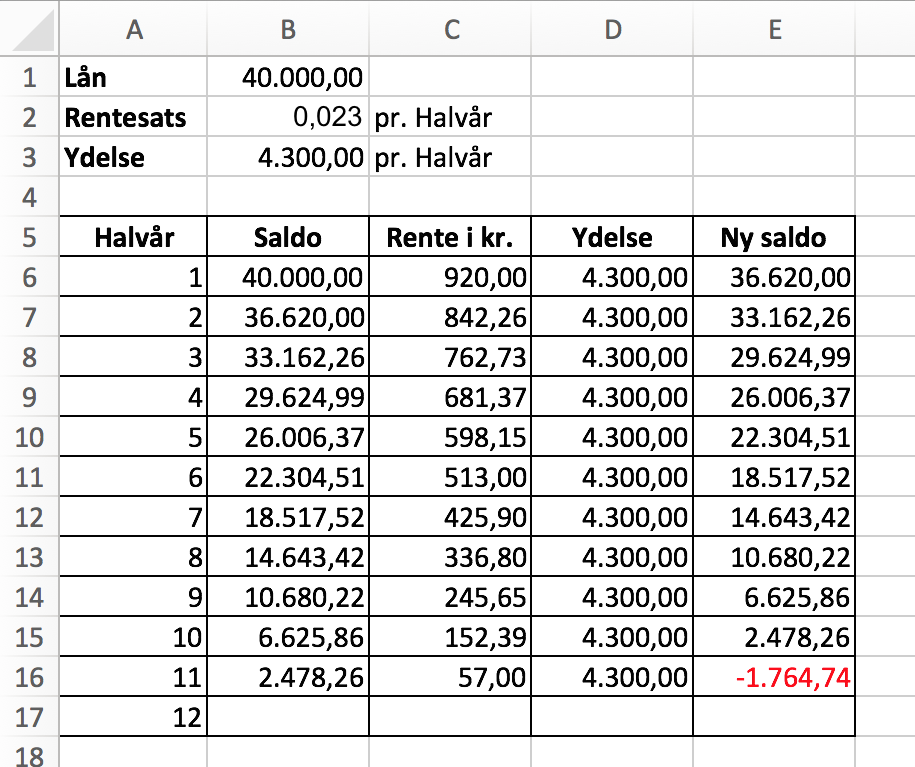
   Følgende formler er brugt: Saldo (første år): =$B$1, Rente i kr: =B6*$B$2, Ydelse: =$B$3, Ny Saldo: =B6+C6-D6 og Saldo (øvrige år): E6
6. Nedenfor er tallene indtegnet i et X-Y punktdiagram i Excel.
   
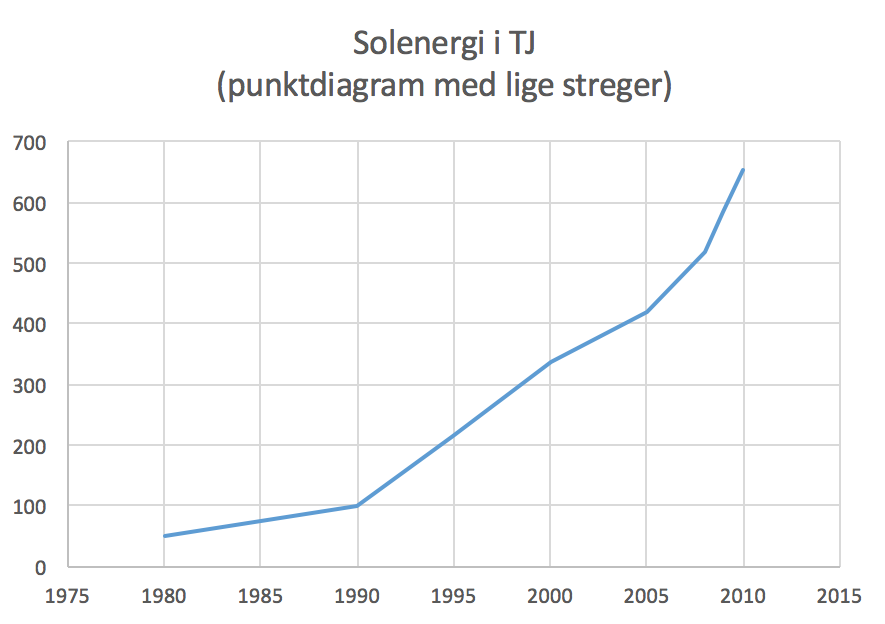
7. Nedenfor er vist samme Excel-diagram som i opgave 6, men med eksponentiel tendenslinje, som er fremskrevet med 5 år (punkteret kurve). Med denne tendenslinje kan værdien i 2015 forudses til at være 1020 TJ
   
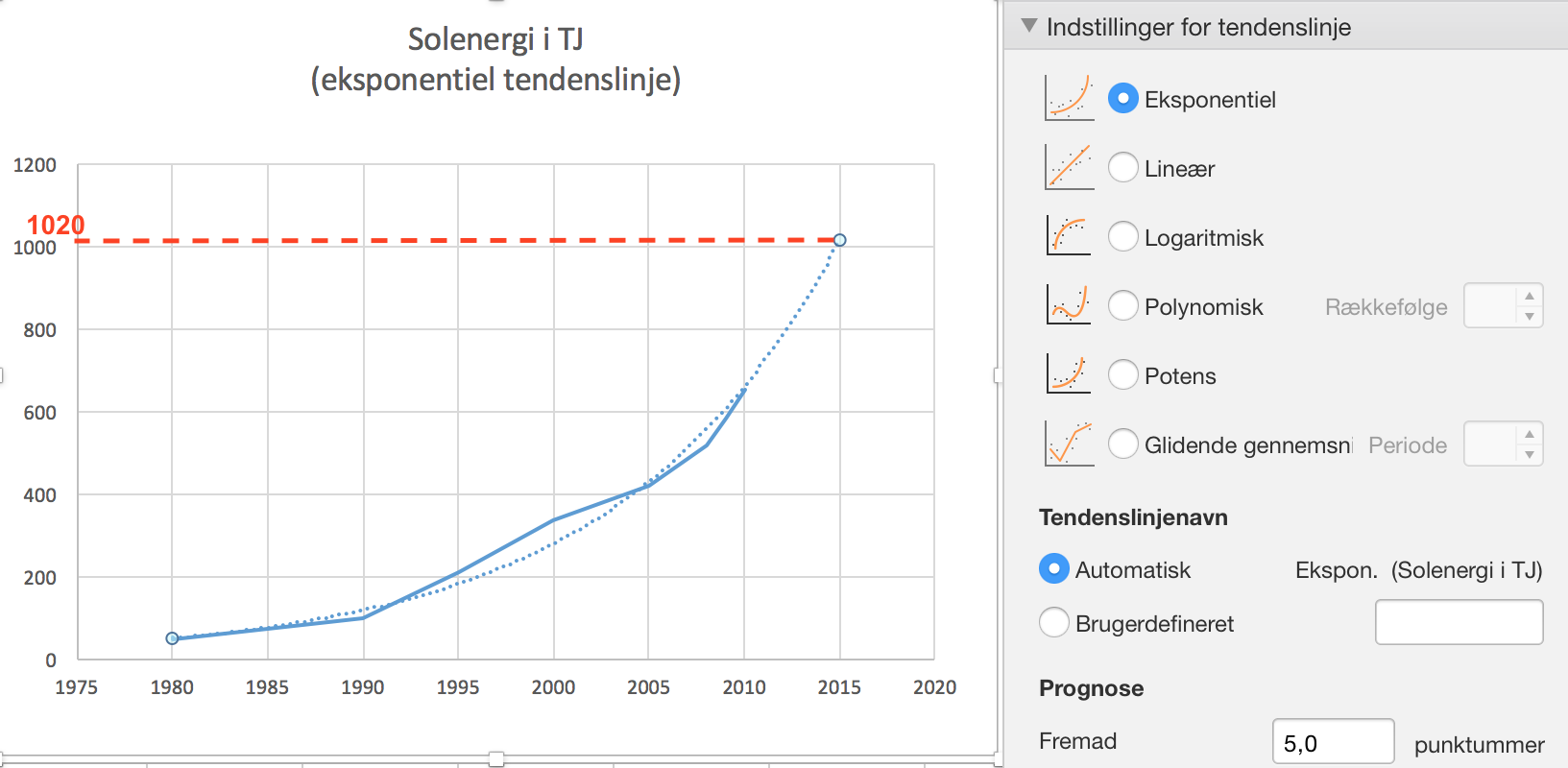
8. Energiforbruget for en familie i 2010 er målt i Joule: (26.500 kWt)·3,6·10⁶J = 9,54·10¹⁰ J.
   Dette omregnes til Tera Joule: 9,54·10¹⁰ J = (9,54·10¹⁰ J)·(T/10¹²) = 9,54·10^-2 TJ.
   Energiforbruget for en familie i 2010 divideres op i den samlede energiproduktion på 653 TJ. Derved får man antallet af familier, der kunne få deres energibehov dækket af solenergi, det år:
   (653 TJ)/(9,54·10^-2 TJ/familie) = (653/9,54)·10² familier = (653/9,54)·100 familier = 6.845 familier

Svar på opgave 3: Elpærer

1. Pæren holder i 2 år ved en brændetid på 2,7 timer pr. døgn. Det svarer til (2 år)·(365 dage/år)·(2,7 timer/dag) = 1971 timer
2. Medianen af tallene i Excel-tabellen findes til 1975 ved hjælp af kommandoen =MEDIAN().
3. Det, som man kan aflæse af boksplottet, er som vist: Mindsteværdien, medianen og størsteværdien samt 1. og 3. kvartil.
   
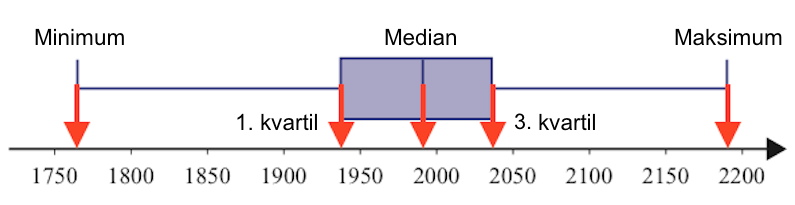
   Mindsteværdien aflæses til 1770 timer, medianen aflæses til 1985 timer og størsteværdien aflæses til 2185 timer
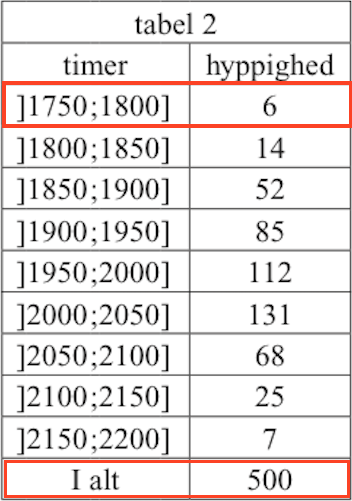
4. Sandsynligheden for at pærens levetid højst er 1800 timer aflæses i tabellen til 6/500 = 0,012. Det følger af, at 6 pærer ud af 500 har en levetid mellem 1750 timer og 1800 timer, hvor 1750 timer den mindste levetid, der fundet i undersøgelsen. Aflæsningen i tabellen er vist nedenunder.
   
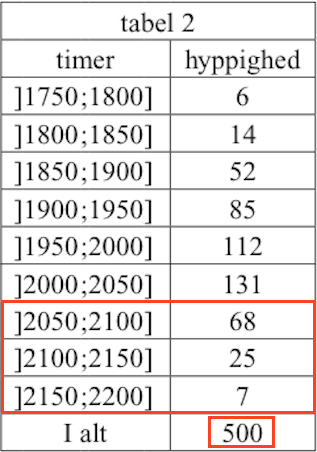
5. Sandsynligheden for at pærens levetid mindste er 2050 timer aflæses som vist nedenunder. Den samlede hyppighed af pærer, som holdt i mere end 2050 timer, er 7 + 25 + 68 = 100. Dette divideres med det samlede antal pærer, og man får 100/500 = 0,20, som er sandsynligheden for at én pære holder i mindst 2050 timer. Sandsynligheden for at begge pærer i en pakke holder mere end 2050 timer er dermed 0,20·0,20 = 0,04.
   

Svar på opgave 4: Vindmøller

1. Det bestrøgne areal er π·(diameter/2)² = π·(120m/2)² = 11310 m²
2. Effekten P = (0,6·8³·11310)/10⁶ MW = 3,47 MW
3. Den største effekt aflæses som værdien på y-aksen ud for den vandrette øverste linje. Værdien er ca. 3,6 MW
4. Den røde kurve fortæller, at når vindhastigheden er mellem 0 og 4 m/s udvikler møllen ingen elektrisk effekt. Mellem 4m/s og 12 m/s stiger effekten.
   Med en vindhastighed mellem 12 m/s og 25 m/s udvikler møllen sin maksimale effekt. Når vindhastigheden kommer over 25 m/s stopper møllen og udvikler ingen effekt.
5. Den procentdel af vindens effekt der kan omdannes til elektrisk effekt af møllen beregnes ved formlen:
   (møllens effekt/vindens effekt)·100% = (1,5 MW/4,95 MW)·100% = 30 %

Svar på opgave 5: Papirfoldning

1. Tegningen skal forstås sådan, at nederste venstre hjørne foldes til midtpunktet af øverste side. Derfor er a halvdelen af 24 cm = 12 cm
2. Man skal vise at b=9 er løsning til ligningen (24 - b)² = b² + 12². Dette gøres ved at dele ligningen i en højreside og en venstreside og se om de to sider giver det samme, når b=9 indsætte i hver af dem. Man får:
   Venstre side: (24 - b)² = (24 - 9)² = 15² = 225
   Højre side: b² + 12² = 9² + 12² = 81 + 144 = 225
   Da venstre side = højre side er b=9 en løsning til ligningen.
3. Tegningen nedenunder viser trekant 1 og trekant 2. Det bemærkes, at begge trekanter har en ret vinkel, og at summen af vinklerne i en trekant er 180°. Desuden gælder, at en vinkel, hvis ben danner en ret linje, er 180°.
   
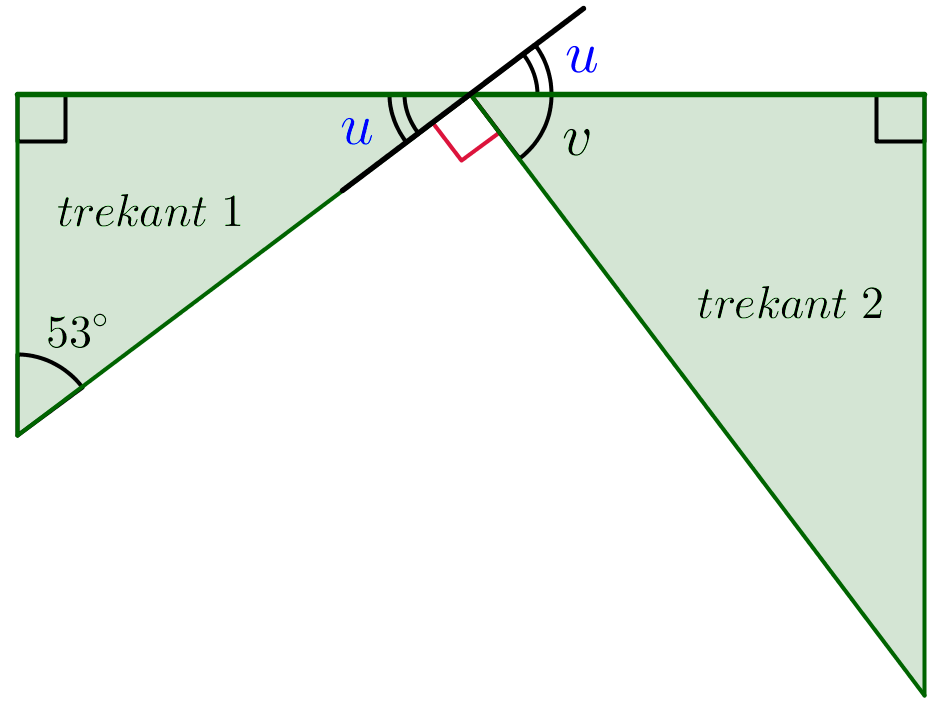
   Ved at forlænge den den ene side i trekant 1, får man et kryds med to ens vinkler kaldet u. Da u indgår i trekant 1 får man, at u = 180° - 90° - 53° = 37°
   Da den røde rette vinkel sammen med v og u giver en ret linje gælder, at 90° + v + u = 180°. Det vil sige, at v = 90° - u = 90° - 37° = 53°.
   Den sidste vinkel i trekant 2 bliver så 180° - 90° - v = 90° - 53° = 37°. Dermed indeholder begge trekanter vinklerne 37°, 53° og 90°.
4. Længden af siden e kan findes ved reglen om, at to ensvinklede trekanter er proportionale. Skaleringsfaktorern mellem trekant 1 og trekant 2 er e/a = d/b = 12/9 = 4/3. Da a = 12 cm får man e = 12cm·(4/3) = 16 cm
5. Som skaleringsfaktor bruger man forholdet e/a.
   1) d = b·(e/a) = (24/50)·(2/6)/(1/5) = 4/5
   2) d = b·(e/a) = (35/72)·(2/7)/(1/6) = 5/6
6. f = c·(e/a) = (17/32)·(2/5)/(1/4) = 17/20